JAC Class 9 Maths Important Questions Chapter 2 Polynomials

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 2 Polynomials Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 2 Polynomials

Question 1.
Find the value of:
(i) 36x² + 49y² + 84xy, when x = 3, y = 6
(ii) 25x² + 16y² – 40xy, when x = 6, y = 7
Solution :
(i) 36x² + 49y² + 84xy
= (6x)² + (7y)² + 2 × (6x) × (7y)
= (6x + 7y)²
= (6 × 3 + 7 × 6)² [When x = 3, y = 6]
= (18 + 42)² = (60)² = 3600

(ii) 25x² + 16y² – 40xy
= (5x)² + (4y)² – 2 × (5x) × (4y)
= (5x – 4y)²
= (5 × 6 – 4 × 7)² [When x = 6, y = 7]
= (30 – 28)² = 2² = 4

Question 2.
If x² + \(\frac{1}{x^2}\) = 23, find the value of (x + \(\frac {1}{x}\)), where x > 0
Solution :
x² + \(\frac{1}{x^2}\) = 23 …. (i)
⇒ x² + \(\frac{1}{x^2}\) + 2 = 25
[Adding 2 on both sides of (i)]
⇒ (x²) + (\(\frac {1}{x}\))² + 2 × x × \(\frac {1}{x}\) = 25
⇒ (x + \(\frac {1}{x}\))² = (5)²
⇒ x + \(\frac {1}{x}\) = 5 (∵ x > 0)

Question 3.
Prove that a² + b² + c² – ab – bc – ca = \(\frac {1}{2}\) [(a – b)² + (b – c)² + (c – a)²].
Solution :
Here, L.H.S. = a² + b² + c² – ab – bc – ca
= \(\frac {1}{2}\) [2a² + 2b² + 2c² – 2ab – 2bc – 2ca]
= \(\frac {1}{2}\) [(a² – 2ab + b²) + (b² – 2bc + c²) + (c² – 2ca + a²)]
= \(\frac {1}{2}\) [(a² – 2ab + b²) + (b² – 2bc + c²) + (c² – 2ca + a²)]
= \(\frac {1}{2}\) [(a – b)² + (b – c)² + (c – a)²]
= R.H.S
Hence, proved.

Question 4.
Evaluate :
(i) (107)²
(ii) (94)²
(iii) (0.99)²
Solution :
(i) (107)² = (100 + 7)²
= (100)² + (7)² + 2 × 100 × 7
= 10000 + 49 + 1400 = 11449

(ii) (94)²
= (100 – 6)² = (100)² + (6)² – 2 × 100 × 6
= 10000 + 36 – 1200 = 8836

(iii) (0.99)²
= (1 – 0.01)² = (1)² + (0.01)² – 2 × 1 × 0.01
= 1 + 0.0001 -0.02 = 0.9801

NOTE: We may extend the formula for squaring a binomial to the squaring of a trinomial as given below. (a + b + c) = (a + (b + c)]² = a² + (b + c)² + 2 × a × (b + c)
[Using the identity for the square of binomial]
= a² + b² + c² + 2bc + 2a (b + c)
[Using (b + c)² = b² + c² + 2bc]
= a² + b² + d² + 2bc + 2ab + 2ac
[Using the distributive law]
= a² + b² + c² + 2ab + 2bc + 2ac
∴ (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac

Question 5.
Simplify : (3x + 4)³ – (3x – 4)³.
Solution :
We have
(3x + 4)³ – (3x – 4)³ = [(3x)³ + (4)³ + 3 × 3x × 4 × (3x + 4)] – [(3x)³ – (4)³ – 3 × 3x × 4 × (3x – 4)]
= [27x³ + 64 + 36x (3x + 4)] – [27x³ – 64 – 36x (3x – 4)]
= [27x³ + 64 + 108x² + 144x] – [27x³ – 64 – 108x² + 144x]
= 27x³ + 64 + 108x² + 144x – 27x³ + 64 + 108x² – 144x
= 128 + 216x²
∴ (3x + 4)³ – (3x – 4)³ = 128 + 216x²

Question 6.
Evaluate:
(i) (1005)³
(ii) (997)³
Solution :
(i) (1005)³ = (1000 + 5)³
= (1000)³ + (5)³ + 3 × 1000 × 5 × (1000 + 5)
= 1000000000 + 125 + 15000 × (1000 + 5)
= 1000000000 + 125 + 15000000 + 75000
= 1015075125

(ii) (997)³ = (1000 – 3)³
= (1000)³ – (3)³ – 3 × 1000 × 3 × (1000 – 3)
= 1000000000 – 27 – 9000 × (1000 – 3)
= 1000000000 – 27 – 9000000 + 27000
= 991026973

Question 7.
If x – \(\frac {1}{x}\) = 5, find the value of x³ – \(\frac{1}{\mathrm{x}^3}\).
Solution :
We have, x – \(\frac {1}{x}\) = 5 ……….(i)
(x – \(\frac {1}{x}\))³ = (5)³
[Cubing both sides of (i)]

Question 8.
Find the products of the following expressions :
(i) (4x + 3y) (16x² – 12xy + 9y²)
(ii) (5x – 2y) (25x² + 10xy + 4y²)
Solution :
(i) (4x + 3y) (16x² – 12xy + 9y²)
= (4x + 3y) [(4x)² – (4x) × (3y) + (3y)²]
We know that (a + b) (a² – ab + b²)
= a³ + b³ [Where a = 4x, b = 3y]
= (4x)³ + (3y)³ = 64x³ + 27y³

(ii) (5x – 2y) (25x² + 10xy + 4y²)
= (5x – 2y) [(5x)² + (5x) × (2y) + (2y)²]
We know that (a – b)(a² + ab + b²)
= a³ – b³ [Where a = 5x, b = 2y]
= (5x)³ – (2y)³ = 125x³ – 8y³

Question 9.
Simplify:
\(\frac{\left(a^2-b^2\right)^3+\left(b^2-c^2\right)^3+\left(c^2-a^2\right)^3}{(a-b)^3+(b-c)^3+(c-a)^3}\)
Solution :
Here (a² – b²) + (b² – c²) + (c² – a²) = 0
∴ (a² – b²)³ + (b² – c²)³ + (c² – a²)³
= 3(a² – b²)(b² – c²) (c² – a²)
= 3(a – b)(a + b)(b – c)(b + c) (c – a) (c + a)
Also, (a – b) + (b – c) + (c – a) = 0
∴ (a – b)³ + (b – c)³ + (c – a)³
= 3(a – b)(b – c)(c – a)
∴ Given expression
= \(\frac{3(a-b)(a+b)(b-c)(b+c)(c-a)(c-b)}{3(a-b)(b-c)(c-b)}\)
= (a + b)(b + c)(c + a)

Question 10.
Prove that : (x – y)³ + (y – z)³ + (z – x)³ = 3(x – y) (y – z) (z – x).
Solution :
Let (x – y) = a, (y – z) = b and (z – x) = c.
Then, a + b + c
= (x – y) + (y – z) + (z – x) = 0
∴ a³ + b³ + c³ = 3abc
Or (x – y)³ + (y – z)³ + (z – x)³
= 3(x – y) (y – z) (z – x)

Question 11.
Find the value of (28)³ + (-78)³ + (50)³
Solution :
Let a = 28, b = – 78, c = 50
Then, a + b + c = 28 – 78 + 50 = 0
∴ a³ + b³ + c³ = 3abc
So, (28)³ + (-78)³ + (50)³ = 3 × 28 × (-78) × 50
= – 327600

Question 12.
If a + b + c = 9 and ab + bc + ac = 26, find the value of a³ + b³ + c³ – 3abc.
Solution :
We have a + b + c = 9 ……(i)
⇒ (a + b + c)² = 81
[On squaring both sides of (i)]
⇒ a² + b² + c² + 2(ab + bc + ac) = 81
⇒ a² + b² + c² + 2 × 26 = 81
[∵ ab + bc + ac = 26]
⇒ a² + b² + c² = (81 – 52)
⇒ a² + b² + c² = 29
Now, we have
a³ + b³ + c³ – 3abc
= (a + b + c)(a² + b² + c² – ab – bc – ac)
= (a + b + c)[(a² + b² + c²) – (ab + bc + ac)]
= 9 × [(29 – 26)] = (9 × 3) = 27

Question 13.
Find the following products:
(i) (x + 2) (x + 3)
(ii) (x + 7) (x – 2)
(iii) (y – 4) (y – 3)
(iv) (y – 7) (y + 3)
(v) (2x – 3) (2x + 5)
(vi) (3x + 4) (3x – 5)
Solution :
Using the identity: (x + a) (x + b)
= x² + (a + b) x + ab, we have
(i) (x + 2)(x + 3) = x² + (2 + 3) x + 2 × 3
= x² + 5x + 6,

(ii) (x + 7)(x – 2) = (x + 7)(x + (-2))
= x² + {7 + (-2)} x + 7 × (-2)
= x² + 5x – 14.

(iii) (y – 4) (y – 3) = {y + (-4)} {y + (-3)
= y² + {(-4) + (-3)} y + (-4) × (-3)
= y² – 7y + 12

(iv) (y – 7)(y + 3) = {y + (-7)} (y + 3)
= y² +{(-7) + 3} y + (-7) × 3
= y² – 4y – 21

(v) (2x – 3) (2x + 5)
= (y – 3) (y + 5), where y = 2x
= {y + (-3)} (y + 5)
= y² + {(-3) + 5} y + (-3) × 5
= y² + 2y – 15
= (2x)² + 2 × 2x – 15
= 4x² + 4x – 15.

(vi) (3x + 4) (3x – 5)
= (y + 4) (y – 5), where y = 3x
= (y + 4) {y + (-5)}
= y² + {4 + (-5)} y + 4 × (-5)
= y² – y – 20 = (3x)² – 3x – 20
= 9x² – 3x – 20

Question 14.
Evaluate:
(i) 35 × 37
(ii) 103 × 96
Solution :
(i) 35 × 37 = (40 – 5) (40 – 3)
= (40 + (-5)) (40+ (-3))
= 40² + (- 5 – 3) × 40 + (- 5 × – 3)
= 1600 – 320 + 15
= 1615 – 320
= 1295

(ii) 103 × 96 = (100 + 3) [100 + (-4)]
= 100² + (3 + (-4)) × 100 + (3 × – 4)
= 10000 – 100 – 12
= 9888

Question 15.
Factorise : 81a²b²c² + 64a²b² – 144a²b²c
Solution :
81a²b²c² + 64a⁶b² – 144a²b²c
= [9abc]² – 2 [9abc][8a³b] + [8a³b]²
= [9abc – 8a³b]² = a²b² [9c – 8a²]²
= a²b²(9c – 8a²) (9c – 8a²)

Question 16.
Factorise :
(3a – \(\frac {1}{b}\))² – 6(3a – \(\frac {1}{b}\)) + 9 + (c + \(\frac {1}{b}\) – 2a) (3a – \(\frac {1}{b}\) – 3)
Solution :

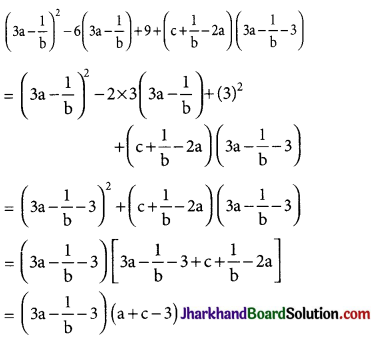
Question 17.
Factorise: 4(2a + 3b – 4c)² – (a – 4b + 5c)²
Solution :
4(2a + 3b – 4c)² – (a – 4b + 5c)²
= [2(2a + 3b – 4c)]² – (a – 4b + 5c)²
= (4a + 6b – 8c)² – (a – 4b + 5c)²
= [4a + 6b – 8c + a – 4b + 5c] [4a + 6b – 8c – a + 4b – 5c]
= (5a + 2b – 3c) (3a + 10b – 13c)

Question 18.
Factorise: 4x² + \(\frac{1}{4 x^2}\) + 2 – 9y²
Solution :

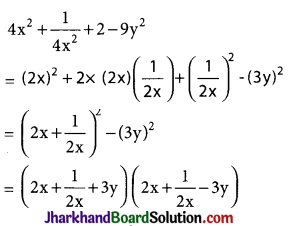
Question 19.
Factorise :
a⁴ + \(\frac{1}{a^4}\) – 3.
Solution :

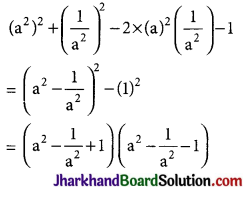
Question 20.
Factorise : x⁴ + x²y² + y⁴
Solution :
x⁴ + x²y² + y⁴ = (x²)² + 2.x².y² + (y²)² – x²y²
= (x² + y²)² – (xy)²
= (x² + y² + xy) (x² + y² – xy)

Question 21.
Factorise: 64a¹³b + 343ab¹³.
Solution :
64a¹³b + 343ab¹³ = ab[64a¹² + 343b¹²)
= ab[(4a⁴)³ + (7b⁴)³]
= ab[4a⁴ + 7b⁴) [(4a⁴)² – (4a⁴) (7b⁴) + (7b⁴)²]
= ab[4a⁴ + 7b⁴][16a⁸ – 28a⁴b⁴ + 49b⁸]

Question 22.
Factorise : p³q²x⁴ + 3p²qx³ + 3px² + \(\frac {x}{q}\) – q²r³x
Solution :
In above question, if we take common then it may become in the form of a³ + b³.
∴ p³q²x⁴ + 3p²qx³ + 3px² + \(\frac {x}{q}\) – q²r³x
= \(\frac {x}{q}\) [p³q³x³ + 3p²q²x² + 3pqx + 1 – q³r³]
= \(\frac {x}{q}\)(pqx)³ + 3(pqx)² × 1 + 3pqx × (1)² + (1)³ – q³r³]
Let pqx = A and 1 = B
= \(\frac {x}{q}\) [A³ + 3A²B + 3AB² + B³ – q³r³]
= \(\frac {x}{q}\) [(pqx + 1) – (qr)³]
= [pqx + 1 – qr] (pqx + 1)² + (pqx + 1)qr + (ar)]
= [pqx + 1 – qr] [p²q²x + 1 + 2pqx + pqxr + 4r + q²r²]

Question 23.
Factorise : x³ – 6x² + 32
Solution :
x³ + 32 – 6x² = x³ + 8 + 24 – 6x²
= [(x)³ + (2)³] + 6[4 – x²]
= (x + 2) [x² – 2x + 4] + 6[2 + x] [2 – x]
= (x + 2) [x² – 2x + 4 + 6(2 – x)]
= (x + 2) [x² – 2x + 4 + 12 – 6x]
= (x + 2) (x² – 8x + 16)
= (x + 2) (x – 4)²
= (x + 2) (x – 4) (x – 4)

Question 24.
Show that x = 2 is a zero of 2x³ + x² – 7x – 6.
Solution :
p(x) = 2x³ + x² – 7x – 6
p(2) = 2(2)³ + (2)² – 7(2) – 6
= 16 + 4 – 14 – 6 = 0
Hence x = 2 is a zero of p(x).

Question 25.
If x = \(\frac {4}{3}\) is a zero of the polynomial f(x) = 6x³ – 11x² + kx – 20 then find the value of k.
Solution :
f(x) = 6x³ – 11x + kx – 20
x = \(\frac {4}{3}\) is a zero of f(x)
⇒ f(\(\frac {4}{3}\)) = 0
⇒ 6(\(\frac {4}{3}\))³ – 11(\(\frac {4}{3}\))² + k(\(\frac {4}{3}\)) – 20 = 0
⇒ 6 × \(\frac{64}{9 \times 3}\) – 11 × \(\frac {16}{9}\) + \(\frac {4k}{3}\) – 20 = 0
⇒ 128 – 176 + 12k – 180 = 0
⇒ 12k + 128 – 356 = 0
⇒ 12k = 228
⇒ k = 19

Question 26.
If x = 2 and x = 0 are two zeroes of the polynomial f(x) = 2x³ – 5x² + ax + b, find the values of a and b.
Solution :
f(2) = 2(2)³ – 5(2)² + a(2) + b = 0
⇒ 16 – 20 + 2a + b = 0
⇒ 2a + b = 4 ………..(i)
⇒ f(0) = 2(0)³ – 5(0)² + a(0) + b = 0
⇒ b = 0
So, 2a = 4 ⇒ a = 2 [using (i)]
Hence, a = 2, b = 0

Question 27.
Find the remainder when f(x) = x³ – 6x² + 2x – 4 is divided by g(x) = 1 – 2x.
Solution :
1 – 2x = 0
2x = 1
x = \(\frac {1}{2}\)

Question 28.
The polynomials ax³ + 3x² – 13 and 2x³ – 5x + a are divided by x + 2 if the remainder in each case is the same, find the value of a.
Solution :
p(x) = ax³ + 3x² – 13 and q(x) = 2x³ – 5x + a
x + 2 = 0
⇒ x = – 2
p(-2) = q(-2)
⇒ a(-2)³ + 3(-2)² – 13 = 2(-2)³ – 5(-2) + a
⇒ – 8a + 12 – 13 = – 16 + 10 + a
⇒ – 9a = -5
⇒ a = \(\frac {5}{9}\)

Question 29.
Show that x + 1 and 2x – 3 are factors of 2x³ – 9x² + x + 12.
Solution :
To prove that (x + 1) and (2x – 3) are factors of p(x) = 2x³ – 9x² + x + 12, it is sufficient to show that p(-1) and P(\(\frac {3}{2}\)) both are equal to zero.
p(-1) = 2(-1)³ – 9(-1)² + (-1) + 12
= – 2 – 9 – 1 + 12 = – 12 + 12 = 0
p(\(\frac {3}{2}\)) = 2(\(\frac {3}{2}\))³ – 9(\(\frac {3}{2}\))² + \(\frac {3}{2}\) + 12
= \(\frac{27}{4}-\frac{81}{4}+\frac{3}{2}\) + 12
= \(\frac{27-81+6+48}{4}=\frac{81-81}{4}\) = 0
Hence, (x + 1) and (2x – 3) are the factors
2x³ – 9x² + x + 12.

Question 30.
Find α and β if x + 1 and x + 2 are factors of p(x) = x³ + 3x² – 2αx + β.
Solution :
When we put x + 1 = 0 or x = – 1 and x + 2 = 0 or x = – 2 in p(x)
Then, p(-1) = 0 and p(-2) = 0 as x + 1 and x + 2 are factors of p(x)
Therefore, p(-1) = (-1)³ + 3(-1)² – 2α(-1) + β = 0
⇒ – 1 + 3 + 2α + B = 0
⇒ β = – 2α – 2 ….(i)
And, p(-2) = (-2)³ + 3(-2)² – 2α(-2) + β = 0
⇒ – 8 + 12 + 4α + β = 0
⇒ β = – 4α – 4 ….(ii)
From equations (i) and (ii),
– 2α – 2 = – 4α – 4
⇒ 2α = -2
⇒ α = – 1
Put α = -1 in equation (i)
⇒ β = – 2(-1) – 2 = 2 – 2 =0.
Hence, α = – 1, β = 0.

Question 31.
Using factor theorem, factorize:
p(x) = 2x⁴ – 7x³ – 13x² + 63x – 45
Solution :
45 has ± 1, ± 3, ± 5, ± 9, ± 15, ± 45 as its factors
If we put x = 1 in p(x)
p(1) = 2(1)⁴ – 7(1)³ – 13(1)² + 63(1) – 45
= 2 – 7 – 13 + 63 – 45
= 65 – 65 = 0
∴ x – 1 is a factor of p(x) by factor theorem
Similarly, if we put x = 3 in p(x)
p(3) = 2(3)⁴ – 7(3)³ – 13(3)² + 63(3) – 45
= 162 – 189 – 117 + 189 – 45
= 162 – 162 = 0
Hence, x – 3 is the factor of p(x) by factor theorem.
p(x) = 2x⁴ – 7x³ – 13x² + 63x – 45
= 2x⁴ – 2x³ – 5x³ + 5x² – 18x² + 18x + 45x – 45
∴ p(x) = 2x³(x – 1) – 5x²(x – 1) – 18x(x – 1) + 45(x – 1)
⇒ p(x) = (x – 1)(2x³ – 5x² – 18x + 45)
⇒ p(x)= (x – 1)(2x³ – 6x² + x² – 3x – 15x + 45]
⇒ p(x) =(x – 1)[2x³(x – 3) + x(x – 3) – 15(x – 3)]
⇒ p(x) = (x – 1)(x – 3)(2x² + x – 15)
⇒ p(x) = (x – 1)(x – 3)(2x² + 6x – 5x – 15)
⇒ p(x) = (x – 1)(x – 3)[2x(x + 3) – 5(x + 3)]
⇒ p(x) = (x – 1)(x – 3)(x + 3)(2x – 5)

Question 32.
Factorise : x² – 31x + 220.
Solution :

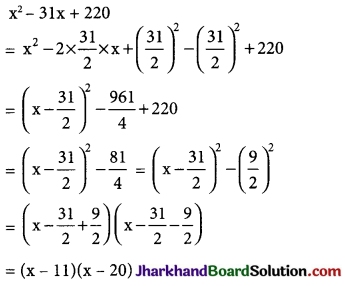
Question 33.
Factorise :
2x² + 12\(\sqrt{2}\)x + 35.
Solution :
2x² + 12\(\sqrt{2}\)x + 35
Product ac = 70 and b = 12\(\sqrt{2}\)
∴ Split the middle term as 7\(\sqrt{2}\) and 5\(\sqrt{2}\).
⇒ 2x² + 12\(\sqrt{2}\) x + 35
= 2x² + 7\(\sqrt{2}\)x + 5\(\sqrt{2}\)x + 35
= \(\sqrt{2}\)x[\(\sqrt{2}\)x + 7] + 5[\(\sqrt{2}\)x + 7]
= [\(\sqrt{2}\)x + 5]\(\sqrt{2}\)x + 7]

Question 34.
Factorise: x² – 14x + 24.
Solution :
Product ac = 24 and b = – 14
∴ Split the middle term as – 12 and – 2
⇒ x² – 14x + 24 = x² – 12x – 2x + 24
⇒ x(x – 12) – 2(x – 12) = (x – 12)(x – 2)

Question 35.
Factorise :
x² – \(\frac {13}{24}\)x – \(\frac {1}{12}\)
Solution :
x² – \(\frac {13}{24}\)x – \(\frac {1}{12}\) = \(\frac {1}{24}\) (24x² – 13x – 2)
ac = – 48 and b = – 13
∴ Wesplit the middle term as – 16x + 3x.
= \(\frac {1}{24}\)(24x² – 16x + 3x – 2)
= \(\frac {1}{24}\)[8x(3x – 2) + 1(3x – 2)]
= \(\frac {1}{24}\)(3x – 2)(8x + 1)

Question 36.
Factorise : \(\frac {3}{2}\)x² – 8x – \(\frac {35}{2}\)
Solution :
= \(\frac {1}{2}\)(3x² – 16x – 35)
= \(\frac {1}{2}\)(3x² – 21x + 5x – 35)
= \(\frac {1}{2}\)[3x(x – 7) + 5(x – 7)]
= \(\frac {1}{2}\)(x – 7)(3x + 5)

Question 37.
If f(x) = 2x³ – 13x² + 17x + 12 then find out the value of f(-2) and f(3).
Solution :
f(x) = 2x² – 13x² + 17x + 12
f(-2) = 2(-2)³ – 13(-2)² + 17 (-2) + 12
= – 16 – 52 – 34 + 12
= – 90
f(3) = 2(3)³ – 13(3)² + 17(3) + 12
= 54 – 117 + 51 + 12
= 0

Question 8.
Factorise: – 8 + 9(a – b)⁶ – (a – b)¹²
Solution :
– 8 + 9(a – b)⁶ – (a – b)¹²
Let (a – b)⁶ = x
Then – 8 + 9x – x² = – (x² – 9x + 8)
= – (x² – 8x – x + 8)
= – (x – 8)(x – 1)
= – [(a – b)⁶ – 8][(a – b)⁶ – 1]
= [1 – (a – b)⁶][(a – b)⁶ – 8]
= [(1)³ – {(a – b)²}³][{(a – b)²}³ – (2)³]
= [1 – (a – b)²][1 + (a – b)⁴ + (a – b)²][(a – b)² – 2][(a – b)⁴ + 4 + 2(a – b)²]

Multiple Choice Questions

Question 1.
The product of (x + a) (x + b) is:
(a) x² + (a + b) x + ab
(b) x² – (a – b) x + ab
(c) a² + (a – b)x + ab
(d) x² + (a – b)x – ab
Solution :
(a) x² + (a + b) x + ab

Question 2.
The value of 150 × 98 is :
(a) 10047
(b) 14800
(c) 14700
(d) 10470
Solution :
(c) 14700

Question 3.
The expansion of (x + y – z)² is :
(a) x² + y² + z² + 2xy + 2yz + 2zx
(b) x² + y² – z² – 2xy + yz + 2zx
(c) x² + y² + z² + 2xy – 2yz – 2zx
(d) x² + y² – z² + 2zy – 2yz – 2zx
Solution :
(c) x² + y² + z² + 2xy – 2yz – 2zx

Question 4.
The value of (x + 2y + 2z)² + (x – 2y – 2z)² is :
(a) 2x² + 8y² + 8z²
(b) 2x² + 8y² + 8z² + 8xyz
(c) 2x² + 8y² + 8z² – 8yz
(d) 2x² + 8y² + 8z² + 16yz
Solution :
(d) 2x² + 8y² + 8z² + 16yz

Question 5.
The value of 25x² + 16y² + 40xy at x = 1 and y = – 1 is :
(a) 81
(b) – 49
(c) 1
(d) None of these
Solution :
(c) 1

Question 6.
On simplifying (a + b)³ + (a – b)³ + 6a(a² – b²) we get:
(a) 8a²
(b) 8a²b
(c) 8a³b
(d) 8a³
Solution :
(d) 8a³

Question 7.
Find the value of \(\frac{a^3+b^3+c^3-3 a b c}{a b+b c+c a-a^2-b^2-c^2}\) when a = – 5, b = – 6, c = 10.
(a) 1
(b) -1
(c) 2
(d) -2
Solution :
(a) 1

Question 8.
In method of factorisation of an algebraic expression, which of the following statements is false?
(a) Taking out a common factor from two or more terms.
(b) Taking out a common factor from a group of terms.
(c) By using remainder theorem.
(d) By using standard identities.
Solution :
(c) By using remainder theorem.

Question 9.
Factors of (a + b)³ – (a – b)³ is:
(a) 2ab(3a² + b²)
(b) ab(3a² + b²)
(c) 2b(3a² + b²)
(d) 3a² + b²
Solution :
(c) 2b(3a² + b²)

Question 10.
Degree of zero polynomial is :
(a) 0
(b) 1
(c) Both 0 and 1
(d) Not defined
Solution :
(d) Not defined

Question 11.
Factors of (42 – x – x²) are:
(a) (x – 7)(x – 6)
(b) (x + 7)(x – 6)
(c) (x + 7)(6 – x)
(d) (x + 7) (x + 6)
Solution :
(c) (x + 7)(6 – x)

Question 12.
Factors of (x² + \(\frac{x}{6}-\frac{1}{6}\)) are :
(a) \(\frac {1}{6}\)(2x + 1)(3x + 1)
(b) \(\frac {1}{6}\)(2x + 1)(3x – 1)
(c) \(\frac {1}{6}\)(2x – 1) (3x – 1)
(d) \(\frac {1}{6}\)(2x – 1)(3x + 1)
Solution :
(d) \(\frac {1}{6}\)(2x – 1)(3x + 1)

Question 13.
Factors of polynomial x³ – 3x² – 10x + 24 are:
(a) (x – 2)(x + 3)(x – 4)
(b) (x + 2)(x + 3)(x + 4)
(c) (x + 2)(x – 3)(x – 4)
(d) (x – 2)(x – 3)(x – 4)
Solution :
(a) (x – 2)(x + 3)(x – 4)

Question 14.
If (x + a) is a factor of x² + px + q and x² + mx + n then the value of a is :
(a) \(\frac{m-p}{n-q}\)
(b) \(\frac{n-q}{m-p}\)
(c) \(\frac{n+q}{m+p}\)
(d) \(\frac{m+p}{n+q}\)
Solution :
(b) \(\frac{n-q}{m-p}\)