JAC Class 9 Maths Important Questions Chapter 2 बहुपद

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 2 बहुपद

प्रश्न 1.
बहुपद p(x) = 5x² – 3x +7 में x 1 रखने पर बहुपद का मान होगा :
(A) 9
(B) 11
(C) 12
(D) 3
हल :
p(x) = 5x² – 3x +7
x = 1 रखने पर,
P( 1 ) = 5 (1)² – 3 ( 1 ) + 7
= 5 – 3 + 7 = 9
अतः सही विकल्प ‘A’ है।

प्रश्न 2.
p(x) = 2x + 1 का एक शून्यक होगा :
(A) \(\frac {1}{2}\)
(B) 3
(C) –\(\frac {1}{2}\)
(D) 1
हल :
p(x) = 2x + 1
शून्यक होने के लिए p(x) = 0 होगा।
∴ 0 = 2x + 1 ⇒ x = – \(\frac {1}{2}\)
अतः सही विकल्प ‘C’ है।

प्रश्न 3.
x⁴ + x³ – 2x² + x + 1 को x – 1 से भाग देने पर प्राप्त शेषफल होगा :
(A) 0
(B) 2
(C) 1
(D) – 2
हल :
p(x) = x⁴ + x³ – 2x² + x + 1 को (x – 1) से शेषफल p (1) का मान (1) होता है।
∵ x – 1 = 0 ⇒ x = 1
p(1) = 1⁴ + 1³ – 2 (1)² + 1 + 1
= 1 + 1 – 2 + 1 +1 = 2
अतः सही विकल्प ‘B’ है।

प्रश्न 4.
व्यंजक (x – 3) बहुपद
p(x) = x³ + x² – 17x + 15
का गुणनखण्ड होगा, यदि :
(A) p(3) = 0
(B) p(-3) = 0
(C) P(-3) = 0
(D) p(-3) = – 3
हल :
p(x) = x³ + x² – 17x + 15
(x – 3), p(x) का एक गुणनखण्ड है, तो
x – 3 = 0, x = 3
अत: सही विकल्प ‘A’ है।

प्रश्न 5.
x³ – y³ का एक गुणनखण्ड है:
(A) x + y
(B) x² + y²
(C) x² – xy + y²
(D) x – y
हल :
x³ – y³ के गुणनखण्ड
= (x – y) (x² + xy + y²)
एक गुणनखण्ड (x – y) है। अतः सही विकल्प ‘D’ है।

प्रश्न 6.
x⁴ + 8x का एक गुणनखण्ड है:
(A) x + 2
(B) x – 2
(C) x + 8
(D) x² + 2x + 2
हल :
x⁴ + 8x = x(x³ + 8)
= x[(x)³ + (2)³]
= x(x + 2) (x² – 2x + 4)
एक गुणनखण्ड (x + 2) है अतः सही विकल्प ‘A’ है।

प्रश्न 7.
x³ – 8 का एक गुणनखण्ड है:
(A) x + 2
(B) x – 4
(C) x² + 2x + 4
(D) x² – 2x – 4
हल :
x³ – 8 = (x)³ – (2)³
= (x – 2) (x² + 2x + 4)
एक गुणनखण्ड (x² + 2x + 4 ) है अतः सही विकल्प ‘C’ है |

प्रश्न 8.
3y³ + 8y² – 1 का पूर्णांक शून्य है :
(A) 1
(B) – 1
(C) 0
(D) विद्यमान नहीं
हल :
3y³ + 8y² – 1 का पूर्णांक शून्य है।
y = 1 रखने पर, 3(1)³ + 8(1)² – 1
= 3 + 8 – 1 = 10 ≠ 0
y = – 1 रखने पर, 3(-1)³ + 8(-1)² – 1
= – 3 + 8 – 1 = 4 ≠ 0
y = 0 रखने पर, 3(0)³ + 8 × (0)² – 1
= – 1 ≠ 0
अतः व्यंजक में के स्थान पर 1, – 1 और 0 रखने पर शून्य नहीं आता है।
अतः सही विकल्प ‘D’ है।

प्रश्न 9.
सत्यापित कीजिए कि 2 और 0 बहुपद x² – 2x के शून्यक हैं।
हल:
p(x) = x² – 2x
p(2) = 2² – 2(2)
p(2) = 4 – 4 = 0
एवं p(0) = 0 – 0 = 0
अतः 2 और 0 दोनों ही बहुपद x² – 2x के शून्यक हैं। इति सिद्धम्

प्रश्न 10.
जाँच कीजिए कि बहुपद
q(t) = 4t³ + 4t² – t – 1, 2t + 1 का एक गुणज है।
हल :
बहुपद q(t), 2t + 1 का गुणज केवल तब होगा जब 2t + 1 से q(t) को भाग देने पर शेषफल शून्य आता हो ।
∴ 2t + 1 = 0
t = – \(\frac {1}{2}\)
\(q\left(-\frac{1}{2}\right)=4\left(-\frac{1}{2}\right)^3+4\left(-\frac{1}{2}\right)^2-\left(-\frac{1}{2}\right)\) – 1
= – 4 × \(\frac {1}{8}\) + 4 × \(\frac {1}{4}\) + \(\frac {1}{2}\) – 1
= – \(\frac {1}{2}\) + 1 + \(\frac {1}{2}\) – 1 = 0
अतः 2t + 1 दिए गये बहुपद q(t) का एक गुणज है।

प्रश्न 11.
सिद्ध कीजिए कि 5, बहुपद 2x³ – 7x² – 16x + 5 का शून्यक है।
हल :
5 बहुपद 2x³ – 7x² – 16x + 5 का शून्यांक है। बहुपद में x = 5 रखने पर,
2x³ – 7x² – 16x + 5 = 2(5)³ – 7(5)³ – 16(5) + 5
= 2 × 125 – 7(25) – 80 + 5
= 250 – 175 – 80 + 5
= 255 – 255 = 0
∵ x = 5 रखने पर बहुपद का मान शून्यक प्राप्त होता है।
अतः 5 बहुपद का पूर्णांक शून्यक होगा। इति सिद्धम्

प्रश्न 12.
a के किस मान के लिए बहुपद x³ + 2x² – 3ax – 8 में व्यंजक (x – 4) का पूरा-पूरा भाग जाता है?
हल :
बहुपद में x – 4 का भाग देने पर शेषफल f(4) प्राप्त होगा।
f(x) = x³ + 2x² – 3ax – 8 में x के स्थान पर 4 रखने पर
f(4) = (4)³ + 2(4)² – 3a(4) – 8 = 0
= 64 + 2 × 16 – 12a – 8 = 0
= 64 + 32 – 12a – 8 = 0
= 96 – 12a – 8 = 88 – 12a = 0
⇒ 12a = 88
∴ a = \(\frac {88}{12}\) = \(\frac {22}{3}\)
अतः a = \(\frac {22}{3}\)

प्रश्न 13.
यदि x² + \(\frac{1}{x^2}\) = 48 हो तब (x + \(\frac {1}{x}\)) का मान ज्ञात करो ।
हल :
सूत्र से,

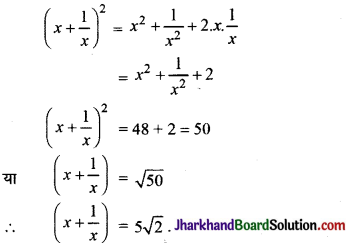
प्रश्न 14.
यदि x³ + a³ में x + a का भाग दिया जाए, तो शेषफल ज्ञात कीजिए ।
हल:

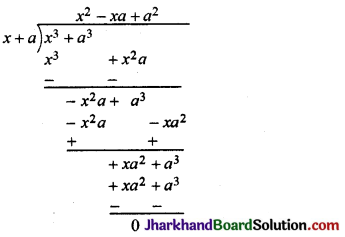
∴ शेषफल = 0

प्रश्न 15.
(2x + 3)³ + (3x – 2)³ – (5x + 1)³ क गुणनखण्ड कीजिए।
हल :
माना
2x + 3 = a
3x – 2 = b
– (5x + 1) = c
अब a + b + c = (2x + 3) + (3x – 2 ) – (5x + 1)
= 2x + 3 + 3x – 2 – 5x – 1
= 5x – 5x + 3 – 3 = 0
सर्वसमिका a³ + b³ + c³ = 3abc
a, b तथा c के मान रखने पर
(2x + 3 )³ + (3x – 2)³ – (5x + 1 )³
= 3 × (2x + 3) × (3x – 2) × [- (5x + 1) ]
= – 3 (2x + 3) (3x – 2) (5x + 1).

प्रश्न 16.
सिद्ध कीजिए कि x² + 6x + 15 का कोई शून्य नहीं होता।
हल :
माना कि f(x) = x² + 6x + 15
∴ f(x) = {x2 + 2 (3)x + 9} + 6
= (x + 3)² + 6
यहाँ x के प्रत्येक वास्तविक मान के लिए (x + 3)² का मान कभी भी ऋणात्मक नहीं हो सकता। अतः (x + 3)² का मान सदैव शून्य से बड़ा ही रहेगा। परिणामस्वरूप f(x) का मान भी 6 या उससे अधिक होगा।
इसलिए (x) का कोई शून्य विद्यमान नहीं है।

प्रश्न 17.
गुणनखण्ड कीजिए:
(i) x³ – 64
(ii) (2x – 1)³ – (x – 1)³
हल :
(i) x³ – 64 = (x)³ – (4)³
∵ a³ – b³ = (a – b) (a² + ab + b²)
∴ (x – 4) [(x)² + (x)(4) + (4)²]
= (x – 4) (x² + 4x + 16)

(ii) (2x – 1)³ – (x – 1)³
= [(2x – 1) – (x – 1)] [(2x – 1)² + (2x – 1) (x – 1) + (x – 1)³]
= x[4x² – 4x + 1 + 2x² – 3x + 1 + x² – 2x + 1]
= x(7x² – 9x+3).

प्रश्न 18.
(3a + 4b + 5c)² को प्रसारित रूप में लिखिए।
हल :
सर्वसमिका (x + y + z)² = x² + y² + z² + 2xy + 2yz +2zx
(3a + 4b + 5c)² = (3a)² + (4b)² + (5c)² + 2(3a)(4b) + 2 (4b) (5c) + 2 (5c) (3a)
= 9a² + 16b² + 25c² + 24ab + 40bc + 30ac.

प्रश्न 19.
4x² + y² + z² – 4xy – 2yz + 4xz को गुणनखण्ड कीजिए।
हल :
(2x)² + (y)² + (z)² + 2(2x)(-y) + 2(- y)(z) + 2(2x)(z)
सर्वसमिका (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
= [2x + (-y) + z]²
= (2x – y + z)²
= (2x – y + z) (2x – y + z).

प्रश्न 20.
उपयुक्त सर्वसमिकाएँ प्रयोग करके, निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए :
(i) (104)³
(ii) (999)³
हल :
(i) यहाँ (104)³ = ( 100 + 4)³
=(100)³ + (4)³ + 3(100)(4)(100 + 4)
[सर्वसमिका (a + b)³ = a³ + b³ + 3ab (a + b)]
= 1000000 + 64 + 124800 = 1124864.

(ii) यहाँ (999)³ = ( 1000 – 1)³
= (1000)³ – (1)³ – 3(1000)(1)(1000 – 1)
[सर्वसमिका a³ – b³ = a³ – b³ – 3ab (a + b)]
= 1000000000 – 1 – 2997000
= 997002999.

प्रश्न 21.
8x³ + 27y³ + 36x²y + 54xy – 2 के गुणनखण्डन कीजिए।
हल :
दिए हुए व्यंजक को इस प्रकार लिखा जा सकता है:
(2x)³ + (3y)³ + 3(4x²)(3y) + 3(2x)(9y²)
[सर्वसमिका (a + b)³ = a³ + b³ + 3a²b + 3ab²)
= (2x)³ + (3y)³ + 3(2x)²(3y) + 3(2x)(3y)²
= (2x + 3y)³
= (2x + 3y) (2x + 3y) (2x + 3y).

प्रश्न 22.
(4a – 2b – 3c)² का प्रसार कीजिए।
हल :
सर्वसमिका
(x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
∴ (4a – 2b – 3c)² = [4a + (-2b) + (- 3c)]²
= (4a)² + (-2b)² + (- 3c)² + 2(4a)(-2b) + 2(-2b) (- 3c) + 2 (-3c) (4a)
= 16a² + 4b² + 9c² – 16ab + 12bc – 24ac.

प्रश्न 23.
यदि (x – \(\frac {1}{x}\))² = 5 तो(x² – \(\frac{1}{x^2}\)) का मान ज्ञात करो ।
हल :
सूत्र,
(a – b)² = a² + 2ab – b²
(x – \(\frac {1}{x}\))² = x² + \(\frac{1}{x^2}\) – 2.x.\(\frac {1}{x}\)
5 = (x² + \(\frac{1}{x^2}\)) – 2
∴ x² + \(\frac{1}{x^2}\) = 7

प्रश्न 24.
प्रदर्शित कीजिए कि बहुपद x¹⁰ – 1 और x¹¹ – 1 का एक गुणनखण्ड (x – 1) है ।
हल :
माना
p(x) = x¹⁰ – 1
तथा
q(x) = x¹¹ – 1
(x – 1) गुणनखण्ड प्रदर्शित करने के लिए p(x) = 0, q(x) = 0 दिखाना पड़ेगा।
∴ p(x) = x¹⁰ – 1
p(1) = (1)¹⁰ – 1
P(1) = 1 – 1
P(1) = 0

तथा q(x) = x¹¹ – 1
q (1) = (1)¹¹ – 1
q (1) = 1 – 1
q(1) = 0
अत: (x – 1), बहुपद (x¹⁰ – 1) तथा (x¹¹ – 1) का एक गुणनखण्ड है।

प्रश्न 25.
व्यंजक x⁸ – y⁸ के गुणनखण्ड कीजिए।
हल :
सर्वसमिका a² + b² = (a + b) (a – b) से, (x⁴)² – (y⁴)²
= (x⁴ – y⁴) (x⁴ + y⁴)
= [(x²)² – (y²)²] [x⁴ + y⁴]
(x² – y²) (x² + y²) (x⁴ + y⁴)
पुनः (x – y) (x + y) (x² + y²) (x⁴ + y⁴)

प्रश्न 26.
यदि (x² + \(\frac{1}{x^2}\)) = 83 तो (x³ – \(\frac{1}{x^3}\)) का मान ज्ञात करो ।
हल :

प्रश्न 27.
व्यंजक (x¹² – y¹²) के गुणनखण्ड कीजिए।
हल :
x¹² – y¹² = (x⁶)² – (y⁶)²,
सर्वसमिका a² – b² = (a – b)(a + b)
= (x⁶ + y⁶)(x⁶ – y⁶)
= (x⁶ + y⁶) [(x³)² – (y³)²]
= (x⁶ + y⁶) [x³ + y³] [x³ – y³]
सर्वसमिका a³ + b³ = (a + b) (a² – ab + b²)
तथा a³ – b³ = (a – b) (a² + ab + b²)
= (x⁶ + y⁶) [(x + y) (x² – xy + y²) (x – y) (x² + xy + y²)]
= [(x²)³ + (y²)³] [(x + y) (x – y) (x² – xy + y²) (x² + xy + y²)]
= (x² + y²) (x⁴ – x²y² + y⁴) (x + y) (x – y)(x² – xy + y²)(x² + xy + y²)
अतः x¹² – y¹² = (x + y) (x – y)(x² + y²) (x⁴ – x²y² + y⁴)(x² – xy + y²)(x² + xy + y²)