Students should go through these JAC Class 9 Maths Notes Chapter 6 रेखाएँ और कोण will seemingly help to get a clear insight into all the important concepts.
JAC Board Class 9 Maths Notes Chapter 6 रेखाएँ और कोण
(1) रेखा : (i) रेखा अनन्त बिन्दुओं का वह समूह है जिसका कोई अन्त बिन्दु नहीं होता।

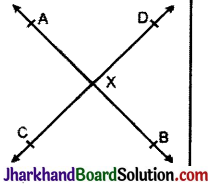
(2) प्रतिच्छेदी रेखाएँ: जब दो रेखाएँ आपस में एक-दूसरे को काटती हैं, प्रतिच्छेदी रेखाएँ कहलाती हैं। जिस बिन्दु पर वे एक-दूसरे को प्रतिच्छेद करती हैं, वह बिन्दु प्रतिच्छेदन बिन्दु कहलाता हैं।
AB व CD प्रतिच्छेदी रेखाएँ हैं तथा X प्रतिच्छेदन बिन्दु है।
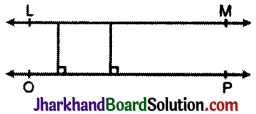
(3) समान्तर रेखाएँ : वे रेखाऐं जो एक ही समतल में होते हुए भी कभी प्रतिच्छेद नहीं करती हैं तथा जिनके मध्य की दूरी अनन्त तक अचर रहती है। समान्तर रेखाऐं कहलाती हैं।
LM व OP समान्तर रेखाएँ हैं।
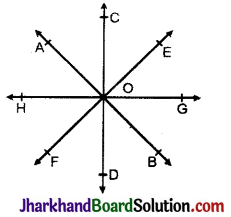
(4) संगामी रेखाएँ : तीन या तीन से अधिक ऐसी रेखाएँ जो एक ही बिन्दु से होकर गुजरें या उनका एक उभयनिष्ठ बिन्दु हो, संगामी रेखाएँ कहलाती हैं। AB, CD, EF, GH चार संगामी रेखाएँ हैं तथा उभयनिष्ठ बिन्दु O है।
![]()
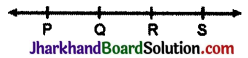
(5) सरेख बिन्दु किसी सरल रेखा पर स्थित समस्त बिन्दु सरेख बिन्दु कहलाते हैं।
P Q R S सरेख बिन्दु हैं।
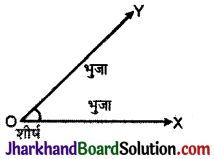
(6) कोण : कोण वह आकृति है जो उभयनिष्ठ प्रारम्भ वाली दो किरणों से बनती है।
दो कोण आसन्न कोण कहलाते हैं, यदि
(i) उनका एक ही शीर्ष बिन्दु हो, तथा
(ii) एक कोण की दूसरी भुजा उभयनिष्ठ भुजा के एक ओर हो और दूसरे कोण की दूसरी भुजा उभयनिष्ठ भुजा के दूसरी ओर हो।
दो आसन्न कोणों को कोणों का रैखिक युग्म (A linear pair of angles) कहते हैं, यदि उभयनिष्ठ भुजा के अतिरिक्त भुजाएँ दो विपरीत किरणें हों।
यदि किसी किरण का मूल बिन्दु एक रेखा पर स्थित हो, तो इस प्रकार बने दो आसन्न कोणों का योग दो समकोण अथवा 180° होता है।
किरणें \(\overrightarrow{O X}\) तथा \(\overrightarrow{O Y}\), ∠XOY या ∠YOX की भुजाएँ कहलाती हैं। उभयनिष्ठ बिन्दु ‘O’ को कोण का शीर्ष कहते हैं।
(7) कोणो का वर्गीकरण :
(a) सम्पूरक कोण ऐसे दो कोण जिनकी माप का योगफल 180° के बराबर हो, एक-दूसरे के सम्पूरक कोण कहलाते हैं।
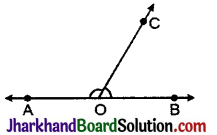
चित्र में ∠AOC और ∠BOC एक-दूसरे के सम्पूरक कोण हैं।
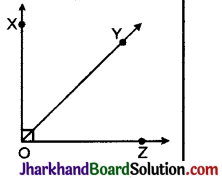
(b) पूरक कोण ऐसे कोण युग्म जिनका योग 90° होता है परस्पर पूरक कोण कहलाते हैं।
चित्र में ∠XOY और ∠YOZ एक-दूसरे के पूरक कोण हैं।
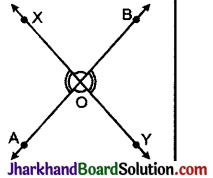
(8) शीर्षाभिमुख कोण यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करें, तो प्रतिच्छेद बिन्दु पर एक-दूसरे के विपरीत बने कोण, शीर्षाभिमुख कोण कहलाते हैं। शीर्षाभिमुख कोण आपस में बराबर होते हैं।
चित्र में रेखाएँ AB तथा XY एक-दूसरे को O बिन्दु पर प्रतिच्छेद करती हैं और इस प्रकार बिन्दु ‘O’ पर बने शीर्षाभिमुख ∠XOB = ∠AOY तथा ∠XOA = ∠BOY.
![]()
(9) समान्तर रेखाएँ और तिर्यक रेखा एक सरल रेखा जो दो या दो से अधिक रेखाओं को भिन्न बिन्दुओं पर प्रतिच्छेद करती है, तिर्यक रेखा कहलाती है। चित्र में रेखा l समान्तर रेखाओं m और n को क्रमश: P और Q बिन्दु पर काटती है। रेखा l, रेखाओं m और n के लिए तिर्यक रेखा है। प्रत्येक बिन्दु P और Q पर चार-चार कोण क्रमश: ∠1, ∠2, ∠3, ∠4 तथा ∠5, ∠6, ∠7, ∠8 बन रहे हैं।
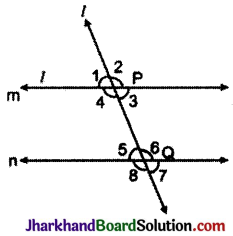
अन्त: कोण : ∠3, ∠4, ∠5 तथा ∠6 अन्तः कोण कहलाते हैं।
बाह्य कोण ∠1, ∠2, ∠7 तथा ∠8 बाह्य कोण कहलाते हैं। कोणों के युग्मों की स्थिति निम्न प्रकार होती है।
(a) संगत कोण (Corresponding angles) :
(i) ∠1 और ∠5
(ii) ∠2 और ∠6
(iii) ∠4 और ∠8
(iv) ∠3 और ∠7
(b) एकान्तर अन्तः कोण (Alternate interior angles) :
(i) ∠4 और ∠6
(ii) ∠3 और ∠5
(c) एकान्तर बाह्य कोण (Alternate exterior angles) :
(i) ∠1 और ∠7
(ii) ∠2 और ∠8
(d) तिर्यक रेखा के एक ही और के अन्तः कोण :
(i) ∠4 और ∠5
(ii) ∠3 और ∠6
(e) शीर्षाभिमुख कोण (Vertically opposite angles) :
(∠1, ∠3), (∠2, ∠4), (∠5, ∠7), (∠6, ∠8)
सामान्यतः ऊपर दिए गए कोण युग्मों के मध्य कोई सम्बन्ध नहीं होता है, लेकिन यदि दो या दो से अधिक समान्तर रेखाओं को एक तिर्यक रेखा काटे, तो
- संगत कोण समान होते हैं।
- एकान्तर कोण समान होते हैं।
- अन्तःकोण सम्पूरक होते हैं।
- एकान्तर बाह्य कोण समान होते हैं।