Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.3 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 10 वृत्त Exercise 10.3
प्रश्न 1.
वृत्तों के कई युग्म (जोड़े) खींचिए। प्रत्येक युग्म में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है ?
हल:
प्रश्न के निर्देश के अनुसार नीचे विभिन्न वृत्तों के युग्म खींचे जा सकते हैं :
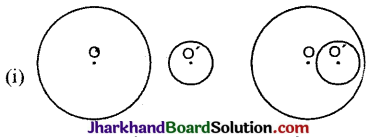
दोनों युग्मों में कोई बिन्दु उभयनिष्ठ नहीं है।
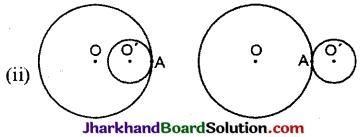
दोनों युग्मों में केवल एक बिन्दु उभयनिष्ठ है।
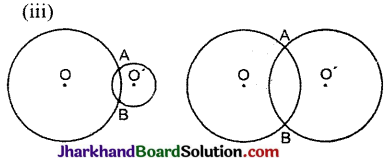
प्रत्येक युग्म में दो बिन्दु उभयनिष्ठ हैं।
अतः दो वृत्तों के उभयनिष्ठ विन्दुओं की अधिकतम संख्या = 2.
प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया गया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
हल:
दिया है: अज्ञात केन्द्र वाला एक वृत्त।
ज्ञात करना है: वृत्त का केन्द्र।
रचना: (1) वृत्त की जीवाएँ AB व BC खींची।
(2) जीवा AB व जीवा BC के लम्ब समद्विभाजक खींचे जो परस्पर बिंदु O पर काटते हैं।
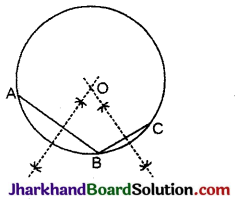
बिन्दु O वृत्त का अभीष्ट केन्द्र है।
![]()
प्रश्न 3.
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समृद्विभाजक पर स्थित हैं।
हल:
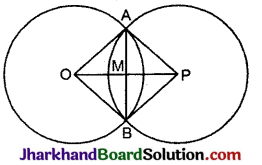
दिया है: वृत्त C (O, r) तथा C’ (P, r’) परस्पर A, B पर प्रतिच्छेदित करते हैं।
सिद्ध करना है: OP, जीवा AB का लम्ब समद्विभाजक है।
रचना: OA, OB, PA और PB को मिलाया।
उपपत्ति: ΔOAP और ΔOBP में,
AO = OB (एक ही वृत्त की त्रिज्याएँ)
PA = PB (एक ही वृत्त की त्रिज्याएँ)
OP = OP (उभयनिष्ठ)
∴ ΔOAP ≅ ΔOBP (SSS नियम से)
∠AOP = ∠BOP
⇒ ∠AOM = ∠BOM ……..(1)
अब ΔAOM और ΔBOM में,
OA = OB (एक ही वृत्त की त्रिज्याएँ)
∠AOM = ∠BOM [समी. (1) से]
OM = OM (उभयनिष्ठ)
ΔAOM ≅ ΔBOM (SAS नियम से)
AM = BM ……(2)
और ∠AMO = ∠BMO ……(3)
परन्तु ∠AMO + ∠BMO = 180°
⇒ ∠AMO + ∠AMO = 180° [समी. (3) से]
2∠AMO = 180°
∠AMO = 90°∠BMO …… (4)
समीकरण (2) और (4) से, OP जीवा AB का लम्ब समद्विभाजक है। इति सिद्धम्।