JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.7

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

प्रश्न 1.
उस लम्बवृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी :
(i) त्रिज्या 6 सेमी और ऊँचाई 7 सेमी है।
(ii) त्रिज्या 3.5 सेमी और ऊँचाई 12 सेमी है।
हल:
(i) लंम्बवृत्तीय शंकु की त्रिज्या (r) = 6 सेमी तथा ऊँचाई (h) = 7 सेमी।
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times(6)^2 \times 7\) घन सेमी
= 264 घन सेमी।
अतः लम्बवृत्तीय शंकु का आयतन 264 घन सेमी।

(ii) लम्बवृत्तीय शंकु की त्रिज्या (r) = 3.5 सेमी
= \(\frac{7}{2}\) सेमी
शंकु की ऊँचाई (h) = 12 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) × πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 12\) घन सेमी
= 154 घन सेमी
अतः लम्बवृत्तीय शंकु का आयतन = 154 घन सेमी।

प्रश्न 2.
शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए, जिसकी:
(i) त्रिज्या 7 सेमी और तिर्यक ऊंचाई 25 सेमी है।
(ii) ऊंचाई 12 सेमी और तिर्यक ऊंचाई 13 सेमी है।
हल:
(i) यहाँ, r = 7 सेमी और l = 25 सेमी
माना शंकु की ऊँचाई h सेमी है, तब
∴ l² = h² + r²
h² = l² – r² = 25² – 7²
= 625 – 49
= 576
∴ h = \(\sqrt{576}\) = 24 सेमी
शंक्वाकार बर्तन का आयतन = \(\frac{1}{3}\) πr²h
= \(\left(\frac{1}{3} \times \frac{22}{7} \times 7 \times 7 \times 24\right)\) सेमी³
= 1232 सेमी³
∴ बर्तन की धारिता (लीटर में)
= \(\left(\frac{1232}{1000}\right)\) लीटर = 1.232 लीटर।

(ii) यहाँ h= 12 सेमी और l = 13 सेमी
माना शंकु के आधार की त्रिज्या सेमी है।
तब, r² = l² – h² = 13² – 12²
= 169 – 144 = 25
⇒ r = \(\sqrt{25}\) = 5 सेमी
शंक्वाकार बर्तन का आयतन = \(\frac{1}{3}\) πr²h
= \(\left(\frac{1}{3} \times \frac{22}{7} \times 5 \times 5 \times 12\right)\) सेमी³
= \(\frac{2200}{7}\) सेमी³
∴ लीटर में बर्तन की धारिता (आयतन) = \(\left(\frac{2200}{7} \times \frac{1}{1000}\right)\) लीटर
(∵ 1000 घन सेमी = 1 लीटर)
= \(\frac{11}{35}\) लीटर।

प्रश्न 3.
एक शंकु की ऊंचाई 15 सेमी है। यदि इसका आयतन 1570 सेमी³ है, तो इसके आधार की त्रिज्या ज्ञात कीजिए।
(π = 3.14 प्रयोग कीजिए।)
हल:
यहाँ, h = 15 सेमी और आयतन = 1570 सेमी³
माना शंकु के आधार की त्रिज्या सेमी है।
आयतन = 1570 सेमी³
\(\frac{1}{3}\) πr²h = 1570
\(\frac{1}{3}\) × 3.14 × r² × 15 = 1570
r² = \(\frac{1570}{3.14 \times 5}\) = 100
∴ r = \(\sqrt{100}\) = 10
अतः शंकु के आधार की त्रिज्या 10 सेमी है।

प्रश्न 4.
यदि 9 सेमी ऊँचाई वाले एक लम्बवृत्तीय शंकु का आयतन 48π सेमी है। इसके आधार का व्यास ज्ञात कीजिए।
हल:
शंकु की ऊँचाई (h) = 9 सेमी
शंकु का आयतन = 48π सेमी³
\(\left(\frac{1}{3} \pi r^2 h\right)\) = 48π सेमी³
\(\frac{1}{3}\) × πr² × 9 = 48π
r² = \(\frac{48 \pi \times 3}{\pi \times 9}\) सेमी²
= 16 सेमी²
∴ r = \(\sqrt{16}\) सेमी = 4 सेमी
⇒ 2r = 2 × 4 सेमी = 8 सेमी
अंतः शंकु के आधार का व्यास 8 सेमी।

प्रश्न 5.
ऊपरी व्यास 3.5 मीटर वाले शंकु के आकार का एक गड्डा 12 मीटर गहरा है। इसकी धारिता किलोलीटर में कितनी है ?
हल:
गड्ढे का ऊपरी व्यास = 3.5 मीटर
∴ गड्ढे की त्रिज्या (r) = \(\frac{3.5}{2}\) मीटर
= \(\frac{35}{2 \times 10}\) मीटर = \(\frac{7}{4}\) मीटर
गड्ढे की ऊँचाई (h) = 12 मीटर
∴ गड्ढे का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times 12\) मीटर³ = \(\frac{154}{4}\) मीटर³
∵ 1 मी = 1000 लीटर = 1 किलो लीटर
∴ 38.5 मी³ = 38.5 किलो लीटर
अतः गढ्ढे की धारिता = 38.5 किलो लीटर

प्रश्न 6.
एक लम्बवृत्तीय शंकु का आयतन 9856 सेमी³ है। यदि इसके आधार का व्यास 28 सेमी है, तो ज्ञात कीजिए:
(i) शंकु की ऊंचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल।
हल:
(i) शंकु के आधार का व्यास 28 सेमी
∴ त्रिज्या = r = \(\frac{28}{2}\) सेमी
= 14 सेमी
शंकु का आयतन = 9856 सेमी³
⇒ \(\frac{1}{3}\) πr²h = 9856 सेमी³
⇒ \(\frac{1}{3} \times \frac{22}{7}\) × 14 × 14 × h = 9856
⇒ h = \(\frac{9856 \times 3 \times 7}{22 \times 14 \times 14}\)
= 48 सेमी
अतः शंकु की ऊँचाई = 48 सेमी।

(ii) माना शंकु की तिर्यक ऊँचाई l है, तब
l² = h² + r²
= 48² + 14²
= 2304 + 196 = 2500
∴ l = \(\sqrt{2500}\) = 50 सेमी
अतः शंकु की तिर्यक् ऊँचाई = 50 सेमी

(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 14 × 50
= 2,200 सेमी²।

प्रश्न 7.
भुजाओं 5 सेमी, 12 सेमी और 13 सेमी वाले एक समकोण त्रिभुज ABC को भुजा 12 सेमी के परितः घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
हल:
∵ ΔABC को 12 सेमी वाली भुजा AB के परित: घुमाए जाने पर प्राप्त निम्नलिखित शंक्वाकार ठोस आकृति प्राप्त होती हैं जिसमें

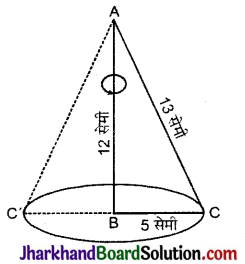
∴ शंकु की ऊँचाई AB = 12 सेमी
और शंकु की त्रिज्या CB = शंकु की दूसरी भुजा
= 5 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × π × (5)² × 12
= 100π घन सेमी।
अतः प्राप्त शंकु का आयतन = 100π घन सेमी।

प्रश्न 8.
यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 सेमी के परितः घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्न 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
हल:
…. ΔABC को 5 सेमी वाले भुजा के परितः घुमाए जाने पर निम्नांकित शंक्वाकार आकृति प्राप्त होती है जिसमें

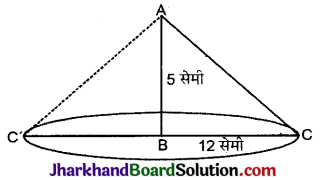
∴ शंकु की ऊँचाई (h) = 5 सेमी
और आधार की त्रिज्या (r) = दूसरी भुजा
= 12 सेमी
∴ शंकु का आयतन = \(\frac{1}{3}\) πr²h
\(\frac{1}{3}\) × π × (12)² × 5 घन सेमी
= 240π घन सेमी
अतः प्राप्त शंकु का आयतन = 240π घन सेमी।
तब प्रश्न 7 व प्रश्न 8 से प्राप्त ठोसों के आयतनों का अनुपात
= 100π : 240π
= 5 : 12.

प्रश्न 9.
गेहूँ की एक ढेरी 10.5 मीटर व्यास और 3 मीटर ऊँचाई वाले एक शंकु के आकार की है इसका ‘आयतन ज्ञात कीजिए। इस बेरी को वर्षा से बचाने के लिए केनवास से ढका जाता है। वांछित केनवास का क्षेत्रफल ज्ञात कीजिए।
हल:
गेहूँ की ढेरी से बने शंकु की ऊँचाई (h) = = 3 मीटर
तथा आधार का व्यास = 10.5 मीटर = \(\frac{21}{2}\) मीटर
∴ आधार की त्रिज्या (r) = \(\frac{21}{2 \times 2}=\frac{21}{4}\) मीटर
∴ गेहूँ की ढेरी (शंकु) का आयतन = \(\frac{1}{3}\) πr2h
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{21}{4} \times \frac{21}{4} \times 3\) घन मीटर
= \(\frac{693}{8}\) घन मीटर
= 86.625 घन मीटर।

∴ ढेरी को ढकने के लिए आवश्यक केनवास = गेहूँ की ढेरी का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7} \times \frac{21}{4} \times 6.05\)
= 99.825 वर्ग मीटर
अत: गेहूँ की ढेरी (शंकु) को ढकने के लिए आवश्यक केनवास का क्षेत्रफल
= 99.825 वर्ग मीटर।