Jharkhand Board JAC Class 9 Maths Solutions Chapter 14 सांख्यिकी Ex 14.4 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 14 सांख्यिकी Exercise 14.4
प्रश्न 1.
एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए 2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल:

पुनः 3 का आँकड़ा सबसे अधिक अर्थात् 4 बार आया है। अतः बहुलक = 3.
![]()
प्रश्न 2.
गणित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए:
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
इन आँकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल:

दिये गए आँकड़ों को आरोही क्रम में लिखने पर
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98.
यहाँ N = 15 पद है, जो कि विषम है।
∴ माध्यिका = \(\frac{N+1}{2}\) वाँ पद = \(\frac{15+1}{2}\) वाँ पद = 8वाँ पद
अतः प्राप्तांकों का माध्यक = 8वें पद का मान = 52
प्राप्त आँकड़ों से स्पष्ट है कि सबसे प्राप्तांक 52, 3 छात्रों के हैं जो सर्वाधिक हैं।
∴ दिये गये आँकड़ों का बहुलक = 52.
प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों का माध्यक 63 हो, तो x का मान ज्ञात कीजिए:
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
हल:
पदों की संख्या (N) = 10, सम संख्या हैं।
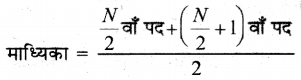

अत: x का मान 62 है।
![]()
प्रश्न 4.
आँकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए।
हल:
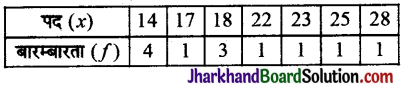
सबसे अधिक बारम्बारता 4 है। इसके संगत चर का मान 14 है।
अत: बहुलक = 14.
प्रश्न 5.
निम्नलिखित सारणी से एक फैक्ट्री में काम कर रहे 60 कर्मचारियों का माध्य वेतन ज्ञात कीजिए :
| वेतन (रुपयों मे) | कर्मचारियों की संख्या |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| कुल योग | 60 |
हल:
माध्य वेतन की आगणन तालिका
| वेतन रुपये में (x) | कर्मचारियों की संख्य (f) | (f × x) |
| 3000 | 16 | 48000 |
| 4000 | 12 | 48000 |
| 5000 | 10 | 50000 |
| 6000 | 8 | 48000 |
| 7000 | 6 | 42000 |
| 8000 | 4 | 32000 |
| 9000 | 3 | 27000 |
| 10000 | 1 | 10000 |
| येग | Σ f = 60 | Σ fx = 305000 |
माध्य = \(\frac{\sum f x}{\sum f}\) = \(\frac{305000}{60}=\frac{15250}{3}\) = 5083.33
अतः फैक्ट्री के 60 कर्मचारियों का माध्य वेतन = ₹ 5083.33 रु.।
![]()
प्रश्न 6.
निम्न स्थिति पर आधारित एक उदाहरण दीजिए:
(i) माध्य ही केन्द्रीय प्रवृत्ति की उपयुक्त माप है।
(ii) माध्य केन्द्रीय प्रवृत्ति की उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
हल:
(i) माध्य सम्बन्धित आँकड़ों का औसत (Average) होता है। अतः यह केन्द्रीय प्रवृत्ति की उपयुक्त माप है;
जैसे : चार विद्यार्थियों के अंग्रेजी के टेस्ट में प्राप्तांक क्रमश: 6, 5, 4 और 9 है इनका माध्य = \(\frac{6+4+5+9}{4}=\frac{24}{4}\) = 6
जो कि यह प्रमाणित करता है कि यह सभी प्राप्तांकों के निकट है और उनका प्रतिनिधित्व करने में सक्षम है।
(ii) मान लिया किसी मिनी बस में किन्हीं 5 दिनों में क्रमश: 10, 16, 24, 20 और 13 यात्री यात्रा करते हैं, तब इसमें प्रतिदिन यात्रा करने वाले यात्रियों का माध्य = \(\frac{10+16+24+20+13}{5}=\frac{83}{5}\) = 16.6.
परन्तु 16.6 वास्तविक यात्रियों के किसी भी प्रेक्षण का प्रतिनिधित्व नहीं करता क्योंकि अपूर्ण यात्रियों की सम्भाव्यता ही परिकल्पना से परे है। इस प्रकार माध्य केन्द्रीय प्रवृत्ति की वास्तविक एवं उपयुक्त माप नहीं है।
अब यदि हम इनके माध्यक पर विचार करें, तो
आरोही क्रम में आँकड़ों को व्यवस्थित करने पर 10, 13, 16, 20, 24
n = 5, माध्यक पद = \(\frac{N+1}{2}=\frac{5+1}{2}\) = 3वाँ पद पद
∴ माध्यक = 3वें पद का मान = 16 यात्री
अतः माध्यक केन्द्रीय प्रवृत्ति की उपयुक्त माप है।