JAC Class 9 Maths Solutions Chapter 2 बहुपद Ex 2.4

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 बहुपद Ex 2.4 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 2 बहुपद Exercise 2.4

प्रश्न 1.
बताइए कि निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखण्ड x + 1 है:
(i) x + x² + x + 1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 + \(\sqrt{2}\)) x + \(\sqrt{2}\)
हल:
(i) माना p(x) = x³ + x² + x + 1
(x + 1), p(x) का गुणनखण्ड होगा यदि p(-1) = 0.
∴ p(-1) = (-1)³ + (-1)² + (-1) + 1
= -1 + 1 – 1 + 1
P(1) = 0
अत: (x + 1), x³ + x² + x + 1 का गुणनखण्ड है।

(ii) माना p(x) = x⁴ + x³ + x² + x + 1
(x + 1), p(x) का गुणनखण्ड होगा यदि p(-1) = 0.
∴ p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
= 1 – 1 + 1 – 1 + 1 ≠ 0
अत: (x + 1), बहुपद p(x) का गुणनखण्ड नहीं है।

(iii) p(x) = x⁴ + 3x³ + 3x² + x + 1
(x + 1), p(x) का गुणनखण्ड होगा यदि p(-1) = 0.
∴ p (-1) = (-1)⁴ + 3(-1)³ + 3(-1)² + (-1) + 1
= 1 – 3 + 3 – 1 + 1 = 1
⇒ 1 ≠ 0
अत: (x + 1), बहुपद p(x) का गुणनखण्ड नहीं है।

(iv) माना p(x) = x³ – x² – (2 + \(\sqrt{2}\)) x + \(\sqrt{2}\)
(x + 1), p(x) का गुणनखण्ड होगा यदि p(-1) = 0
p(-1) = (-1)³ – (-1)² – (2 + \(\sqrt{2}\)) (-1) + \(\sqrt{2}\)
= – 1 – 1 + 2 + \(\sqrt{2}\) + \(\sqrt{2}\) = 2\(\sqrt{2}\) ≠ 0
अत: (x + 1), बहुपद p(x) का गुणनखण्ड नहीं है।

प्रश्न 2.
गुणनखण्ड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g(x), p(x) का एक गुणनखण्ड है या नहीं :
(i) p(x) = 2x³ + x² – 2x – 1, g(x)= x + 1
(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2
(iii) p(x) = x³ – 4x² + x + 6, g(x) = x – 3.
हल:
(i) यदि g(x) = x + 1, p(x) = 2x³ + x² – 2x -1 का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा
∴ x + 1 = 0 ⇒ x = -1
x के स्थान पर (-1) रखने पर,
p(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= – 2 + 1 + 2 – 1 = 0
∴ g(x), p(x) का गुणनखण्ड है।

(ii) यदि g (x) = x + 2, p(x) = x³ + 3x² + 3x + 1 का गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x + 2 = 0 ⇒ x – 2
x के स्थान पर (-2) रखने पर,
P(-2) = (-2)³ + 3(-2)² + 3(-2) + 1
= – 8 + 12 – 6 + 1 = -1 ≠ 0
∴ g(x), p(x) का गुणनखण्ड नहीं है।

(iii) यह सिद्ध करने के लिए कि g (x) = x – 3, p(x) = x³ – 4x² + x + 6 का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x – 3 = 0
⇒ x = 3
अब, p(3) = (3)³ – 4(3)² + 3 + 6
= 27 – 36 + 3 + 6 = 0
∴ g(x), p(x) का गुणनखण्ड है।

प्रश्न 3.
k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p(x) का एक गुणनखण्ड हो :
(i) p(x) = x + x + k
(ii) p(x) = 2x² + kx + \(\sqrt{2}\)
(iii) p(x) = kx² – \(\sqrt{2}\)x + 1
(iv) p(x) = kx² – 3x + k
हल:
(i) यदि (x – 1), p(x) = x² + x + k का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x – 1 = 0
⇒ x = 1
∴ P(1) = 1² + 1 + k
⇒ 0 = 2 + k ⇒ k = -2.

(ii) यदि (x – 1), p(x) = 2x² + kx + \(\sqrt{2}\) का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x – 1 = 0
⇒ x = 1
∴ p(1) = 2(1)² + k(1) + \(\sqrt{2}\)
⇒ 0 = 2 + k + \(\sqrt{2}\)
⇒ k = -(2 + \(\sqrt{2}\))

(iii) यदि (x – 1), p(x) = kx² – \(\sqrt{2}\)x + 1 का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x – 1 = 0
⇒ x = 1
∴ p(1) = k(1)² – \(\sqrt{2}\)(1) + 1
⇒ 0 = k – \(\sqrt{2}\) + 1
k= \(\sqrt{2}\) – 1.

(iv) यदि (x – 1), p(x) = kx² – 3x + k का एक गुणनखण्ड है, तो भाग देने पर शेषफल शून्य होगा।
∴ x – 1 = 0
⇒ x = 1
∴ p(1) = k(1)² – 3(1) + k
⇒ 0 = k – 3 + k
⇒ 2k = 3
k = \(\frac{3}{2}\)

प्रश्न 4.
गुणनखण्ड ज्ञात कीजिए :
(i) 12x² – 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x – 6
(iv) 3x² – x – 4.
हल:
(i) 12x² – 7x + 1
= 12x² – 4x – 3x + 1
= 4x(3x – 1) -1 (3x – 1)
= (4x – 1) (3x – 1).

(ii) 2x² + 7x + 3
= 2x² + x + 6x + 3
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3).

(iii) 6x² + 5x – 6
= 6x² + 9x – 4x – 6
= 3x(2x + 3) – 2(2x + 3)
= (2x + 3)(3x – 2).

(iv) 3x² – x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4)
= (3x – 4) (x + 1).

प्रश्न 5.
गुणनखण्ड ज्ञात कीजिए :
(i) x³ – 2x² – x + 2
(ii) x³ – 3x² – 9x – 5
(iii) x³ + 13x² + 32x + 20
(iv) 2y³ + y² – 2y – 1.
हल:
(i) माना f(x) = x³ – 2x² – x + 2
स्थिरांक + 2 के गुणनखण्ड 1, 2 हैं।
x – 1 रखने पर, f(1) = 1³ – 2(1)² – 1 + 2
= 1 – 2 – 1 + 2 = 0
x = 1 रखने पर व्यंजक का मान शून्य हो जाता है।
अतः (x – 1), f(x) एक गुणनखण्ड है।
= x³ – 2x² – x + 2
= x²(x – 1) – x² + x – 2x + 2
= x²(x – 1) – x(x – 1) – 2(x – 1)
= (x – 1)(x² – x – 2)
= (x – 1) [(x² + x – 2x – 2)]
= (x – 1) [x(x + 1) – 2(x + 1)]
= (x – 1)(x + 1)(x – 2)

(ii) माना p(x) = x³ – 3x² – 9x – 5
-5 के सभी गुणनखण्ड ±1, ±5 हो सकते हैं।
x = -1 रखने पर,
p(-1) = (-1)³ – 3(-1)² – 9(-1) – 5
= – 1 – 3 + 9 – 5
∴ p(-1) = 0
अत: (x + 1), p(x) का एक गुणनखण्ड है।
x³ – 3x² – 9x – 5
= x³ + x² – 4x² – 9x – 5
= x²(x + 1) – 4x² – 4x – 5x – 5
= x²(x + 1) – 4x(x + 1) – 5(x + 1)
= (x + 1)(x² – 4x – 5)
= (x + 1) [x² + x – 5x – 5]
= (x + 1)[x(x + 1) – 5(x + 1)]
= (x + 1)(x + 1)(x – 5)

(iii) माना p(x) = x³ + 13x² + 32x + 20
+ 20 के गुणनखण्ड हैं।
±1, ±2, ±4, ±5, ±10, तथा ± 20.
x का मान -2 रखने पर पाते हैं :
p(-2) = (-2)³ + 13(-2)² + 32(-2) + 20
= – 8 + 52 – 64 + 20 = 0
∴ (x + 2), p(x) का एक गुणनखण्ड है।
x³ + 13x² + 32x + 20
= x³ + 2x² + 11x² + 32x + 20
= x²(x + 2) + 11x² + 22x + 10x + 20
= x²(x + 2) + 11x(x + 2) + 10(x + 2)
= (x + 2) (x² + 11x + 10)
= (x + 2) (x² + x + 10x + 10)
= (x + 2)[x(x + 1) + 10(x + 1)]
= (x + 2)(x + 1)(x + 10).

(iv) माना p(y) = 2y³ + y² – 2y – 1
-1 के सभी गुणनखण्ड ±1 हैं।
व्यंजक में y का मान रखने पर,
p(1) = 2(1)³ + (1)² – 2(1) – 1
= 2 + 1 – 2 – 1 = 0
अतः (y – 1), p(y) का एक गुणनखण्ड है।
अब y – 1 का P(y) में भाग देने पर,

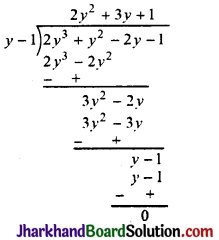
∴ p(y) = (y – 1) (2y² + 3y + 1)
= (y – 1) (2y² + 2y + y + 1)
= (y – 1) [2y(y + 1) + 1(y + 1)]
= (y – 1) (y + 1) (2y + 1).