Jharkhand Board JAC Class 9 Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Exercise 4.4
प्रश्न 1.
समीकरण के रूप में y = 3 का ज्यामितीय निरूपण कीजिए:
(i) एक चर वाले
(ii) दो चर वाले।
हल:
(i) y = 3 समीकरण का ग्राफ पेपर पर निरूपण करने पर x के समान्तर एक सरल रेखा प्राप्त होती है।
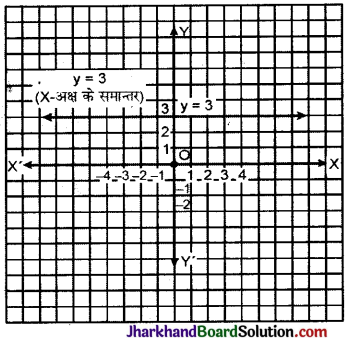
(ii) y = 3 को 0.x + 1.y = 3 के रूप में लिखा जा सकता है।
x के विभिन्न मान रखने पर y = 3 आयेगा। क्योंकि किसी संख्या में शून्य का गुणनफल शून्य होता है
यदि x = 0 हो, तो 0 × 0 + 1.y = 3 ∴ y = 3
यदि x = 2 हो, तो 0 + y = 3 ∴ y = 3
यदि x = 0 हो, तो 0 + y = 3 ∴ y = 3
सारणी:
| x | 0 | 2 | -2 |
| y | 3 | 3 | 3 |
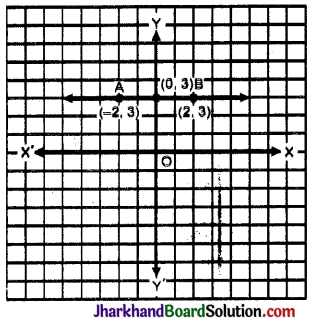
बिन्दुओं (0, 3), (2, 3) और (-2, 3) को निरूपित करने तथा उनको मिलाने पर हमें AB ग्राफ प्राप्त होता है, जो X- अक्ष के समान्तर है तथा उससे 3 इकाई ऊपर की दूरी पर है।
![]()
प्रश्न 2.
समीकरण के रूप में 2x + 9 = 0 का ज्यामितीय निरूपण कीजिए:
(i) एक चर वाले,
(ii) दो चर वाले।
हल:
(i) 2x + 9 = 0 अर्थात् x = \(-\frac{9}{2}\) ग्राफ पेपर पर प्रदर्शित करने से मूलबिन्दु से बायीं तरफ \(-\frac{9}{2}\) इकाई की दूरी पर Y अक्ष के समान्तर रेखा प्राप्त होती है
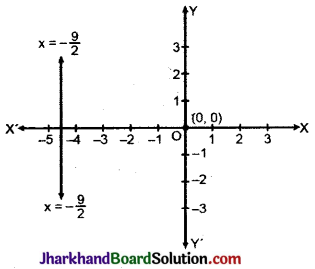
अतः x = \(-\frac{9}{2}\)
(ii) 2x + 9 = 0 को 2x + 0.y + 9 = 0 के रूप में भी लिखा जा सकता है।
y के प्रत्येक मान के लिए x = \(-\frac{9}{2}\) ही प्राप्त होता है।
y के विभिन्न मान लेने पर,
x = \(-\frac{9}{2}\), y = 0, x = \(-\frac{9}{2}\), y = 2
और x = \(-\frac{9}{2}\), y = -2
सारणी :
| x | -9/2 | -9/2 | -9/2 |
| y | 0 | 2 | -2 |
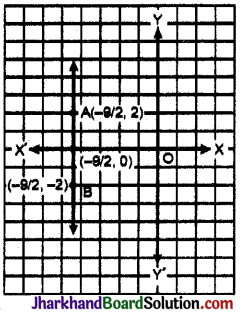
बिन्दुओं \(\left(-\frac{9}{2}, 0\right),\left(-\frac{9}{2}, 2\right),\left(-\frac{9}{2},-2\right)\) ग्राफ पेपर पर निरूपित करके मिलाने पर आलेख AB; Y-अक्ष के समान्तर बायीं ओर \(\frac{9}{2}\) की दूरी पर प्राप्त होता है।