Jharkhand Board JAC Class 9 Maths Solutions Chapter 6 रेखाएँ और कोण Ex 6.3 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 6 रेखाएँ और कोण Exercise 6.3
प्रश्न 1.
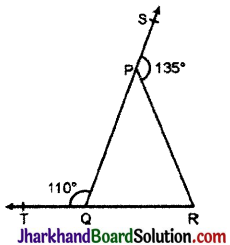
आकृति में, ΔPQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S तथा 7 तक बढ़ाया गया है। यदि ∠SPR = 135° और ∠PQT = 110° हो, तो ∠PRQ ज्ञात कीजिए।
हल:
∠QPR + ∠SPR = 180° [रैखिक युग्म]
⇒ ∠QPR + 135° = 180°
∴ ∠QPR = 180° – 135° = 45°
अब ∠TQP = ∠QPR + ∠PRQ [बहिष्कोण]
⇒ 110° = 45° + ∠PRQ
∴ ∠PRQ = 110° – 45° = 65°
अतः ∠PRQ = 65°
![]()
प्रश्न 2.
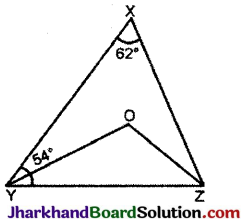
आकृति में, ΔXYZ के ∠X = 62° और ∠XYZ = 54° है। यदि YO और ZO क्रमश: ∠XYZ और ∠XZY के समद्विभाजक हैं, तो ∠OZY और ∠YOZ ज्ञात कीजिए।
हल:
ΔXYZ में
∠YXZ + ∠XYZ + ∠XZY = 180°
[त्रिभुज के अन्तः कोणों का योग]
⇒ 62° + 54° + ∠XZY = 180°
⇒ ∠XZY = 180° – 62° – 54° = 64°
चूँकि YO तथा OZ, ∠XYZ तथा ∠XZY के कोण समद्विभाजक हैं, इसलिए
∠OYZ = \(\frac{1}{2}\)∠XYZ
= \(\frac{1}{2}\) × 54° = 27°
तथा ∠OZY = \(\frac{1}{2}\)∠XZY
= \(\frac{1}{2}\) × 64° = 32°
ΔOYZ में, ∠YOZ + ∠OYZ + ∠OZY = 180°
[त्रिभुज के अन्तः कोणों का योग |
⇒ ∠YOZ + 27° + 32° = 180°
⇒ ∠YOZ = 180° – 27° – 32° = 121°
अत: ∠OZY = 32° तथा ∠YOZ = 121°.
प्रश्न 3.
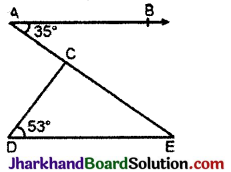
आकृति में यदि AB || DE, ∠BAC = 35° और ∠CDE = 53° है, तो ∠DCE ज्ञात कीजिए।
हल:
दिया है ΔCDE में ∠CDE = 53° तथा ∠BAC = 35°, चूँकि AB || DE तथा तिर्यक रेखा AE उनको क्रमश: A तथा E पर काटती है।
∴ ∠DEA = ∠BAE [एकान्तर कोण]
⇒ ∠DEC = 35°
ΔDEC में,
∠DCE + ∠DEC + ∠CDE = 180°
[Δ के तीनों अन्त: कोणों का योग]
⇒ ∠DCE + 35° + 53° = 180°
⇒ ∠DCE = 180° – 35° – 53° = 92°
∴ ∠DCE = 92°.
![]()
प्रश्न 4.
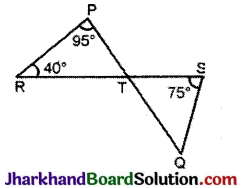
आकृति में, यदि रेखाएँ PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती हैं कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75° है, तो ∠SQT ज्ञात कीजिए।
हल:
ΔPRT में,
∠PRT + ∠RTP + ∠TPR = 180° [Δ के तीनों अन्तःकोण का योग |
⇒ 40° + ∠RTP + 95° = 180°
⇒ ∠RTP = 180° – 40° – 95° = 45°
∠STQ = ∠RTP [शीषांभिमुख कोण]
⇒ ∠STQ = 45°
ΔTQS में,
∠SQT + ∠STQ + ∠TSQ = 180°
[Δ के तीनों अन्तःकोणों का योग |
⇒ ∠SQT + 45° + 75° = 180° [∵ STQ – 45° ]
∴ ∠SQT = 180° – 45° – 75°
⇒ ∠SQT = 60°.
→
प्रश्न 5.
आकृति में, यदि PQ ⊥ PS, PQ || SR, ∠SQR = 28° और ∠QRT = 65° है, तो x और का मान ज्ञात कीजिए।
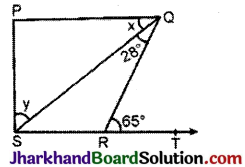
हल:
ΔSRQ में ∠RQS = 28° तथा बहिष्कोण ∠QRT = 65°, बहिष्कोण प्रमेय गुण का उपयोग करते हुए,
∠QRT = ∠RQS + ∠QSR (बहिष्कोण)
⇒ 65° = 28° + ∠QSR
∴ ∠QSR = 65° – 28° = 37°
∵ PQ || SR तथा तिर्यक रेखा PS उनको क्रमशः
P तथा S पर काटती है।
∴ ∠PQS = ∠QSR (एकान्तर कोण)
∠x = 37°
भुजा PQ ⊥ SR
∴ ∠PSQ + ∠QSR = 90°
∠y + 37° = 90°
∠y = 90° – 37
∠y = 53°
![]()
प्रश्न 6.
आकृति में, ΔPQR की भुजा QR को बिन्दु S तक बढ़ाया गया है। यदि ∠PQR और ∠PRS के समद्विभाजक, बिन्दु T पर मिलते हैं, तो सिद्ध कीजिए कि ∠QTR = \(\frac{1}{2}\)∠QPR है।
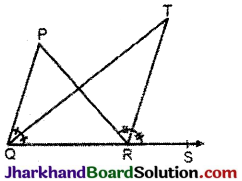
हल:
ΔPQR में, ∠PRS = ∠P + ∠Q (बहिष्कोण)
⇒ \(\frac{1}{2}\)बहिष्कोण बाह्य PRS = \(\frac{1}{2}\)∠P + \(\frac{1}{2}\)∠Q
⇒ ∠TRS = \(\frac{1}{2}\)∠P + ∠TQR ….. (1)
[∵ QT तथा RT क्रमशः ∠Q तथा ∠PRS के कोण समद्विभाजक हैं।
∴ ∠Q = 2∠TQR तथा बाह्य ∠PRS = 2∠TRS]
ΔQRT में, बाह्य ∠TRS = ∠TQR + ∠T ….. (2)
(1) तथा (2) से,
\(\frac{1}{2}\)∠P + ∠TQR = ∠TQR + ∠T
\(\frac{1}{2}\)∠P = ∠T
∠QTR = \(\frac{1}{2}\)∠QPR. इति सिद्धम्।