Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 Triangles Ex 7.2 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.2
Page-123
Question 1.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that:
(i) OB = OC
(ii) AO bisects ∠A
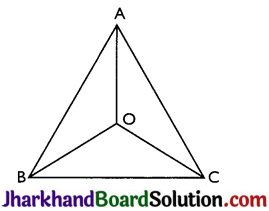
Answer:
Given: AB = AC, the bisectors of ∠B and ∠C intersect each other at O.
Proof:
(i) Since ABC is an isosceles with AB = AC,
∴ ∠B = ∠C (Angles opposite to equal sides are equal)
⇒ \(\frac{1}{2}\)∠B = \(\frac{1}{2}\)∠C (As OB and OC bisects ∠B and ∠C)
⇒ ∠OBC = ∠OCB (Angle bisectors)
⇒ OB = OC (Sides opposite to the equal angles are equal)
(ii) In ΔABO and ΔAOC,
AB = AC (Given)
AO = AO (Common)
OB = OC (Proved above)
Therefore, ΔABO ≅ ΔACO by SSS congruence criterion.
∠BAO = ∠CAO (by CPCT)
Thus, AO bisects ∠A.
![]()
Question 2.
In ΔABC, AD is the perpendicular bisector of BC (see Fig). Show that ΔABC is an isosceles triangle in which AB = AC.
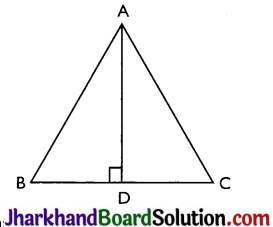
Answer:
Given: AD is the perpendicular bisector of BC
To prove: AB = AC
Proof: In ΔADB and ΔADC,
AD = AD (Common)
∠ADB = ∠ADC = 90° (AD ⊥ BC)
BD = CD (AD bisects BC)
Therefore, ΔADB ≅ ΔADC by SAS congruence criterion.
AB = AC (by CPCT)
∴ AABC is an isosceles triangle.
Page-124
Question 3.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig). Show that these altitudes are equal.
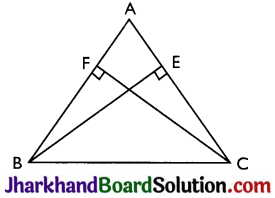
Answer:
Given BE and CF are altitudes.
To prove: BE = CF
Proof: In ΔAEB and ΔAFC,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
Therefore, ΔAEB ≅ ΔAFC by AAS congruence criterion.
Thus, BE = CF (CPCT)
Question 4.
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig). Show that
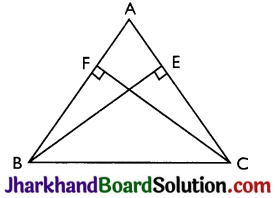
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
Answer:
Given: BE = CF
Proof: (i) In ΔABE and ΔACF,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
BE = CF (Given)
Therefore, ΔABE ≅ ΔACF by AAS congruence criterion.
(ii) Thus, AB = AC by CPCT and therefore, ABC is an isosceles triangle.
![]()
Question 5.
ABC and DBC are two isosceles triangles on the same base BC (see Fig). Show that ∠ABD = ∠ACD.
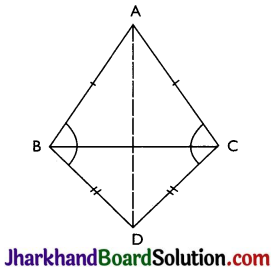
Answer:
Given: ABC and DBC are two isosceles triangles.
To prove: ∠ABD = ∠ACD
Proof: In ΔABD and ΔACD,
AD = AD (Common)
AB = AC (ABC is an isosceles triangle)
BD = CD (BCD is an isosceles triangle)
Therefore, ΔABD ≅ ΔACD by SSS congruence criterion.
Thus, ∠ABD = ∠ACD (CPCT)
Question 6.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig). Show that ∠BCD is a right angle.
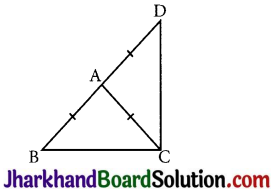
Answer:
Given: AB = AC and AD = AB
To prove: ∠BCD is a right angle.
Proof: In ΔABC,
AB = AC (Given)
AB = AD (Given)
∴ AC = AD …(i)
AB = AC (Given)
⇒ ∠ACB = ∠ABC (Angles opposite to the equal sides are equal.)
In ΔACD,
AD = AC (From (i))
⇒ ∠ADC = ∠ACD (Angles opposite to the equal sides are equal.)
In ΔBCD, ∠B + ∠C + ∠D = 180°
⇒ ∠B + (∠BCA + ∠DCA) + ∠D = 180°
⇒ 2 ∠BCA + 2 ∠ACD = 180°
(∵∠ACB = ∠ABC and ∠ADC = ∠ACD)
⇒ ∠BCA + ∠ACD = 90°
⇒ ∠BCD = 90°.
![]()
Question 7.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
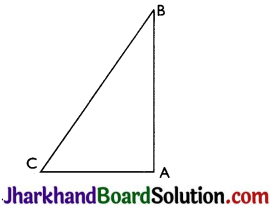
Answer:
Given: ∠A = 90° and AB = AC
Proof: AB = AC
⇒ ∠C = ∠B (Angles opposite to the equal sides are equal)
Now, ∠A + ∠B + ∠C = 180° (Sum of the interior angles of the triangle)
⇒ 90° + 2∠B = 180° (∵∠B = ∠C)
⇒ 2∠B = 90°
⇒ ∠B = 45°
Thus, ∠B = ∠C = 45°
Question 8.
Show that the angles of an equilateral triangle are 60° each.
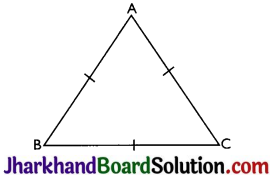
Answer:
Let ABC be an equilateral triangle.
BC = AC = AB (Length of all sides in an equilateral triangle is same)
⇒ ∠A = ∠B = ∠C (Sides opposite to the equal angles are equal)
Also, ∠A + ∠B + ∠C = 180°
⇒ 3∠A = 180°
⇒ ∠A = 60°
Therefore, ∠A = ∠B = ∠C = 60°
Thus, the angles of an equilateral triangle are 60° each.