Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.4 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Exercise 9.4
प्रश्न 1.
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
हल:
दिया है एक समान्तर चतुर्भुज ABCD और एक आयत ABEF समान आधार पर स्थित हैं और उनके क्षेत्रफल भी समान हैं।
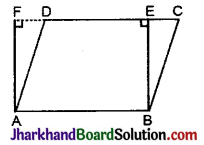
सिद्ध करना है: समान्तर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।
उपपत्ति: ∵ समान्तर चतुर्भुज और आयत की सम्मुख भुजाएँ बराबर होती हैं।
∴ AB = DC …..(i)
[∵ ABCD एक समान्तर चतुर्भुज है]
तथा AB = EF …..(ii)
समीकरण (i) व (ii) से,
DC = EF [∵ ABEF एक आयत है।]
दोनों ओर AB को जोड़ने पर,
AB + DC = AB + EF ….. (iii)
∵ दी गई रेखा के किसी बिन्दु से खींचे जा सकने वाले सभी रेखा खण्ड इस पर स्थित नहीं है, अतः लम्ब खण्ड सबसे छोटा है।
∴ BE < BC तथा AF < AD
⇒ BC > BE तथा AD > AF
⇒ BC + AD > BE + AF …..(iv)
समीकरण (iii) व (iv) को जोड़ने पर
AB + DC + BC + AD > AB + EF + BE + AF
⇒ AB + BC + CD + DA > AB + BE + EF + FA
अत: समान्तर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।
इति सिद्धम्।
![]()
प्रश्न 2.
आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD = DE = EC है दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है। क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है ?”
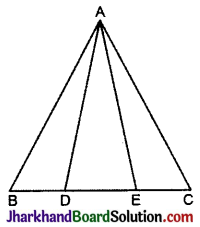
हल:
माना AL रेखा BC पर लम्ब है, अत: AL, ΔABD, ΔADE और ΔAEC की ऊँचाई है।
∴ ar (ΔABD) = \(\frac{1}{2}\) × BD × AL
ar (ΔADE) = \(\frac{1}{2}\) × DE × AL
और ar (ΔAEC) = \(\frac{1}{2}\) × EC × AL
⇒ BD = DE = EC
∴ ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
हाँ, सभी त्रिभुजों की ऊँचाई समान है। बुधिया इस उत्तर द्वारा अपने खेत को तीन बराबर भागों में बाँट सकती है।
प्रश्न 3.
आकृति में ABCD, DCFE और ABFE समान्तर चतुर्भुज हैं। दर्शाइए कि ar (ΔADE) = ar (ΔBCF)।
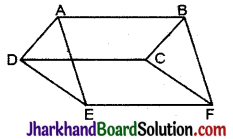
हल:
चूँकि समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं। और ☐ABCD, ☐DCEF तथा ☐ABFE समान्तर चतुर्भुज हैं।
∴ AD = BC
इसी प्रकार, DE = CF
और AE = BF
ΔADE ≅ ΔBCF (SSS नियम)
या ar (ΔADE) = ar (ΔBCF). इति सिद्धम्।
![]()
प्रश्न 4.
आकृति में, ABCD एक समान्तर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि
ar (ΔBPC) = ar (ΔDPQ).
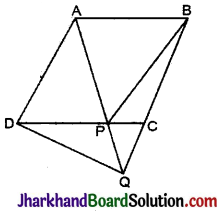
हल:
A और C को मिलाया।
∵ ΔAPC और ΔBPC एक ही आधार PC पर तथा समान समान्तर रेखाओं PC और AB के मध्य स्थित हैं।
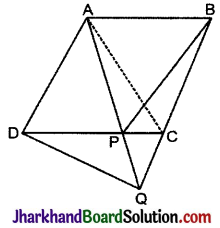
∴ ar (ΔAPC) = ar (ΔBPC) …..(i)
∵ AD = CQ (दिया है)
∵ AD || BC (∵ ABCD समान्तर चतुर्भुज है)
तथा AD || CQ
∴ चतुर्भुज ADQC में, सम्मुख भुजाओं का एक युग्म बराबर और समान्तर है।
∴ ADQC एक समान्तर चतुर्भुज है।
⇒ AP = PQ और CP = DP
[∵ समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं]
ΔAPC और ΔDPQ में,
∵ AP = PQ
∠APC = ∠DPQ [ऊर्ध्वाधर सम्मुख कोण हैं]
PC = PD [सिद्ध किया है]
∴ ΔAPC ≅ ΔDPQ (SAS नियम)
⇒ ar (ΔAPC) = ar (ΔDPQ)
∴ ar (ΔBPC) = ar (ΔDPQ), [∵ ar (ΔAPC) = ar (ΔBPC)] इति सिद्धम्।
प्रश्न 5.
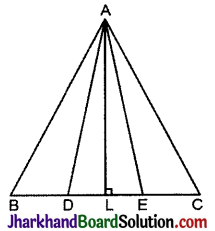
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेदित करती है, तो दर्शाइए कि
(i) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE)
(iii) ar (ΔABC) = 2ar(ΔBEC)
(iv) ar (ΔBFE) = ar (ΔAFD)
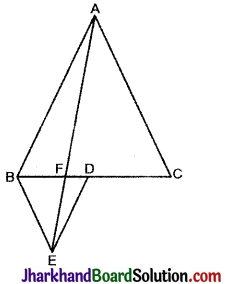
(v) ar (ΔBFE) = 2 ar (ΔFED).
(vi) ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
हल:
दिया है दी गई आकृति ABC और ABDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्यबिन्दु है। रेखाखण्ड AE खींचा गया है जो BC को F पर प्रतिच्छेदित करता है।
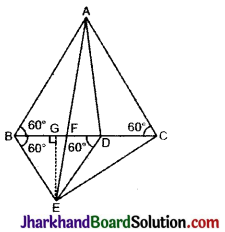
सिद्ध करना है:
(i) ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
(ii) ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE)
(iii) ar (ΔABC) = 2ar(ΔBEC)
(iv) ar (ΔBFE) = ar (ΔAFD)
(v) ar (ΔBFE) = 2 ar (ΔFED).
(vi) ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
रचना: रेखाखण्ड EC और AD खींचे।
उपपत्ति: (i) ∵ D, BC का मध्य- बिन्दु है।
∴ BD = DC या BD = \(\frac{1}{2}\)BC

तब समीकरण (1) व (2) से,
ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC).
(ii) ∵ ΔABC समबाहु त्रिभुज है।
∴ ∠ACB = 60°
और ΔBDE समबाहु त्रिभुज है।
∴ ∠DBE = 60° या ∠CBE = 60°
∴ ∠ACB और ∠CBE एकान्तर कोण हैं जो BE तथा AC को BC द्वारा काटने से बने हैं।
∴ BE || AC
∵ ΔBAE और ΔBEC समान आधार BE पर और समान समान्तर रेखाओं BE AC के मध्य स्थित हैं।
∴ ar (ΔBAE) = ar (ΔBEC) ……(3)
∵ D, BC का मध्यबिन्दु है।
∴ DE, ΔBEC की माध्यिका है।
∴ ar (ΔBDE) = ar (ΔDEC)
⇒ ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBEC)
⇒ 2ar (ΔBDE) = ar (ΔBEC) ……(4)
समीकरण (3) व (4) से,
2 ar (ΔBDE) = ar (ΔBAE)
अतः ar (ΔBDE) = \(\frac{1}{2}\)ar (ΔBAE).
(iii) समीकरण (4) से,
2 ar (ΔBDE) = ar (ΔBEC)
परन्तु परिणाम (i) से,
ar (ΔBDE) = \(\frac{1}{4}\)ar (ΔABC)
∴ 2 · \(\frac{1}{4}\) ar (ΔABC) = ar (ΔBEC)
या \(\frac{1}{2}\) ar (ΔABC) = ar (ΔBEC)
अत: \(\frac{1}{2}\) ar (ΔABC) = 2 ar (ΔBEC)
(iv) ∵ ΔBDE समबाहु त्रिभुज है।
∴ ∠BDE = 60°
और ΔABC समबाहु त्रिभुज है।
∴ ∠ABC = 60° या ∠ABD = 60°
∵ ∠BDE और ∠ABD एकान्तर कोण हैं जो AB और DE को BD के काटने से बने हैं।
∴ AB || DE
∵ ΔBDE और ΔADE एक ही आधार DE पर और समान समान्तर रेखाओं AB और DE के बीच बने हैं।
∴ ar (ΔBDE) = ar (ΔADE)
ar (ΔBFE) + ar (ΔFED) = ar (ΔFED) + ar (ΔAFD)
या ar (ΔBFE) = ar (ΔAFD).
(v) ∵ ΔABC की भुजा ΔBDE की भुजा से दो गुनी है।
∴ ΔABC की ऊँचाई भी ΔBDE की ऊँचाई से दो गुनी होगी।
∴ GE : AD = 1 : 2
यही अनुपात GF और FD में भी होगा, अत:
GF : FD = 1 : 2
परन्तु GD = BG = \(\frac{1}{4}\)BC
परन्तु GD = GF + FD
यदि GF = a तो FD = 2a होगा।
तब GD = a + 2a = 3a
तब BC = 2BD = 2(2BG)
= 4GB = 4GD = 4 × 3a = 12a
BG = GD = 3a ⇒ BD = 6a
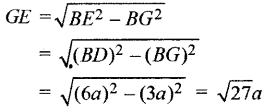

(vi) ∵ परिणाम (iv) से,
ar (ΔAFD) = ar (ΔBFE)
और परिणाम (v) से,
ar (ΔBFE) = 2 ar (ΔFED)
∴ ar (ΔAFD) = 2ar (ΔFED) ……(5)
∵ ar (ΔACD)= \(\frac{1}{2}\)ar (ΔABC)
= \(\frac{1}{2}\) · 4 ar (ΔBDE), परिणाम (i) से
= 2 ar (ΔBDE)
∴ ar (ΔACD) = 2 ar (ΔBDE) …..(6)
∵ ar (ΔBFE) = 2ar (ΔFED), परिणाम (v) से
दोनों ओर ar (ΔFED) जोड़ने पर,
ar (ΔBFE) + ar (ΔFED) = 3 ar (ΔFED)
या ar (ΔBDE) = 3 ar (ΔFED) …..(7)
समीकरण (6) व (7) से,
ar (ΔACD) = 2[3 ar (ΔFED)]
∴ ar (ΔACD) = 6ar (ΔFED) …..(8)
समीकरण (5) व (8) को जोड़ने पर,
ar (ΔAFD) + ar (ΔACD) = 8 ar (ΔFED)
∴ ar (ΔAFC) = 8 ar (ΔFED)
अतः ar (ΔFED) = \(\frac{1}{8}\)ar (ΔAFC).
इति सिद्धम्।
![]()
प्रश्न 6.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु पर प्रतिच्छेदित करते हैं दर्शाइए कि
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC) है।
हल:
दिया है: ☐ABCD के विकर्ण AC और BD परस्पर बिन्दु पर प्रतिच्छेदित करते हैं।
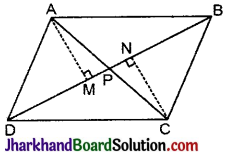
सिद्ध करना है:
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)
रचना : A तथा C से BD पर क्रमश: AM तथा CN लम्ब डालें।
उपपत्ति: ar (ΔAPB) = \(\frac{1}{2}\)AM × BP …..(1)
ar (ΔAPD) = \(\frac{1}{2}\)AM × DP …..(2)
ar (ΔBPC) = \(\frac{1}{2}\)CN × BP …(3)
ar (ΔCPD) = \(\frac{1}{2}\)CN × DP ….. (4)
समीकरण (1) को (2) से भाग देने पर,

वज्रगुणन से,
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC). इति सिद्धम्।
प्रश्न 7.
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिन्दु हैं तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि
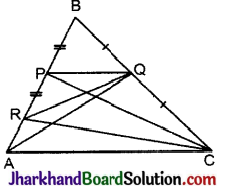
(i) ar (ΔPRQ) = \(\frac{1}{2}\)ar (ΔARC)
(ii) ar (ΔRQC) = \(\frac{3}{8}\)ar (ΔABC)
(iii) ar (ΔPBQ) = ar (ΔARC).
हल:
P और Q क्रमश: त्रिभुज ABC की भुजाओं AB और BC के मध्य बिन्दु हैं। AQ और PC को मिलाया।
(i) ∵ ar (ΔPQR) = \(\frac{1}{2}\)ar (ΔAPQ),
[∵ QR, त्रिभुज APQ की माध्यिका है जो इसे समान क्षेत्रफलों वाले त्रिभुजों में बाँटती है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABQ)
[∵ QP, त्रिभुज ABQ की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABQ)
= \(\frac{1}{4} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, त्रिभुज ABC की माध्यिका है]
= \(\frac{1}{8}\)ar (ΔABC) …..(i)
पुन:, ar (ΔARC) = \(\frac{1}{2}\)ar (ΔAPC)
[∵ CR, त्रिभुज APC की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC)
[∵ CP त्रिभुज ABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC) ……(ii)
समीकरण (i) और (ii) से,
ar (ΔPQR) = \(\frac{1}{8}\)ar (ΔABC)
= \(\frac{1}{2} \times \frac{1}{4}\)ar (ΔABC)
[∵ \(\frac{1}{4}\)ar (ΔABC) = ar (ΔARC)]
= \(\frac{1}{2}\)ar (ΔARC). इति सिद्धम्।
(ii) ar (ΔRQC) = ar (ΔRQA) + ar (ΔAQC) – ar (ΔARC) …..(iii)
अब ar (ΔRQA) = \(\frac{1}{2}\)ar (ΔPQA)
[∵ RQ, ΔPQA की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔAQB)
[∵ AQ, ΔAQB की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔAQB)
= \(\frac{1}{4} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, ΔABC की माध्यिका है]
= \(\frac{1}{8}\)ar (ΔABC) …..(iv)
अतः ar (ΔAQC) = \(\frac{1}{2}\)ar (ΔABC) …..(v)
[∵ AQ, ΔABC की माध्यिका है]
⇒ ar(ΔARC) = \(\frac{1}{2}\)ar (ΔAPC)
[∵ CR, ΔAPC की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar(ΔABC)
[∵ CP, ΔABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC) …..(vi)
समीकरण (iii), (iv), (v) और (vi) से,
ar (ΔRQC) = \(\frac{1}{8}\)ar (ΔABC) + \(\frac{1}{2}\)ar (ΔABC) – \(\frac{1}{4}\)ar (ΔABC)
= \(\left(\frac{1}{8}+\frac{1}{2}-\frac{1}{4}\right)\)ar (ΔABC)
= \(\frac{3}{8}\)ar (ABC).
इति सिद्धम्।
(iii) ∵ ar (ΔPBQ) = ar (ΔABQ)
[∵ PQ, ΔABQ की माध्यिका है]
= \(\frac{1}{2} \times \frac{1}{2}\)ar (ΔABC)
[∵ AQ, ΔABC की माध्यिका है]
= \(\frac{1}{4}\)ar (ΔABC)
= ar (ΔARC) [समीकरण (vi) से]
इति सिद्धम्।
![]()
प्रश्न 8.
आकृति में, ABC एक समकोण त्रिभुज है, जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखण्ड AX ⊥ DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि
(i) ΔMBC ≅ ΔABD
(ii) ar (☐BYXD) = 2 ar (ΔMBC)
(iii) ar (☐BYXD) = ar (☐ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar (☐CYXE) = 2 ar (ΔFCB)
(vi) ar (☐CYXE) = ar (☐ACFG)
(vii) ar (☐BCED) = ar (☐ABMN) + ar (ACFG).
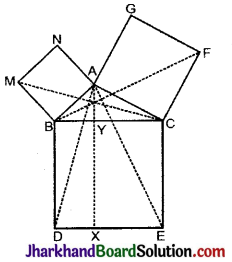
हल:
(i) ΔMBC और ΔABD में,
∵ BC = BD [वर्ग BCED की भुजाएँ]
MB = AB [वर्ग ABMN की भुजाएँ]
∠MBC = ∠ABD
[∵ प्रत्येक कोण = 90° + ∠ABC] (SAS नियम)
ΔMBC ≅ ΔABD. इति सिद्धम्।
(ii) ΔABD और आयत BYXD समान आधार BD पर और समान समान्तर रेखाओं BD और XY के मध्य स्थित हैं।
∴ ar (ΔABD) = \(\frac{1}{2}\)ar (☐BYXD)
लेकिन ΔMBC = ΔABD [भाग (i) से]
⇒ ar (ΔMBC) = ar (ΔABD)
∴ ar (ΔMBC) = ar (ΔABD)
= \(\frac{1}{2}\)ar (☐BYXD)
⇒ ar (☐BYXD) = 2ar (ΔMBC). इति सिद्धम्।
(iii) वर्ग ABMN और ΔMBC समान आधार MB पर और समान समान्तर रेखाओं MB और NAC के बीच स्थित हैं।
∴ ar (ΔMBC) = \(\frac{1}{2}\)ar(☐ABMN)
ar (☐ABMN) = 2 ar (ΔMBC)
ar (☐ABMN) = ar (☐BYXD). [भाग (ii) से]
इति सिद्धम्।
(iv) ΔACE और ΔBCF में,
CE = BC [वर्ग BCED की भुजाएँ]
AC = CF [वर्ग ACFG की भुजाएँ]
और ∠ACE = ∠BCF [∵ प्रत्येक 90° + ∠BCA]
∴ ΔACE ≅ ΔBCF. (SAS नियम) इति सिद्धम्।
(v) ΔACE और आयत CYXE समान आधार CE पर और समान समान्तर रेखाओं CE और AYX के बीच स्थित हैं।
ar (ΔACE) = \(\frac{1}{2}\)ar (☐CYXE)
⇒ ar (ΔFCB) = \(\frac{1}{2}\)ar (☐CYXE)
[∵ ΔACE ≅ ΔBCF, भाग (iv) से]
⇒ ar (☐CYXE) = 2ar (ΔFCB). इति सिद्धम्।
(vi) वर्ग ACFG और ΔBCF समान आधार CF पर और समान समान्तर रेखाओं CF और BAG के मध्य स्थित हैं।
∴ ar (ΔBCF) = \(\frac{1}{2}\)ar (☐ACFG)
⇒ \(\frac{1}{2}\)ar (☐CYXE) = \(\frac{1}{2}\)ar (☐ACFG) [भाग (v) से]
⇒ ar (☐CYXE) = ar (☐ACFG). इति सिद्धम्।
(vii) भाग (iii) और (vi) से,
ar (☐BYXD) = ar (☐AMBN)
और ar (☐CYXE) = ar (☐ACFG)
जोड़ने पर,
ar (☐BYXD) + ar (☐CYXE) = ar (☐ABMN) + ar (ACFG)
या ar (☐BCED) = ar (☐ABMN) + ar (☐ACFG).
इति सिद्धम्।