JAC Class 9 Science Solutions Chapter 9 बल तथा गति के नियम

Jharkhand Board JAC Class 9 Science Solutions Chapter 9 बल तथा गति के नियम Textbook Exercise Questions and Answers.

JAC Board Class 9 Science Solutions Chapter 9 बल तथा गति के नियम

Jharkhand Board Class 9 Science बल तथा गति के नियम Textbook Questions and Answers

प्रश्न 1.
कोई वस्तु शून्य बाह्य असन्तुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशून्य वेग से गति करना सम्भव है? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख कीजिए। यदि नहीं, तो कारण स्पष्ट कीजिए।
उत्तर:
हाँ, सम्भव है। वास्तव में गति की अवस्था में परिवर्तन के लिए बल की आवश्यकता होती है न कि एकसमान गति की अवस्था को बनाए रखने के लिए। अतः यदि कोई वस्तु पहले से गतिमान है तो वह बाह्य असन्तुलित बल की अनुपस्थिति में भी एकसमान गति की अवस्था को बनाए रखेगी। इस स्थिति में वस्तु के वेग का परिमाण तथा गति की दिशा दोनों नियत रहेंगे।

प्रश्न 2.
जब किसी छड़ी से एक दरी (कार्पेट) को पीटा जाता है तो धूल के कण बाहर आ जाते हैं। स्पष्ट कीजिए।
उत्तर:
दरी (कार्पेट) को छड़ी से पीटने पर धूल के कण निकल आते हैं- इसका कारण यह है कि छड़ी से पीटने पर दरी (कार्पेट) के कण तो गति की अवस्था में आ जाते हैं, परन्तु विराम जड़त्व के कारण धूल के कण विराम में ही बने रहते हैं और दरी (कार्पेट) के कणों से अलग होकर बाहर निकल जाते हैं।

प्रश्न 3.
बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है?
उत्तर:
जब चलती हुई गाड़ी में अचानक ब्रेक लगाए जाते हैं अथवा एकाएक उसे मोड़ा जाता है तो गति जड़त्व के कारण गाड़ी की छत पर रखा सामान उसी वेग से उसी दिशा में गतिमान रहने का प्रयास करता है। ऐसे में यदि सामान को बाँधा नहीं गया है तो वह छत से नीचे गिर सकता है, इससे सामान के टूटने की सम्भावना रहती है। अतः बस की छत पर रखे सामान को बाँधकर रखा जाता है।

प्रश्न 4.
किसी बल्लेबाज द्वारा क्रिकेट की गेंद को मारने पर गेंद जमीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि-
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असन्तुलित बल कार्यरत नहीं है; अतः गेंद विरामावस्था में आने के लिए प्रयासरत है। (सही विकल्प का चयन कीजिए।)
उत्तर:
(c) गेंद पर गति की दिशा में विपरीत एक बल कार्य कर रहा है।

प्रश्न 5.
एक ट्रक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20 सेकण्ड में 400 मीटर की दूरी तय करता है। इसका त्वरण ज्ञात कीजिए। अगर इसका द्रव्यमान 7 टन है तो इस पर लगने वाले बल की गणना कीजिए। (1 टन = 1000 किग्रा)
हल:
प्रश्नानुसार दूरी (s) = 400 मीटर,
प्रारम्भिक वेग (u) = 0 मीटर / सेकण्ड,
समय (t) = 20 सेकण्ड, त्वरण (a) = ?
s = ut + \(\frac { 1 }{ 2 }\) at² से
400 = (0 × 20) + \(\frac { 1 }{ 2 }\) a × (20)²
अथवा 400 = 200 a
अतः ट्रक का त्वरण (a) = \(\frac { 400 }{ 200 }\) = 2 मीटर/सेकण्ड²।
दिया है त्वरण (a) = 2 मीटर / सेकण्ड², द्रव्यमान (m) = 7 टन 7000 किग्रा, बल (F) = ?
सूत्र
F = m x a से,
बल (F) = 7000 किग्रा x 2 मीटर/सेकण्डर
= 14,000 किग्रा मीटर/सेकण्डर
= 14,000 न्यूटन
अतः ट्रक पर लगा बल = 14,000 न्यूटन।

प्रश्न 6.
1 किग्रा द्रव्यमान के एक पत्थर को 20 मीटर / सेकण्ड के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 मीटर की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना कीजिए।
हल
दिया है द्रव्यमान m = 1 किग्रा, 4 = 20 मीटर / सेकण्ड s = 50 मीटर, v = 0 मीटर / सेकण्ड, बल F = ?
सूत्र,
v² – u² = 2as से,
0² – (20)² = 2a × 50
या a = – \(\frac{20 \times 20}{2 \times 50}\)
= – 4 मीटर / सेकण्डर
ऋणात्मक चिह्न मन्दन को प्रदर्शित करता है।
अत: पत्थर का मन्दन 4 मीटर / सेकण्ड है।
अब सूत्र F = m xa से,
बर्फ द्वारा पत्थर पर लगाया गया बल
F = 1 किग्रा x 4 मीटर / सेकण्ड² = 4 न्यूटन
अतः बर्फ तथा पत्थर के बीच 4 न्यूटन का बल लगता है।

प्रश्न 7.
एक 8,000 किग्रा द्रव्यमान का रेल इंजन प्रति 2,000 किग्रा द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40,000 न्यूटन का बल आरोपित करता है तथा पटरी 5,000 न्यूटन का घर्षण बल लगाती हो तो ज्ञात कीजिए-
(a) नेट त्वरण बल
(b) रेल का त्वरण
हल:
दिया है इंजन द्वारा लगाया गया बल = 40,000 न्यूटन,
इंजन का द्रव्यमान = 8,000 किग्रा,
पटरी द्वारा लगाया गया घर्षण बल = 5,000 न्यूटन,
प्रत्येक डिब्बे का द्रव्यमान = 2,000 किग्रा।
(a) ∵ घर्षण बल एक अवरोधी बल है,
∴ रेलगाड़ी पर नेट त्वरण बल = इंजन का बल – पटरी का घर्षण बल
= 40,000 – 5,000- 35,000 न्यूटन।

(b) पाँच डिब्बों का कुल द्रव्यमान
m = 5 × 2000 = 10,000 किग्रा
जबकि डिब्बों पर नेट त्वरण बल
F = 35,000 न्यूटन
∴ सूत्र F = ma से,

प्रश्न 8.
एक गाड़ी का द्रव्यमान 1,500 किग्रा है। यदि गाड़ी को 1.7 मीटर / सेकण्ड के ऋणात्मक त्वरण (अव- मन्दन) के साथ विरामावस्था में लाना है तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा?
हल:
दिया है गाड़ी का द्रव्यमान m= 1,500 किग्रा, मन्दन a = 1.7 मीटर/सेकण्डर²
माना कि गाड़ी व सड़क के बीच लगा बल = F
तब यही बल गाड़ी में मन्दन उत्पन्न करेगा; अतः
सूत्र F = m x a से,
बल F = 1,500 किग्रा 1.7 मीटर/सेकण्डर²
= 2,550 न्यूटन।

प्रश्न 9.
किसी द्रव्यमान की वस्तु, जिसका वेग है, का संवेग क्या होगा?
(a) (mv)²
(b) mv²
(c) \(\frac { 1 }{ 2 }\) mv²
(d) mv
(उपर्युक्त में से सही विकल्प चुनिए)
उत्तर:
(d) mv.

प्रश्न 10.
हम एक लकड़ी के बक्से को 200 न्यूटन बल लगाकर उसे नियत वेग से फर्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा?
हल:
बक्से पर लगाया गया बल F₁ = 200 न्यूटन
माना बक्से पर लगा घर्षण बल तब बक्से पर लगा नेट बल = F₂ न्यूटन
= F₁ – F₂ = (200 – F₂) न्यूटन
∵ बक्सा नियत वेग से गतिमान है; अतः बक्से पर नेट असन्तुलित बल शून्य होगा।
अत: नेट बल = (200 – F₂) = 0
F₂ = 200 न्यूटन
अतः बक्से पर लगा घर्षण बल 200 न्यूटन है।

प्रश्न 11.
दो वस्तुएँ, प्रत्येक का द्रव्यमान 1-5 किग्रा है, एक ही सीधी रेखा में एक-दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग 2.5 मीटर / सेकण्ड है। टकराने के बाद यदि दोनों एक-दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा?
हल:
दिया है वस्तुओं के द्रव्यमान m₁ = m₂ = 1.5 किग्रा
टकराने से पहले इनके वेग u₁ = 2.5 मीटर / सेकण्ड
u₂ = 22.5 मीटर / सेकण्ड
(ऋण चिह्न विपरीत दिशा के कारण लिया है।)
माना कि टक्कर के बाद दोनों का सम्मिलित वेग v हो जाता है।
दोनों के जुड़ जाने से बनी नई वस्तु का द्रव्यमान (m₁ + m₂) होगा।
तब टक्कर के पहले दोनों का कुल संवेग
= m₁u₂ + m₂u₂
= 1.5 x 2.5 + 15 x (-2.5)
= 3.75 – 3.75 = 0
तथा टक्कर के बाद दोनों का कुल संवेग
= (m₁ + m₂)v = (1·5 + 1.5) v = 3v
संवेग संरक्षण के नियम से,
टक्कर के बाद कुल संवेग = टक्कर के पहले कुल संवेग
अर्थात्
3v = 0
∴ v = 0
अतः टक्कर के बाद दोनों वस्तुओं का सम्मिलित वेग शून्य होगा अर्थात् वे विरामावस्था में आ जाएँगी।

प्रश्न 12.
गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्तु एक ट्रक है जो सड़क के किनारे खड़ा है; सम्भवतः हमारे द्वारा बल आरोपित करने पर गतिशील नहीं हो पाएगा एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दीजिए और बताइए कि ट्रक गतिशील क्यों नहीं हो पाता?
उत्तर:
विद्यार्थी का तर्क गलत है, यह सही है कि क्रिया तथा प्रतिक्रिया के बल विपरीत एवं बराबर होते हैं, परन्तु ये बल कभी भी एक ही वस्तु पर कार्य नहीं करते। जैसे कि उपर्युक्त उदाहरण में, हमारे द्वारा आरोपित बल ट्रक पर लगेगा, जबकि ट्रक का प्रतिक्रिया बल हम पर लगेगा। ट्रक के गतिमान होने का सम्बन्ध केवल ट्रक पर लगने वाले बल से है न कि हमारे द्वारा लगे प्रतिक्रिया बल से अतः क्रिया-प्रतिक्रिया के बलों के निरस्त होने का यहाँ कोई प्रश्न ही नहीं उठता।

हमारे द्वारा ट्रक पर बल आरोपित किए जाने पर भी ट्रक गतिशील नहीं हो पाता, इसका कारण यह है कि ट्रक पर इस बल के अतिरिक्त पृथ्वी द्वारा आरोपित घर्षण बल भी लगा है। जो कि हमारे द्वारा आरोपित बल को सन्तुलित कर देता है।

प्रश्न 13.
200 ग्राम द्रव्यमान की हॉकी की एक गेंद 10 ms^-1 से गति कर रही है। यह एक हॉकी स्टिक से इस प्रकार टकराती है कि यह 5ms^-1 के वेग से अपने प्रारंभिक मार्ग पर वापस लौटती है। हॉकी स्टिक द्वारा आरोपित बल द्वारा हॉकी की गेंद में आये संवेग परिवर्तन के परिमाप का परिकलन कीजिए।
हल:
दिया है गेंद का द्रव्यमान m = 200 g = 0.2kg
गेंद का प्रारम्भिक वेग, u₁ = 10 m/s
गेंद का प्रारंभिक संवेग = mu₁ = 0.2 x 10 = 2 kg m/s
गेंद का अंतिम वेग, u₂ = – 5 ms^-1
गेंद का अंतिम संवेग = mu₂ x 0.2 x – 5 = – 1 kg m/s
संवेग परिवर्तन = 1 Ns – 2Ns = – 3 kg m/s

प्रश्न 14.
10 ग्राम द्रव्यमान की एक गोली सीधी रेखा में 150 मीटर / सेकण्ड के वेग से चलकर एक लकड़ी के गुटके से टकराती है और 0-03 सेकण्ड के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी? लकड़ी के गुटके द्वारा गोली पर लगाए गए बल के परिमाण की गणना कीजिए।
हल:
दिया है गोली का द्रव्यमान
m = 10 ग्राम
= \(\frac { 10 }{ 1000 }\)
= 0.01
किग्रा, वेग u = 150 मीटर / सेकण्ड
समय t = 0.03 सेकण्ड, वेग v = 0 मीटर/सेकण्ड s = ?
गोली का त्वरण a = \(\frac { v-u }{ t }\)
= \(\frac { 0-150 }{ 0.03 }\)
= – \(\frac { 150 }{ 0.03 }\)
= – 5000 मीटर / सेकण्ड²
ऋणात्मक चिह्न मन्दन को प्रदर्शित करता है।
अब दूरी s = ut + \(\frac { 1 }{ 2 }\) at²
s = 150 × 0.03 + \(\frac { 1 }{ 2 }\) (- 5000) x (0.03)²
= 4.5 – 2500 – 0.0009
= 4.5 – 2.25
= 2.25
अतः गोली लकड़ी को 2.25 मीटर दूरी तक भेदेगी।
पुन: सूत्र F = ma से,
लकड़ी द्वारा गोली पर लगाया गया बल
F = 0.01× 5000 = 50 न्यूटन।

प्रश्न 15.
एक वस्तु जिसका द्रव्यमान 1 किग्रा है, 10 मीटर / सेकण्ड के वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5 किग्रा द्रव्यमान के एक लकड़ी के गुटके से टकराती है। उसके बाद दोनों साथ-साथ उसी सीधी रेखा में गति करते हैं संघट्ट के पहले तथा बाद के कुल संवेगों की गणना कीजिए आपस में जुड़े हुए संयोजन के वेग की भी गणना कीजिए।
हल:
वस्तु का द्रव्यमान m₁ = 1 किग्रा, वेग u₁ = 10 मीटर/सेकण्ड
गुटके का द्रव्यमान m₂ = 5 किग्रा, वेग u₂ = 0 (विरामावस्था)
माना संघट्ट के बाद संयुक्त पिण्ड (m₁ + m₂), वेग v से
गति करता है,
तब संघट्ट के पहले का कुल संवेग
= m₁ u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 किग्रा मीटर / सेकण्ड
संघट्ट के बाद, संयुक्त पिण्ड का संवेग
= (m₁ + m₂) v
= (1 + 5) v
= 6 v किग्रा मीटर/सेकण्ड
संवेग संरक्षण के नियम से,
संघट्ट के बाद कुल संवेग = संघट्ट के पहले कुल संवेग
अर्थात् 6 v = 10
या v = \(\frac { 10 }{ 6 }\)
= 1.67 मीटर/सेकण्ड
अतः संघट्ट के पहले तथा बाद में कुल संवेग
= 10 किग्रा मीटर / सेकण्ड।
संघट्ट के बाद संयोजन का वेग
= 1.67 मीटर / सेकण्ड।

प्रश्न 16.
100 किग्रा द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6 सेकण्ड में 5 मीटर/सेकण्ड से 8 मीटर / सेकण्ड हो जाता है। वस्तु के पहले तथा बाद के संवेगों की गणना कीजिए। उस बल के परिमाण की गणना कीजिए जो उस वस्तु पर आरोपित है।
हल:
दिया है वस्तु का द्रव्यमान m = 100 किग्रा, प्रारम्भिक वेग u = 5 मीटर/सेकण्ड, अन्तिम वेग v = 8 मीटर / सेकण्ड समय t = 6 सेकण्ड
वस्तु का प्रारम्भिक संवेग
= mu = 100 किग्रा x 5 मीटर / सेकण्ड
= 500 किग्रा मीटर/सेकण्ड
तथा वस्तु का अन्तिम संवेग
mv = 100 किग्रा x 8 मीटर/सेकण्ड
= 800 किग्रा मीटर / सेकण्ड
∴ वस्तु के संवेग में परिवर्तन = अन्तिम संवेग – प्रारम्भिक संवेग
= 800 – 500 = 300 किग्रा मीटर/सेकण्ड
गति के द्वितीय नियम से,
वस्तु पर आरोपित बल

अतः वस्तु का प्रारम्भिक संवेग = 500 किग्रा मीटर / सेकण्ड।
वस्तु का अन्तिम संवेग = 800 किग्रा मीटर / सेकण्ड।
वस्तु पर आरोपित बल का परिमाण = 50 न्यूटन।

प्रश्न 17.
अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं, अचानक उड़ता हुआ कोई कीड़ा गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है)। अख्तर ने कहा कि चूंकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दीजिए।
उत्तर:
राहुल का तर्क सही है क्रिया-प्रतिक्रिया के नियम से दोनों पर समान बल लगेगा तथा दोनों के संवेग में भी समान परिवर्तन होगा। क्योंकि कीड़े का प्रारम्भिक संवेग, कार के संवेग की तुलना में नगण्य है अतः कीड़े का संवेग परिवर्तन स्पष्ट परिलक्षित होगा, जबकि समान संवेग परिवर्तन से कार के संवेग में कोई स्पष्ट अन्तर नहीं दिखाई देता।

प्रश्न 18.
एक 10 किग्रा द्रव्यमान की घण्टी 80 सेमी की ऊँचाई से फर्श पर गिरी। इस अवस्था में घण्टी द्वारा फर्श पर स्थानान्तरित संवेग के मान की गणना कीजिए। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान 10 मीटर / सेकण्ड² लीजिए।
हल:
दिया है घण्टी का द्रव्यमान m = 10 किग्रा, प्रारम्भिक ऊँचाई 880 सेमी 0.8 मीटर, घण्टी का त्वरण = 10 मीटर / सेकण्डर, गिरते समय प्रारम्भिक वेग u = 0
माना फर्श पर पहुँचकर घण्टी वेग से फर्श से टकराती है।
तब समीकरण v² = u² + 2as से,
v² = 0² + 2 x 10 × 0-8
= 16 मीटर/सेकण्ड²
∴ घण्टी का वेग v = \(\sqrt{16}\)
= 4 मीटर / सेकण्ड।
माना कि फर्श से टकराने के बाद घण्टी विरामावस्था में आ जाती है।
फर्श से टकराते समय घण्टी का वेग
v₁ = 4 मीटर/सेकण्ड
तथा फर्श से टकराने के बाद घण्टी का वेग v₂ = 0
घण्टी के संवेग में परिवर्तन = m (v₂ – v₁)
= 10 (0 – 4)
= 40 किग्रा – मीटर / सेकण्ड|
क्रिया-प्रतिक्रिया के नियम से फर्श को स्थानान्तरित – घण्टी का संवेग परिवर्तन
= – (- 40) = 40 किग्रा मीटर / सेकण्ड।

अतिरिक्त अभ्यास के अन्तर्गत दिए गए प्रश्न एवं उनके उत्तर (पा.पु. पृ.सं. 144)

प्रश्न 1.
एक वस्तु की गति की अवस्था में दूरी- समय सारणी निम्नवत् है-

समय (सेकण्ड)	दूरी (मीटर)
0	0
1	1
2	8
3	27
4	64
5	125
6	216
7	343

(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं? क्या यह नियत है? बढ़ रहा है? घट रहा है? या शून्य है?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं?
हल:
त्वरण तथा बल के विषय में जानकारी प्राप्त करने के लिए हम प्रत्येक समयान्तराल के लिए वेग तथा त्वरण की गणना करेंगे, जैसा कि निम्नांकित सारणी में दर्शाया गया है।
(a) निम्नलिखित सारणी से स्पष्ट है कि त्वरण नियत नहीं है, अपितु बढ़ रहा है।

(b) सूत्र बल F = m a के अनुसार, चूँकि वस्तु का त्तरण समय के साथ बढ़ रहा है; अतः वस्तु पर लगा बल भी समय के साथ बढ़ेगा।

प्रश्न 2.
1,200 किग्रा द्रव्यमान की एक कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का दिलाकर 0-2 मीटर/सेकेण्ड² का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धक्का देता है? (मान लीजिए कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
हल:
दिया है कार का द्रव्यमान m₂ = 1,200 किग्रा
प्रथम दो व्यक्तियों के धक्का देने पर त्वरण = शून्य
(∵ कार एकसमान वेग से बढ़ती है।)
तीन व्यक्तियों द्वारा धक्का देने पर त्वरण a = 0.2 मीटर/सेक्ण²
∵ प्रथम दो व्यक्तियों के धक्का देने पर कार समान वेग से ही आगे बढ़ पाती है। इससे स्पष्ट है कि दूसरी दिशा में कार में त्वरण तीसरे व्यक्ति द्वारा लगाए गए बल के कारण उत्पन्न होता है।
∴ तीसरे व्यक्ति द्वारा लगाया बल F = m a
= 1,200 किग्रा x 0.2 मीटर / सेकण्ड² = 240 न्यूटन
अतः प्रत्येक व्यक्ति द्वारा लगाया गया बल = 240 न्यूटन।

प्रश्न 3.
500 ग्राम द्रव्यमान के एक हृौड़े द्वारा 50 मीटर/सेकण्ड के वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01 सेकण्ड में ही रोका जाता है। कील के द्वारा हथौड़े पर लगाए गए बल की गणना कीजिए।
हल:
दिया है हथौड़े का द्रव्यमान m = 500 ग्राम = 0.5
किग्रा, टकराते समय वेग u = 50 मीटर / सेकण्ड,
समय t = 0.01 सेकण्ड अन्तिम वेग v = 0
कील से टकराने पर हथौड़े का त्वरण
a = \(\frac { v-u }{ t }\)
= \(\frac { 0-50 }{ 0.01 }\)
= – 5,000 मीटर / सेकण्डर²
ऋणात्मक चिह्न मन्दन की प्रदर्शित करता है। कील द्वारा हथौड़े पर लगाया गया बल F = ma
= 0.5 किग्रा x 5,000 मीटर / सेकण्ड²
= 2,500 न्यूटन।

प्रश्न 4.
एक 1,200 किग्रा द्रव्यमान की मोटरकार 90 किमी / घण्टा के वेग से एक सीधी रेखा पर चल रही है। उसका वेग बाहरी असन्तुलित बल लगने के कारण 4 सेकण्ड में घटकर 18 किमी / घण्टा रह जाता है। त्वरण और संवेग में परिवर्तन की गणना कीजिए लगने वाले बल के परिमाण की भी गणना कीजिए।
हल:
दिया है कार का द्रव्यमान m = 1,200 किग्रा,
प्रारम्भिक वेग u = 90 किमी / घण्टा
= 90 × \(\frac { 5 }{ 18 }\)
= 25 मीटर/सेकण्ड
समय t = 4 सेकण्ड, अन्तिम वेग v = 18 किमी / घण्टा
= 18 × \(\frac { 5 }{ 18 }\) = 5 मीटर / सेकण्ड
त्वरण a = ?, संवेग में परिवर्तन = ?, बल F = ?
कार का त्वरण a = \(\frac { v-u }{ t }\)
= \(\frac { 5-25 }{ 4 }\)
= – \(\frac { 20 }{ 4 }\)
= 5 मीटर/सेकण्ड
ऋणात्मक चिह्न मन्दन को प्रदर्शित करता है।
कार के संवेग में परिवर्तन अन्तिम संवेग – प्रारम्भिक संवेग
= 1200 × 5-1200 × 25
= 6000-30000
= – 24,000 किग्रा मीटर सेकण्ड
कार पर लगा बल F = ma
= 1200 × 5
= 6,000 न्यूटन
अतः कार का त्वरण = – 5 मीटर / सेकण्ड²
संवेग में परिवर्तन = 24,000 किग्रा-मीटर/सेकण्ड की कमी तथा कार पर लगा बल = 6,000 न्यूटन।

Jharkhand Board Class 9 Science बल तथा गति के नियम InText Questions and Answers

क्रियाकलाप 9.1 (पा. पु. पृ. सं. 130)
चित्रानुसार कैरम की गोटियों को एक के ऊपर एक रखकर ढेरी ननाएँ। स्ट्राइकर को तेजी से झटका देकर ढेरी की सबसे नीचे वाली गोटी पर टकराएँ। आप पायेंगे कि केवल नीचे वाली गोटी ही शीघ्रता से ढेरी से बाहर जाती है, शेष गोटियाँ अपने जड़त्व के कारण लम्वबत् दिशा में नीचे की ओर गिर जाती हैं।

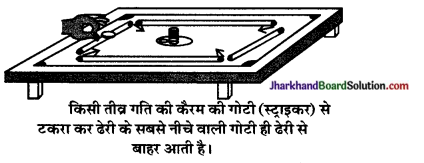
क्रियाकलाप 9.2 (पा. पु. पृ. सं. 130)
काँच के एक खाली गिलास के ऊपर एक कड़े ताश का पत्ता रखकर चित्र के अनुसार उस पर एक पाँच रुपए का सिक्का रखें तथा पत्ते को अंगुलियों से तीव्रता से क्षैतिज झटका दें। आप पायेंगे कि पत्ता आगे खिसक जाता है तथा सिक्का अपने जड़त्व के कारण नीचे की ओर गिलास में गिर जाता है। ऐसा होने का कारण यह है कि सिक्का अपनी विरामावस्था को बनाये रखना चाहता है।

क्रियाकलाप 9.3 (पा. पु. पृ. सं. 130)
ट्रे पर एक पानी से भरा गिलास रखाकर ट्रे को हाथ से पकड़कर तेजी से घूमने पर गिलास लुढ़क जाता है और पानी छलक जाता है।

खण्ड 9.3 से सम्बन्धित पाठ्य-पुस्तक के प्रश्नोत्तर (पा. पु. पृ. सं. 131)

प्रश्न 1.
निम्नलिखित में किसका जड़त्व अधिक है?
(a) रबर की गेंद एवं उसी आकार का पत्थर,
(b) एक साइकिल एवं एक रेलगाड़ी,
(c) पाँच रुपये का सिक्का एवं एक रुपये का सिक्का।
उत्तर:
हम जानते हैं कि किसी वस्तु का द्रव्यमान ही उसके जड़त्व की माप है।

• चूँकि पत्थर का द्रव्यमान, समान आकार की रबर की गेंद के द्रव्यमान से अधिक होगा; अतः पत्थर का जड़त्व ही अधिक होगा।
• रेलगाड़ी का द्रव्यमान साइकिल के द्रव्यमान से अधिक है; अत: रेलगाड़ी का जड़त्व ही अधिक होगा।
• पाँच रुपये के सिक्के का जड़त्व एक रुपये के सिक्के से अधिक होगा।

प्रश्न 2.
नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास की जिए-
“फुटबाल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।”
इसके साथ ही उस कारक की भी पहचान कीजिए, जो प्रत्येक अवस्था में बल प्रदान करता है।
उत्तर:
उपर्युक्त उदाहरण में गेंद का वेग कुल तीन बार बदलता है।

• पहली बार वेग-परिवर्तन के लिए आवश्यक बल प्रदान करने वाला कारक पहले खिलाड़ी द्वारा लगाई गई किक है।
• दूसरी बार वेग-परिवर्तन के लिए आवश्यक बल, दूसरे खिलाड़ी द्वारा लगाई गई किक से प्राप्त होता है।
• तीसरी बार वेग- परिवर्तन के लिए आवश्यक बल विपक्षी टीम के गोलकीपर द्वारा लगाई गई किक से प्राप्त होता है।

प्रश्न 3.
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं, क्यों?
उत्तर:
जब किसी पेड़ की शाखाओं को जोर-जोर से हिलाया जाता है तो शाखाएँ तुरन्त ही गति की अवस्था में आ जाती हैं, जबकि उनसे जुड़ी पत्तियाँ जड़त्व के कारण, विरामावस्था में ही बनी रहती हैं। अतः इनमें से कुछ पत्तियाँ शाखाओं से अलग होकर गिर जाती हैं।

प्रश्न 4.
जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं, और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों?
उत्तर:
ऐसा जड़त्व के कारण होता है। जब तक गाड़ी चलती रहती है तो हमारा शरीर भी गाड़ी के साथ उसी वेग से गति करता रहता है। गाड़ी के अचानक रुकने पर हमारे पैर गाड़ी के सम्पर्क में होने कारण तुरन्त विराम में आ जाते हैं, परन्तु गति जड़त्व के कारण हमारा ऊपरी शरीर आगे की ओर गति करता रहता है और हम आगे की ओर झुक जाते हैं।

जब रुकी हुई गाड़ी अचानक चलती है तो हमारे पैर तो तुरन्त गति में आ जाते हैं, परन्तु हमारा ऊपरी शरीर विराम जड़त्व के कारण विरामावस्था में बना रहता है; अतः हम पीछे की ओर झुक जाते हैं।

क्रियाकलाप 9.4. (पा. पु. पू. सं. 136)
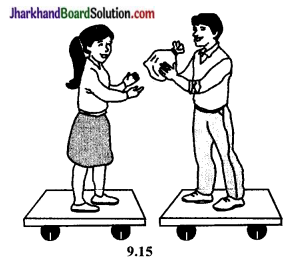
चित्र 9.15 के अनुसार दो बच्चों को पहिये वाली गाड़ी पर खड़ा होने के लिए कहें। उन्हें बालू से भरा थैला या कोई भारी वस्तु दे दें। उन्हें थैले को लपकने के लिए कहें। गाड़ी के पहिये पर कोई सफेद रेखा खीच दें, ताकि जब वे बच्चे थैले को फेंकें तो गाड़ी की गति का अवलोकन किया जा सके।

थैले को फेंकने (क्रिया) के कारण उसमें से प्रत्येक तात्क्षणिक प्रतिक्रिया का अनुभव करें। अब दो बच्चों को किसी एक गाड़ी पर खड़ा कर दें तथा एक अन्य बच्चे को दूसरी गाड़ी पर। आप यहाँ गति के द्वितीय नियम को देख सकते हैं, क्योंकि इस अवस्था में यह बल अलग-अलग त्वरण उत्पन्न करेगा।

क्रियाकलाप 9.5. (पा. पु. पृ. सं. 137)
एक बड़े आकार का गुब्बारा लेकर इसमें पूरी तरह से हवा भरकर इसके मुँह से धागा बाँधकर किसी चिपकाने वाले टेप की सहायता से चित्र $9.17$ के अनुसार एक स्ट्रॉं लगाएँ। स्ट्रॉ के बीच से एक धागे को पार कराएँ। इसके उपरान्त गुब्बारे के मुँह पर बाँधे धागे को खोल दें।

गुब्बारे में भरी हवा उसके मुख से बाहर की ओर निकलने लगेगी तथा स्ट्रो की गति की दिशा का अवलोकन करें।

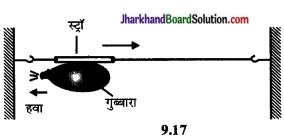
निष्कर्ष-स्ट्रॉं की दिशा हवा के निकलने की विपरीत दिशा में होगी।

क्रियाकलाप 9.6. (पा. पु. प.. सं. 138)
एक अच्छे काँच की परखनली लेकर उसमें थोड़ा पानी डालकर परखनली के मुख पर एक स्टॉप कॉर्क लगाएँ। चित्रानुसार परखनली को दो धागों के द्वारा स्टैण्ड पर क्षैतिज दिशा में लटकाएँ। अब बर्नर की सहायता

से परखनली को तब तक गर्म करें जब तक कि परखनली का पानी वाष्पित न हो जाए तथा कार्क बाहर न आ जाए।
निष्कर्ष – हम यह पाते हैं कि परखनली कार्क की गति की विपरीत दिशा में प्रक्षेपित होती है।

उदाहरण 9.6.2
kg के एक पिस्टल से 20 g द्रव्यमान की एक गोली 150ms के क्षैतिज वेग से छोड़ी जाती है। पिस्टल के पीछे हटने के वेग का परिकलन करें।
हल:
गोली का द्रव्यमान m₁ 20 ग्राम = 0.02 किग्रा
पिस्टल का द्रव्यमान m₂ = 2 किग्रा
गोली का प्रारम्भिक वेग u₁ तथा पिस्टल का प्रारम्भिक वेग u₂ क्रमशः शून्य हैं।
अर्थात्
u₁ – u₂ = 0
गोली का अन्तिम वेग v₁ = + 150 ms^-1
गोली की दिशा बाएँ से दाएँ परिपाटी के अनुसार धनात्मक (चित्र 9.19 ) ली गई है।
माना कि पिस्टल का प्रतिक्षेपित वेग v है।

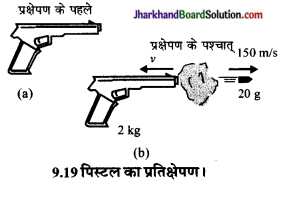
गोली छूटने के पहले गोली तथा पिस्टल का कुल संवेग,
= (2 + 0.02) kg x 0 ms^-1
= 0kg ms^-1
गोली छूटने के बाद कुल संवेग
= 0.02 kg × (+ 150 ms^-1) + 2 kg x vm s^-1
= (3 + 2v) kg ms^-1
संवेग संरक्षण के नियम के अनुसार,
गोली छूटने के बाद का कुल संवेग = गोली छूटने के पहले का कुल संवेग
3 + 2v = 0
⇒ v = – 1.5 ms^-1
ऋणात्मक चिह्न यह दर्शाता है कि पिस्टल गोली के विपरीत दिशा में अर्थात् दाई से बाई ओर प्रतिक्षेपित होगी।

उदाहरण 9.7.
40 kg द्रव्यमान वाली एक लड़की, 5 ms^-1 के क्षैतिज वेग से एक 3 kg द्रव्यमान वाली स्थिर गाड़ी पर कूदती है। गाड़ी के पहिये घर्षणरहित हैं। गाड़ी की गति प्रारम्भ करने की अवस्था में लड़की का वेग क्या होगा? मान लें कि क्षैतिज दिशा में कोई असन्तुलित बल कार्य नहीं कर रहा है।
हल:
लड़की और गाड़ी का लड़की के कूदने से पहले
कुल संवेग
= 40kg x 5ms^-1 + 3kg x 0 ms^-1
= 200 kgms^-1
मान लें कि लड़की के गाड़ी पर कूदने के बाद गाड़ी और लड़की का वेग लड़की का कुल संवेग है। इस अवस्था में गाड़ी तथा
= (40 + 3 ) kg x v ms^-1
= 43 v kg ms^-1
संवेग संरक्षण के नियमानुसार दोनों स्थितियों में कुल संवेग समान होंगे।
अर्थात्, 43 v = 200
⇒ v = 200/43 = + 4.65ms^-1
गाड़ी पर संवार लड़की 4-65 ms के वेग से छलाँग लगाने की दिशा में चलेगी (चित्र 9.20 )।

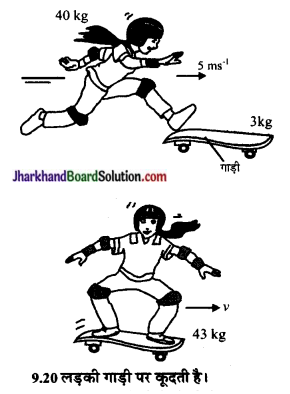
उदाहरण 9.8.
हॉकी की प्रतिद्वन्द्वी टीमों के दो खिलाड़ी गेंद को हिट करने के प्रयास में परस्पर टकरा जाते हैं तथा आपस में उलझ जाते हैं। पहले खिलाड़ी का द्रव्यमान 60 kg है तथा वह 5.0ms^-1 के वेग से गति में था, जबकि दूसरा खिलाड़ी जिसका द्रव्यमान 55 kg है तथा वह 6.0ms^-1 के वेग से पहले खिलाड़ी की ओर गति कर रहा था। टकराकर उलझने के बाद वे दोनों किस दिशा में किस वेग से गति करेंगे। मान लें कि दोनों खिलाड़ियों के पैर तथा पृथ्वी के बीच कार्यरत घर्षण बल नगण्य है।
हल:
मान लें कि पहला खिलाड़ी बाएँ से दाएँ दौड़ रहा है। परिपाटी के अनुसार, बाएँ से दाएँ गति की दिशा धनात्मक और दाएँ से बाएँ गति की दिशा को ऋणात्मक लेते हैं (चित्र 9. 21)। प्रतीक तथा दोनों खिलाड़ियों के क्रमश: द्रव्यमान और वेग को दर्शाते हैं। इन भौतिक राशियों पर अधोलिखित संख्याएँ तथा 2 क्रमश: प्रथम एवं द्वितीय हॉकी खिलाड़ियों को बताती हैं। अतः

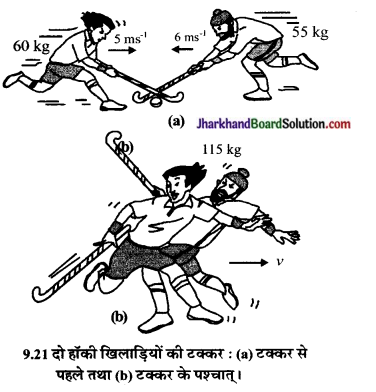
m₁ = 60kg; u₁
= + 5ms^-1 तथा
m₂ = 55 kg: u₂
= – 6ms^-1
टक्कर से पहले दोनों खिलाड़ियों का कुल संवेग
= 60 kg × (+ 5ms^-1) + 55 kg x (- 6ms^-1)
= – 30kgms^-1
मान लें कि दोनों खिलाड़ियों के टकराने के बाद उलझने पर वेग v है, टक्कर के बाद कुल संवेग
= (m₁ + m₂) x v
=(60 + 55) kg x v ms^-1
= 115 x v kg ms^-1
संवेग संरक्षण के नियमानुसार टक्कर से पहले तथा बाद के संवेगों की समानता से,
v = – 30/115 = – 0.26ms^-1
अतः उलझने के बाद दोनों खिलाड़ी दाएँ से बाएँ 0.26 ms^-1 के वेग से गतिशील होंगे।

खण्ड 9.6 से सम्बन्धित पाठ्य पुस्तक के प्रश्न (पा.पु. पृ. सं. 140)

प्रश्न 1.
यदि क्रिया सदैव प्रतिक्रिया के बराबर होती है तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता है?
उत्तर:
घोड़ा गाड़ी की गति- घोड़ा गाड़ी को खींचते समय अपने पैरों से सड़क पर पीछे की ओर बल लगाता है। क्रिया-प्रतिक्रिया के नियम के अनुसार सड़क भी घोड़े पर समान परिमाण का बल आगे की ओर लगाती है। इसी प्रतिक्रिया बल के कारण घोड़ा तथा उसके पीछे जुड़ी गाड़ी आगे की ओर चल पड़ते हैं। इस प्रकार घोड़ा व गाड़ी घोड़े द्वारा लगाए बल के कारण नहीं बल्कि पृथ्वी के प्रतिक्रिया बल के कारण गतिमान होते हैं।

प्रश्न 2.
एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबर की नली को पकड़ने में कठिनाई क्यों होती है? स्पष्ट कीजिए।
उत्तर:
फायर ब्रिगेड की अत्यधिक मात्रा उच्च वेग से मोटर के पाइप से पानी की निकलती है अर्थात् पाइप से निकलने वाले पानी की संवेग परिवर्तन की दर बहुत अधिक होती है। क्रिया-प्रतिक्रिया के नियम से, पाइप का संवेग भी इसी दर से विपरीत दिशा में परिवर्तित होता है। इसका अर्थ यह हुआ कि पाइप से निकलने वाला पानी पाइप पर बहुत अधिक बल आरोपित करता है जिसके कारण पाइप को सँभालना कठिन होता है।

प्रश्न 3.
एक 50 ग्राम द्रव्यमान की गोली 4 किग्रा द्रव्यमान की रायफल से 35 मीटर / सेकण्ड के प्रारम्भिक वेग से छोड़ी जाती है। रायफल के प्रारम्भिक प्रतिक्षेपित वेग की गणना कीजिए।
हल:
दिया है गोली का द्रव्यमान m₁ = 50 ग्राम = \(\frac { 50 }{ 1000 }\) किग्रा = 0.05 किग्रा।
गोली के छूटने का वेग v₁ = 35 मीटर / सेकण्ड
रायफल का द्रव्यमान m₂ = 4 किग्रा,
रायफल का प्रतिक्षेपित वेग v₂ = ?
∵ गोली में विस्फोट होने से पूर्व गोली तथा रायफल दोनों विरामावस्था में थीं,
∴ विस्फोट से पूर्व दोनों का कुल संवेग
= m₁u₁ + m₂ u₂
= m₁ x 0 + m₂ x 0 = 0 [∴ u₁ = 0, u₂ = 0]
तथा विस्फोट के बाद दोनों का संवेग
= m v₁ + m₂ v₂
= 0.05 x 35 + 4v₂
संवेग संरक्षण के नियम से, दोनों संवेगों को बराबर
रखने पर,
0.05 x 35 + 4v₂ = 0
या 4v₂ = 0.05 x 35 = – 1.75
या v₂ = – \(\frac { 1.75 }{ 4 }\)
= – 0.4375 मीटर/सेकण्ड।
ऋणात्मक चिह्न यह प्रदर्शित करता है कि रायफल गोली के विपरीत दिशा में गति करेगी।
अतः रायफल का प्रतिक्षेपित वेग = 0-4375 मीटर / सेकण्ड पीछे की ओर।

प्रश्न 4.
100 ग्राम तथा 200 ग्राम द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमश: 2 मीटर / सेकण्ड तथा 1 मीटर/सेकण्ड के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1-67 मीटर/सेकण्ड हो जाता है तो दूसरी वस्तु का वेग ज्ञात कीजिए।
हल:
दिया है द्रव्यमान m₁ = 100 ग्राम 0.1 किग्रा, m₂ = 200 ग्राम 0-2 किग्रा
टक्कर से पूर्व वेग u₁ = 2 मीटर/सेकण्ड,
u₂ = 1 मीटर/सेकण्ड
टक्कर के बाद वेग v₁ = 1.67 मीटर / सेकण्ड, v₂ = ?
टक्कर से पूर्व दोनों का संवेग = m₁ u₁ + m₂ u₂
= 0.1 × 2 + 0.2 × 1
= 0.4 किग्रा मीटर/सेकण्ड
तथा टक्कर के बाद दोनों का संवेग = m₁ v₁ + m₂ v₂
= (0.1 × 1.67 + 0.2 × 12 ) किग्रा – मीटर / सेकण्ड संवेग संरक्षण के नियम से,
टक्कर के बाद संवेग = टक्कर से पूर्व संवेग
अर्थात् 0.1 × 1.67 + 0.2 x v₂ = 0.4
या 0.2 x v₂ = 0-4 – 0.167
0.2 × v₂ = 0.233
या v₂ = \(\frac { 0.233 }{ 0.2 }\)
= 1.165 मीटर / सेकण्ड
अतः टक्कर के बाद दूसरी वस्तु का वेग 1.165 मीटर / सेकण्ड होगा।