Jharkhand Board JAC Class 10 Science Important Questions Chapter 14 उर्जा के स्रोत Important Questions and Answers.
JAC Board Class 10 Science Important Questions Chapter 14 उर्जा के स्रोत
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
ऊर्जा का मूल स्रोत क्या है?
उत्तर:
ऊर्जा का मूल स्रोत सूर्य है, जिसके अंतरंग में नाभिकीय संलयन क्रिया हो रही है।
प्रश्न 2.
सूर्य में ऊर्जा उत्पत्ति का कारण क्या है?
उत्तर:
सूर्य के अंतरंग में उपस्थित हाइड्रोजन परमाणुओं के नाभिकीय संलयन की क्रिया ही ऊर्जा उत्पत्ति का कारण है।
प्रश्न 3.
दृश्य प्रकाश की तरंग दैर्ध्य सीमा क्या है?
उत्तर:
दृश्य प्रकाश की तरंग दैर्ध्य सीमा है- 4000 से 70004 तक अथवा तरंग दैर्ध्य 4 x 10-7 मी से 7 x 10-7 मी
प्रश्न 4.
प्रकाश संश्लेषण के लिए प्रकाश का कौन-सा घटक उत्तरदायी है?
उत्तर:
प्रकाश संश्लेषण के लिए प्रकाश का घटक दृश्य प्रकाश उत्तरदायी है।
प्रश्न 5.
पवन ऊर्जा के उपयोग के लिए बनाई दो युक्तियों के नाम बताइये।
उत्तर:
पवन चक्की, जलपम्प।
प्रश्न 6.
सागरीय तापीय ऊर्जा किसे कहते हैं?
उत्तर:
महासागर की सतह के जल तथा गहराई के जल के ताप में अन्तर के कारण उपलब्ध ऊर्जा को सागरीय तापीय ऊर्जा कहते हैं।
प्रश्न 7.
सूर्य के नाभिक में हाइड्रोजन का कौन-सा समस्थानिक होता है?
उत्तर:
सूर्य के नाभिक में हाइड्रोजन का भारी समस्थानिक ड्यूटेरियम \(\left({ }_1 \mathrm{H}^2\right)\) होता है।
प्रश्न 8.
दो नाभिकीय ईंधनों के नाम लिखिए।
उत्तर:
दो नाभिकीय ईंधनों के नाम हैं-
- U-235 ( यूरेनियम 235)
- Pu – 239 (प्लूटोनियम-239)

प्रश्न 9.
श्रृंखला अभिक्रिया के प्रकारों के नाम लिखो।
उत्तर:
शृंखला अभिक्रिया दो प्रकार की होती है-
- नियन्त्रित (या सीमित) श्रृंखला अभिक्रिया।
- अनियन्त्रित (या असीमित) शृंखला अभिक्रिया।
प्रश्न 10.
नाभिकीय संलयन को परिभाषित कीजिए।
उत्तर:
अति उच्च दाब तथा उच्च ताप (लगभग 107K) पर दो हल्के नाभिकों का परस्पर संयुक्त होकर एक भारी नाभिक बनाने की अभिक्रिया को नाभिकीय संलयन कहते हैं। इस अभिक्रिया में असीमित ऊर्जा मुक्त होती है।
प्रश्न 11.
नाभिकीय ऊर्जा क्या है?
उत्तर:
पदार्थ के परमाणुओं के केन्द्र में स्थित नाभिक असीमित ऊर्जा के भण्डार हैं। इसी ऊर्जा को नाभिकीय ऊर्जा कहते हैं। प्रायः ये नाभिकीय संलयन एवं नाभिकीय विखण्डन के फलस्वरूप मुक्त होती है।
प्रश्न 12.
यूरेनियम के दो समस्थानिकों के नाम व संकेत लिखिए।
उत्तर:
यूरेनियम के दो समस्थानिक हैं-
- यूरेनियम-235 या \({ }_{92} \mathrm{U}^{235}\)
- यूरेनियम-238 या \({ }_{92} \mathrm{U}^{238}\)
प्रश्न 13.
सूर्य में ऊर्जा का मुख्य स्रोत क्या है?
उत्तर:
सूर्य में ऊर्जा का मुख्य स्रोत हाइड्रोजन की संलयन क्रिया है।
प्रश्न 14.
नाभिकीय रियेक्टर में प्रयुक्त ईंधन का नाम लिखिए।
उत्तर:
नाभिकीय रियेक्टर में प्रयुक्त ईंधन है- यूरेनियम – 235 या \({ }_{92} \mathrm{U}^{235}\)।
प्रश्न 15.
\({ }_{92} \mathrm{U}^{235}\) के नाभिक में प्रोटॉनों तथा न्यूट्रॉनों की संख्या लिखिए।
उत्तर:
\({ }_{92} \mathrm{U}^{235}\) के नाभिक में-
प्रोटॉनों की संख्या = 92
न्यूट्रॉनों की संख्या = 235 – 92 = 143
प्रश्न 16.
परमाणु बम एवं हाइड्रोजन बम में होने वाली क्रियाओं के नाम लिखिए।
उत्तर:
परमाणु बम नाभिकीय विखण्डन एवं हाइड्रोजन बम में नाभिकीय संलयन की क्रियाएँ होती हैं। दोनों में ही अनियन्त्रित श्रृंखला अभिक्रिया होती है।
प्रश्न 17.
नाभिकीय संलयन में ऊर्जा का स्रोत क्या है?
उत्तर:
नाभिकीय संलयन में ऊर्जा का स्रोत हाइड्रोजन के समस्थानिक ड्यूटेरियम हैं।
प्रश्न 18.
नाभिकीय रियेक्टर में प्रयुक्त मन्दक का नाम लिखिए।
उत्तर:
नाभिकीय रियेक्टर में प्रयुक्त मन्दक भारी जल (D2O) अथवा ग्रेफाइट हैं।
प्रश्न 19.
\({ }_{92} \mathrm{U}^{238}\) से क्या तात्पर्य है?
उत्तर:
\({ }_{92} \mathrm{U}^{238}\) यूरेनियम का वह स्थायी समस्थानिक है जिसके नाभिक में 92 प्रोटॉन तथा 146 न्यूट्रॉन होते हैं।

प्रश्न 20.
नाभिकीय विखण्डन क्या है?
उत्तर:
नाभिकीय विखण्डन- एक भारी नाभिक पर मन्द न्यूट्रॉन की बमबारी करने पर उसके लगभग समान आकार के दो हल्के नाभिकों में टूटने की क्रिया को नाभिकीय विखण्डन कहते हैं। इस क्रिया में अपार ऊर्जा उत्सर्जित होती है।
प्रश्न 21.
नाभिकीय विखण्डन का महत्त्वपूर्ण उपयोग क्या है?
उत्तर:
नाभिकीय विखण्डन का महत्त्वपूर्ण उपयोग मानव कल्याण हेतु रचनात्मक कार्यों जैसे विद्युत उत्पादन करने में होता है।
प्रश्न 22.
समस्थानिक किसे कहते हैं?
उत्तर:
किसी तत्त्व विशेष के दो या दो से अधिक ऐसे परमाणु जिनका परमाणु क्रमांक समान हो किन्तु परमाणु द्रव्यमान भिन्न-भिन्न समस्थानिक कहलाते हैं, जैसे यूरेनियम के दो समस्थानिक \({ }_{92} \mathrm{U}^{235}\) एवं \({ }_{92} \mathrm{U}^{238}\) होते हैं।
प्रश्न 23.
ऊर्जा किस रूप में स्थानान्तरित होती है?
उत्तर:
ऊर्जा तरंगों के रूप में स्थानान्तरित होती है। इन ऊर्जा तरंगों का तरंग दैर्ध्य भिन्न-भिन्न होता है। ऊर्जा की सभी तरंगों का उद्गम सूर्य से होता है।
प्रश्न 24.
ऊर्जा का विशाल स्त्रोत क्या है?
उत्तर:
सूर्य ऊर्जा के सभी रूपों का विशाल स्रोत है।
प्रश्न 25.
दृश्य प्रकाश में सबसे कम तरंगदैर्ध्य किस रंग की है?
उत्तर:
दृश्य प्रकाश में सबसे कम तरंगदैर्घ्य बैंगनी रंग की है।
प्रश्न 26.
दृश्य प्रकाश में सबसे अधिक तरंगदैर्ध्य किस रंग की है?
उत्तर:
दृश्य प्रकाश में सबसे अधिक तरंग दैर्ध्य लाल रंग की है।
प्रश्न 27.
प्रकाश की कौन-सी तरंगों में गर्म करने का गुण पाया जाता है?
उत्तर:
प्रकाश की अवरक्त तरंगों में गर्म करने का गुण पाया जाता है।
प्रश्न 28.
सौर ऊर्जा को किन-किन रूपों में रूपान्तरित किया जा सकता है?
उत्तर:
सौर ऊर्जा को ऊष्मा ऊर्जा, प्रकाश ऊर्जा, विद्युत ऊर्जा आदि रूपान्तरित किया जा सकता है।
प्रश्न 29.
उन तत्त्वों के नाम लिखिए, जिनका उपयोग सौर सेल के निर्माण में किया जाता है।
उत्तर:
सौर सेल सिलिकॉन तथा गैलेनियम जैसे अर्द्ध-चालकों से बनाए जाते हैं।
प्रश्न 30.
हमारी पृथ्वी से सूर्य कितनी दूरी पर है?
उत्तर:
हमारी पृथ्वी से सूर्य 15 करोड़ किलोमीटर दूर स्थित है।
प्रश्न 31.
सूर्य का द्रव्यमान क्या है?
उत्तर:
सूर्य का द्रव्यमान लगभग 1029 टन है।
प्रश्न 32.
सूर्य कितने वर्षों से जल रहा है?
उत्तर:
जीवाश्मों के आधार पर यह अनुमान लगाया जाता है कि सूर्य पिछले सात से आठ अरब वर्षों से प्रदीप्तमान है।

प्रश्न 33.
सूर्य का सम्पूर्ण प्रायः द्रव्यमान किस तत्त्व के कारण है?
उत्तर:
सूर्य का सम्पूर्ण प्रायः द्रव्यमान हाइड्रोजन तत्त्व के कारण है।
प्रश्न 34.
सूर्य से विकरित दो अदृश्य प्रकाश किरणों के नाम लिखिए।
उत्तर:
सूर्य से विकरित दो अदृश्य प्रकाश किरणें पराबैंगनी तथा अवरक्त प्रकाश किरणें हैं।
प्रश्न 35.
पृथ्वी के वायुमण्डल के ऊपरी सतह के प्रति वर्गमीटर क्षेत्रफल में सूर्य की कितनी ऊर्जा प्राप्त होती है?
उत्तर:
पृथ्वी के वायुमण्डल की ऊपरी सतह सूर्य से लगभग 1.36 जूल ऊर्जा प्रति सेकण्ड प्रति वर्ग मीटर प्राप्त करती है। इसका कुछ भाग अंतरिक्ष में परावर्तित हो जाता है तथा कुछ भाग वायुमण्डल में उपस्थित जल वाष्प, ओजोन, धूल तथा CO2 द्वारा अवशोषित कर लिया जाता है।
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
सूर्य में ऊर्जा उत्पत्ति की क्रिया को समझाइये।
उत्तर:
सूर्य के क्रोड में हाइड्रोजन व हीलियम विशाल मात्रा में हैं। ये तत्त्व परमाण्विक अवस्था में है। हाइड्रोजन परमाणु सूर्य के क्रोड में अति तीव्र वेग से सभी दिशाओं गमन कर रहे हैं हैं तथा एक-दूसरे टकरा रहे हैं। प्रयोगों से यह स्थापित किया गया है कि जब हाइड्रोजन परमाणु संलयन द्वारा (जुड़कर) हीलियम के अधिक भारी परमाणु बनाते हैं, तो अति विशाल मात्रा में ऊर्जा उत्सर्जित होती है।
परमाणुओं के नाभिकों के जुड़ने की इस क्रिया संलयन कहते हैं। सूर्य के क्रोड में यह प्रक्रिया निरन्तर व अबाध गति से हो रही है। यह क्रिया कई चरणों में को होती है। प्रथमतः हाइड्रोजन के दो नाभिक संलयित होकर भारी हाइड्रोजन, जिसे ड्यूटीरियम कहते हैं का एक परमाणु निर्मित करते हैं, तत्पश्चात् ड्यूटीरियम के दो परमाणु संलयन द्वारा हीलियम के एक नाभिक की रचना करते हैं।
प्रश्न 2.
सौर ऊर्जा के दो लाभ बतायें।
उत्तर:
सौर ऊर्जा के दो लाभ निम्न हैं-
- सौर ऊर्जा से विद्युत ऊर्जा प्राप्त की जाती है जो बिल्कुल प्रदूषण रहित होती है।
- सौर ऊर्जा के उपयोग से कोयले तथा पेट्रोलियम जैसे अनवीकरणीय ऊर्जा स्रोत को संरक्षित किया जा सकता है।
प्रश्न 3.
सौर सेल और सौर पैनल में क्या अन्तर है?
उत्तर:
सौर सेल और सौर पैनल में निम्नलिखित अन्तर हैं-
| सौर सेल | सौर पैनल |
| 1. सौर सेल अर्द्ध चालक युक्त वह युक्ति है जो सौर ऊर्जा की अत्यल्प मात्रा को विद्युत ऊर्जा में परिवर्तित कर देती है। | 1. सौर पैनल, बहुत बड़ी संख्या में सौर सेल को एक विशेष क्रम में जोड़कर बनायी गई युक्ति है। |
| 2. इसकी दक्षता बहुत कम होती है। | 2. इसकी दक्षता आवश्यकतानुसार बढ़ायी जा सकती है। |
| 3. सौर सेल अधिक ऊर्जा वाले उपकरणों को चालित नहीं कर पाता है। | 3. सौर पैनल द्वारा उत्पादित ऊर्जा को संचायक बैटरी में भण्डारित किया जा सकता है, इसलिए इससे अधिक ऊर्जा वाले उपकरणों को भी चालित किया जा सकता है। |
प्रश्न 4.
बड़े बाँध किस प्रकार विद्युत उत्पादन में सहायक क्षं?
उत्तर:
सौर ऊर्जा द्वारा प्रकृति में जल चक्र के रूप में जल का पुन: चक्रण होता रहता है। वर्षा का पानी नदियों में बहता रहता है जो हमें जल ऊर्जा उपलब्ध करवाता है। नदियों के इस पानी को बाँध बनाकर संगृहित कर दिया जाये तो नदियों के पानी की गतिज ऊर्जा बाँधों में स्थितिज ऊर्जा के रूप में संचित हो जाती है।
बाँध में एकत्र पानी का बाँध के नीचे जल विद्युत संयंत्र लगाकर उसके टरबाइन पर गिराये जाने पर बाँध के स्थिर पानी की स्थितिज ऊर्जा गतिज ऊर्जा में बदल जाती है जिससे टरबाइन घूमने लगते हैं फलस्वरूप जल विद्युत संयंत्र का आर्मेचर घूमने लगता है तथा विद्युत उत्पन्न हो जाती है। इस प्रकार प्रकृति से प्राप्त जल ऊर्जा का विद्युत ऊर्जा उत्पादन में बड़े बाँध सहायक है।
प्रश्न 5.
बॉक्सनुमा सौर कुकर का नामांकित चित्र बनाइए।
उत्तर:
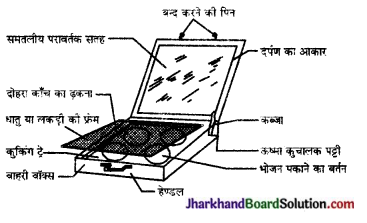
प्रश्न 6.
बॉक्सनुमा सौर कुकर तथा गोलीय परावर्तक युक्त सौर कुकर में चार अन्तर लिखिए।
उत्तर:
बॉक्सनुमा सौर कुकर तथा गोलीय परावर्तक सौर कुकर में अन्तर निम्नलिखित हैं-
| बॉक्सनुमा सौर कुकर | गोलीय परावर्तक युक्त सौर कुकर |
| 1. इससे रात में भोजन नहीं पकाया जा सकता है। | 1. इसमें अवतल अथवा परवलयिक परावर्तक होता है जो सौर ऊर्जा को एक छोटे-से क्षेत्र में संकेन्द्रित कर देता है। |
| 2. यह उस स्थान के लिए उपयोगी नहीं है जहाँ हमेशा बादल छये रहते हैं। | 2. इसमें अपेक्षाकृत काफी उच्च ताप प्राप्त होता है। |
| 3. इसे हम किसी भी स्थान पर नहीं रख सकते हैं। | 3. यह तीव्र आँच में पकने वाले खाद्य पदार्थों के लिए उपयोगी है। |
| 4. इसका उपयोग सेंकने या तलने के लिए नहीं किया जा सकता है। | 4. यह सेंकने तथा तलने के लिए भी उपयोग किया जा सकता है। |
प्रश्न 7.
सौर ऊर्जा का स्रोत क्या है?
उत्तर:
सौर ऊर्जा का स्रोत इसके केन्द्र में हो रहे हाइड्रोजन परमाणु की नाभिकीय संलयन क्रिया है। इस अभिक्रिया में दो हल्के हाइड्रोजन परमाणु के नाभिक परस्पर संयुक्त होकर एक भारी एवं स्थायी हीलियम का नाभिक बनाते हैं तथा अत्यधिक परिमाण में ऊर्जा विमोचित करते हैं। यही ऊर्जा सौर ऊर्जा है। इसे निम्न समीकरण द्वारा दर्शाया जाता है-
\({ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H} \longrightarrow{ }_2^4 \mathrm{He}\) + ऊर्जा
प्रश्न 8.
पराबैंगनी किरणें क्या हैं? इसके गुण लिखिए।
उत्तर:
पराबैंगनी किरणें-ये वे चुम्बकीय तरंगें हैं जिनकी तरंग दैर्ध्य 1 x 10-8 मी से 4 x 10-7 मी तक होती है। ये अदृश्य किरणें हैं जिनकी पहचान फोटोग्राफिक फिल्म द्वारा की जाती है।
पराबैंगनी किरणों के गुण-
- ये अदृश्य किरणें हैं।
- ये फोटोग्राफिक प्लेट को काला कर देती हैं।
- इसकी अधिक मात्रा मानव जीवन के लिए हानिकारक होती है।
प्रश्न 9.
सूर्य प्रकाश के प्रमुख संघटकों को संक्षेप में समझाइये।
उत्तर:
सूर्य प्रकाश के तीन प्रमुख संघटक हैं-
- पराबैंगनी प्रकाश- बैंगनी रंग की तरंग दैर्ध्य से कम तरंग दैर्ध्य वाले प्रकाश को पराबैंगनी प्रकाश कहते हैं। यह मानव नेत्र द्वारा दिखाई नहीं देता तथा सभी सजीवियों के लिए हानिकारक होता है।
- दृश्य प्रकाश बैंगनी रंग से लाल रंग तक के तरंग दैर्ध्य वाले प्रकाश को दृश्य प्रकाश कहते हैं। यह मानव नेत्र द्वारा दिखाई देता है।
- अवरक्त प्रकाश- लाल रंग की तरंग दैर्ध्य से अधिक तरंग दैर्ध्य वाले प्रकाश को अवरक्त प्रकाश कहते हैं। यह भी मानव नेत्र द्वारा दिखाई नहीं देता है।

प्रश्न 10.
सोलर सेल क्या है? इसके कोई तीन उपयोग लिखिए।
उत्तर:
सोलर सेल- सोलर सेल वह है जो सौर प्रकाश को सीधे ही विद्युत में रूपान्तरित कर देती है।
सोलर सेल के उपयोग-
- विद्युत स्रोत के रूप में समस्त कृत्रिम उपग्रहों में किया जाता है।
- केलकुलेटर, घड़ियाँ तथा अन्य छोटे उपकरणों को चलाने में।
- प्रकाश व्यवस्था में रेडियो तथा दूरदर्शन के अभिग्राहियों को प्रचलित करने में।
प्रश्न 11.
सोलर कुकर के चार लाभ लिखिए।
उत्तर:
सोलर कुकर के लाभ-
- सोलर कुकर के उपयोग से ईंधन की बचत होती है।
- सोलर कुकर में धुआँ नहीं निकलता जिससे पर्यावरण प्रदूषित नहीं होता।
- इसके उपयोग से भोजन के पोषक तत्त्व नष्ट नहीं होते।
- इसे इच्छित स्थान पर ले जाया जा सकता है।
प्रश्न 12.
सोलर कुकर की कोई चार सीमाएँ लिखिए।
उत्तर:
सोलर कुकर की सीमाएँ-
- इससे रात में भोजन नहीं पकाया जा सकता है।
- यह उस स्थान के लिए उपयोगी नहीं है जहाँ हमेशा बादल छाये रहते हैं।
- इसे हम किसी भी स्थान पर नहीं रख सकते हैं।
- इसका उपयोग सेंकने या तलने के लिए नहीं किया जा सकता है।
प्रश्न 13.
सौर ऊष्मक (हीटर) किस सिद्धान्त पर कार्य करता है?
उत्तर:
सौर ऊष्मक काले रंग प्रयोग किया जाता है जो ऊष्मा का अच्छा अवशोषक किन्तु बुरा परावर्तक होने के कारण प्रकाश ऊर्जा का ऊष्मीय विकिरण (अवरक्त प्रकाश) को अवशोषित कर लेता है, फलत: सौर ऊष्मक में रखी वस्तु गर्म हो जाती है। अधिक ऊष्मा प्राप्त करने के लिए दर्पणों का प्रयोग किया जाता है जो प्रकाश को एकत्र करने का कार्य करते हैं।
प्रश्न 14.
सूर्य का हमारे लिए क्या महत्त्व है?
उत्तर:
सूर्य निम्नलिखित कारणों से हमारे लिए महत्त्वपूर्ण है-
- सूर्य हमारे लिए ऊर्जा का सबसे अधिक प्रत्यक्ष एवं विशाल स्रोत है।
- यह पृथ्वी पर वायु प्रवाह तथा जल चक्र की निरन्तरता बनाये रखने के लिए आवश्यक शक्ति प्रदान करता है।
- यह पृथ्वी के समस्त जीवन को संपोषित करता है।
- सूर्य द्वारा विकरित ऊर्जा को यान्त्रिक ऊर्जा में परिवर्तित करके हम अपने विभिन्न कार्यों को सम्पन्न करते हैं।
प्रश्न 15.
जल ऊर्जा किसे कहते हैं? इसके दो उपयोग लिखिए।
उत्तर:
जल ऊर्जा – बहते हुए जल में बहुत ज्यादा मात्रा में गतिज ऊर्जा होती है जिससे यान्त्रिक कार्य किये जा सकते हैं, इसे ही जल ऊर्जा कहते हैं।
उपयोग-
- जल चक्कियों के पार्टी को घुमाने में।
- जलविद्युत संयंत्र को संचालित कर विद्युत उत्पन्न करने में।
प्रश्न 16.
जल विद्युत का क्या अर्थ है?
उत्तर:
बहते हुए जल की ऊर्जा का उपयोग करके जो विद्युत उत्पन्न की जाती है, उसे जल विद्युत कहते हैं। जल की स्थितिज ऊर्जा को गतिज ऊर्जा में बदलकर टरबाइन की सहायता से जनरेटर को चलाया जाता है, इससे जनरेटर की कुण्डलियों में विद्युत धारा प्रवाहित होने लगती है। इस विद्युत को ही जल विद्युत कहते हैं।
प्रश्न 17.
आँधियाँ कैसे उत्पन्न होती हैं?
उत्तर:
वायु की दो सन्निकट पट्टिकाओं में असमान ऊष्माग्राहिता के कारण तापान्तर उत्पन्न होता है तब ठण्डी वावु पट्टिका अति तीव्र गति से दाब डालती हुई ऊष्ण वायु पट्टिका की ओर बढ़ती है। चूँकि उष्ण पट्टिका उसी गति से उस स्थान से प्रस्थान नहीं कर पाती, अतः दोनों वायु पट्टिकाओं में टकराहट (संघट्ट) होती है। इसके फलस्वरूप औधियाँ उत्पन्न होती हैं।
प्रश्न 18.
वायु का प्रवाह कैसे उत्पन्न होता है?
उत्तर:
भूमध्यरेखीय स्थानों पर सूर्य की किरणें सीधी पड़ती हैं अतः वे स्थान अधिक गर्म हो जाते हैं। दूसरी ओर ध्रुवों पर सूर्य की किरणें तिरछी पड़ती हैं अतः वे अपेक्षाकृत कम गर्म हो पाते हैं। इस तापान्तरण के कारण वायुमण्डल में अलग-अलग तापों की परतें बन जाती हैं। गर्म वायु हल्की होने के कारण ऊपर उठ जाती है और भूमध्य रेखीय वायुमण्डल में गरम वायु जमा हो जाती उधर ध्रुव प्रदेशों में ठण्डी वायु पृथ्वी के तल के और पास आ जाती है। इस प्रकार वायुमण्डल में वायु का प्रवाह पृथ्वी तल के समीप ध्रुवों से भूमध्य रेखा की ओर होने लगता है, यही वायु प्रवाह या पवन है।
प्रश्न 19.
ऊर्जा संकट के कोई दो कारण लिखो।
उत्तर:
ऊर्जा संकट के कारण निम्नलिखित हैं-
- जनसंख्या में अत्यधिक वृद्धि के कारण अनवीकरणीय ऊर्जा स्रोतों का अत्यन्त दोहन करना।
- कम दक्षता वाली मशीनों के उपयोग के कारण ऊर्जा के अधिकांश भाग का ह्रास हो जाना।
प्रश्न 20.
नाभिकीय रियेक्टर क्या है?
उत्तर:
नाभिकीय रियेक्टर वह युक्ति है जिसमें नाभिकीय विखण्डन की श्रृंखला अभिक्रिया को नियन्त्रित करके अत्यधिक ऊर्जा प्राप्त की जाती है जिसका उपयोग विभिन्न रचनात्मक कार्यों हेतु किया जाता है। वास्तव में नाभिकीय रियेक्टर नाभिकीय विखण्डन की क्रिया द्वारा उत्पन्न ऊष्मीय ऊर्जा से टरबाइन चलाकर विद्युत ऊर्जा उत्पन्न करता है।
प्रश्न 21.
श्रृंखला अभिक्रिया से क्या समझते हैं?
उत्तर:
शृंखला अभिक्रिया ऐसी नाभिकीय विखण्डन अभिक्रिया जिसमें अभिक्रिया को प्रारम्भ करने वाला न्यूट्रॉन, अभिक्रिया के दौरान भी उत्पन्न होता है तथा अभिक्रिया को लगातार आगे बढ़ाता रहता है, शृंखला अभिक्रिया कहलाती है।
जब मन्दगामी न्यूट्रॉन की यूरेनियम-\(\left({ }_{92} \mathrm{U}^{235}\right)\) पर बमबारी की जाती है तो प्रत्येक यूरेनियम नाभिक लगभग समान आकार के दो खण्डों में टूट जाता है तथा तीन नये न्यूट्रॉन, X-किरणें तथा ऊपर अपार मात्रा में ऊर्जा उत्सर्जित होती है। ये नये न्यूट्रॉन अनुकूल ‘परिस्थितियों में अन्य यूरेनियम नाभिकों का विखण्डन करते हैं। इस प्रकार नाभिकों के विखण्डन की एक श्रृंखला बन जाती है जो एक बार प्रारम्भ होने पर स्वतः ही जारी रहता है जब तक समस्त यूरेनियम समाप्त नहीं हो जाता है, यह सम्पूर्ण अभिक्रिया शृंखला अभिक्रिया कहलाती है।
प्रश्न 22.
नाभिकीय संलयन क्या है? एक उदाहरण देकर समझाइए।
अथवा
नाभिकीय संलयन को चित्र द्वारा समझाइये।
उत्तर:
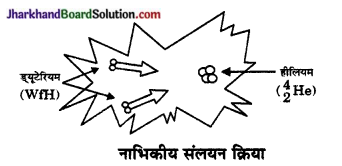
नाभिकीय संलयन- अति उच्च दाब एवं उच्च ताप ( लगभग 107K) पर दो हल्के नाभिकों का परस्पर संयुक्त होकर एक भारी नाभिक बनाने की अभिक्रिया को नाभिकीय संलयन कहते हैं। इस अभिक्रिया में असीमित ऊर्जा मुक्त होती है।
उदाहरण- हाइड्रोजन के समस्थानिक ड्यूटेरियम के दो नाभिक \(\left({ }_1^2 \mathrm{H}\right)\) संलयित होकर एक हीलियम नाभिक \(\left({ }_4^2 \mathrm{He}\right)\) बनाते हैं तो बहुत अधिक ऊर्जा मुक्त होती है।
\({ }_1^2 \mathrm{H}+{ }_1^2 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}+21.6\)MeV ऊर्जा
प्रश्न 23.
नाभिकीय ऊर्जा के कोई तीन लाभ लिखिए।
उत्तर:
नाभिकीय ऊर्जा के लाभ-
- U-235, की छोटी-सी मात्रा से अत्यधिक मात्रा में ऊर्जा मुक्त होती है।
- नाभिकीय विखण्डन के लिए ऑक्सीजन की आवश्यकता नहीं होती है।
- यूरेनियम पर्याप्त मात्रा में उपलब्ध होने पर नाभिकीय ऊर्जा हमेशा मिल सकती है।
प्रश्न 24.
नाभिकीय विखण्डन के महत्त्वपूर्ण उपयोग क्या हैं?
उत्तर:
नाभिकीय विखण्डन का उपयोग निम्नलिखित कार्यों होता है-
- नाभिकीय विखण्डन की श्रृंखला अभिक्रिया को नियन्त्रित करके इससे प्राप्त ऊर्जा को विद्युत उत्पादन हेतु उपयोग में लाया जाता है।
- नाभिकीय विखण्डन से प्राप्त उत्पादों का उपयोग उद्योग, कृषि तथा चिकित्सा के क्षेत्र में किया जाता है।
- नाभिकीय विखण्डन की अनियन्त्रित श्रृंखला अभिक्रिया द्वारा परमाणु बम का निर्माण किया जाता है जिसका उपयोग युद्ध के क्षेत्र में किया जाता है।
प्रश्न 25.
नाभिकीय रियेक्टर के कोई तीन उपयोग लिखो।
उत्तर:
नाभिकीय रियेक्टर के निम्नलिखित उपयोग होते हैं-
- विद्युत ऊर्जा उत्पादन में
- विखण्डीय पदार्थों को बनाने में।
- नाभिकीय शोध कार्यों में।
प्रश्न 26.
नाभिकीय रियेक्टर का सिद्धान्त समझाइये।
उत्तर:
नाभिकीय रियेक्टर ऊष्मा रूपान्तर के सिद्धान्त पर कार्य करता है। नाभिकीय रियेक्टर कंक्रीट की मोटी दीवारों से बना होता है। इसमें एक स्टील पात्र में नियन्त्रित नाभिकीय विखण्डन की क्रिया (क्रांतिक नाभिकीय अभिक्रिया) द्वारा अत्यधिक मात्रा में ऊष्मीय ऊर्जा उत्पन की जाती है। इस ऊष्मीय ऊर्जा से जल को वाष्पित करके उसकी भाप से टरबाइन चलाया जाता है। टरबाइन के अपने या डायनमो की कुण्डली भी घूमने लगती है जिससे विद्युत ऊर्जा ऊर्जा उत्पन्न होती है। इसका उपयोग विभिन्न रचनात्मक कार्यों के लिए किया जाता है।
प्रश्न 27.
नाभिकीय विखण्डन से क्या अभिप्राय है?
उत्तर:
नाभिकीय विखण्डन-यह वह नाभिकीय अभिक्रिया है जिसमें एक भारी नाभिक दो लगभग समान आकार के हल्के नाभिक खण्डों में टूट जाता है तथा दो या तीन नये न्यूट्रॉन, X किरणें उत्सर्जित होती हैं और अत्यधिक ऊर्जा विमोचित होती है। अतः नाभिकीय विखण्डन से अभिप्राय उस नाभिकीय ऊर्जा स्रोत से है जिसमें एक भारी अस्थायी नाभिक, खण्डित होता हुआ दो या तीन न्यूट्रॉन के साथ अत्यधिक परिमाण में ऊर्जा विमोचित करती है।
प्रश्न 28.
नाभिकीय ऊर्जा क्या है? इसके दो शान्तिपूर्ण उपयोग लिखिए।
उत्तर:
नाभिकीय संलयन तथा नाभिकीय विखण्डन क्रिया में मुक्त ऊर्जा ही नाभिकीय ऊर्जा है। इसका शान्तिपूर्ण उपयोग है-
- विद्युत ऊर्जा के उत्पादन में।
- चिकित्सा क्षेत्र में कैंसर रोग के इलाज में।
प्रश्न 29.
नाभिकीय अभिक्रिया तथा रासायनिक अभिक्रिया में प्रमुख अन्तर क्या हैं? लिखिए।
उत्तर:
नाभिकीय अभिक्रिया तथा रासायनिक अभिक्रिया में प्रमुख अन्तर निम्नलिखित हैं-
| नाभिकीय अभिक्रिया | रासायनिक अभिक्रिया |
| 1. इस अभिक्रिया में परमाणु के नाभिक भाग लेते हैं जिनका विखण्डन या संलयन होता है। | 1. इस अभिक्रिया में परमाणु के बाह्यतम कक्षा के इलेक्ट्रॉन भाग लेते हैं। |
| 2. इस अभिक्रिया में परमाणु संयोजित होकर पुनः व्यवस्थित नहीं होते। | 2. इस अभिक्रिया में परमाणु केवल विभिन्न प्रकार से संयोजित होकर पुन: व्यवस्थित हो जाते हैं। |
| 3. इस अभिक्रिया में नये कणों तथा नाभिकों का निर्माण होता है। | 3. इस अभिक्रिया में नए परमाणु का निर्माण होता है। |
| 4. इस अभिक्रिया के फलस्वरूप अत्यधिक मात्रा में ऊर्जा उत्पन्न होती है। | 4. इस अभिक्रिया के फलस्वरूप बहुत कम मात्रा में ऊर्जा उत्पन्न या अवशोषित होती है। |
प्रश्न 30.
ऊर्जा संकट क्या है? ऊर्जा संकट के दो कारण लिखिए।
उत्तर:
ऊर्जा के प्रमुख प्राकृतिक स्रोतों जैसे- कोयला, पेट्रोलियम एवं प्राकृतिक गैस की मात्रा पृथ्वी पर सीमित है। इंजन के आविष्कार से लेकर आज तक इन्हीं ऊर्जा संसाधनों पर हम निर्भर करते हैं। चूँकि ये दुर्लभ तथा अनवीकरणीय ऊर्जा स्रोत हैं जिसका दोहन इतनी अधिक दर से हो रहा है कि ये अतिशीघ्रता से समाप्त हो सकते है, फलस्वरूप भविष्य में ऊर्जा प्राप्त न हो सकने की अर्शिका से संसार में एक प्रकार का भय व्याप्त हो गया है इस परिस्थिति को ही ऊर्जा संकट कहते हैं।
उक्त ऊर्जा संकट के कारण –
- जनसंख्या में अत्यधिक के कारण अनवीकरणीय ऊर्जा स्रोतों का अत्यन्त दोहन किया जाता है।
- कम दक्षता वाली मशीनों के उपयोग के कारण ऊर्जा के अधिकांश भाग का ह्रास होना।
प्रश्न 31.
सागरीय तापीय ऊर्जा किसे कहते हैं?
उत्तर:
महासागर की सतह के जल तथा गहराई में स्थित जल के ताप में सदैव अन्तर होता है। कई स्थानों पर यह अन्तर 20°C तक हो सकता है। इस रूप में उपलब्ध ऊर्जा को सागरीय तापीय ऊर्जा (Ocean Ther- mal Energy ) या संक्षिप्त में OTE कहते हैं सागरीय तापीय ऊर्जा को विद्युत जैसे उपयोगी रूप में परिवर्तित किया जा सकता है।

प्रश्न 32.
ज्वारीय तरंगें किस प्रकार उत्पन्न होती हैं?
उत्तर:
सागरीय ऊर्जा एक अन्य रूप में भी उपलब्ध होती है और वह है- सागरीय लहरों से सम्बद्ध ऊर्जा। सागर की सतह पर चलने वाली वायु की तीव्र धाराओं से उत्पन्न ऊँची-ऊँची लहरें निरंतर तट पर ऊपर-नीचे उठती- गिरती रहती हैं। ऊँची-ऊँची लहरें निरंतर तट पर टकराती हैं, तो यह लहरें ज्वारीय तरंगें कहलाती हैं।
प्रश्न 33.
पवन चक्की का कार्यकारी सिद्धान्त लिखिए। अथवा पवन चक्की का सिद्धान्त स्पष्ट करें।
उत्तर:
जब पवन चक्की के ब्लेडों से वायु टकराती है, तो उन पर एक बल लगता है, जिससे पवन चक्की घूमने लगती है। पवन चक्की का घूर्णन उसके ब्लेडों की विशिष्ट बनावट के कारण सम्भव होता है, जो किसी विद्युत पंखों के ब्लेडों के समान ही होती है जिस प्रकार विद्युत पंखे के ब्लेडों के घूमने से वायु गतिशील हो जाती है, ठीक इसी प्रकार गतिशील वायु पंखे को घुमाती है। पवन चक्की द्वारा कुएँ या खदानों में भरे पानी को बाहर निकाला जा सकता है या विद्युत उत्पन्न की जा सकती है।
प्रश्न 34.
सौर ऊर्जा का विद्युत ऊर्जा में रूपान्तरण करने की किसी एक युक्ति का वर्णन कीजिए। अथवा सौर सेल पैनल का वर्णन कीजिए एवं उपयोगिता लिखिए
उत्तर:
सौर ऊर्जा को विद्युत ऊर्जा में परिवर्तित करने के लिए सौर सेल या सौर पैनल प्रयुक्त करते हैं।
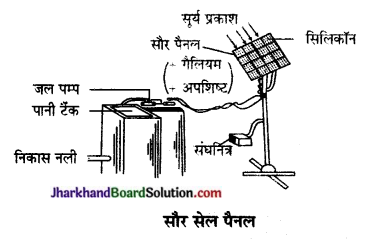
सौर सेल पैनल – सौर सेल प्रकाश-विद्युत प्रभाव के सिद्धान्त पर कार्य करती है जो सीधे ही सौर ऊर्जा को विद्युत ऊर्जा में रूपान्तरित कर देती हैं सौर सेल की दक्षता कम होने के कारण अनेक सौर सेलों को विशेष क्रम में व्यवस्थित कर दिया जाता है जिससे विभिन्न कार्यों के लिए पर्याप्त परिमाण में विद्युत ऊर्जा प्राप्त की जा सकती है सौर सेलों की यह व्यवस्था सौर सेल पैनल कहलाती है। सौर पैनल से सौर सेलों को जोड़ने के लिए चाँदी का प्रयोग किया जाता है सौर पैनल में निर्मित विद्युत दिष्ट धारा होती है।
सौर सेल पैनल की उपयोगिता –
- इसका उपयोग कृत्रिम उपग्रहों तथा अंतरिक्षयानों में विद्युत उपलब्ध करने हेतु किया जाता है।
- दूरस्थ वन ग्रामों की सड़कों पर प्रकाश करने. सिंचाई के लिए जलपंपों को चलाने तथा रेडियो एवं टेलीविजन सेटों को चलाने किया जाता है।
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
प्रकाश ऊर्जा का अवशोषण किन-किन रूपों में होता है? समझाइये।
उत्तर:
जब प्रकाश ऊर्जा पृथ्वी के वायुमण्डल से होकर गुजरती है तो उनमें से केवल 47% ऊर्जा ही पृथ्वी सतह तक पहुँचती है, शेष ऊर्जा वायुमण्डल में अवशोषित एवं कुछ परावर्तित हो जाती है।
प्रकाश ऊर्जा का अवशोषण निम्नलिखित रूपों में होता है-
(1) पराबैंगनी प्रकाश का अवशोषण प्रकाश की पराबैंगनी किरणें लगभग पूरी तरह वायुमण्डल की ओजोन परत द्वारा अवशोषित कर ली जाती हैं।
(2) अवरक्त प्रकाश का अवशोषण- पृथ्वी की सतह द्वारा अवरक्त प्रकाश अवशोषित की जाती है ये अवरक्त प्रकाश अपने मार्ग में आने वाली सभी वस्तुओं को गर्म कर देता है। फलस्वरूप पृथ्वी सतह के जल तथा पृथ्वी की सतह को गर्म कर देती है अर्थात् अवरक्त प्रकाश ऊष्मा के रूप में पृथ्वी के विभिन्न घटकों द्वारा अवशोषित कर ली जाती है। अप्रत्यक्ष रूप से सौर ऊर्जा का अवशोषण महासागरीय ऊर्जा का पवन ऊर्जा के रूप में होता है।
(3) दृश्य प्रकाश का अवशोषण-पौधों में रासायनिक ऊर्जा के रूप में दृश्य प्रकाश का अवशोषण होता है जो जैव द्रव्यमान में परिवर्तन द्वारा जीवाश्म ईंधन के रूप में प्राप्त होता है। पौधों एवं जन्तुओं में भोजन के रूप में अवशोषण सतत होता रहता है। कुछ भाग वायुमण्डल में उपस्थित जल वाष्प, ओजोन परत, धूल कण तथा CO2 द्वारा अवशोषित कर लिया जाता है।
प्रश्न 2.
सौर तापन युक्तियाँ किसे कहते हैं? सौर कुकर का वर्णन निम्न शीर्षकों में करें-
(i) सिद्धान्त
(ii) नामांकित रेखाचित्र,
(iii) कार्यविधि
उत्तर:
सौर तापन युक्ति- वे युक्तियाँ जो सूर्य से प्राप्त ऊर्जा का अधिक से अधिक संग्रह कर सकें तथा संगृहित ऊष्मा का क्षय कम-से-कम करें, सौर तापन युक्तियाँ कहलाती हैं।
सौर कुकर का वर्णन-
(i) सिद्धान्त- काले रंग की सतह पर परावर्तक सतह की तुलना में अधिक ऊष्मा का अवशोषण होता है इसलिए सौर कुकर में काली सतह का उपयोग करके उसे ऊष्मारोधी बॉक्स में रखकर उसकी ऊपरी सतह को किसी काँच की पट्टी से बैंक दिया जाता है जिससे काली सतह द्वारा ऊष्मा का अधिक अवशोषण तथा कम-से-कम व्यय होता है फलस्वरूप उसका आन्तरिक भाग अत्यधिक गर्म हो जाता है।
(ii) नामांकित रेखाचित्र-
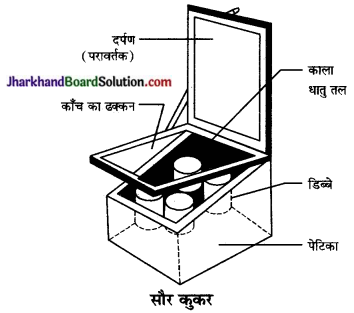
(iii) कार्यविधि – काले रंग से पुता ऐलुमिनियम के बर्तन में वह खाद्य पदार्थ रख देते हैं जिसे पकाना है। यह बर्तन कुकर के अन्दर रखकर समतल कांच के ढक्कन द्वारा ढक देते हैं अब सौर कुकर को सूर्य के प्रकाश में इस प्रकार व्यवस्थित करके रख देते हैं कि का प्रकाश समतल दर्पण से परावर्तित होकर कुकर अन्दर प्रवेश करे।
पेटिका के अन्दर एवं बर्तनों के बाहर काला रंग ऊष्मा को अवशोषित करता है। पेटिका के ऊपर रखी समतल कौन की प्लेट ग्रीन हाउस प्रभाव उत्पन्न करती है जिससे बॉक्स के अन्दर का ताप 2-3 घण्टे में लगभग 100°C से 140- तक पहुँच जाता है और बर्तन में रखा खाद्य पदार्थ पक जाता है।
प्रश्न 3.
अर्द्धचालक क्या? सौर सेल के कार्य सिद्धान्त की व्याख्या कीजिए।
उत्तर:
अर्द्धचालक- अर्द्धचालक वे पदार्थ होते हैं जो सामान्यतः विद्युत के सुचालक नहीं होते किन्तु इनमें कुछ विशेष अपद्रव्य मिला दिये जायें तो उनकी चालकता बढ़ जाती है। इन पर प्रकाश पड़ने से इनकी विद्युत चालकता और बढ़ जाती है जैसे- सिलिकॉन तथा गैलियम।
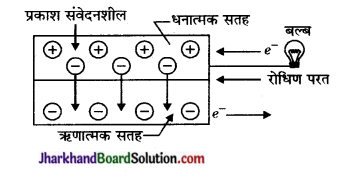
सौर सेल का कार्य सिद्धान्त-सौर सेल प्रायः अपद्रव्य मिश्रित अर्द्धचालक पदार्थ की परतों से बना होता है। जब इन परतों पर सूर्य का प्रकाश पड़ता है तो अर्द्धचालक के दो भागों में विभवान्तर उत्पन्न हो जाता है। अर्द्धचालक से मुक्त हुए इलेक्ट्रॉनों के कारण इसमें धारा प्रवाहित होने लगती है। 4 वर्ग सेण्टीमीटर साइज के किसी सौर सेल द्वारा 60 मिली ऐम्पियर धारा लगभग 0.4-0.5V पर उत्पन्न होती है। इस अर्द्धचालकों से निर्मित सौर सेलों की दक्षता 10-18% है जबकि आधुनिक सेलेनियम सोलर सेल की दक्षता 25% तक है।
प्रश्न 4.
पवन के प्रवाहित होने के कारणों की व्याख्या कीजिए।
उत्तर:
पवन के प्रवाहित होने के लिए निम्नलिखित कारण उत्तरदायी हैं-
- पृथ्वी की अपनी अक्ष के परितः घूर्णन गति।
- पृथ्वी के भूमध्य रेखीय भाग का ताप अधिक व ध्रुवों के पास का ताप कम होना।
- स्थानीय संवहन धाराएँ।
पृथ्वी के भूमध्य रेखीय भागों पर सूर्य की किरणें सीधे आपतित होती हैं जबकि ध्रुवीय भागों पर सूर्य की किरणें तिरछी आपतित होती हैं अतः भूमध्य रेखीय भागों में पृथ्वी तल के समीप की वायु ध्रुवीय भागों की अपेक्षा अतिशीघ्र तथा अधिक गर्म हो जाती हैं, इसके फलस्वरूप पृथ्वी पर संवहन धाराएँ बन जाती हैं तथा भूमध्य रेखीय भांगों की वायु अधिक गर्म होने के कारण ऊपर उठने लगती है।
इनके खाली स्थान को भरने के लिए ध्रुवीय स्थानों की अपेक्षाकृत ठण्डी वायु भूमध्यरेखीय भाग की और बहने लगती है। वायु के इस प्रवाह में पृथ्वी के घूर्णन तथा स्थानीय संवहन धाराओं के कारण लगातार बाधा पड़ती रहती है, इसी का परिणाम है-पवन। ये मंद वेग पवन से लेकर विनाशकारी टारनेडो तक परिवर्तित हो सकती हैं।

प्रश्न 5.
जल विद्युत उत्पादन को सचित्र समझाइये।
उत्तर:
जल विद्युत उत्पादन- आजकल नदियों में प्राकृतिक रूप से बहते हुए पानी की गतिज ऊर्जा को बाँध बनाकर स्थितिज ऊर्जा के रूप में संचित कर लिया जाता है जिससे विद्युत संयंत्र द्वारा विद्युत उत्पादित की जाती है।
बाँध के उच्च स्तर से जल को पाइपों द्वारा उसके तली के पास लगाये गये जल विद्युत संयंत्र (विद्युत जनित्र) तक गिराया जाता है। इससे जल की स्थितिज ऊर्जा गिरते हुए पानी की गतिज ऊर्जा में परिवर्तित हो जाती है। पाइप से गिरता हुआ पानी टरबाइनों को घुमाता है जो विद्युत जनित्रों में आर्मेचर को घुमाती है, आर्मेचर के घूमने से विद्युत उत्पादित होती है। इस पूरे प्रक्रम में ऊर्जा का रूपान्तरण निम्न प्रकार होता है-बाँध में भंडारित जल की स्थितिज ऊर्जा गिरते हुए पानी की गतिज ऊर्जा में रूपांतरित होती है। ये ऊर्जा टरबाइन में घूर्णन गति उत्पन्न करता है। जनरेटर इस गतिज ऊर्जा को विद्युत ऊर्जा में रूपान्तरित कर देता है।
प्रश्न 6.
सौर जल ऊष्मक का वर्णन निम्नांकित शीर्षकों में कीजिए – (i) सिद्धान्त, (ii) उपकरण का रेखाचित्र, (iii) कार्यविधि।
उत्तर:
सौर जल ऊष्मक-सौर जल ऊष्मक एक ऐसी युक्ति है जिसमें सौर ऊर्जा का उपयोग करके ठण्डे जल से गर्म जल प्राप्त किया जाता है।
(i) सिद्धान्त-सौर जल ऊष्मक में सौर ऊर्जा का रूपान्तरण ऊष्मा ऊर्जा के रूप में होता है जब सूर्य का प्रकाश संग्राहक पर पड़ता है तो इसके काले रंग में रंगे ताँबे की सर्पिलाकार नली अवरक्त किरणें अवशोषित कर ऊष्मा उत्पन्न करती है। यह ऊष्मा पानी को गर्म कर देती है।
(ii) उपकरण का रेखाचित्र-
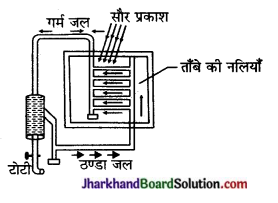
(iii) कार्यविधि – चित्र में सौर जल ऊष्मक प्रदर्शित है। सौर जल ऊष्मक को छत पर खुले स्थान में इस प्रकार स्थायी रूप से व्यवस्थित कर दिया जाता है कि सूर्य से आने वाली अधिक-से-अधिक किरणें सीधे इस पर पड़ें।
सूर्य से आने वाली किरणें जब ताँबे की नलियों की काली सतह पर पड़ती हैं तो ये सतह ऊष्मा को अवशोषित कर लेती हैं। चूँकि ताँबा, ऊष्मा का सुचालक है, अतः शीघ्र ही यह अवशोषित ऊष्मा नलियों में बहने वाले जल को मिल जाती है जिससे जल में संवहन धारायें बन जाती हैं तथा गर्म जल ऊपर उठकर गर्म जल संग्राहक में चला जाता है और ठण्डा जल नीचे नलियों में आ जाता है, यह प्रक्रम चलता रहता है और गरम जल टोंटी से प्राप्त होता रहता है।
प्रश्न 7.
प्रकाश ऊर्जा का अवशोषण किन-किन रूपों में तथा किस प्रकार होता है? समझाइए। अथवा सौर ऊर्जा का सजीवों में अधिग्रहण एवं स्थानान्तरण प्रक्रम को सचित्र समझाइये।
उत्तर:
सूर्य से ऊर्जा का प्रवाह शुरू होता है। हरे पौधे प्रकाश संश्लेषण प्रक्रिया द्वारा इस सौर ऊर्जा को अंतर्ग्रहण करते हैं। सौर ऊर्जा अजैव वातावरण के माध्यम से जीवों में प्रवेश करती है। केवल वही पौधे सौर ऊर्जा को अंतर्ग्रहण करते हैं, जिनमें क्लोरोफिल नामक हरित वर्णक होता है। इस ऊर्जा को अंतर्ग्रहण करने के पश्चात् पौधे इसे रासायनिक ऊर्जा में परिवर्तित कर देते हैं जो कार्बोहाइड्रेट के रूप में संगृहित हो जाती है। इस ऊर्जा का कुछ अंश पौधे अपनी वृद्धि तथा ऊतकों के निर्माण में उपयोग करते हैं तथा जो ऊर्जा उपयोग नहीं होती, वह ऊष्मा के रूप में मुक्त हो जाती है।
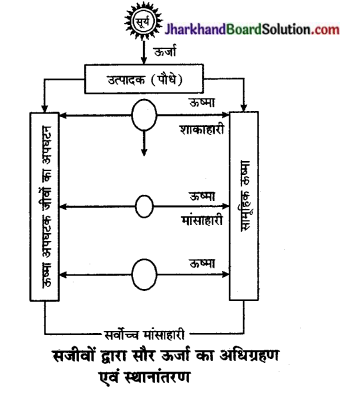
शाकाहारी जन्तु इन पौधों को भोजन के रूप में खाते हैं। शाकाहारी जन्तुओं को मांसाहारी तथा मांसाहारी जन्तुओं को सर्वोच्च मांसाहारी खाते हैं। पौध एवं प्राणियों के मृत शरीर को अपघटक जीवाणु अपना भोजन बनाते हैं तथा उन्हें अपघटित कर खाद के समान उपयोगी बनाते हैं। इस प्रकार हरे पौधों द्वारा सर्वप्रथम सौर ऊर्जा का अधिग्रहण किया जाता है तत्पश्चात् अन्य सजीवों में ऊर्जा का स्थानान्तरण खाद्य श्रृंखला के द्वारा होता है।
प्रश्न 8.
सौर ऊर्जा का विद्युत ऊर्जा में रूपान्तरण करने का वर्णन कीजिए तथा सौर सेल पैनल की उपयोगिता लिखिए।
उत्तर:
सौर सेल एक ऐसी युक्ति है, जो सौर ऊर्जा को विद्युत ऊर्जा में परिवर्तित करती है। लगभग 100 वर्ष पहले यह खोज की जा चुकी थी कि सेलेनियम की किसी पतली पर्त को सौर प्रकाश में रखने पर विद्युत उत्पन्न होती है। यह भी ज्ञात था कि सेलेनियम के किसी टुकड़े पर आपतित सौर ऊर्जा का केवल 0.6 प्रतिशत ही विद्युत में परावर्तित हो पाता है। चूँकि इस प्रकार के सौर सेल की दक्षता बहुत कम थी, इसलिए विद्युत उत्पन्न करने के लिए इस परिघटना का उपयोग करने के कोई विशेष प्रयत्न नहीं किए गए।
सबसे पहला व्यावहारिक सौर सेल सन् 1954 में बनाया गया था। यह सेल लगभग 1.0 प्रतिशत सौर ऊर्जा को विद्युत ऊर्जा में परिवर्तित कर सकता था। आजकल अर्द्धचालकों से निर्मित सौर सेल द्वारा कहीं अधिक दक्षता प्राप्त की जा चुकी है। अंतरिक्ष कार्यक्रमों द्वारा उत्पन्न बढ़ती हुई माँग के कारण भी अधिक-से-अधिक दक्ष सौर सेलों को विकसित करने की दर में वृद्धि हुई है। आधुनिक सेलेनियम सौर सेल की दक्षता 25% तक है, जबकि अर्द्ध- चालकों से निर्मित सौर सेलों की दक्षता 10-18% है।
आजकल प्रायः सौर सेल, सिलिकॉन तथा गैलेनियम जैसे अर्द्धचालकों से बनाए जाते हैं अर्द्धचालक ऐसे पदार्थ हैं, जिनमें सामान्यतः विद्युत प्रवाहित नहीं की जा सकती है अर्थात् वे सुचालक नहीं होते किन्तु विद्युतरोधियों की तुलना में इनमें कुछ सीमा तक विद्युत का चालन सम्भव है परन्तु यदि अर्द्धचालकों में कुछ विशेष अपद्रव्य मिला दिया जाए तो उनकी चालकता अर्थात् विद्युत चालन की सामर्थ्य अभूतपूर्व रूप से बढ़ जाती है।
प्रकाश पड़ने पर भी अर्द्धचालकों की चालकता बढ़ जाती है। सौर सेल में अपद्रव्य मिश्रित अर्द्धचालकों की परतें इस प्रकार व्यवस्थित की जाती हैं कि प्रकाश पड़ने पर अर्द्धचालक के दो भागों में विभवान्तर उत्पन्न हो जाए। 4 वर्ग सेमी साइज के किसी सौर सेल द्वारा 60 मिली ऐम्पीयर धारा लगभग 0.4-0.5V पर उत्पन्न होती है। किस सौर सेल पैनल में अनेक सौर सेल विशेष क्रम में व्यवस्थित होते हैं, उसमें विभिन्न कार्यों के लिए कति परिमाण में विद्युत प्राप्त की जा सकती है।
सौर सेल पैनल की उपयोगिता – सौर सेलों का उपयोग दुर्गम तथा दूरस्थ स्थानों में अत्यन्त प्रभावशाली सिद्ध हुआ है। समस्त कृत्रिम उपग्रहों तथा अन्तरिक्ष अन्वेषक चिनि मुख्यतः सौर पैनलों द्वारा उत्पादित विद्युत पर निर्भर करते हैं। भारत में सौर सेलों का उपयोग प्रकाश व्यवस्था में तथा जल पम्पों, रेडियो तथा दूरदर्शन के अभिग्राहियों को प्रचलित करने के लिए किया गया है। इसके अतिरिक्त इनका उपयोग द्वीप स्तम्भों (Light houses) में तथा तट से दूर निर्मित खनिज तेल के कुएँ खोदने के रिंग को विद्युत ऊर्जा प्रदान करने में भी होता है।
प्रश्न 9.
जैव मात्रा किसे कहते हैं?
उत्तर:
वनस्पतियों एवं जंतुओं के शरीर में स्थित पदार्थों को जीव द्रव्यमान (मात्रा) कहते हैं किसी जीव की के बाद जीव द्रव्यमान का उपयोग घरेलू ईंधन के रूप में किया जा सकता है। वास्तव में लकड़ी कृषि अपशिष्ट तथा गोबर के कण्डे सब मिलाकर गाँवों की ऊर्जा की आवश्यकता का 80% अंश प्रदान करते हैं।
चूँकि गोबर के कण्डों का दहन अपूर्ण होता है तथा वे अत्यधिक धुआँ उत्पन्न करते हैं, इसलिए ईंधन के रूप में इनके प्रयोग न केवल लाभप्रद तत्त्व नष्ट होते हैं, अपितु इनसे वातावरण भी प्रदूषित होता है इसलिए गोबर के कण्डों को सीधा जलाना अविवेकपूर्ण है। इसके स्थान पर गोबर को गोबर गैस में परिवर्तित करना चाहिए, जो एक साफ-सुथरा ईंधन है गोबर गैस बनाने के बाद बचे अवशेष में अत्यधिक पोषक तत्त्व होते हैं, जिसे खाद के रूप में उपयोग किया जाता है।
प्रश्न 10.
अन्तः दहन इंजन किसे कहते हैं? इसकी रचना एवं कार्यविधि समझाइए।
उत्तर:
अन्तः दहन इंजन- इस इंजन में ईंधन की अल्प मात्रा सिलिण्डर में डालकर प्रज्वलित की जाती है। दहन के दौरान निकली गैसों के द्वारा उत्पन्न दाब पिस्टन को बाहर धकेलता है। किसी निश्चित समय में सिलिण्डर के अन्दर केवल थोड़ी-सी मात्रा में ईंधन जलते हैं, इसलिए इसे अन्त: दहन इंजन कहते हैं। अन्त: दहन इंजन का आविष्कार रूडोल्फ डीजल तथा निकोलस आटो ने किया था।
अन्तः दहन इंजन का सिद्धान्त (Principle of In ternal Combustion Engine ) – इस इंजन द्वारा बहुत अल्प मात्रा में ईंधन को सिलिण्डर में प्रज्वलित किया जाता है इस दहन द्वारा निकली गैसों से उत्पन्न दाब द्वारा पिस्टन को बाहर की तरफ धकेलकर उसे गतिशील बनाया जाता है।
अन्तः दहन इंजन की रचना तथा विधि – अन्त: दहन इंजन में एक समय पर बहुत ही अल्प मात्रा में ईंधन को सिलिण्डर में जलाया जाता है। इसी इंजन को सुविधानुसार छोटे आकार में बनाया जाता है। इस इंजन में ईंधन को जलाकर गैसों में परिवर्तित करना तभी गैसों के दबाव से पिस्टन को गतिशील बनाना निम्न चरणों में पूर्ण होता है-
- अन्तर्ग्रहण – सर्वप्रथम ईंधन की अल्प मात्रा तथा वायु का मिश्रण सिलिण्डर में प्रविष्ट कराया जाता
- सम्पीडन – ईंधन तथा वायु के मिश्रण को सम्पीडित किया जाता है।
- दहन – मिश्रण को प्रज्वलित किया जाता है।
- विस्तारण प्रज्वलन के कारण अत्यधिक मात्रा में ऊष्मा उत्पन्न होती है जो दहन के समय निकली गैसों को प्रसारित करती है गैसों के प्रसारण से बल उत्पन्न होता है, जो पिस्टन को बाहर धकेलता है।
- निर्गम – अन्त में निर्गम वाल्व के खुलने से दहन के उपोत्पाद बाहर निकाल दिये जाते हैं।
प्रश्न 11.
स्थायी गुम्बज प्रकार के बायोगैस संयन्त्र का नामांकित चित्र सहित वर्णन कीजिए।
उत्तर:
दो प्रकार के बायोगैस संयन्त्र प्रचलन में हैं-
- स्थिर गुम्बदनुमा टंकी वाले बायोगैस संयन्त्र।
- प्लावित (तैरती हुई) टंकी वाले बायोगैस संयन्त्र।
स्थिर गुम्बदनुमा टंकी वाले बायोगैस संयन्त्र मुख्य भाग निम्न प्रकार हैं- (a) संपाचक ( टैंक), (b) मिलाने का टैंक, (c) निर्गम टैंक, (d) गुम्बदनुमा टैंक।
(a) संपाचक – यह एक स्टील का या कंक्रीट का बेलनाकार टैंक होता है, जिसका व्यास आवश्यकतानुसार रखा जाता है, यह जमीन के अन्दर या ऊपर बनाया जाता है।
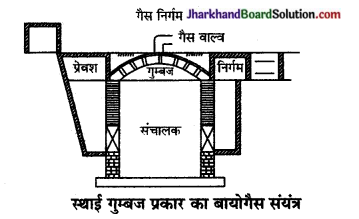
(b) मिलाने का टैंक व
(c) निर्गम टैंक-संपाचक से दो अन्य छोटे-छोटे टैंक सम्बन्धित रहते हैं, जिनमें एक है मिलाने का टैंक, जिसमें गोबर या अन्य अपशिष्ट पदार्थों का घोल डाला जाता है व दूसरा निर्गम टैंक, जिसमें स्लरी
(बचा हुआ घोल) एकत्र होता रहता है।
(d) गुम्बदनुमा टंकी – यह संपाचक के ऊपर स्थिर रहती है तथा इनमें बायोगैस एकत्र होती रहती है जैसा कि चित्र में प्रदर्शित है।
प्रश्न 12.
समुद्रीय तरंगें कैसे बनती हैं?
उत्तर:
समुद्री तरंगों की उत्पत्ति का कारण है- जल की सतह के नीचे गहराइयों में तापान्तर, जो ध्रुव प्रदेशों व भूमध्य रेखा पर स्थित बिन्दुओं के बीच उत्पन्न होता है तथा एक ही स्थान पर तल की ऊपरी तह व नीचे की तहाँ के बीच स्थापित होता है। इस तापान्तर के कारण भूमध्य रेखीय समुद्र की सतह का गर्म जल ध्रुवों की ओर बहने लगता है। क्योंकि वह हल्का, पतला व प्रवाहशील होता है। ध्रुवीय प्रदेशों का जल परिणामस्वरूप भूमध्य रेखा की ओर प्रवाहित होने लगता है। वायु प्रवाह तथा पृथ्वी की घूर्णन गति के कारण इसका मार्ग निर्दिष्ट होता है।
प्रश्न 13.
हवा क्यों चलती है?
उत्तर:
सूर्य द्वारा विकिरित ऊष्मा आकाश व वायुमण्डल में से होकर पृथ्वी तक पहुँचती है, किन्तु वायुमण्डल की वायु को यह गर्म नहीं करती। पृथ्वी पर ठोस धरातल तथा महासागरों के जल की सतह द्वारा इस ऊष्मा का अवशोषण होता है, जिससे दोनों सतहों के ताप में वृद्धि होती है। ताप में यह वृद्धि सभी स्थानों पर एक समान नहीं होती। भूमध्य रेखीय कटिबन्ध (क्षेत्र) में ताप वृद्धि ध्रुवीय क्षेत्रों की तुलना में (जल तथा थल) दोनों में अधिक रहती है। यह तापान्तर ही वह प्रमुख कारण है, जिसके होने से वायु प्रवाह होता है और आँधियाँ आती हैं।

प्रश्न 14.
मानसून किसे कहते हैं?
उत्तर:
मानसून के कारण पृथ्वी पर वर्ष के अर्द्ध- भाग में थल की सतह जल सतह की अपेक्षा अधिक उष्ण हो जाती है, तब समुद्र की सतह के ऊपर की वाष्प सन्तृप्त वायु की ओर प्रवाहित होती है। इसके कारण पृथ्वी पर लम्बी अवधि तक वर्षा होती रहती है। वर्ष के अर्द्धभाग में यह क्रिया विपरीत दिशा में होती है, तब वायु पृथ्वी की ओर से समुद्र की ओर बहती है। इसी कारण मानसून उठता है तथा यही दोनों मानसून कहलाते हैं।
पृथ्वी पर एवं सागर तल पर सूर्य ताप के कारण वाष्पन की क्रिया सतत होती रहती है। यही वाष्प बादल बन जाती है तथा बादल ठण्डक पाकर वर्षा करते हैं। इस प्रकार जल वाष्प चक्र निरन्तर चलता रहता है।
प्रश्न 15.
वायु ऊर्जा, पवन चक्की तथा सौर ऊर्जा के तीन उपयोग बताइए जल ऊर्जा का एक उपयोग लिखो।
उत्तर:
वायु ऊर्जा के उपयोग-
- पवन चक्कियों को चलाने में।
- भूमिगत पानी को बाहर निकालने में।
- विद्युत के उत्पादन में।
पवन चक्की के उपयोग-
- मक्का तथा गेहूँ आदि पीसने में
- इसके द्वारा टरबाइन चलाकर विद्युत ऊर्जा उत्पादित की जा सकती है।
- इस चक्की के उपयोग से खदानों में भरा पानी निकाला जा सकता है।
सौर ऊर्जा के उपयोग-
- सौर ऊर्जा द्वारा विद्युत ऊर्जा प्राप्त की जाती
- सौर ऊर्जा का उपयोग (सोलर कुकर द्वारा) ख्भना पकाने में किया जाता है।
- सौर ऊर्जा को ऊष्मीय ऊर्जा में परिवर्तित क्रकरे प्राप्त ऊर्जा से पानी गर्म करना, हीटर चलाना आदि क्रियाएँ कर सकते हैं।
जल ऊर्जा के उपयोग-विद्युत उत्पादन में।
प्रश्न 16.
बाह्ल दहन इंजन और अन्तःदहन इंजन में अन्तर स्पष्ट कीजिये।
उत्तर:
बाह्य दहन इंजन और अन्तःदहन इंजन में निम्नलिखित अन्तर हैं-
| बाट़ा दहन इंजन | अन्तः ढहन इंजन |
| 1. इसमें सिलेण्डर के बाहर ईंधन का दहन होता है। | 1. इसमें सिलेण्डर के अन्दर ईंधन का दहन होता है। |
| 2. पिस्टन जल-वाष्प के दाब से गतिशील होता है। | 2. पिस्टन गैसीय दाब के कारण गतिशील होता है। |
| 3. इसमें वाष्प बनाने के लिए बॉयलर का उपयोग होता है। | 3. इसमें बॉयलर का कोई उपयोग नहीं होता है। |
| 4. इसमें प्रदूषण नहीं होता। | 4. इसमें प्रदूषण होता है। |
प्रश्न 17.
जल विद्युत का उत्पादन कैसे करते हैं?
उत्तर:
पानी को ऊँचे स्थानों पर (बाँध द्वारा) एकत्रित किया जाता है। इस प्रकार पानी में स्थितिज ऊर्जा संग्रहीत होती है। जब इस पानी को नीचे गिराया जाता है, तो स्थितिज ऊर्जा गतिज ऊर्जा में रूपान्तरित होती है, इस गतिज ऊर्जा को यांत्रिक ऊर्जा में बदलकर टरबाइन चलाए जाते हैं। इस प्रकार टरबाइन से प्राप्त यांत्रिक ऊर्जा को विद्युत उत्पादक यंत्रों (विद्युत जनित्र ) द्वारा विद्युत ऊर्जा में परिवर्तित किया जाता है। इसका एक उदाहरण भाखड़ा बाँध है। बहुत पहले गतिशील पानी की गतिज ऊर्जा का प्रयोग पवन चक्कियों को चलाने में करते थे, जिससे गेहूँ आदि पीसा जाता था।
प्रश्न 18.
नवीकरण और अनवीकरण स्त्रोतों से आप क्या समझते हो? उदाहरण सहित लिखो।
उत्तर:
- नवीकरण स्त्रोत – वे स्रोत, जिनमें एक निश्चित समय के बाद पुनः प्रकट होने की क्षमता होती है, नवीकरण स्रोत कहे जाते हैं।
- उदाहरण – मिट्टी, जल और जैविक समुदाय।
- अनवीकरण स्त्रोत – वे खोत, जिनमें पुनर्चक्रण या पुनर्स्थापना की क्षमता नहीं होती, अनवीकरण खोत कहे जाते हैं।
- उदाहरण – जीवाश्म ईंधन-जैसे कोयला, पेट्रोलियम एवं खनिज आदि।
प्रश्न 19.
तैरती हुई गैस टंकी वाले बायोगैस संयन्त्र का सचित्र वर्णन कीजिए।
उत्तर:
तैरती हुई टंकी वाले बायोगैस संयन्त्र – इस प्रकार के गैस संयंत्र में सभी भाग गुम्बदनुमा टंकी वाले बायोगैस संयन्त्र के समान ही होते हैं। इसकी गैस संग्राहक टंकी संपाचक के ऊपर तैरती रहती है।
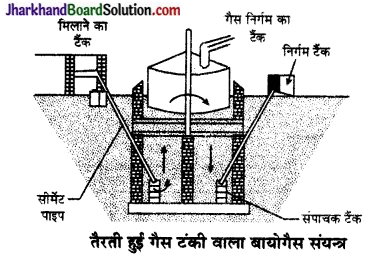
चित्र-तैरती हुई गैस टंकी वाला बायोगैस संयन्त्र
इसके प्रमुख भाग निम्नलिखित हैं-
- जल तथा गोबर मिश्रण के लिए प्रवेश मार्ग
- मुख्य टैंक
- गैसों के लिए निर्गम
- घोल के लिए निर्गम
- सीमेन्ट पाइप
बायोगैस संयंत्र में जीव द्रव्यमान प्रयोग किया जाता है। जीव द्रव्यमान के अतिरिक्त मानव मल का भी उपयोग किया जाता है। गोबर तथा जल के मिश्रण को संपाचक या मुख्य टैंक में एकत्रित किया जाता है। उत्पन्न गैस निर्गम द्वार से उपयोग के लिए उपलब्ध होती रहती है तथा गैस बन जाने के बाद यन्त्र में स्तरी बची रहती है, जिसमें अत्यधिक मात्रा में नाइट्रोजन तथा फॉस्फोरस यौगिक होते हैं। इसलिए इसका उपयोग एक अच्छी खाद के रूप में होता है।
प्रश्न 20.
वायु प्रवाह के लिये आवश्यक तीन कारक बतायें। समझाइए कि पवन ऊर्जा क्या है?
उत्तर:
पवन को गतिशील करने के लिए उत्तरदायी कारक – पवन के गतिशील होने के लिए निम्नलिखित तीन कारक उत्तरदायी हैं-
- सूर्य की स्थिति
- तापमान का अन्तर
- दाब का अन्तर
पवन ऊर्जा पृथ्वी का वायुमण्डल एक विशाल ऊष्मा इंजन की भाँति कार्य करता है। भूमध्य रेखीय क्षेत्रों मैं ध्रुवीय क्षेत्रों की अपेक्षा सौर प्रकाश की तीव्रता अधिक होती है। इसके परिणामस्वरूप भूमध्य रेखीय क्षेत्रों में पृथ्वी की सतह के निकट की वायु शीघ्र गर्म होकर ऊपर की ओर उठती है। इस खाली स्थान को भरने के लिये ध्रुवीय क्षेत्रों की अपेक्षाकृत ठण्डी वायु भूमध्य रेखीय क्षेत्रों की ओर बहने लगती है। इस बहती हुई वायु को पवन कहते हैं। वायु के विशाल द्रव्यमान की गतिशीलता से सम्बद्ध गतिज ऊर्जा ही पवन ऊर्जा है।
प्रश्न 21.
जैव गैस (बायोगैस) किसे कहते हैं? इसका संगठन लिखिए।
उत्तर:
जैव अपशिष्ट के विघटन से प्राप्त विभिन्न गैसों का मिश्रण जैव गैस या बायोगैस कहलाता है। इसका संगठन निम्न है – मिथेन (CH) गैस यह 65% होती है, इसके अतिरिक्त बायोगैस में कार्बन डाइ ऑक्साइड, हाइड्रोजन सल्फाइड आदि गैसें उत्पन्न होती हैं।
प्रश्न 22.
गोबर के सूखे कण्डों को जलाने से क्या हानियाँ होती हैं?
अथवा
गोवर के सूखे कण्डे बनाकर ईंधन के रूप में उपयोग करना अच्छी बात नहीं? इसके स्थान पर हमें क्या करना चाहिए और क्यों?
उत्तर:
गोबर के सूखे कण्डों को जलाने से हानियाँ – पशुओं के गोबर से बनाए गए सूखे कण्डों का दहन अपूर्ण होता है, जिसके फलस्वरूप वे अत्यधिक धुआँ उत्पन्न करते हैं। इससे वातावरण प्रदूषित होता है। पशुओं के गोबर में अनेक ऐसे महत्त्वपूर्ण पोषक तत्त्व हैं, जिन्हें मृदा में वापस पहुँचाने से मृदा की उपजाऊ शक्ति बनी रहती है। यदि गोबर के कण्डों को जलाया जाए, तो वे पोषक तत्त्व नष्ट हो जाते हैं। अतः गोबर कण्डों को सीधा जलाना विवेकपूर्ण नहीं है। गोबर को गोबर गैस में परिवर्तित करना चाहिए, जो कि एक साफ-सुथरा ईंधन है।
बहुविकल्पीय प्रश्न
1. सौर कुकर का वह भाग जो ग्रीन हाउस प्रभाव के लिए उत्तरदायी है-
(a) बॉक्स की काली परत
(b) दर्पण
(c) काँच की शीट
(d) कुकर का बाह्य आवरण
उत्तर:
(c) काँच की शीट
2. बायो गैस का मुख्य संघटक है-
(a) मेथेन
(b) CO2
(c) Ha
(d) SO2
उत्तर:
(a) मेथेन
3. ऊर्जा का अंतिम स्रोत कौन-सा है?
(a) जल
(b) सूर्य
(c) यूरेनियम
(d) जीवाश्मी ईंधन
उत्तर:
(b) सूर्य
4. नाभिकीय ऊर्जा के उपयोग में मुख्य समस्या क्या है?
(a) नाभिक का विखण्डन
(b) अभिक्रिया लगातार कैसे कराई जाए।
(c) उपयोग के बाद ईंधन का सुरक्षित निपटारा कैसे करें।
(d) नाभिकीय ऊर्जा का रूपान्तरण विद्युत ऊर्जा में कैसे करें।
उत्तर:
(c) उपयोग के बाद ईंधन का सुरक्षित निपटारा कैसे करें।
5. नाभिकीय बम को अधिविस्फोटित करने पर ताप (कुछ ही माइक्रोसेकण्ड में) हो जाता है-
(a) 107K
(b) 109K
(c) 109K
(d) 106K
उत्तर:
(a) 107K
6. पवनों का देश किसे कहा जाता है?
(a) स्वीडन
(b) डेनमार्क
(c) भारतवर्ष
(d) अमेरिका।
उत्तर:
(b) डेनमार्क

7. ऊर्जा के निम्नलिखित रूपों में से किसकी साज-सज्जा और उपयोग की प्रक्रिया में सबसे कम पर्यावरणीय प्रदूषण होता है?
(a) नाभिकीय ऊर्जा
(b) तापीय ऊर्जा
(c) सौर ऊर्जा
(d) भूतापीय ऊर्जा
उत्तर:
(c) सौर ऊर्जा
8. महासागरीय तापीय ऊर्जा का कारण है-
(a) महासागर तरंगों द्वारा संचित ऊर्जा
(b) महासागर में विभिन्न स्तरों पर ताप में अंतर
(c) महासागर में विभिन्न स्तरों पर दाब में अंतर
(d) महासागर में उत्पन्न ज्वार
उत्तर:
(b) महासागर में विभिन्न स्तरों पर ताप में अंतर
9. पवन चक्की में उत्पन्न ऊर्जा-
(a) वर्षा ऋतु में अधिक होती है क्योंकि नम वायु होने पर पंखुड़ियों से वायु का अधिक द्रव्यमान टकराता है।
(b) मीनार (टावर) की ऊँचाई : निर्भर करती है।
(c) पवन के वेग पर निर्भर करती है।
(d) मीनार के निकट ऊँचे वृक्ष लगाकर बढ़ाई जा सकती है।
उत्तर:
(c) पवन के वेग पर निर्भर करती है।
10. 1MW के जनित्र के लिए पवन फार्म को कितनी भूमि चाहिए?
(a) 3 हेक्टेयर
(b) 2 हेक्टेयर
(c) 4 हेक्टेयर
(d) 5 हेक्टेयर
उत्तर:
(b) 2 हेक्टेयर
11. प्रारूपी सौर सेल से कितनी विद्युत उत्पन्न होती है?
(a) 0.8 W
(b) 0.7 W
(c) 10W
(d) 11W
उत्तर:
(b) 0.7 W
12. जल विद्युत संयंत्र में-
(a) संचित जल की स्थितिज ऊर्जा विद्युत में रूपांतरित हो जाती है।
(b) संचित जल की गतिज ऊर्जा स्थितिज ऊर्जा में रूपांतरित हो जाती है।
(c) जल से विद्युत निष्कर्ष की जाती है।
(d) विद्युत प्राप्त करने के लिए जल को भाप में रूपांतरित किया जाता है।
उत्तर:
(a) संचित जल की स्थितिज ऊर्जा विद्युत में रूपांतरित हो जाती है।
13. महासागरों से हम कौन-सा ऊर्जा का स्रोत प्राप्त कर सकते हैं?
(a) ज्वारीय ऊर्जा
(b) तरंग ऊर्जा
(c) महासागर तापीय ऊर्जा
(d) ये सभी।
उत्तर:
(d) ये सभी।
14. प्राकृतिक रूप में ठोस ईंधन कौन-सा है?
(a) कोक
(b) कोयला
(c) CNG
(d) LPG
उत्तर:
(b) कोयला
15. सौर कुकर के पृष्ठ भाग को कौन से रंग से पोता जाता है ताकि वह अधिक से अधिक ऊष्मा को अवशोषित कर सकें?
(a) सफेद
(b) पीला
(c) लाल
(d) काला।
उत्तर:
(d) काला।
16. आधुनिक सौर सेल की कार्य करने की योग्यता आपके विचार से कितनी है?
(a) 75%
(b) 50%
(c) 25%
(d) 100%
उत्तर:
(c) 25%
17. भारत में भूतापीय ऊर्जा से विद्युत कहाँ उत्पन्न की जाती है?
(a) मध्यप्रदेश
(b) गुजरात
(c) हरियाणा
(d) महाराष्ट्र।
उत्तर:
(a) मध्यप्रदेश
18. सौर ऊर्जा का रासायनिक ऊर्जा में रूपान्तरण को क्या कहते हैं?
(a) प्रकाश संश्लेषण
(b) श्वसन
(c) पाचन
(d) ये सभी
उत्तर:
(a) प्रकाश संश्लेषण
19. हाइड्रोजन बम में कौन-सी अभिक्रिया प्रयुक्त होती है?
(a) नाभिकीय अभिक्रियाएँ
(b) रासायनिक अभिक्रियाएँ
(c) थर्मो नाभिकीय अभिक्रियाएँ
(d) इनमें से कोई नहीं।
उत्तर:
(c) थर्मो नाभिकीय अभिक्रियाएँ
रिक्त स्थानों की पूर्ति कीजिए
- प्राचीन काल में ऊष्मीय ऊर्जा का सामान्य स्रोत ………………… था।
- ………………… ईंधन ऊर्जा के अनवीकरणीय स्रोत हैं।
- भारत का पवन ऊर्जा द्वारा विद्युत उत्पादन करने वाले देशों में ………………… स्थान है।
- धूप में रखने पर किसी सौर सेल में ………………… तक वोल्टता विकसित होती है।
- हाइड्रोजन बम ………………… पर आधारित होता है।
उत्तर:
- लकड़ी
- जीवाश्मी
- पाँचवाँ
- 0.5-1.0V
- नाभिकीय संलयन।
![]()

![]()

![]()


![]()

![]()












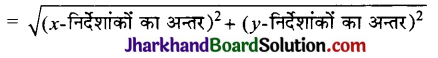



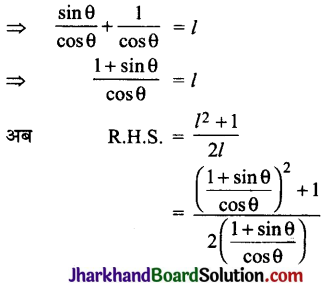
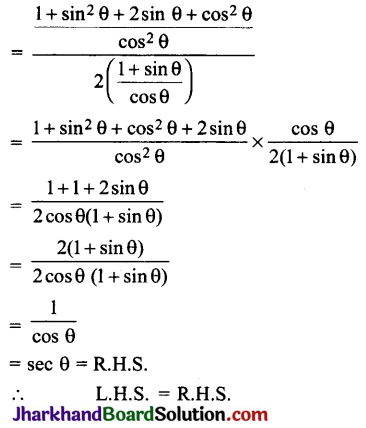
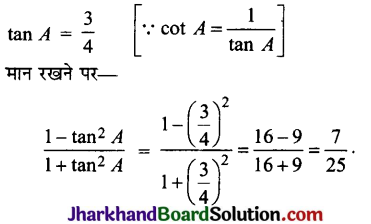
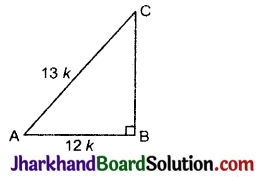

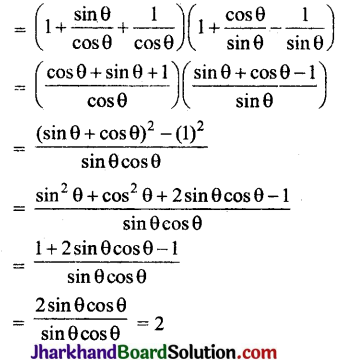

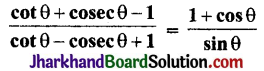



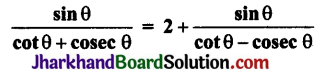
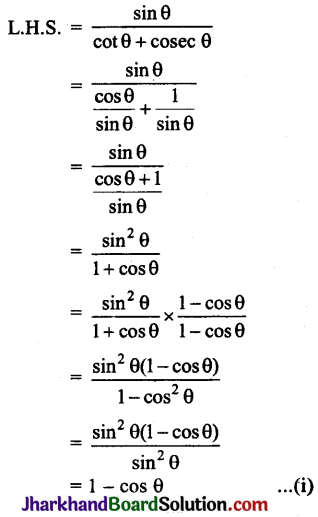
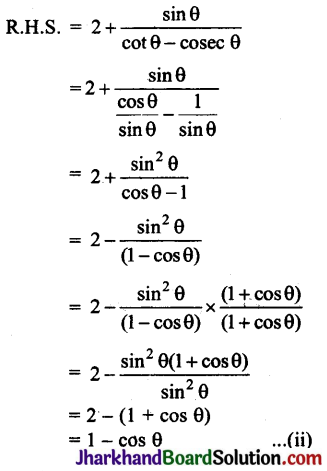
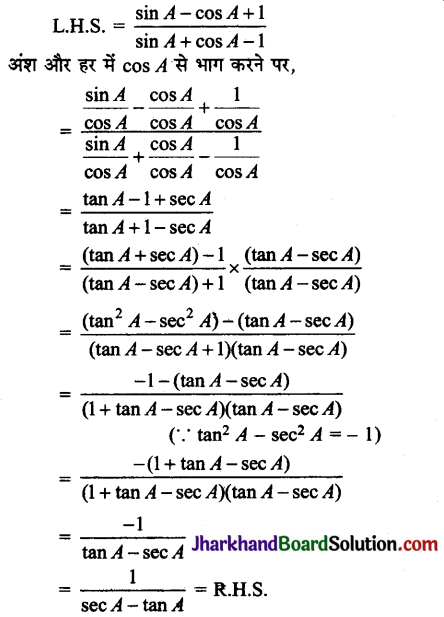
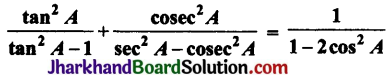
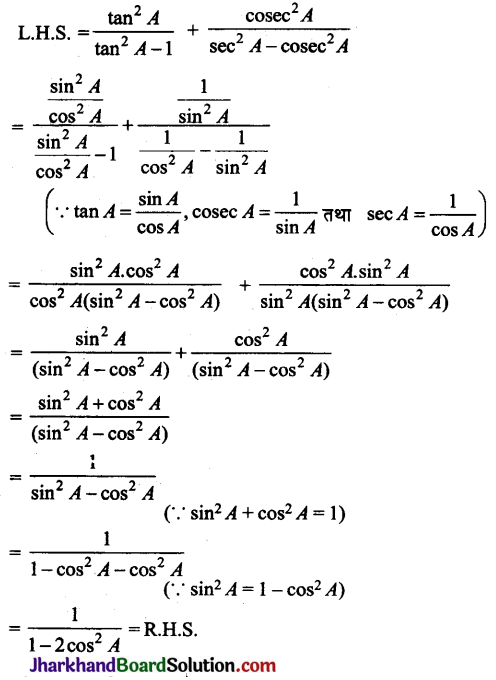




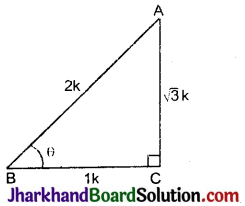
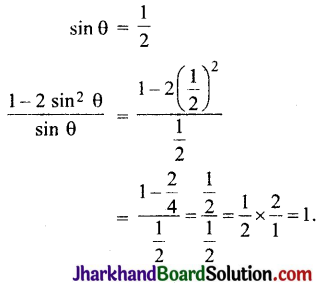
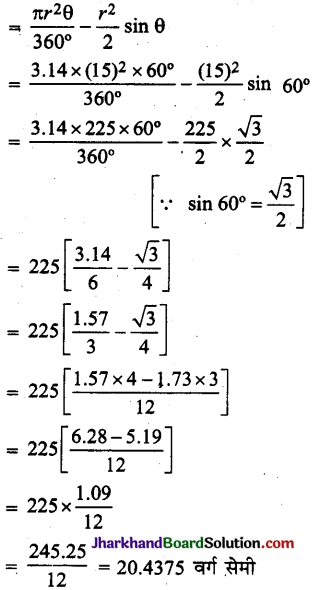
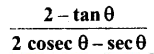 बराबर है:
बराबर है: