Jharkhand Board JAC Class 9 Science Solutions Chapter 8 गति Textbook Exercise Questions and Answers.
JAC Class 9 Science Solutions Chapter 8 गति
Jharkhand Board Class 9 Science गति Textbook Questions and Answers
प्रश्न 1.
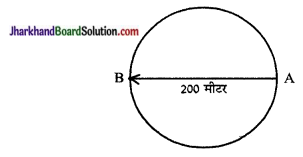
एक एथलीट वृत्तीय रास्ते, जिसका व्यास 200 मीटर है, का एक चक्कर 40 सेकण्ड में लगाता है। 2 मिनट 20 सेकण्ड के बाद वह कितनी दूरी तय करेगा और उसका विस्थापन क्या होगा?
हल:
∵ व्यास 2 = 200 मीटर
∴ एक चक्कर में तय किए गए पथ की लम्बाई = परिधि = 2πr = π (2r) = \(\frac { 22 }{ 7 }\) x 200 मीटर
∵ एक चक्कर लगाने का समय = 40 सेकण्ड
2 मिनट 20 सेकण्ड (= 140 सेकण्ड) में चक्करों की संख्या = \(\frac { 140 }{ 40 }\) = 3.5 चक्कर
∴ कुल तय दूरी = 3.5 चक्करों में तय दूरी
= 3.5 x एक चक्कर तय दूरी
= 3.5 x \(\frac { 22 }{ 7 }\) x 200 = 2,200 मीटर।
3-5 चक्करों के बाद एथलीट अपने प्रारम्भिक बिन्दु ‘A’ से जाने वाले व्यास के विपरीत सिरे ‘B’ पर होगा।
∴ एथलीट का विस्थापन व्यास AB की लम्बाई
= 200 मीटर।
![]()
प्रश्न 2.
300 मीटर के सीधे रास्ते पर जोसेफ जॉगिंग करता हुआ 2 मिनट 50 सेकण्ड में एक सिरे ‘A’ से दूसरे सिरे ‘B’ पर पहुँचता है और घूमकर 1 मिनट में 100 मीटर पीछे बिन्दु ‘C’ पर पहुँचता है। जोसेफ की औसत चाल और औसत वेग क्या होंगे?
(a) सिरे ‘A’ से दूसरे सिरे ‘B’ तक तथा
(b) सिरे ‘A’ से सिरे ‘C’ तक।
हल:
(a) सिरे ‘A’ से सिरे ‘B’ तक-
कुल तय दूरी AB = 300 मीटर
तथा लिया गया समय t = 2 मिनट 50 सेकण्ड
= 2 × 60 + 50 सेकण्ड
= 170
सेकण्ड
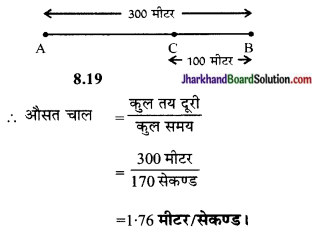
पुनः विस्थापन प्रारम्भिक बिन्दु ‘A’ से अन्तिम बिन्दु ‘B’ तक सरल रेखीय दूरी
= AB = 300 मीटर
तथा लगा समय t = 170 सेकण्ड
∴ औसत वेग

= 1.76 मीटर/सेकण्ड A से B की ओर।
(b) सिरे ‘A’ से सिरे ‘C’तक-
कुल तय दूरी = AB + BC = 300 + 100
= 400 मीटर
तथा कुल समय = 2 मिनट 50 सेकण्ड + 1 मिनट
= 170 सेकण्ड + 60 सेकण्ड
= 230 सेकण्ड।

पुनः विस्थापन = प्रारम्भिक बिन्दु ‘A’ से अन्तिम बिन्दु ‘C’ तक सरल रेखीय दूरी
= AC = AB – BC
= 300 – 100
= 200 मीटर
जबकि कुल समय = 230 सेकण्ड

= 0.87 मीटर/सेकण्ड A से C की ओर।
प्रश्न 3.
अब्दुल गाड़ी से स्कूल जाने के क्रम में औसत चाल को 20 किमी/ घण्टा पाता है। उसी रास्ते से लौटने के समय वहाँ भीड़ कम है और औसत चाल 40 किमी / घण्टा है। अब्दुल की इस पूरी यात्रा में उसकी औसत चाल क्या है?
हल:
माना कि घर से स्कूल तक यात्रा-मार्ग की म्बाई = किमी
जाते समय औसत चाल = 20 किमी/घण्टा

इसी प्रकार,
∵ लौटते समय औसत चाल = 40 किमी/घण्टा
लौटने में लगा समय t2 है तब
लौटने में लगा समय t2 =

∴ स्कूल जाने और लौटने में लगा कुल समय
t = t1 + t2 = \(\frac { s }{ 20 }\) + \(\frac { s }{ 40 }\)
= \(\frac { 2s+s }{ 40 }\)
= \(\frac { 3s }{ 40 }\)
जबकि तय की गई कुल दूरी = s + s = 2 s

प्रश्न 4.
कोई मोटरबोट झील में विरामावस्था से सरल रेखीय पथ पर 3-0 मीटर/सेकण्ड के नियत त्वरण से 8-0 सेकण्ड तक चलती है। इस समयान्तराल में मोटरबोट कितनी दूरी तय करती है?
हल:
दिया है प्रारम्भिक वेग u = 0, त्वरण a = 3.0 मीटर / सेकण्ड²,
समय t = 8.0 सेकण्ड तथा तय दूरी s = ?
सूत्र s = ut + at² से, s = 0 x 8 + \(\frac { 1 }{ 2 }\) × 3.0 × (8.0)²
= \(\frac { 1 }{ 2 }\) × 3 × 64
= 96 मीटर
∴ मोटरबोट द्वारा 8-0 सेकण्ड में तय दूरी 96 मीटर।
प्रश्न 5.
किसी गाड़ी का चालक 52 किमी / घण्टा की गति से चल रही कार में ब्रेक लगाता है तथा कार विपरीत दिशा में एकसमान दर से त्वरित होती है। कार 5 सेकण्ड में रुक जाती है। दूसरा चालक 30 किमी/ घण्टा की गति से चल रही दूसरी कार पर धीमे-धीमे ब्रेक लगाता है तथा 10 सेकण्ड में रुक जाता है। एक ही ग्राफ पेपर पर दोनों कारों के लिए चाल – समय ग्राफ आलेखित कीजिए। ब्रेक लगाने के पश्चात् दोनों में से कौन-सी कार अधिक दूरी तक जाएगी?
हल:
पैमाना Y-अक्ष : 1 सेमी = 10 किमी / घण्टा
X-अक्ष: 1 सेमी = 1 सेकण्ड
दोनों कारों के चाल- समय ग्राफ चित्र 8.20 में प्रदर्शित है।
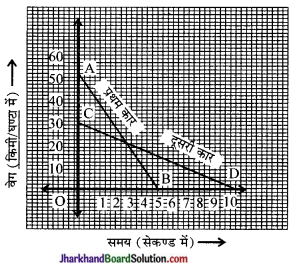
ब्रेक लगाने के बाद रुकने तक कारों द्वारा तय दूरियाँ ज्ञात करना-
प्रथम कार द्वारा तय दूरी ग्राफ AB के नीचे घिरा क्षेत्रफल
= ∆AOB का क्षेत्रफल = \(\frac { 1 }{ 2 }\) OA x OB
= \(\frac { 1 }{ 2 }\) x (52 किमी / घण्टा ) x 5 सेकण्ड
= \(\frac { 1 }{ 2 }\) [52 x \(\frac { 5 }{ 18 }\) मीटर/सेकण्ड] x 5 सेकण्ड
= 36.11 मीटर
दूसरी कार द्वारा तय दूरी ∆COD का क्षेत्रफल
= \(\frac { 1 }{ 2 }\) OC X OD
= \(\frac { 1 }{ 2 }\) x (30 किमी / घण्टा) x 10 सेकण्ड
= \(\frac { 1 }{ 2 }\) [30 × 18 मीटर/सेकण्ड] x 10 सेकण्ड
= 41.67 मीटर
स्पष्ट है कि रुकने से पूर्व दूसरी कार अधिक दूरी तक जाएगी।
प्रश्न 6.
संलग्न चित्र में तीन वस्तुओं A, B तथा C के दूरी- समय ग्राफ प्रदर्शित हैं। ग्राफ का अध्ययन करके निम्नलिखित प्रश्नों के उत्तर दीजिए-
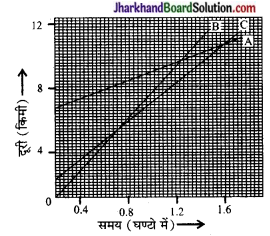
(a) तीनों में से कौन सबसे तीव्र गति से गतिमान है?
(b) क्या ये तीनों किसी भी समय सड़क के एक ही बिन्दु पर होंगे?
(c) जिस समय B, A से गुजरती है उस समय तक C कितनी दूरी तय कर लेती है?
(d) जिस समय B, C से गुजरती है, उस समय तक यह कितनी दूरी तय कर लेती है?
उत्तर:
(a) हम जानते हैं कि दूरी समय ग्राफ का ढाल, वस्तु की चाल को प्रदर्शित करता है।
∵ ग्राफ B का ढाल सर्वाधिक है, इसका अर्थ यह है कि वस्तु B सबसे तीव्र गति से गतिमान है।
(b) चूँकि तीनों ग्राफ परस्पर एक ही बिन्दु पर नहीं काटते हैं, अर्थात् तीनों वस्तुएँ किसी भी समय सड़क के एक ही बिन्दु पर नहीं होंगी।
(c) जिस समय B, A से गुजरती है, उस समय C की मूल बिन्दु की दूरी 8 किमी (ग्राफ से पढ़ने पर)
(d) जिस समय B,C से गुजरती है, उस समय तक B तथा C दोनों की मूल बिन्दु से दूरियाँ 5.1 किमी (ग्राफ से पढ़ने पर)।
![]()
प्रश्न 7.
20 मीटर की ऊँचाई से एक गेंद को गिराया जाता है। उसका वेग 10 मीटर / सेकण्ड के एक समान त्वरण की दर से बढ़ता है तो यह किस वेग से धरातल से टकराएगी? कितने समय पश्चात् वह धरातल से टकराएगी?
हल:
दिया है: 0, h = 20 मीटर, 8 10 मीटर / सेकण्ड 2, v = ?, t = ?
सूत्र
v² – u² = 2 as से,
v² – 0² = 2 × 10 × 20 या
v² = 20 x 20 = 400
∴ v = \(\sqrt{400}\)
= 20 मीटर / सेकण्ड
पुन: सूत्र
v = u + gt से,
20 = 0 + 10 × t
⇒ t = \(\frac { 20 }{ 10 }\) = 2 सेकण्ड
अतः गेंद धरातल से 2 सेकण्ड बाद, 20 मीटर / सेकण्ड के वेग से टकराएगी।
प्रश्न 8.
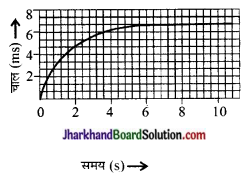
किसी कार का चाल-समय ग्राफ संलग्न चित्र 8.22 में प्रदर्शित किया गया है-
(a) पहले 4 सेकण्ड में कार कितनी दूरी तय करती है? इस अवधि में कार द्वारा तय दूरी को ग्राफ में छायांकित क्षेत्र द्वारा दर्शाइए।
(b) ग्राफ का कौन-सा भाग कार की एकसमान को दर्शाता है?
उत्तर:
(a) प्रथम 4 सेकण्ड में कार द्वारा तय दूरी को निम्न चित्र में छायांकित क्षेत्र द्वारा प्रदर्शित किया गया है।
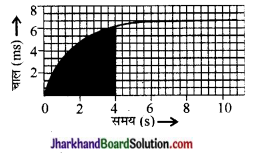
(b) प्रथम 6 सेकण्ड के बाद का ग्राफ एक क्षैतिज रेखा है, अर्थात् ग्राफ काढाल (त्वरण) शून्य है; अतः ग्राफ का यह भाग कार की एकसमान गति को प्रदर्शित करता है।
प्रश्न 9.
निम्नलिखित में कौन-सी अवस्थाएँ सम्भव हैं तथा प्रत्येक के लिए एक उदाहरण दीजिए – (a) कोई वस्तु जिसका त्वरण नियत हो परन्तु वेग शून्य हो। (b) कोई त्वरित वस्तु एकसमान चाल से गति कर रही हो। (c) कोई वस्तु किसी निश्चित दिशा में गति कर रही हो तथा त्वरण उसके लम्बवत् हो।
उत्तर:
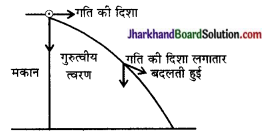
(a) सम्भव है। मकान की छत से छोड़ते समय गेंद का वेग शून्य होता है, जबकि त्वरण नियत रहता है।
(b) सम्भव है। वृत्तीय गति में एकसमान चाल हो सकती है।
(c) असम्भव है; क्योंकि यदि त्वरण गति की दिशा के लम्बवत् दिशा में है तो दिशा निश्चित नहीं रह सकती, वह समय के साथ बदल जाएगी।
उदाहरण- जब किसी मकान की छत से किसी गेंद को क्षैजित दिशा में फेंका जाता है तो गेंद पर गुरुत्वीय त्वरण गति की दिशा के लम्ब दिशा में कार्य करता है जिस कारण उसकी गति की दिशा बदलती जाती है।
प्रश्न 10.
एक कृत्रिम उपग्रह 42, 250 किमी त्रिज्या की वृत्ताकार कक्षा में घूम रहा है। यदि वह 24 घण्टे में में पृथ्वी की परिक्रमा करता है तो उसकी चाल का परिकलन कीजिए।
हल:
दिया है : कक्षा की त्रिज्या r = 42, 250 किमी
एक चक्कर लगाने का समय (परिक्रमण काल)
घण्टे = 24 x 60 x 60 सेकण्ड
∴ एक चक्कर में तय दूरी = परिधि = 2πr

Jharkhand Board Class 9 Science गति InText Questions and Answers
क्रियाकलाप 8.1. (पा. पु. पृ. सं. 108)
आपकी कक्षा की दीवार विरामावस्था में है या गति में, चर्चा करें।
उत्तर:
कक्षा की दीवार विरामावस्था में है।
क्रियाकलाप 8.2.
क्या आपने कभी अनुभव किया है कि रेलगाड़ी, जिसमें आप बैठे हैं, गति करती हुयी प्रतीत होती है जबकि वास्तव में वह विरामावस्था में है?
उत्तर:
जब हम किसी रुकी हुयी रेलगाड़ी में बैटे हों तथा उसके सापेक्ष दूसरी रेलगाड़ी गति करती हो। तब ऐसा प्रतीत होता है कि हम जिस रेलगाड़ी में बैठे हैं वह गति कर रही है।
क्रियाकलाप 8.3. (पा. पु. पृ. सं. 110)
एक मीटर स्केल एवं एक लम्बी रस्सी लेकर बास्केटबॉल कोर्ट के एक कोने से दूसरे कोने तक उसके किनारे से होते हुए जाए तथा अपने द्वारा तय की गई दूरी तथा विस्थापन के परिमाण को मापें। दोनों स्थितियों में प्रेक्षित अन्तर को वर्णित करें।
क्रियाकलाप 8.4.
गाड़ियों में तय की गई दूरी को प्रदर्शित करने के लिए एक यन्त्र लगा होता है, उसे ओडोमीटर कहा जाता है। भुवनेश्वर से नई दिल्ली जाते समय ओडोमीटर के अन्तिम पाठ्यांक और आरम्भिक पाठ्यांक का अन्तर 1850 किमी है। मानचित्र की सहायता से भुवनेश्वर तथा नई दिल्ली के बीच के विस्थापन (न्यूनतम दूरी) के परिमाण को ज्ञात करें।
खंड 8.1 से सम्बन्धित पाठ्य-पुस्तक के प्रश्नोत्तर (पा. पु. पृ. सं. 110)
प्रश्न 1.
एक वस्तु के द्वारा कुछ दूरी तय की गई। क्या इसका विस्थापन शून्य हो सकता है? अगर हाँ, तो अपने उत्तर को उदाहरण के द्वारा समझाइए।
उत्तर:
हाँ, वस्तु का विस्थापन शून्य हो सकता है। उदाहरणार्थं – यदि एक छात्र सुबह अपने घर से स्कूल को जाता है जो घर से 4 किमी की दूरी पर है तथा दोपहर बाद घर वापस लौटता है तो उसके द्वारा तय की गई दूरी तो 8 किमी होगी, जबकि उसका विस्थापन शून्य होगा (∵ प्रारम्भिक तथा अन्तिम बिन्दु एक ही हैं।)
![]()
प्रश्न 2.
एक किसान 10 मीटर भुजा वाले एक वर्गाकार खेत की सीमा पर 40 सेकण्ड में चक्कर लगाता है। 2 मिनट 20 सेकण्ड के बाद किसान के विस्थापन का परिमाण क्या होगा?
हल:
दिया है: एक चक्कर का समय 40 सेकण्ड
जबकि कुल समय = 2 मिनट, 20 सेकण्ड
= (2 x 60 + 20) सेकण्ड
= 120 + 20 = 140 सेकण्ड
140 सेकण्ड में किसान 3 चक्कर पूर्ण करने के बाद, अपने प्रारम्भिक बिन्दु से विकर्णत: विपरीत कोने पर होगा।
अतः किसान के विस्थापन का परिमाण = विकर्ण AC की लम्बाई
∆ ABC में,
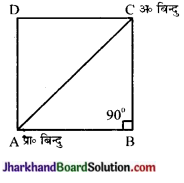
AB = 10 मीटर,
BC = 10 मीटर
जबकि ∠ABC = 90°
∴ पाइथागोरस प्रमेय से,
AC² = AB² + BC²
= (10)² + (10)²
= 100 + 100 – 200
= 100 × 2
वर्गमूल लेने पर, AC = 10\(\sqrt{2}\) मीटर
= 10 × 1.414 = 14.14 मीटर
अत: किसान के विस्थापन का परिणाम 10\(\sqrt{2}\) मीटर या 14-14 मीटर है।
प्रश्न 3.
विस्थापन के लिए निम्नलिखित में कौन सही है?
(a) यह शून्य नहीं हो सकता है।
(b) इसका परिमाण वस्तु के द्वारा तय की गई दूरी से अधिक होता है।
उत्तर:
विस्थापन के लिए उपर्युक्त दोनों में से कोई भी कथन सत्य नहीं हैं।
क्रियाकलाप 8.5. (पा.पु. पू. सं. 110)
दो वस्तुओं A व B की गति से सम्बन्धित आँकड़ों को सारणी 81 में दिया गया है। इसमें बताएँ कि वस्तुओं की गति एक समान है या असमान।
सारणी 8.1
| समय | वस्तु A के द्वारा तय की गई दूरी मीटर में | वस्तु B के द्वारा तय की गई दूरी मीटर में |
| 9.30 am | 10 | 12 |
| 9.45 am | 20 | 19 |
| 10.00 am | 30 | 23 |
| 10.15 am | 40 | 35 |
| 10.35 am | 50 | 37 |
| 10.45 am | 60 | 41 |
| 11.00 am | 70 | 44 |
प्रश्न 1.
उपरोक्त सारणी से बताएँ कि वस्तु A द्वारा तय की गई गति असमान है या एकसमान।
उत्तर:
एकसमान।
प्रश्न 2.
वस्तु B द्वारा तय की गई गति एकसमान है या असमान।
उत्तर:
असमान।
प्रश्न 3.
एकसमान गति किसे कहते हैं?
उत्तर:
किसी वस्तु द्वारा समान समयांतराल में समान दूरी तय करना एकसमान गति कहलाता है।
प्रश्न 4.
असमान गति किसे कहते हैं?
उत्तर:
किसी वस्तु द्वारा समान समयांतराल में तय की गई असमान दूरी को असमान गति कहते हैं।
क्रियाकलाप 8.6. (पा.पु. पृ. सं. 112)
अपने घर से जाने में लगे समय को मापिए। यदि आपके पैदल चलने की औसत चाल 4 किमी / घण्टा है तो अपने घर से स्कूल की दूरी की आकलन करें।
क्रियाकलाप 8.7 (पा.पु. पृ. सं. 112)
आसमान में बादल छाए होने पर बिजली के चमकने और बादलों के गरजने की क्रिया बार-बार होती है। पहले बिजली की चमक दिखाई देती है तथा कुछ समय पश्चात् बादलों के गरजने की ध्वनि हमारे कानों तक पहुँचती है।
इनके बीच के समायन्तराल को एक डिजिटल स्टॉप घड़ी से मापें।
प्रश्न 1.
बिजली की चमक पहले तथा ध्वनि बाद में सुनाई क्यों देती है?
उत्तर:
प्रकाश की चाल (3 x 108 m/s), ध्वनि की चाल (346m/s) से बहुत अधिक होती है। इस कारण से बिजली की चमक पहले तथा ध्वनि बाद में सुनाई देती है।.
खण्ड 8.2 से सम्बन्धित पाठ्य-पुस्तक के प्रश्नोत्तर। (पा.पु. पृ. सं. 112)
प्रश्न 1.
चाल एवं वेग में अन्तर बताइए।
उत्तर:
चाल तथा वेग में अन्तर
| चाल | देग |
| 1. किसी वस्तु द्वारा, दूरी तय करने की समय दर को उसकी चाल कहते हैं। | 1. किसी वस्तु द्वारा, विस्थापन तय करने की समय दर को उसका वेग कहते हैं। |
| 2. यह अदिश राशि होती है, जिसमें केवल परिमाण होता है। | 2. यह एक सदिश राशि होती है जिसमें परिमाण के साथ दिशा भी होती है। |
| 3. यह सदैव धनात्मक होती है। | 3. यह धनात्मक तथा ऋणात्मक दोनों हो सकता है। |
प्रश्न 2.
किस अवस्था में किसी वस्तु के औसत वेग का परिमाण उसकी औसत चाल के बराबर होता है?
उत्तर:
यदि वस्तु एक सरल रेखा में गति कर रही है तो उसके औसत वेग का परिमाण, उसकी औसत चाल के बराबर होगा।
प्रश्न 3.
एक गाड़ी का ओडोमीटर क्या मापता है?
उत्तर:
गाड़ी का ओडोमीटर, उसके द्वारा तय की गई दूरी को मापता है।
प्रश्न 4.
जब वस्तु एकसमान गति में होती है तो उसका मार्ग कैसा दिखाई पड़ता है?
उत्तर:
जब वस्तु एकसमान गति में होती है, तब उसका मार्ग एक सरल रेखा जैसा दिखाई पड़ता है।
प्रश्न 5.
एक प्रयोग के दौरान, अन्तरिक्ष यान से एक सिग्नल को पृथ्वी पर पहुँचने में 5 मिनट का समय लगता है। पृथ्वी पर स्थित स्टेशन से उस अन्तरिक्ष यान की दूरी क्या है?
दिया है, सिग्नल की चाल-प्रकाश की चाल
= 3 x 108 मीटर/सेकण्ड।
हल:
दिया है : सिग्नल द्वारा पृथ्वी तक पहुँचने में लगा समय
t = 5 मिनट 300 सेकण्ड
∴ स्टेशन से अन्तरिक्ष यान की दूरी = सिग्नल की चाल x लगा समय
= 3 x 108 (मीटर / सेकण्ड ) x 300 सेकण्ड
= 9 × 1010 मीटर
= \(\frac{9 \times 10^{10}}{1000}\) किमी।
= 9 × 107 किमी।
![]()
उदाहरण 8.2.
यात्रा शुरू होते समय कार का ओडोमीटर 2000 km प्रदर्शित करता है और यात्रा समाप्ति पर 2400 km प्रदर्शित करता है। यदि इस यात्रा में 8h लगते हैं, तो कार की औसत चाल को km h-1 और ms-1 में ज्ञात करें।
हल:
कार के द्वारा तय की गई दूरी
s = 2400 km – 2000 km = 400 km
दूरी तय करने में लगा कुल समय
‘t’ = 8 h.
कार की औसत चाल
vav = \(\frac { s }{ t }\)
= \(\frac { 400 km}{ 8h }\)
= 50 km h-1
= 50 \(\frac{\mathrm{km}}{\mathrm{h}} \times \frac{1000 \mathrm{~m}}{1 \mathrm{~km}} \times \frac{1 \mathrm{~h}}{3600 \mathrm{~s}}\)
= 13.9ms-1
कार की औसत चाल 50kmh1 अथवा 13.9ms 1 है।
उदाहरण 8.3.
ऊषा 90 लम्बे तालाब में तैरती है। वह एक सिरे से दूसरे सिरे तक सरल रेखीय पथ पर जाती है तथा वापस आती है। इस दौरान वह कुल 180 mm की दूरी 1 मिनट में तय करती है। ऊषा की औसत चाल और औसत वेग को ज्ञात कीजिए।
हल:
ऊषा द्वारा 1 मिनट में तय की गई कुल दूरी 180 m है।
1 मिनट में ऊषा का विस्थापन = 0 m
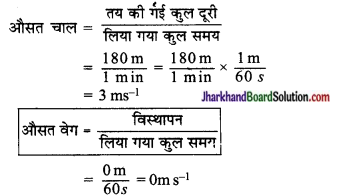
अतः ऊषा की औसत चाल 3 ms-1 है और औसत वेग 0ms-1 है।
क्रियाकलाप 8.8. (पा.पु. पू. सं. 114)
आप दैनिक जीवन में बहुत प्रकार की गतियों को देखते होंगे, जिनमें प्रमुख हैं: (a) त्वरण गति की दिशा में हो (b) त्वरण गति की दिशा के विपरीत है। (c) एक समान त्वरण है, तथा (d) असमान त्वरण है।
क्या ऊपर दिए गए प्रत्येक प्रकार की गति के लिए एक-एक उदाहरण दे सकते हैं।
उदाहरण 8.4.
राहुल अपनी साइकिल को विरामावस्था से चलाना शुरू करता है और 30s में 6ms का वेग प्राप्त करता है। वह इस इस प्रकार से ब्रेक लगाता है कि साइकिल का वेग अगले 5s में कम होकर 4 ms-1 हो जाता है। दोनों स्थितियों में साइकिल के त्वरण का परिकलन करें।
हल:
पहली स्थिति में
प्रारम्भिक वेग u = 0; अन्तिम वेग = 6m/s
समय t = 30s.
समीकरण से,
त्वरण a = \(\frac { v-u }{ t }\)
u, v और t का दिया हुआ मान समीकरण में रखने पर,
a = \(\frac{\left(6 m s^{-1}-0 m s^{-1}\right)}{30 s}\) = 0.2 ms-2
दूसरी स्थिति में,
प्रारम्भिक वेग u = 6 ms-1
अन्तिम वेग v = 4 ms-1; तथा समय t = 5s.
तब, a = \(\frac{\left(4 m s^{-1}-6 m s^{-1}\right)}{5 s}\) = – 0.4 ms-2
साइकिल का त्वरण पहली स्थिति में 0.2 ms-2 है और दूसरी स्थिति में – 0.04ms-2 है।
खण्ड 8.3 से सम्बन्धित पाठ्य पुस्तक के प्रश्नोत्तर (पा.पु. पृ. सं. 114 )
प्रश्न 1.
आप किसी वस्तु के बारे में कब कहेंगे कि, (i) वह एकसमान त्वरण से गति में है? (ii) वह असमान त्वरण से गति में है?
उत्तर:
- जब वस्तु एक सरल रेखा में गतिमान हो तथा समान समयान्तरालों में इसका वेग समान रूप से घटता या बढ़ता हो।
- जब समान समयान्तरालों में वस्तु का वेग असमान रूप से परिवर्तित होता हो।
प्रश्न 2.
एक बस की गति 5 सेकण्ड में 80 किमी/घण्टा से घटकर 60 किमी/घण्टा हो जाती है। बस का त्वरण ज्ञात कीजिए।
हल:
बस का प्रारम्भिक वेग 480 किमी/घण्टा
= 80 × \(\frac { 5 }{ 18 }\) मीटर / सेकण्ड
= \(\frac { 200 }{ 9 }\) मीटर/सेकण्ड
जबकि अन्तिम वेग v = 60 किमी / घण्टा
= 60 × \(\frac { 5 }{ 18 }\) मीटर / सेकण्ड
= \(\frac { 50 }{ 3 }\) मीटर/सेकण्ड
समयान्तराल t = 5 सेकण्ड
∴ बस का त्वरण a = \(\frac{v-u}{t}=\frac{\frac{50}{3}-\frac{200}{9}}{5}\)
= \(\frac{(150-200) / 9}{5}=\frac{-50}{5 \times 9}=-\frac{10}{9}\)
अत: बस का त्वरण a = 10/9 मीटर / सेकण्ड।
प्रश्न 3.
एक रेलगाड़ी स्टेशन से चलना प्रारम्भ करती है और एकसमान त्वरण के साथ चलते हुए 10 मिनट में 40 किमी / घण्टा की चाल प्राप्त करती है। इसका त्वरण ज्ञात कीजिए।
हल:
स्टेशन पर रेलगाड़ी का प्रारम्भिक वेग 14 = 0
जबकि अन्तिम वेग v = 40 किमी / घण्टा
= 40 x \(\frac { 5 }{ 18 }\) = \(\frac { 100 }{ 9 }\) मीटर / सेकण्ड
लिया गया समय t = 10 मिनट
= 10 × 60 = 600 सेकण्ड
∴ रेलगाड़ी का त्वरण
a = \(\frac{v-u}{t}=\frac{\frac{100}{9}-0}{600}=\frac{100}{9 \times 600}=\frac{1}{54}\)
= 0.018 मीटर/सेकण्ड²।
क्रियाकलाप 8.9. (पा. पु. पृ. सं. 117)
एक ट्रेन के तीन विभिन्न स्टेशनों A, B और C पर आगमन और प्रस्थान करने के समय एवं स्टेशन A से स्टेशन B व C की दूरी निम्न सारणी 8.2 में दी गई है। मान लें कि किन्हीं दो स्टेशनों के बीच ट्रेन की गति एकसमान है तो इस आधार पर वेग-समय ग्राफ खींचें तथा व्याख्या करें।
सारणी 8.2 : स्टेशन A से B तथा C की दूरी तथा ट्रेन के आगमन व प्रस्थान करने का समय
| स्टेशन | A से दूरी (Km) | आगमन का समय (घण्टे) | प्रस्थान का समय (घण्टे) |
| A | 0 | 08 : 00 | 08 : 15 |
| B | 120 | 11 : 15 | 11 : 30 |
| C | 180 | 13 : 00 | 13 : 15 |
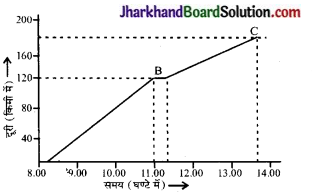
क्रियाकलाप 8.10.
फिरोज और उसकी बहन सानिया अपनी साइकिलों से स्कूल जाते हैं। वे दोनों घर से एक ही समय पर प्रस्थान करते हैं एवं एक ही मार्ग से जाते हैं फिर भी अलग-अलग समय पर स्कूल पहुँचते हैं। सारणी 8.13 उन दोनों के द्वारा अलग-अलग समय में तय की गई दूरी को दर्शाती है। उन दोनों की गति के लिए एक ही पैमाने पर दूरी-समय ग्राफ खीचें तथा व्याख्या करें।
सारणी 8.3. (पा. पु. पृ. स. 118)
फिरोज और सानिया द्वारा अपने साइकिलों पर अलग-अलग समय में तय की गई दूरी।
| समय | फिरोज के द्वारा तय की गई दरी KM | सानिया के द्वारा तय की गई दूरी KM |
| 8.00 am | 0 | 0 |
| 8.05 am | 1.0 | 0.8 |
| 8.10 am | 1.9 | 1.6 |
| 8.15 am | 2.8 | 2.3 |
| 8.20 am | 3.6 | 3.0 |
| 8.25 am | – | 3.6 |
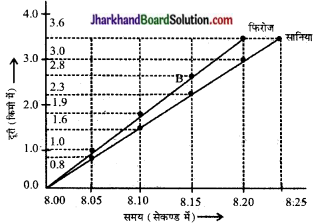
खण्ड 8.4 से सम्बन्धित पाठ्य-पुस्तक के प्रश्नेत्तर (पा. पु. पृ. सं. 118)
प्रश्न 1.
किसी वस्तु की एकसमान व असमान गति के लिए समय-दूरी ग्राफ की प्रकृति क्या होती है?
उत्तर:
एकसमान गति-एकसमान गति के लिए समय-दूरी ग्राफ एक सरल रेखा होता है।
असमान गति – असमान गति में समय दूरी ग्राफ सरल रेखा नहीं होता है। यह एक वक्र हो सकता है। कई अलग- अलग वक्र तथा सरल रेखाओं से मिलकर बना हो सकता है।
प्रश्न 2.
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका दूरी- समय ग्राफ, समय अक्ष के समान्तर एक सरल रेखा है?

उत्तर:
दूरी समय ग्राफ का समय अक्ष के समान्तर सरल रेखा होना यह प्रदर्शित करता है कि वस्तु की निर्देश बिन्दु से दूरी, समय के साथ परिवर्तित नहीं हो रही है अर्थात् समय के साथ वस्तु की स्थिति बदल नहीं रही है। इसका अर्थ यह है कि वस्तु गतिमान नहीं है अर्थात् स्थिर है। (देखिए चित्र 8.14)
![]()
प्रश्न 3.
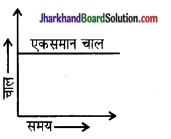
किसी वस्तु की गति के विषय में आप क्या कह सकते हैं, जिसका चाल-समय ग्राफ, अक्ष के समान्तर एक सरल रेखा है?
उत्तर:
चाल- समयग्राफ का समय अक्ष के समान्तर एक सरल रेखा होना यह प्रदर्शित करता है कि वस्तु की चाल समय के साथ परिवर्तित नहीं हो रही है। अर्थात् चाल स्थिर है। अतः वस्तु एकसमान चाल से गतिमान है। (देखिए fast 8.15)
प्रश्न 4.
वेग समय ग्राफ के नीचे के क्षेत्र में मापी गई राशि क्या होती है?
उत्तर:
वेग-समय ग्राफ के नीचे के क्षेत्र से एक दिए गए समयान्तराल में वस्तु द्वारा तय की गई दूरी ज्ञात होती है।
खण्ड 8.5 से सम्बन्धित पाठ्य पुस्तक के प्रश्नोत्तर (पा.पु. पू. सं. 121)
प्रश्न 1.
कोई बस विरामावस्था से चलना प्रारम्भ करती है तथा 2 मिनट तक 0-1 मीटर/सेकण्ड के एकसमान त्वरण से चलती है। परिकलन कीजिए-
(a) प्राप्त की गई चाल, (b) तय की गई दूरी।
हल:
दिया है:
u = 0, त्वरण a = 0.1 मीटर / सेकण्ड²
समय t = 2 मिनट = 2 x 60 = 120 सेकण्ड
(a) सूत्र vu + gt से,
प्राप्त की गई चाल x 120 सेकण्ड = 0 + 0.1 (मी / से-) = 12 मीटर / सेकण्ड।
(b) s = ut + \(\frac { 1 }{ 2 }\) at² ar से तय की गई दूरी
s = 0 × 120 + \(\frac { 1 }{ 2 }\) x 0.1 x 120 x 120
= 720 मीटर।
प्रश्न 2.
कोई रेलगाड़ी 90 किमी / घन्टा की चाल से चल रही है। ब्रेक लगाए जाने पर वह – 0.5 मीटर / सेकण्डर² का एकसमान त्वरण उत्पन्न करती है। रेलगाड़ी विरामावस्था में जाने से पहले कितनी दूरी तय करेगी ?
हल:
दिया है : u = 90 किमी / घण्टा
= 90 × \(\frac { 5 }{ 18 }\) = 25 मीटर / सेकण्ड
a = – 0.5 मीटर / सेकण्डर²
रुक जाने पर v = 0, तय दूरी s = ?
सूत्र v² – u² = 2as से
0² – ( 25)² – 2 × (0.5) × 3 या 625 = – s
अतः तय की गई दूरी 625 मीटर।
प्रश्न 3.
एक ट्राली एक आनत तल पर 2 मीटर/सेकण्डर के त्वरण से नीचे जा रही है। गति प्रारम्भ करने के 3 सेकण्ड के पश्चात् उसका वेग क्या होगा?
हल:
दिया है : u = 0 a = 2 मीटर / सेकण्डर²
t = 3 सेकण्ड, v = ?
सूत्र v = u + at से,
3 सेकण्ड बाद, वेग = 0 + 2 × 3 = 6 मीटर / सेकण्ड।
प्रश्न 4.
एक रेसिंग कार का एकसमान त्वरण 4 मीटर / सेकण्ड है। गति प्रारम्भ करने के 10 सेकण्ड के पश्चात् वह कितनी दूरी तय करेगी?
हल:
दिया है गति के प्रारम्भ में u = 0, त्वरण a = 4 मीटर / सेकण्ड 2, समय t = 10 सेकण्ड दूरी s = ?
सूत्र
S = ut + \(\frac { 1 }{ 2 }\) at² से,
तय दूरी
s = 0 × 10 + \(\frac { 1 }{ 2 }\) × 4 × (10)²
= 2 × 100
या s = 200 मीटर
प्रश्न 5.
किसी पत्थर को ऊर्ध्वाधर ऊपर की ओर 5 मीटर / सेकण्ड के वेग से फेंका जाता है। यदि गति के दौरान पत्थर का नीचे की ओर दिष्ट त्वरण 10 मीटर / सेकण्ड है तो पत्थर के द्वारा कितनी ऊँचाई प्राप्त की गई तथा उसे वहाँ पहुँचने में कितना समय लगा?
हल:
दिया है पत्थर का वेग u = 5 मीटर / सेकण्ड, त्वरण a = 10 मीटर / सेकण्डर
[∵ त्वरण नीचे की ओर है अतः ऋणात्मक लिया गया है।]
माना कि पत्थर ऊँचाई तक पहुँचता है, वहाँ पहुँचने में उसे समय लगता है।
तब अधिकतम ऊँचाई पर s = h तथा v = 0
v² – u² = 2 as, 0² – (5)² = 2(-10) h
या – 25 = 20h या h = \(\frac { -25 }{ -20 }\) = \(\frac { 5 }{ 4 }\) मीटर
तथा v = u + at से 0 = 5 + (-10)t
या 10 t = 5 या t = = 0-5 सेकण्ड
अतः पत्थर द्वारा प्राप्त ऊँचाई h = 1.25 मीटर
तथा यह ऊँचाई प्राप्त करने में लिया गया समय t = 10.5 सेकण्ड।
![]()
क्रियाकलाप 8.11. (पा.पु. पृ. सं. 122)
एक धागे का टुकड़ा लेकर उसके एक छोर पर एक छोटे से पत्थर को बाँध दें धागे के दूसरे छोर को पकड़कर पत्थर को वृत्तीय मार्ग पर नियत चाल से घुमाया जाए। अब यदि पत्थर सहित धागे को छोड़ दिया जाए तब पत्थर किस दिशा में जाएगा। पत्थर को अलग-अलग स्थान पर पुनः छोड़ें तथा प्रेक्षण करें।
निष्कर्ष – पत्थर वृत्तीय पथ के स्पर्शी के अनुदिश सरल रेखीय पथ पर गति करता है। इसका कारण यह है कि जब पत्थर को छोड़ा जाता है तो वह उसी दिशा में गति जारी रखता है जिस दिशा में उस क्षण वह गति कर रहा है। जब किसी पत्थर को वृत्तीय पथ पर घुमाया जाता है तो उसकी गति की दिशा प्रत्येक बिन्दु पर परिवर्तित होती है।
उदाहरण – एथलीट चक्रिका (डिसकॅस) या गोले को फेंकते समय अपने शरीर को घुमाकर उसे वृत्तीय गति प्रदान करता है। इच्छित दिशा में गोला या चक्र उसी दिशा में गति करता है जिस दिशा में वह छोड़ते समय गति कर रहा था। इसके अन्य उदाहरण हैं- चन्द्रमा एवं पृथ्वी की गति, पृथ्वी के चारों ओर वृत्तीय कक्षा में घूर्णन करता हुआ एक उपग्रह, वृत्तीय पथ पर नियत चाल से चलता हुआ साइकिल सवार इत्यादि।