JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9

Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Exercise 13.9

प्रश्न 1.
एक लकड़ी के बुक – शैल्फ की बाहरी विमाएँ निम्न हैं:
ऊँचाई = 110 सेमी, गहराई = 25 सेमी, चौड़ाई = 85 सेमी (देखिए आकृति)।
प्रत्येक स्थान पर तख्तों की मोटाई 5 सेमी है। इसके बाहरी फलकों पर पॉलिश कराई जाती है और आन्तरिक फलकों पर पेण्ट किया जाना है। यदि पॉलिश कराने की दर 20 पैसे प्रति सेमी है और पेण्ट कराने की दर 10 पैसे प्रति सेमी है, तो इस बुक-शैल्फ पर पॉलिश और पेण्ट कराने का कुल व्यय ज्ञात कीजिए।
हल:

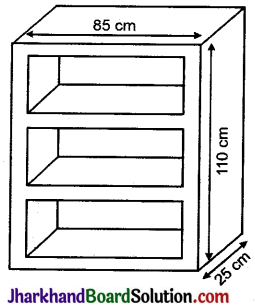
बुक शैल्फ समान लम्बाई, चौड़ाई तथा ऊँचाई वाले तीन घनाभाकार बॉक्स से बनी है।
हमें प्रत्येक बॉक्स का अलग-अलग पृष्ठीय क्षेत्रफल ज्ञात करना होगा।

बॉक्स की ऊँचाई:
शैल्फ की ऊँचाई = 110 सेमी तथा बीच में प्रत्येक 5 सेमी मोटाई के 4 तख्ते ऊँचाई में हैं।
तब बिना तख्तों के शैल्फ की ऊँचाई = (110 – 4 × 5 ) सेमी
= 90 सेमी
∴ बॉक्स की ऊँचाई = \(\frac{90}{3}\) सेमी = 30 सेमी

बॉक्स की लम्बाई :
इसी प्रकार शैल्फ की लम्बाई = 85 सेमी तथा दोनों ओर 2 तख्ते लम्बाई में हैं।
अतः बिना तख्तों के शैल्फ की लम्बाई = (85 – 2 × 5) सेमी = 75 सेमी
∴ प्रत्येक बॉक्स की लम्बाई = 75 सेमी

बॉक्स की चौड़ाई:
शैल्फ की चौड़ाई = 25 सेमी तथा इसमें केवल एक तख्ता है।
अतः बिना तख्ते के शैल्फ की चौड़ाई = (25 – 5) सेमी = 20 सेमी
∴ बॉक्स की चौड़ाई = 20 सेमी

बक्सों का पृष्ठीय क्षेत्रफल :
1 बॉक्स का पृष्ठीय क्षेत्रफल 2(lb + bh + hl)
= 2 (75 × 20 + 20 × 30 + 30 × 75) सेमी²
= 2(1500 + 600 + 2250) सेमी²
= 2 × 4350 = 8700 सेमी²
इस घनाभाकार शैल्फ में सामने की ओर का खुला 1 फलक सम्मिलित नहीं है।
∴ फलक का क्षेत्रफल = l × h
= 75 सेमी × 30 सेमी = 2250 सेमी²
बॉक्स का वास्तविक पृष्ठीय क्षेत्रफल = (8700 – 2250) = 6450 सेमी²
3 बाक्सों का पृष्ठीय क्षेत्रफल = 3 × 6450 = 19350 सेमी²
अतः आन्तरिक फलक का वक्र पृष्ठीय क्षेत्रफल = 19350 सेमी²
अतः 10 पैसे प्रति सेमी² की दर से पेण्ट करने का व्यय = 0.10 × 19350 = 1,935
सम्पूर्ण शैल्फ का वक्र पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (85 × 25 + 25 × 110 + 110 × 85 ) सेमी ²
= 2(2125 + 2750 + 9350) सेमी²
= 2 × 14225 = 28450 सेमी²
∴ शैल्फ सम्पूर्ण घनाभ न होकर सामने के तीन फलक खुले हुए हैं। इन तीन फलकों में से प्रत्येक फलक की लम्बाई 75 सेमी तथा चौड़ाई 30 सेमी है।
∴ 1 फलक का क्षेत्रफल = 75 × 30 सेमी²
= 2250 सेमी²
∴ 3 फलकों का क्षेत्रफल = 3 × 2250 सेमी²
= 6750 सेमी²
∴ शैल्फ का वास्तविक बाहरी क्षेत्रफल = (28450 – 6750) सेमी²
= 21700 सेमी²
20 पैसे प्रति वर्ग सेमी की दर से शैल्फ पर पॉलिश का खर्च = ₹ 0.20 × 21700 = ₹ 4,340
अतः पॉलिश और पेण्ट में कुल खर्च = ₹ (4,340 + 1,935)
= ₹ 6,275

प्रश्न 2.
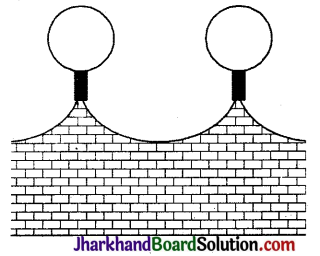
किसी घर के कम्पाउण्ड की सामने की दीवार को 21 सेमी व्यास वाले लकड़ी के गोलों को छोटे आधारों पर टिका कर सजाया जाता है, जैसा कि आकृति में दिखाया गया है। इस प्रकार के आठ गोलों का प्रयोग इस कार्य के लिए किया जाता है और इन गोलों को चाँदी वाले रंग में पेण्ट करवाना है। प्रत्येक आधार 1.5 सेमी त्रिज्या और ऊँचाई 7 सेमी का एक बेलन है तथा इन्हें काले रंग से पेण्ट करवाना है। यदि चाँदी के रंग का पेण्ट करवाने की दर 25 पैसे प्रति सेमी है तथा काले रंग के पेण्ट करवाने की दर 5 पैसे प्रति सेमी² हो, तो पेण्ट करवाने का कुल व्यय ज्ञात कीजिए।
हल:
बेलन की त्रिज्या (r) = 1.5 सेमी
तथा बेलन की ऊँचाई = 7 सेमी
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 1.5 × 7 सेमी² = 66 सेमी²

∴ 8 बेलनों का वक्रपृष्ठीय क्षेत्रफल = 8 × 66 सेमी²
= 528 सेमी²
काले रंग का पेण्ट करने वाले भाग का क्षेत्रफल = 528 सेमी²
∴ काले रंग करने का व्यय = ₹ 0.05 × ₹ 528
= ₹ 26.40
लकड़ी के गोले का व्यास = 21 सेमी
लकड़ी के गोले की त्रिज्या = \(\frac{21}{2}\) सेमी
लकड़ी के एक गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
= 1386 सेमी²
बेलनाकार आधार का पृष्ठीय क्षेत्रफल = πr²
= \(\frac{22}{7}\) × 1.5 × 1.5 सेमी²
= \(\frac{49.50}{7}\) सेमी²
= 7.1 सेमी² (लगभग)।
पेण्ट कराने के लिए आवश्यक क्षेत्रफल = 1386 – 7.1 = 1378.9 सेमी²
तथा 8 गोलों का पेण्ट कराने का क्षेत्रफल = 8 × 1378.9 सेमी²
= 11031.2 सेमी²
∴ चाँदी के रंग के पेण्ट का व्यय = ₹ 0.25 × ₹ 11031.2 = 2757.80
कुल पेण्ट कराने का व्यय = ₹ (26.40 + 2757.80)
= ₹ 2,784.20

प्रश्न 3.
एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है ?
हल:
गोले का व्यास = 100 सेमी
∴ त्रिज्या = \(\frac{100}{2}\) सेमी = 50 सेमी
पहले गोले का वक्र पृष्ठीय क्षेत्रफल = 4πr²
= 4π × 50 × 50 सेमी²
= 10000π सेमी²
गोले के व्यास में 25% की कमी हो जाती है।
∴ नये गोले का व्यास = 75 सेमी
∴ त्रिज्या = \(\frac{75}{2}\) सेमी
नवनिर्मित गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4π × \(\frac{75}{2} \times \frac{75}{2}\)सेमी²
= 5625π सेमी²
∴ क्षेत्रफल में कमी (10000π = 5625π) सेमी²
= 4375π सेमी²
अतः क्षेत्रफल में प्रतिशत कमी = \(\frac{4375 \pi}{10000 \pi} \times 100 \%\)
\(\frac{4375}{100} \%\) = 43.75%