JAC Class 9 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Jharkhand Board JAC Class 9 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

JAC Board Class 9th Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

प्रश्न 1.
यदि एक बेलन का वक्रपृष्ठ सिरों के क्षेत्रफल से दोगुना है तो उसकी ऊंचाई और त्रिज्या का अनुपात होगा :
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 2 : 3
हल :
माना बेलन की त्रिज्या r तथा ऊँचाई h है, तब वक्रपृष्ठ = 2 × सिरों का क्षेत्रफल
2πrh = 2 × 2πr²
h = 2r
\(\frac{h}{r}=\frac{2}{1}\) = 2 : 1
अत: विकल्प (C) सही है।

प्रश्न 2.
एक गोले का आयतन 36π घन सेमी है, तो उसकी त्रिज्या है:
(A) 3 सेमी
(B) 6 सेमी
(C) 2 सेमी
(D) 9 सेमी।
हल :
\(\frac {4}{3}\)πr³ = 36π
r³ = \(\frac{36 \times 3}{4}\) = 9 × 3
r = \(\sqrt{3 \times 3 \times 3}\) = 3 सेमी
अत: विकल्प (A) सही है।

प्रश्न 3.
किसी समकोण त्रिभुज की समकोण बनाने वाली किसी एक भुजा के परितः घुमाने पर निर्मित आकृति होगी
(A) बेलन
(B) प्रिज्म
(C) गोला
(D) शंकु
हल :
अत: विकल्प (D) सही है।

प्रश्न 4.
यदि दो शंकुओं की ऊंचाइयाँ बराबर हो तथा उनकी त्रिज्याओं का अनुपातः 4 : 7 हो तो उनके आयतनों का अनुपात होगा :
(A) 16 : 49
(B) 49 : 16
(C) 14 : 17
(D) 4 : 7
हल :
माना दोनों शंकुओं का त्रिज्याएँ क्रमशः 4x तथा 7x हैं:

= \(\frac {16}{49}\)
अतः सही विकल्प (A) है।

प्रश्न 5.
एक बेलनाकार बोतल का व्यास 10 सेमी है। यदि उसमें 14 सेमी ऊंचाई तक द्रव भरा हो, तो द्रव का आयतन है :
(A) 1200 घन सेमी
(B) 1100 घन सेमी
(C) 1500 घन सेमी
(D) 1150 घन सेमी।
हल :
बेलनाकार बोतल का व्यास = 10 सेमी
अतः बोतल की त्रिज्या (r) = व्यास / 2 = \(\frac {10}{2}\) = 5 सेमी
द्रव की ऊँचाई (h) = 14 सेमी
द्रव का आयतन = πr²h
= \(\frac {22}{7}\) × (5)² × 14 = \(\frac {22}{7}\) × 25 × 14
= 22 × 25 × 2 = 22 × 50
= 1100 घन सेमी
अत: सही विकल्प (B) है।

प्रश्न 6.
9 सेमी त्रिज्या के धातु के गोले को पिघलाकर 3 सेमी त्रिज्या और 6 सेमी ऊंचाई के शंकु बनाये जा सकने वाले शंकुओं की संख्या है :
(A) 54
(B) 45
(C) 55
(D) 44
हल :
9 सेमी त्रिज्या वाले गोले का आयतन
= \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × π × (9)³
= \(\frac {4}{3}\) × π × 9 × 9 × 9
= 4 × π × 3 × 81 घन सेमी
अब 3 सेमी त्रिज्या और 6 सेमी ऊँचाई वाले शंकु का आयतन
= \(\frac {1}{3}\)πr²h = \(\frac {1}{3}\) × π × (3)² × 6
= \(\frac {1}{3}\) × π × 9 × 6
= π × 3 × 6 = 18π घन सेमी
शंकुओं की संख्या = गोले का आयतन / शंकु का आयतन
= \(\frac{4 \times \pi \times 3 \times 81}{\pi \times 3 \times 6}\) = 54
= \(\frac {972π}{18π}\) = 54
अत: (A) विकल्प सही है।

प्रश्न 7.
यदि दो गोलों की त्रिज्याओं का अनुपात 2 : 3 है, तो उनके आयतन का अनुपात है:
(A) 7 : 8
(B) 8 : 27
(C) 4 : 9
(D) 1 : 27
हल :
माना दोनों गोलों की त्रिज्याएँ क्रमश: r₁ और r₂ है।
दिया है, दोनों गोलों की त्रिज्याओं का अनुपात = r₁ : r₂ = 2 : 3
⇒ \(\frac{r_1}{r_2}=\frac{2}{3}\)
दोनों गोलों के आयतनों का अनुपात

अतः दोनों गोलों के आयतनों का अनुपात 8 : 27 होगा।
अत: सही विकल्प (B) है।

प्रश्न 8.
एक तार का व्यास 5% कम कर दिया जाए तो उसकी लम्बाई कितने प्रतिशत बढ़ा दी जाए कि आयतन न बदले ?
(A) 10%
(B) 10.8%
(C) 4%
(D) 2.5%
हल :
माना तार का व्यास = x सेमी
व्यास में कमी = 5%
नया व्यास \(\frac{95 x}{100}=\frac{19}{20}\)
तथा त्रिज्या = \(\frac {19}{40}\)x
माना त्रिज्याओं की कमी होने पर ऊँचाई h से बढ़कर h’ हो जाती है।
प्रश्नानुसार – π(\(\frac {19}{40}\)x)² h’ = π(\(\frac {x}{2}\))² h

प्रश्न 9.
एक लम्बवृत्तीय बेलन का आयतन 175π घन सेमी और ऊँचाई 7 सेमी है, तो उसका व्यास होगा।
(A) 5 सेमी
(B) 25 सेमी
(C) 10 सेमी
(D) 7 सेमी
हल :
बेलन का आयतन = πr²h
= 175π
r² × 7 = 175
r² = \(\frac {175}{7}\) = 25
r = \(\sqrt{25}\) = 25 सेमी
व्यास = 2 × r = 2 × 5 = 10 सेमी
अतः विकल्प (C) सही है।

प्रश्न 10.
यदि नल का बाहरी व्यास तथा भीतरी व्यास क्रमशः 4 सेमी तथा 3 सेमी और ऊंचाई 20 सेमी है, तो आयतन होगा। नल का आयतन = π(r₁r² – r₂r²)h
(A) π(4² – 3²) 20
(B) π[(2)² – (1.5)²]20
(C) π(4 – 3) 20
(D) π(2 – 1.5) 20.
हल :
नल का बाहरी व्यास तथा भीतरी व्यास क्रमश: 4 सेमी तथा 3 सेमी है।
∴ उसकी बाहरी तथा भीतरी त्रिज्याएँ क्रमशः \(\frac {4}{2}\) = 2
सेमी और \(\frac {3}{2}\) = 1.5 है।
अत: विकल्प (B) सही है।

प्रश्न 11.
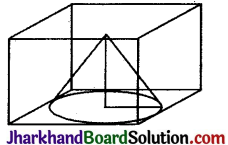
14 सेमी भुजा के एक घन में से एक बड़े से बड़ा शंकु काटा जाता है। शंकु का आयतन होगा :

(A) 766.18 घन सेमी
(B) 817.54 घन सेमी
(C) 1232 घन सेमी
(D) 718.66 घन सेमी।
हल :
14 सेमी भुजा के घन से बड़े से बड़ा शंकु काटा जाता है।
अतः शंकु की ऊँचाई (h) = 14 सेमी
शंकु के आधार का व्यास = 14 सेमी
अतः शंकु की त्रिज्या = व्यास / 2 = \(\frac {14}{2}\) = 7 सेमी
शंकु का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × (7)² × 14
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 7 × 7 × 14
= \(\frac {22}{3}\) × 7 × 14
= \(\frac{22 \times 98}{3}=\frac{2156}{3}\)
= 718.66 घन सेमी
अत: सही विकल्प (D) है।

प्रश्न 12.
एक लम्बवृत्तीय बन्द बेलन के आधार की त्रिज्या r और ऊँचाई h हो, तो उसके सभी पृष्ठों पर रंग कराने के लिए क्षेत्रफल होगा:
(A) 2πrh
(B) 2π(h + r)r
(C) πr²h
(D) 2πrh + πr².
हल :
बेलन के सभी पृष्ठों पर रंग कराने के लिए सम्पूर्ण पृष्ठीय क्षेत्रफल = 2π(h + r) r
अंत: सही विकल्प (B) है।

प्रश्न 13.
एक बेलन का आधार 625 वर्ग सेमी उसकी ऊँचाई 10 सेमी है, तो बेलन का आयतन होगा :
(A) 62.5 सेमी³
(B) 1320 सेमी³
(C) 6250 सेमी³
(D) 125 सेमी।³
हल :
बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= 625 × 10 = 6250 सेमी³
अत: सही विकल्प (C) है।

प्रश्न 14.
एक शंकु के आधार की त्रिज्या 7 सेमी और ऊंचाई 24 सेमी है। शंकु का पृष्ठीय क्षेत्रफल होगा :
(A) 25 सेमी²
(B) 550 सेमी²
(C) 189.6 सेमी²
(D) 134.09 सेमी²
हल :
दिया है,
शंकु के आधार की त्रिज्या (r) = 7 सेमी
और शंकु की ऊँचाई (h) = 24 सेमी
शंकु की तिर्यक ऊँचाई (l) = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(24)^2+(7)^2}\) = \(\sqrt{576+49}\)
= \(\sqrt{625}\)
शंकु की तिर्यक ऊँचाई (l) = 25 सेमी।
शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl
= \(\frac {22}{7}\) x 7 x 25 = 22 × 25 550 वर्ग सेमी
अत: विकल्प (B) सही है।

प्रश्न 15.
यदि एक गोले का पृष्ठीय क्षेत्रफल 616 वर्ग सेमी हो तो उसकी त्रिज्या होगी :
(A) 7 सेमी
(B) 6 सेमी
(C) 4.5 सेमी
(D) 7.2 सेमी
हल
माना गोले की त्रिज्या r है।
गोले का पृष्ठीय क्षेत्रफल 616 वर्ग सेमी
4πr² = 616
⇒ r² = \(\frac{616}{4 \pi}=\frac{616 \times 7}{4 \times 22}\) = 7 × 7
⇒ r = \(\sqrt{7 \times 7}\)
∴ r = 7 सेमी।
अत: सही विकल्प (A) है

प्रश्न 16.
एक शंकु, अर्द्धगोला और बेलन एक ही आधार और समान ऊँचाई पर बने हैं। उनके आयतनों का अनुपात होगा :
(A) 2 : 1 : 3
(B) 1 : 2 : 3
(C) 3 : 1 : 2
(D) 1 : 3 : 2
हल :
माना शंकु, अर्द्ध त्रिज्या तथा बेलन की समान (एक ही आधार) r है गोला तथा ऊँचाई h है।
तब शंकु का आयतन V₁ = \(\frac {1}{3}\)πr²h
अर्द्ध गोले का आयतन V₂ = \(\frac {2}{3}\)πr³ = \(\frac {2}{3}\)πr²(h)
[∵ अर्द्ध-गोले में r = h]
= \(\frac {2}{3}\)πr²h
बेलन का आयतन V₃ = πr²h
V₁ : V₂ : V₃ = \(\frac {1}{3}\)πr²h : \(\frac {2}{3}\)πr²h : πr²h
= \(\frac {1}{3}\) : \(\frac {2}{3}\) : 1 = \(\frac {1}{3}\) × 3 : \(\frac {2}{3}\) × 3 : 1 × 3
V₁ : V₂ : V₃ = 1 : 2 : 3
अतः सही विकल्प (B) हैं।

प्रश्न 17.
सीसे के एक घन की कोर 11 सेमी है। घन को पिघलाकर 1 सेमी व्यास की गोलियाँ बनाई जा सकती हैं:
(A) 2541
(B) 2154
(C) 5245
(D) 1245.
हल :
घन का आयतन = (कोर)³
= (11)³ = 1331 घन सेमी
1 सेमी व्यास की गोली की त्रिज्या = व्यास / 2
गोली की त्रिज्या = \(\frac {1}{2}\) = 0.5 सेमी

प्रश्न 18.
एक लोहे के पाइप की लम्बाई 20 सेमी तथा बाह्य व्यास 25 सेमी है। यदि पाइप की मोटाई 1 सेमी हो, तो पाइप का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :
माना पाइप की बाह्य और अन्तः त्रिज्याएँ क्रमशः व हैं।
बाह्य त्रिज्या (r₁) = 12.5 सेमी
अन्तः त्रिज्या (r₂) = (बाह्य त्रिज्या – मोटाई)
= (12.5 – 1) = 11.5 सेमी
पाइप की लम्बाई (h) = 20 सेमी
अतः पाइप का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2π(r₁ + r₂) (h + r₁ – r₂)
= 2 × \(\frac {22}{7}\) × (12.5 + 11.5) × (20 + 12.5 – 11.5) वर्ग सेमी
= 2 × \(\frac {22}{7}\) × 24 × 21 वर्ग सेमी
= 3168 वर्ग सेमी।

प्रश्न 19.
एक बेलन की त्रिज्या और ऊँचाई का अनुपात 5 : 7 तथा इसका आयतन 550 घन सेमी है। बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
हल :
बेलन की त्रिज्या ऊँचाई = 5 : 7
माना बेलन की त्रिज्या 5r तथा ऊँचाई 7r है।
बेलन का आयतन = 550 घन सेमी
⇒ πr²h = 550
⇒ \(\frac {22}{7}\) × (5r)² × 7r = 550
⇒ 22 × 25r³ = 550
⇒ 550r³ = 550
⇒ r³ = 1
∴ r = 1 सेमी
बेलन की त्रिज्या (r) = 5 सेमी और ऊँचाई (h) = 7
∴ बेलन का सम्पूर्ण पृष्ठ = 2r (h+r) r
= 2 × \(\frac {22}{7}\) × (7 + 5) × 5
= 2 × \(\frac {22}{7}\) × 12 × 5
= \(\frac {2640}{7}\) वर्ग सेमी
= 377.14 वर्ग सेमी।

प्रश्न 20.
एक हॉल 15 मीटर लम्बा और 12 मीटर चौड़ा है। यदि हाल के फर्श तथा छत के क्षेत्रफलों का योग उसकी चारों दीवारों के क्षेत्रफलों के योग के बराबर हो तो उस हॉल का आयतन ज्ञात कीजिए।
हल :
हाल के फर्श की लम्बाई (l) = 15 मीटर
तथा चौड़ाई (h) = 12 मीटर
फर्श का क्षेत्रफल = l × b = 15 × 12 = 180 मीटर²
क्योंकि छत का क्षेत्रफल = फर्श का क्षेत्रफल
∴ हॉल के फर्श का क्षेत्रफल + छत का क्षेत्रफल
= 180 + 180 = 360 मीटर
माना हॉल की ऊँचाई = h मीटर
चारों दीवारों का क्षेत्रफल = 2 (l + b) h मी²
= 2 (15 + 12) × h
= 54 h मी²
मौ प्रश्नानुसार, फर्श और छत के क्षेत्रफलों का योग = चारों भुजाओं के क्षेत्रफलों का योग
⇒ 360 मी² = 54 h मी²
h = \(\frac {360}{54}\)
हाल का आयतन = lbh
= 15 × 12 × \(\frac {20}{3}\)मी³
= 1200 घन मीटर

प्रश्न 21.
यदि शंकु के आधार की त्रिज्या 21 सेमी तथा ऊंचाई 28 सेमी हो, तो शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए।
हल :
शंकु के आधार की त्रिज्या (r) = 21 सेमी
ऊँचाई (h) = 28 सेमी
माना शंकु की तिर्यक ऊँचाई l सेमी है, तब
l² = h² + r²
∴ l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(28)^2+(21)^2}\) सेमी
= \(\sqrt{784+441}\) सेमी
= \(\sqrt{1225}\) = 35 सेमी

(i) अत: शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = π(l + r)r
= \(\frac {22}{7}\)(35 + 21) × 21 वर्ग सेमी
= \(\frac {22}{7}\) × 56 × 21 वर्ग सेमी ।
= 3696 वर्ग सेमी

(ii) शंकु का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × (21)² × 28 घन सेमी
= \(\frac {1}{3}\) × \(\frac {22}{7}\) × 21 × 21 × 28 घन सेमी
= 12936 घन सेमी।

प्रश्न 22.
एक टेन्ट शंकु के आकार का है, जिसके आधार की त्रिज्या 7 मीटर तथा ऊंचाई 5 मीटर है। टेन्ट में लगने वाले कपड़े का क्षेत्रफल ज्ञात कीजिए।
हल :
टेन्ट के आधार की त्रिज्या (r) = 7 मीटर
ऊँचाई (h) = 5 मीटर
∴ टेन्ट की तिर्यक ऊँचाई (l) = \(\sqrt{h^2+r^2}\)
l = \(\sqrt{(5)^2+(7)^2}\) मीटर
= \(\sqrt{25+49}\) = \(\sqrt{74}\) = 8.6 मीटर (लगभग).
अतः टेन्ट में लगने वाले कपड़े का क्षेत्रफल = πrl
= \(\frac {22}{7}\) × 7 × 8.6 वर्ग मीटर
= 189.2 वर्ग मीटर ।

प्रश्न 23.
एक धातु के गोले की त्रिज्या 14 सेमी है। इसका पृष्ठीय क्षेत्रफल और आयतन ज्ञात कीजिए ।
हल :
गोले की त्रिज्या (r) = 14 सेमी
अतः गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac {22}{7}\) × 14 × 14
= 2464 वर्ग सेमी
∴ गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × \(\frac {22}{7}\) × 14 × 14 × 14
= 11498.67 घन सेमी

प्रश्न 24.
12 सेमी त्रिज्या वाला एक धातु का गोला पिघलाकर तीन छोटे गोले बनाए गए हैं। यदि उनमें से दो छोटे गोलों की त्रिज्याऐं 6 सेमी तथा 8 सेमी हों तो तीसरे गोले की त्रिज्या ज्ञात कीजिए।
हल :
बड़े गोले की त्रिज्या = 12 सेमी
∴ आयतन = \(\frac {4}{3}\)πr³ = \(\frac {4}{3}\) × π × 12 × 12 × 12
= 2304π घन सेमी
नवनिर्मित तीन गोलियों में से एक की त्रिज्या = 8 सेमी
आयतन = \(\frac {4}{3}\)π × 8 × 8 × 8
= \(\frac {2048}{3}\)π घन सेमी
नवनिर्मित दूसरी गोली की त्रिज्या = 6 सेमी
आयतन = \(\frac {4}{3}\)π × 6 × 6 × 6
= 288π घन सेमी
इन दोनों गोलियों के आयतनों का योग = \(\frac {2048}{3}\)π + 288π
= \(\frac{2048 \pi+864 \pi}{3}\)
= \(\frac {2912}{3}\)π घन सेमी
तीसरी गोली का आयतन = बड़ी गोली का आयतन – दो गोलियों के आयतन का योग
= 2304π – \(\frac {2912}{3}\)π घन सेमी
= \(\frac {4000}{3}\)π घन सेमी
माना इस गोली की त्रिज्या = R
तब \(\frac {4}{3}\)πR³ = \(\frac {4000}{3}\)π
R³ = \(\frac {4000}{4}\) = 1000
R = \(\sqrt{1000}\) = 10
अतः तीसरी गोली की त्रिज्या = 10 सेमी

प्रश्न 25.
त्रिज्या 21 सेमी वाले एक अर्द्ध-गोले के लिए, ज्ञात कीजिए :
(i) चक्र पृष्ठीय क्षेत्रफल
(ii) कुल पृष्ठीय क्षेत्रफल ।
हल :
(i) त्रिज्या = 21 सेमी
अर्द्ध-गोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²
= 2 × \(\frac {22}{7}\) × 21 × 21 सेमी²
= 2772 सेमी² ।

(ii) अर्द्ध-गोले का कुल पृष्ठीय क्षेत्रफल = 3πr²
= 3 × \(\frac {22}{7}\) × 21 × 21 सेमी²
= 4158 सेमी² ।

प्रश्न 26.
किसी गोले की त्रिज्या 10 सेमी है। यदि त्रिज्या को 5% बढ़ा दिया जाए तो आयतन में कितने प्रतिशत की वृद्धि होगी ?
हल :
गोले की त्रिज्या = 10 सेमी
त्रिज्या में 5% की वृद्धि होने पर नयी त्रिज्या
= \(\frac {105}{100}\) × 10 = 10.5 सेमी
जब त्रिज्या 10 सेमी तो आयतन = \(\frac {4}{3}\)π(10)³
= \(\frac {88000}{21}\)घन सेमी

प्रश्न 27.
24 सेमी ऊँचे और 7 सेमी आधार की त्रिज्या के बेलन में उसी ऊँचाई और उसी आधार त्रिज्या का एक शंक्वाकार छिद्र किया जाता है। बचे हुए बेलनाकार सम्पूर्ण पृष्ठ और आयतन ज्ञात कीजिए ।

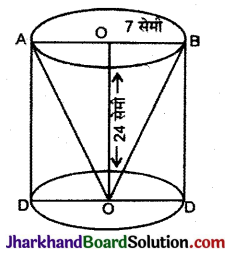
हल :
ठोस बेलन का आयतन = πr²h
= π(7)² × 24 घन सेमी
= π × 49 × 24 घन सेमी
= 1176π घन सेमी
शंक्वाकार छिद्र का आयतन = \(\frac {1}{3}\)πr²h
= \(\frac {1}{3}\) × π(7)² × 24
= π × 49 × 8 घन सेमी
= 392 π घन सेमी

शेष बेलन का आयतन = (1176π – 392π)
= 784π घन सेमी
= 784 × \(\frac {22}{7}\)घन सेमी
= 112 × 22
= 2464 घन सेमी

ठोस बेलन का वक्रपृष्ठ = 2πrh
= 2 × \(\frac {22}{7}\) × 7 × 24 वर्ग सेमी
= 44 × 24 वर्ग सेमी
= 1056 वर्ग सेमी
शंक्वाकार छिद्र के कारण ठोस का वक्रपृष्ठ उतना ही बढ़ जाएगा जितना कि छिद्र का वक्र पृष्ठ है।
∴ शंक्वाकार छिद्र की तिरछी ऊँचाई
l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{24^2+7^2}\)
= \(\sqrt{576+49}\)
= \(\sqrt{625}\)
l = 25 सेमी
शंक्वाकार छिंद्र का वक्र पृष्ठ = πrl
= \(\frac {22}{7}\) × 7 × 25
= 22 × 25 = 550 वर्ग सेमी

बेलन का सम्पूर्ण पृष्ठ = 1056 + 550 + πr²
= 1056 + 550 + \(\frac {22}{7}\) × 7 × 7 वर्ग सेमी
= 1056 + 550 + 154 वर्ग सेमी
= 1760 वर्ग सेमी
अतः बेलन का सम्पूर्ण पृष्ठ = 1760 वर्ग सेमी
आयतन = 2464 घन सेमी

प्रश्न 28.
एक समद्विबाहू समकोण त्रिभुज में कर्ण 4 सेमी लम्बा है। यदि त्रिभुज के कर्ण को अक्ष मानकर उसके परितः घुमाया जाए, तो निर्मित आकृति का वक्र आयतन ज्ञात कीजिए।
हल :

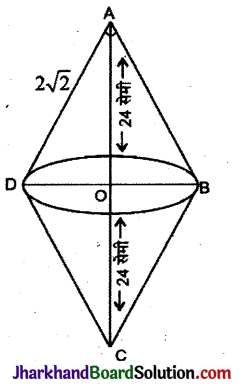
4 सेमी कर्ण वाले समद्विबाहु समकोण त्रिभुज ABC को कर्ण AC के परितः घुमाने से एक उभयनिष्ठ आधार वाला द्विशंकु बनेगा। प्रत्येक शंकु की ऊँचाई कर्ण की आधी \(\frac {4}{2}\) = 2
सेमी होगी। हम जानते हैं कि समकोण त्रिभुज में समकोण वाले शीर्ष को कर्ण के मध्य बिन्दु से मिलाने वाली रेखा की आधी होती है।
यह समकोण समद्विबाहु त्रिभुज है।
यह रेखा कर्ण पर भी होगी। यह रेखा ही शंकु की त्रिज्या है।
अतः त्रिज्या r = 2 सेमी
तिर्यक ऊँचाई l = \(\sqrt{2^2+2^2}\) = \(\sqrt{8}\)
= 2\(\sqrt{2}\) सेमी
वक्र पृष्ठ = 2 × एक शंकु का वक्रपृष्ठ
= 2 × πrl
= 2 × π × 2 × 2\(\sqrt{2}\)
= 8\(\sqrt{2}\)π वर्ग सेमी
ठोस का आयतन = 2 × एक शंकु का आयतन
= 2 × \(\frac {1}{3}\)πr²h
= 2 × \(\frac {1}{3}\) × π × 2 × 2\(\sqrt{2}\)
= \(\frac {16}{3}\)π घन सेमी

प्रश्न 29.
एक शंकु के आकार के बर्तन की त्रिज्या 10 सेमी और ऊंचाई 18 सेमी है, पानी से पूरा भरा हुआ है। इसे 5 सेमी त्रिज्या के एक बेलनाकार बर्तन में उड़ेला जाता है। बेलनाकार बर्तन में पानी की ऊंचाई ज्ञात कीजिए।
हल :
शंकु के आकार के बर्तन की त्रिज्या (r) = 10 सेमी
बर्तन की ऊँचाई (h) = 18 सेमी
शंकु के आकार के बर्तन का आयतन = \(\frac {1}{3}\) × πr²h
= \(\frac {1}{3}\) × π × (10)² × 18
= \(\frac {1}{3}\) × π × 100 × 18
= π × 100 × 6 = 600π घन सेमी
माना बेलनाकार बर्तन में पानी की ऊँचाई H सेमी है।
बेलनाकार बर्तन की त्रिज्या (R) = 5 सेमी
अब प्रश्नानुसार,
बेलनाकार बर्तन का आयतन = शंकु के आकार के बर्तन का आयतन
⇒ πR²H = 600π
⇒ π(5)² × H = 600π
⇒ 25π × H = 600π
∴ H = \(\frac {600π}{25π}\)
= 24 सेमी।
अतः बेलनाकार बर्तन में पानी की ऊँचाई 24 सेमी है।

प्रश्न 30.
एक गोले की त्रिज्या 4.2 सेमी है। गोले का वक्रपृष्ठ और आयतन ज्ञात कीजिए।
हल :
दिया है, गोले की त्रिज्या (r) = 4.2 सेमी
अतः गोले का वक्रपृष्ठ = 4πr² = 4 × \(\frac {22}{7}\) × (4.2)²
= 4 × \(\frac {22}{7}\) × 4.2 × 4.2 = 44 × 22 × 0.6 × 4.2
= 88 × 2.52 = 221.76 वर्ग सेमी।
और गोले का आयतन = \(\frac {4}{3}\)πr³
= \(\frac{4}{3} \times \frac{22}{7}\) × (4.2)³
= \(\ frac{4}{3} \times \frac{22}{7}\) × 4.2 × 4.2 × 4.2
= 4 × 22 × 1.4 × 0.6 × 4.2
= 88 × 0.84 × 4.2 = 88 × 3.528
= 310.464 = 310.46 घन सेमी
अतः गोले का वक्रपृष्ठ 221.76 वर्ग सेमी
और आयतन 310.46 घन सेमी है।

प्रश्न 31.
एक अर्द्ध-गोले की त्रिज्या 3.5 सेमी है, तो इसका आयतन और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
दिया है,
अर्द्ध-गोले की त्रिज्या (r) = 3.5 सेमी
अर्द्ध-गोले का आयतन = \(\frac {2}{3}\)πr³
= \(\frac{2}{3} \times \frac{22}{7}\) × (3.5)³
= \(\frac{2}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 3.5
= \(\frac {2}{3}\) × 22 × 0.5 × 12.25
= \(\frac {2}{3}\) × 11 × 12.25
= \(\frac {269.5}{3}\) = 89.83 घन सेमी
अर्द्ध-गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 3πr² = 3 × \(\frac {22}{7}\) × (3.5)²
= 3 × \(\frac {22}{7}\) × 3.5 × 3.5 = 3 × 22 × 0.5 × 3.5
= 3 × 11 × 3.5 = 115.5 वर्ग सेमी
अतः अर्द्ध-गोले का आयतन 89.83 घन सेमी
और सम्पूर्ण पृष्ठीय क्षेत्रफल 115.5 वर्ग सेमी है।

प्रश्न 32.
एक रोलर की लम्बाई 2 मीटर और व्यास 1.4 मीटर है। ज्ञात कीजिए कि 5 चक्कर लगाने में रोलर कितना क्षेत्र समतल करेगा ?
हल :
रोलर की लम्बाई (h) = 2 मीटर
और रोलर का व्यास = 1.4 मीटर
अतः रोलर की त्रिज्या r = व्यास / 2 = \(\frac {1.4}{2}\) = 0.7 मीटर
1 चक्कर लगाने में तय क्षेत्रफल = वक्र पृष्ठीय का क्षेत्रफल
= 2πrh ⇒ 2 × \(\frac {22}{7}\) × 0.7 × 2
= 2 × 22 × \(\frac {1}{10}\) × 2 = \(\frac {88}{10}\) = 88 वर्ग मीटर
∴ 5 चक्कर में समतल किया क्षेत्र
= 8.8 × 5 = 44.0 वर्ग मीटर।

प्रश्न 33.
एक सन्दूक की माप 50 सेमी x 36 सेमी x 25 सेमी है। इस सन्दूक का कवर बनाने में कितने वर्ग सेमी कपड़े की आवश्यकता होगी?
हल :
सन्दूक की लम्बाई (l) = 50 सेमी
सन्दूक की चौड़ाई (b) = 36 सेमी
सन्दूक की ऊँचाई (h) = 25 सेमी
सन्दूक का कवर बनाने के लिए उसके सम्पूर्ण पृष्ठीय क्षेत्रफल के बराबर कपड़े की आवश्यकता होगी।
सन्दूक का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2 (lb + bh + hl)
= 2 (50 × 36 + 36 × 25 + 25 × 50)
= 2 (1800 + 900 + 1250)
= 2 (3950) वर्ग सेमी
= 7900 वर्ग सेमी।
अतः सन्दूक के कवर के लिए आवश्यक कपड़ा 7900 वर्ग सेमी।

प्रश्न 34.
सीसे के एक गोले की त्रिज्या 5 सेमी है। इससे 5 मिमी त्रिज्या की कितनी गोलियाँ बनायी जा सकती हैं ?
हल :
सीसे के बड़े गोले की त्रिज्या (R) = 5 सेमी
इस गोले का आयतन (V) = \(\frac {4}{3}\)πR³ = \(\frac {4}{3}\)π(5)³
= \(\frac {4}{3}\) × π × 5 × 5 × 5 घन सेमी
इस सीसे से निर्मित प्रत्येक गोली की त्रिज्या (r) = 5 मिमी
= \(\frac {5}{10}\) सेमी = 0.5 सेमी
निर्मित प्रत्येक छोटी गोली का आयतन = \(\frac {4}{3}\)πr³
= \(\frac {4}{3}\) × π × (0.5)³
= \(\frac {4}{3}\) × π × 0.5 × 0.5 × 0.5 घन सेमी

प्रश्न 35.
एक घनाभ के तीन आसन्न फलकों का क्षेत्रफल क्रमश: xy और 2 हैं। सिद्ध कीजिए कि घनाभ का आयतन \(\sqrt{xyz}\) है।
हल :
माना घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः
l, b और h है।
प्रश्नानुसार,
l × b = x …………..(i)
b × h =y …………..(ii)
और h × l = z …………..(iii)
समीकरण (i), (ii) और (iii) का गुणा करने पर,
l × b × b × h × h × l = x × y × z
⇒ l²b²h² = xyz
⇒ (lbh)² = xyz
⇒ lbh = \(\sqrt{xyz}\)
∴ घनाभ का आयतन = \(\sqrt{xyz}\) . इति सिद्धम्

प्रश्न 36.
एक शंकु, जिसकी ऊँचाई 24 सेमी और आधार की त्रिज्या 6 सेमी है, प्रतिमा बनाने वाली चिकनी मिट्टी से बनाया गया है। एक बच्चा उसको पुनः गोले का आकार देता है। गोले की त्रिज्या ज्ञात कीजिए ।
हल :
माना गोले की त्रिज्या R सेमी है।
शंकु की ऊँचाई (h) = 24 सेमी तथा शंकु के आधार की त्रिज्या (r) = 6 सेमी।
शंकु का आयतन = \(\frac {1}{3}\)πr²h = \(\frac {1}{3}\) × π × (6)² × 24
= π × 12 × 24 = 288π घन सेमी
निर्मित गोले का आयतन = शंकु का आयतन
⇒ \(\frac {4}{3}\)πR³ = 288π
⇒ \(\frac {4}{3}\) × R³ = 288
⇒ R³ = \(\frac{288 \times 3}{4}\) = 72 × 3 = 216
⇒ R³ = \(\sqrt[3]{216}\)सेमी
= \(\sqrt[3]{6 \times 6 \times 6}\) = 6
अतः गोले की त्रिज्या 6 सेमी है।

प्रश्न 37.
यदि एक गोले का आयतन 38808 घन सेमी है, तो गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
गोले का आयतन = 38808 घन सेमी
माना गोले की त्रिज्या = r
अतः गोले का आयतन
\(\frac {4}{3}\)πr³ = 38808
या r³ = \(\frac{38808 \times 3}{4 \pi}\)
= \(\frac{38808 \times 3 \times 7}{4 \times 22}\) = 9261 घन सेमी
= (21)³ घन सेमी
∴ r = 21 सेमी
अब गोले का पृष्ठीय क्षेत्रफल = 4πr²
= 4 × \(\frac {22}{7}\) × 21 × 21 वर्ग सेमी
= 5544 वर्ग सेमी।

प्रश्न 38.
2 सेमी त्रिज्या वाले एक बेलनाकार गिलास की ऊंचाई \(\frac {6}{π}\) सेमी है, तो उसमें कितना पानी आयेगा ?
हल :
बेलनाकार गिलास की त्रिज्या (r) = 2 सेमी
ऊँचाई (h) = \(\frac {6}{π}\)सेमी
गिलास में पानी का आयतन = बेलनाकार गिलास का आयतन
= πr²h
= π × (2)² × \(\frac {6}{π}\)
= π × 4 × \(\frac {6}{π}\)
= 24 घन सेमी.

प्रश्न 39.
50 सेमी × 36 सेमी माप की एक धातु की आयताकार चादर है। इसके प्रत्येक कोने से 8 सेमी भुजा का वर्ग काट कर निकाल दिया गया है। शेष चादर से खुला हुआ डिब्बा बनाया गया है। डिब्बे का आयतन ज्ञात कीजिए।
हल :
चादर की लम्बाई = 50 सेमी
तथा चौड़ाई = 36 सेमी

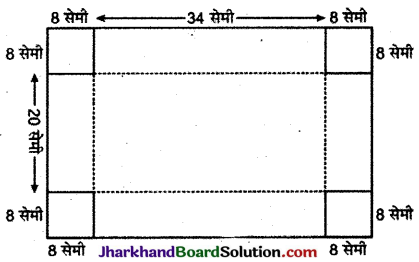
इस प्रकार चादर के प्रत्येक कोने से 8 सेमी भुजा के वर्ग काटे गये हैं तो
सन्दूक की लम्बाई (l) = 50 – 16 = 34 सेमी
सन्दूक की चौड़ाई (b) = 36 – 16 = 20 सेमी.
सन्दूक की ऊँचाई (h) = काटे गये वर्ग की भुजा
= 8 सेमी
∴ सन्दूक का आयतन ल. × चौ. × ऊ.
= 34 × 20 × 8
= 3.4 × 160
∴ आयतन = 5440 घन सेमी।

प्रश्न 40.
12 सेमी व्यास का एक गोलाकार भाग जल से अंशत: भरा हुआ है। यदि उसमें 6 सेमी व्यास का एक गोला पूर्णतः डुबो दिया जाता है। ज्ञात कीजिए कि बेलनाकार बर्तन में जल की सतह कितनी ऊंचाई तक उठ जायेगी।
हल :

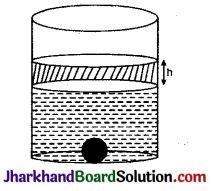
गोले का व्यास 6 सेमी
∴ गोले की त्रिज्या (r) = 3 सेमी
गोले का आयतन = \(\frac {4}{3}\)³
= \(\frac {4}{3}\) × π × 3 × 3 × 3
= 36π³
∴ गोले का आयतन = 36π घन सेमी
गोला डूबने पर अपने आयतन के बराबर पानी हटायेगा।
∴ हटे पानी का आयतन = 36π सेमी³
हटा पानी एक छोटा बेलनाकार भाग होगा, जैसा कि चित्र में दिखाया गया है।
बेलन की त्रिज्या (R) = \(\frac {12}{2}\) = 6
अतः R = 6 सेमी
माना हटाए गए पानी की ऊँचाई = h सेमी
अतः हटे पानी का आयतन = πR²h
अथवा πR²h = 36π
π(6)² × h = 36n
36h = 36
∴ h = \(\frac {36}{36}\) = 1 सेमी
अतः बडी ऊँचाई h = 1 सेमी. ।