Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 त्रिभुज Ex 6.4 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 6 त्रिभुज Exercise 6.4
प्रश्न 1.
मान लीजिए ΔABC ~ ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 हैं। यदि EF = 15.4 सेमी हो, तो BC ज्ञात कीजिए।
हल:
∵ ΔABC ~ ΔDEF (दिया गया है)
∴ Δ के क्षेत्रफलों का अनुपात = Δ की संगत भुजाओं के वर्गों का अनुपात
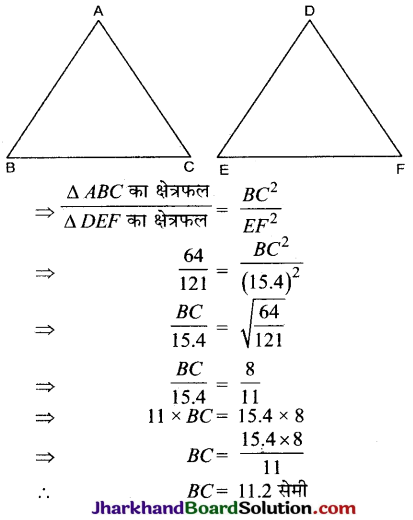
प्रश्न 2.
एक समलम्ब चतुर्भुज ABCD जिसमें AB || DC है, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। यदि AB = 2 CD हो, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल:
ABCD एक समलम्ब है जिसमें AB || DC है, के विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं तथा AB = 2CD हैं।
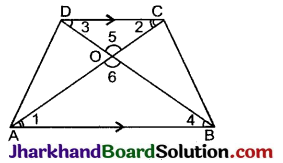
ΔAOB और ΔCOD में,
∠1 = ∠2 (एकान्तर कोण)
∠4 = ∠3 (एकान्तर कोण)
∠6 = ∠5 (शीर्षाभिमुख कोण)
कोण-कोण-कोण समरूपता गुणधर्म से
ΔAOB ~ ΔCOD (AAA समरूपता से)

अतः ΔAOB का क्षेत्रफल : ΔCOD का क्षेत्रफल
= 4 : 1
![]()
प्रश्न 3.
आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेदित करे, तो दर्शाइए कि 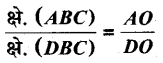 है।
है।
हल:
दिया है: ΔABC तथा ΔDBC एक ही आधार BC पर स्थित दो त्रिभुज हैं। AD, BC को बिन्दु O पर प्रतिच्छेद करता है।
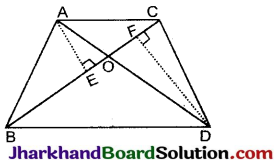
सिद्ध करना है:

रचना: शीर्ष A से BC पर AE तथा शीर्ष D से BC पर DF लम्य खींचा।
उपपत्ति: शीर्ष A तथा D से BC पर AE तथा DF लम्ब खींचे।
∴ ∠AEO = ∠DFO = 90°
समकोण ΔAEO तथा ΔDFO में,
∠AEO = ∠DFO (प्रत्येक 90°)
∠AOE = ∠DOF (शीर्षाभिमुख कोण)
A-A समरूपता गुणधर्म से,
ΔAEO ~ ΔDFO
⇒ \(\frac{A E}{D F}=\frac{A O}{D O}\) …(1)
अब ΔABC का क्षेत्रफल = \(\frac{1}{2}\)BC × AE
और ΔDBC का क्षेत्रफल = \(\frac{1}{2}\)BC × DF

प्रश्न 4.
यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों, तो सिद्ध कीजिए कि वे सर्वागसम होते हैं।
हल:
दिया है: ΔABC तथा ΔDEF समरूप हैं और ΔABC का क्षेत्रफल = ΔDEF का क्षेत्रफल
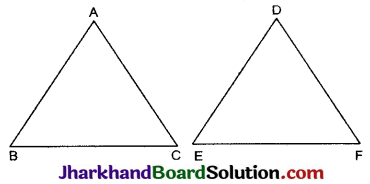
सिद्ध करना है: ΔABC ≅ ΔDEF
उपपत्ति: ∵ समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।

⇒ BC2 = EF2
⇒ BC = EF
अब ΔABC और ΔDEF में,
∠ABC = ∠DEF (∵ ΔABC ~ ΔDEF)
∠ACB = ∠DFE (∵ ΔABC ~ ΔDEF)
BC = EF (ऊपर सिद्ध किया है)
ΔABC ≅ ΔDEF (ASA सर्वांगसमता गुणधर्म से)
![]()
प्रश्न 5.
एक ΔABC की भुजाओं AB, BC और CA के मध्य बिन्दु क्रमश: D, E और F हैं। ΔDEF और ΔABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल:
दिया है: ΔABC की भुजाओं AB, BC और CA के मध्य बिन्दु क्रमश: D, E, F हैं जिनको मिलाने से ΔDEF बनता है।
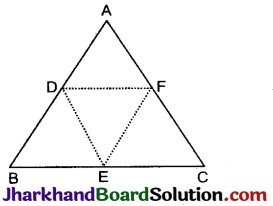
ज्ञात करना है:
ΔDEF का क्षेत्रफल: ΔABC का क्षेत्रफल
उपपत्ति: D, E, F क्रमश: AB, BC और CA के मध्य-बिन्दु हैं।
DE = \(\frac{1}{2}\)AC, DF = \(\frac{1}{2}\)BC तथा FE = \(\frac{1}{2}\)AB
⇒ \(\frac{D E}{A C}=\frac{D F}{B C}=\frac{E F}{A B}=\frac{1}{2}\)
ΔDEF ~ ΔABC (SSS समरूपता कसौटी से)

ΔDEF का क्षेत्रफल : ΔABC का क्षेत्रफलं
= 1 : 4
प्रश्न 6.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
हल:
दिया है: दो समरूप ΔABC और ΔDEF हैं। तथा AX और DY क्रमश: भुजाओं BC और EF की माध्यिकाएँ हैं।
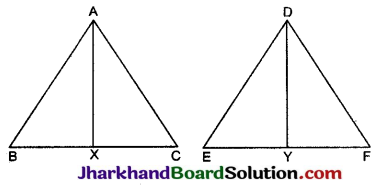

(∵ AX और DY माध्यिकाएँ हैं ∴ BC = 2BX, EF = 2EY)
⇒ \(\frac{A B}{D E}=\frac{B X}{E Y}\) …(1)
ΔABX और ΔDEY में,
∠B = ∠E (∵ ΔABC ~ ΔDEF)
\(\frac{A B}{D E}=\frac{B X}{E Y}\) (ऊपर सिद्ध किया है)
S-A-S समरूपता कसौटी से,
ΔABX ~ ΔDEY
\(\frac{A B}{D E}=\frac{A X}{D Y}\) …(2)
∵ दो समरूप त्रिभुज के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्ग के अनुपात के बराबर होता है।

![]()
प्रश्न 7.
सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
हल:
दिया है: ABCD एक वर्ग है जिसकी एक भुजा AB तथा विकर्ण AC है। AB तथा AC भुजा पर समबाहु ΔABE तथा ΔACF बनाए गए हैं।
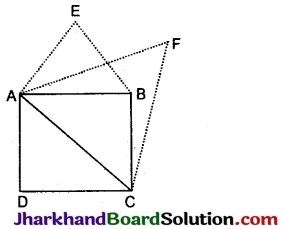
सिद्ध करना है: ΔABE का क्षेत्रफल = \(\frac{1}{2}\)ΔACF का क्षेत्रफल
उपपत्ति: समकोण त्रिभुज ABC में,
AC2 = AB2 + BC2, (पाइथागोरस प्रमेय से)
⇒ AC2 = AB2 + AB2 (∵ BC = AB)
⇒ AC2 = 2AB2
∴ AC = \(\sqrt{2}\)AB
भुजा AB पर बने समबाहु ΔABE का क्षेत्रफल = \(\frac{(A B)^2 \sqrt{3}}{4}\)
तथा विकर्ण AC पर बने समबाहु ΔACF का क्षेत्रफल = \(\frac{(A C)^2 \sqrt{3}}{4}\)

अतः ΔABE का क्षेत्रफल = \(\frac{1}{2}\)ΔACF का क्षेत्रफल
सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए:
प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य- बिन्दु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
हल:
ΔABC और ΔBDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य- बिन्दु है।
BD = \(\frac{1}{2}\)BC
या BC : BD = 2 : 1
⇒ AB : BD = 2 : 1
(∵ ΔABC एक समबाहु Δ है )
त्रिभुज ABC और त्रिभुज BDE में,
∠CAB = ∠DBE, ∠ABC = ∠BDE
तथा ∠ACB = ∠BED (प्रत्येक 60°)
∴ ΔABC ~ ΔBDE (AAA-समरूपता कसौटी)
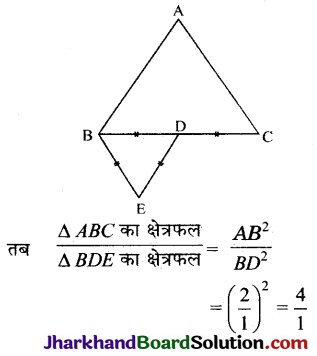
अतः ΔABC का क्षेत्रफल : ΔBDE का क्षेत्रफल
= 4 : 1
सही विकल्प (C) है।
![]()
प्रश्न 9.
दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है:
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
हल:
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात = भुजाओं के वर्ग का अनुपात
= (4 : 9)2
= 16 : 81
सही विकल्प (D) है।