JAC Class 10 Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
एक कक्षा में विद्यार्थियों को पंक्तियों में खड़ा किया जाता है। यदि एक पंक्ति में एक विद्यार्थी को अतिरिक्त खड़ा किया जाए तो पंक्तियों की संख्या 2 कम हो जाती है और यदि एक पंक्ति में एक विद्यार्थी कम खड़ा किया जाय तो पंक्तियों की संख्या 3 बढ़ जाती है। कक्षा कुल विद्यार्थियों की संख्या ज्ञात कीजिए।
हल :
माना कि मूल पंक्तियों की संख्या x है तथा मूलतः प्रत्येक पंक्ति में y विद्यार्थी खड़े किये जाते हैं।
विद्यार्थियों की कुल संख्या = x × y = xy
अब यदि एक पंक्ति में i विद्यार्थी अतिरिक्त खड़ा किया जाये तो एक पंक्ति में विद्यार्थियों की संख्या (y + 1) हो जायेगी तथा दिये गये प्रतिबन्ध से पंक्तियों की संख्या (x – 2) हो जायेगी।
अतः विद्यार्थियों की कुल संख्या
= (y + 1) (x – 2)
∴ (y + 1) (x – 2) = x × y
⇒ xy – 2y + x – 2 = xy
⇒ x – 2y = 2 ……..(1)
पुन: एक पंक्ति में एक विद्यार्थी कम खड़ा किया जाता है तो एक पंक्ति में विद्यार्थियों की संख्या (y – 1) होगी तथा प्रश्न में दिये गये प्रतिबन्ध के अनुसार पंक्तियों की संख्या (x + 3) हो जायेगी।
अतः विद्यार्थियों की कुल संख्या
= (y – 1) (x + 3)
∴ (y – 1) (x + 3) = xy
⇒ xy + 3y – x – 3 = xy
⇒ 3y – x – 3 = 0
⇒ x – 3y = – 3 ……..(2)
समीकरण (1) में से (2) को घटाने पर,

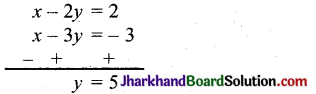
समीकरण (1) में y का मान रखने पर,
x – 2 × 5 = 2
⇒ x = 2 + 10
∴ x = 12
कक्षा में विद्यार्थियों की कुल संख्या = (xy)
= 12 × 5 = 60.

प्रश्न 2.
k का मान ज्ञात कीजिए ताकि निम्न समीकरण युग्म का कोई हल नहीं हो
(3k + 1)x + 3y – 2 = 0
(k² + 1)x + (k – 2)y – 5 = 0
हल :
दिए गए समीकरण युग्म का कोई हल नहीं होने के लिए प्रतिबन्ध

k = – 1 के लिए निम्न वक्तव्य सही है-
\(\frac{3}{k-2}\) ≠ \(\frac{2}{5}\)
अतः दिए गए समीकरण का कोई हल नहीं होगा। यदि k = – 1 है।

प्रश्न 3.
अशोक ने एक टेस्ट में 65 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 5 अंक मिले तथा प्रत्येक गलत उत्तर पर 2 अंक की कटौती की गई। यदि उसे सही उत्तर पर 3 अंक मिलते तथा प्रत्येक गलत उत्तर पर 1 अंक कटता, तो अशोक 40 अंक अर्जित करता। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए। टेस्ट में कुल कितने प्रश्न थे ?
हल :
माना अशोक द्वारा सही हल किये गये प्रश्नों की संख्या = x
गलत हल किये गये प्रश्नों की संख्या = y
बीज गणितीय निरूपण – पहली शर्त के अनुसार,
⇒ 5x – 2y = 65 …….(1)
दूसरी शर्त के अनुसार,
3x – y = 40 ……………(2)
ज्यामितीय निरुपण – समी. (1) से
5x – 2y = 65
x = \(\frac{65+2 y}{5}\)
y = – 5 रखने पर, x = \(\frac{65-10}{5}=\frac{55}{5}\) = 11
y = 0 रखने पर, x = \(\frac{65-0}{5}=\frac{65}{5}\) = 13
y = 5 रखने पर, x = \(\frac{65+10}{5}=\frac{75}{5}\) = 15
सारणी – I

x	11	13	15
y	-5	0	5

समी. (2) से
3x – y = 40
x = \(\frac{40+y}{3}\)
y = – 7 रखने पर x = \(\frac{40-7}{3}=\frac{33}{3}\) = 11
y = 2 रखने पर x = \(\frac{40+2}{3}=\frac{42}{3}\) = 14
y = 5 रखने पर y = \(\frac{40+5}{3}=\frac{45}{3}\) = 15

सारणी – II

x	11	14	15
y	-7	2	5

आलेख से स्पष्ट है कि दिए गए समीकरण युग्म की दो सरल रेखाऐं बिन्दु (10, 5) पर काटती है।
x = 10, y = 5
टेस्ट में प्रश्नों की संख्या
= 10 + 5 = 15.

प्रश्न 4.
x तथा y के लिए हल कीजिए-
27x + 31y = 85.
31x + 27y = 89.
हल :
दी गयी समीकरणं है-
27x + 31y = 85 ………….(1)
31x + 27y = 89 ………….(2)
समीकरण (1) तथा (2) को जोड़ने पर,

x का मान समीकरण (3) में रखने पर
2 + y = 3
⇒ y = 3 – 2 = 1
अतः x = 2 तथा y = 1 समीकरणों के अद्वितीय हल हैं।

प्रश्न 5.
एक तालाब को दो पाइपों द्वारा भरने में 12 घंटे लगते हैं। यदि बड़े व्यास वाले पाइप को 4 घन्टे तथा छोटे व्यास वाले पाइप को 9 घंटे प्रयोग किया जाता है तो तालाब का आधा भाग भरा जाता है। बताइये कितने समय में तालाब प्रत्येक पाइप द्वारा अलग-अलग भरा जायेगा।
हल :
माना बड़े व्यास वाला पाइप तालाब को x घंटे में तथा छोटे व्यास वाला पाइप y घंटे में भरता है।
∴ बड़े व्यास वाले पाइप द्वारा 1 घंटे में भस गया भाग = \(\frac{1}{x}\)
बड़े व्यास वाले पाइप द्वारा 4 घंटे भरा गया भाग = \(\frac{4}{x}\)
छोटे व्यास वाले पाइप द्वारा 1 घंटे में भरा गया भाग = \(\frac{1}{y}\)
छोटे व्यास वाले पाइप द्वारा 9 घंटे में भरा गया भाग = \(\frac{9}{y}\)
प्रश्नानुसार, \(\frac{4}{x}=\frac{9}{y}\) = \(\frac{1}{2}\) ……….(1)
और यदि दोनों पाइपों से तालाब 12 घंटे में भरा जाता है।
∴ \(\frac{12}{x}=\frac{12}{y}\) = 1 ……….(2)
माना कि \(\frac{1}{x}\) = a तथा \(\frac{1}{y}\) = b यह मान समीकरण (1) तथा (2) में रखने पर
4a + 9b = \(\frac{1}{2}\) ……….(3)
12a + 12b = 1 ……….(4)
समीकरण (3) को 3 से गुणा करके इसमें से समीकरण (4) को घटाने पर

अतः बड़े व्यास वाला पाइप 20 घन्टे तथा छोटे व्यास वाला पाइप 30 घंटे लेगा।

प्रश्न 6.
7 रबड़ और 5 पेन्सिलों का कुल मूल्य ₹ 58 है, जबकि 5 रबड़ और 6 पेन्सिलों का कुल मूल्य ₹ 56 है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए ।
हल :
माना 1 रबड़ का मूल्य ₹ x तथा एक पेन्सिल का मूल्य ₹ y है।
प्रश्नानुसार,
∴ 7x + 5y = 58
तथा 5 रबड़ और 6 पेन्सिलों का कुल मूल्य = ₹ 56
⇒ 7x + 5y = 56
बीजगणितीय निरूपण
7x + 5y = 58 ……(1)
5x + 6y = 56 …….(2)
ज्यामितीय निरूपण:
समीकरण (1) से,
7x + 5y = 58
⇒ 5y = 58 – 7x
⇒ y = \(\frac{58-7 x}{5}\)
x = 4 रखने पर, y = \(\frac{58-7 \times 4}{5}=\frac{58-28}{5}\) = 6
x = – 1 रखने पर y = \(\frac{58-7 \times(-1)}{5}=\frac{58+7}{5}\) = 13
सारणी – I

x	11	13
y	-5	0

समीकरण (2) से
5x + 6y = 56
⇒ 6у = 56 – 5x
⇒ y = \(\frac{56-5 x}{6}\)
x = – 2 रखने पर, y = \(\frac{56-5 \times(-2)}{6}=\frac{56+10}{6}\)
y = 11
x = 4 रखने पर y = \(\frac{56-5 \times 4}{6}=\frac{56-20}{6}\) = 6

सारणी – II

x	11	13
y	-5	0

सारणी I और सारणी II से प्राप्त x और y के मानों का आलेखन करने पर हमें निम्न आलेख प्राप्त होता है।

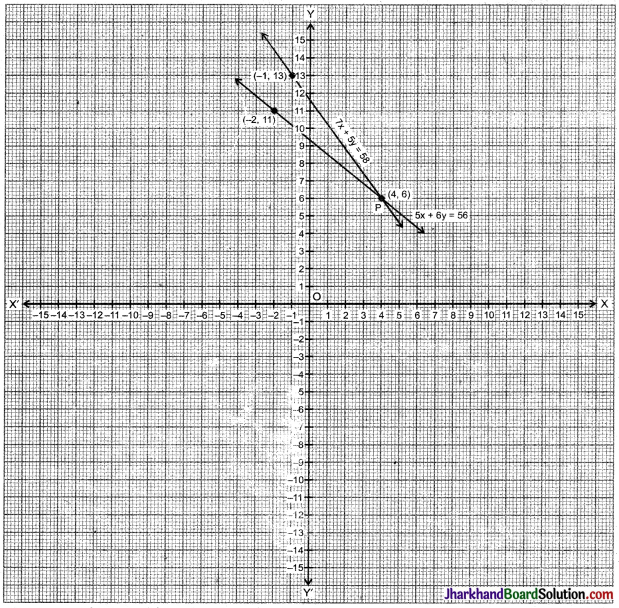
आलेख से स्पष्ट है कि दोनों रैखिक समीकरणों से प्राप्त सरल रेखाएँ बिन्दु P(4, 6) पर प्रतिच्छेदित होती हैं।
∴ x = 4 तथा y = 6
अतः एक रबड़ का मूल्य = ₹ 4 तथा एक पेन्सिल का मूल्य = ₹ 6

प्रश्न 7.
अभ्यास पुस्तिका और 3 पेन्सिलों का कुल मूल्य 17 रूपए है, जबकि 3 अभ्यास पुस्तिका और 4 पेन्सिलों का कुल मूल्य 24 रूपए है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए।
हल :
माना एक अभ्यास पुस्तिका का मूल्य ₹ x तथा एक पेन्सिल का मूल्य ₹ y है।
प्रश्नानुसार,
2 अभ्यास पुस्तिका और 3 पेन्सिलों का मूल्य = ₹ 17
⇒ 2x + 3y = 17
3 अभ्यास पुस्तिका और 4 पेन्सिलों का मूल्य 3x + 4y = ₹ 24
⇒ 3x + 4y = 24
बीजगणितीय निरूपण :
2x + 3y = 17 …….(1)
3x + 4y = 24 …….(2)
ज्यामितीय निरूपण :
समीकरण (1) से,
2x + 3y = 17
⇒ 3y = 17 – 2x
⇒ y = \(\frac{17-2 x}{3}\)
x = 1 रखने पर, y = \(\frac{17-2 \times 1}{3}=\frac{15}{3}\) = 5
x = 4 रखने पर, y = \(\frac{17-2 \times 4}{3}=\frac{9}{3}\) = 3
x = 7 रखने पर, y = \(\frac{17-2 \times 57}{3}=\frac{3}{3}\) = 1
सारणी – I

x	11	13	15
y	-5	0	5

समीकरण (2) से,
3x + 4y = 24
⇒ 4y = 24 – 3x
⇒ y = \(\frac{24-3 x}{4}\)
x = 0 रखने पर y = \(\frac{24-3 \times 0}{4}=\frac{24}{4}\) = 6
x = 4 रखने पर y = \(\frac{24-3 \times 4}{4}=\frac{12}{4}\) = 3
x = 8 रखने पर y = \(\frac{24-3 \times 8}{4}=\frac{0}{4}\) = 0

सारणी – II

x	11	13	15
y	-5	0	5

सारणी I और सारणी II से प्राप्त x और y के मानों का आलेखन करने पर हमें निम्न आलेख प्राप्त होता है :

आलेख से स्पष्ट है कि दोनों रैखिक समीकरणों से प्राप्त सरल रेखाएँ बिन्दु (4, 3) पर प्रतिच्छेद करती हैं।
∴ x = 4 तथा y = 3
अतः एक पुस्तिका का मूल्य = ₹ 4
तथा एक पेन्सिल का मूल्य = ₹ 3

प्रश्न 8.
एक रेलगाड़ी एक निश्चित दूरी एक समान चाल से तय करती है। यदि यह रेलगाड़ी 6 किमी / घंटा तेज चाल से चलती तो यह निश्चित समय से 4 घंटे कम लेती तथा यदि 6 किमी / घंटा धीमी चाल से चलती तो यह निश्चित समय से 6 घंटे अधिक लेती। यात्रा की निश्चित दूरी ज्ञात कीजिए।
हल :
माना रेलगाड़ी की चाल x किमी / घंटा तथा लिया गया समय y घंटे हैं।
∴ रेलगाड़ी द्वारा तय की गई दूरी = चाल × समय = x × y = xy किमी
तेज चलने पर रेलगाड़ी की चाल = (x + 6) किमी / घंटा
रेलगाड़ी द्वारा लिया गया समय = (y – 4) घंटे
अब, दूरी = (x + 6) (y – 4)
⇒ xy = xy – 4x + 6y – 24
⇒ 4x – 6y = – 24 ………..(1)
धीमी गति से चलने पर रेलगाड़ी की चाल = (x – 6) किमी / घंटा
समय = (y + 6) घंटे
अब, दूरी = चाल × समय
⇒ xy = (x – 6) × (y + 6)
⇒ xy = xy + 6x – 6y – 36
⇒ – 6x + 6y = – 36 ………..(2)
समीकरण (1) और समीकरण (2) को जोड़ने पर

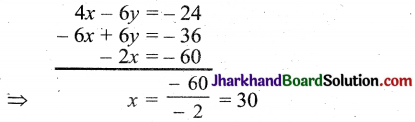
समीकरण (1) में x = 30 रखने पर
4 × 30 – 6y = 24
⇒ – 6y = – 24 – 120
⇒ y = \(\frac{-144}{-6}\) = 24
अत: रेलगाड़ी की चाल = 30 किमी / घंटा
रेलगाड़ी द्वारा लिया गया समय = 24 घंटे
तथा रेलगाड़ी द्वारा तय की गई दूरी = 30 × 24
= 720 किमी

प्रश्न 9.
दो संपूरक कोणों में से बड़े कोण का मान छोटे कोण के मान से 18° अधिक है। दोनों कणों के मान ज्ञात कीजिए ।
हल :
माना दिए गए कोण A तथा B हैं।
दिए है,
∠A = ∠B + 18° ………(i)
∵ ∠A व B संपूरक कोण हैं,
∴ ∠A + ∠B = 180°
[∵ संपूरक कोणों का योग 180° होता है]
समीकरण (i) से,
∠B + 18° + ∠B = 180°
2∠B = 162°
∠B = 81°
∴ अभीष्ठ ∠A = 81° + 18° = 99°
अतः अभीष्ट कोण 99° तथा 81° होगे।

प्रश्न 10.
सुमित की आयु उसके बेटे की आयु की तीन गुनी है। पाँच वर्षा के बाद, उसकी आयु अपने बेटे की आयु की ढ़ाई गुना हो जाएगी। इस समय सुमित की आयु कितने वर्ष है?
हल :
माना सुमित की वर्तमान आयु x वर्ष तथा उसके पुत्र की वर्तमान आयु y वर्ष है।
प्रश्नानुसार, x = 3y ………(i)
पाँच वर्ष बाद, सुमीत की आयु = (x + 5)
पाँच वर्ष बाद, पुत्र की आयु = (y + 5)
प्रश्नानुसार, x + 5 = 2\(\frac{1}{2}\)(y + 5) …………(ii)
समीकरण (i) का मान समीकरण (ii) में रखने पर,
3y + 5 = \(\frac{5}{2}\)(y + 5)
3y + 5 = \(\frac{5y}{2}=\frac{25}{2}\)
3y – \(\frac{5y}{2}\) = \(\frac{25}{2}\) – 5
\(\frac{6 y-5 y}{2}=\frac{25-10}{2}\)
\(\frac{y}{2}=\frac{15}{2}\)
समीकरण (i) से,
y = 15 वर्ष
x = 3 × 15 = 45 वर्ष
अतः सुमित की वर्तमान आयु 45 वर्ष तथा उसके पुत्र की वर्तमान आयु 15 वर्ष है।

प्रश्न 11.
एक पिता की आयु अपने दो बच्चों की आयु के योग के तीन गुने के समान है। 5 वर्ष के पश्चात् उसकी आयु बच्चों की आयु के योग के दुगुने के समान होगी। पिता की वर्तमान आयु ज्ञात कीजिए।
हल :
माना, पिता की वर्तमान आयु x वर्ष है तथा उसके दोनों बच्चों की वर्तमान आयु का योग y वर्ष है।
प्रश्नानुसार,
x = 3y …………….(i)
पाँच वर्ष बाद, पिता की आयु = x + 5
पाँच वर्ष बाद पुत्रों की आयु = (y + 5 + 5)
प्रश्नानुसर,
x + 5 = 2 (y + 5 + 5)
x + 5 = 2 ( y + 10 ) …………(ii)
x = 3y, समीकरण (ii) में रखने पर,
3y + 5 = 2y + 20
y = 15 वर्ष
अब, y = 15 समीकरण (i) में रखने पर,
x = 3 × 15
x = 45 वर्ष
अतः पिता की वर्तमान आयु 45 वर्ष है।

प्रश्न 12.
एक भिन्न \(\frac{1}{3}\) हो जाती है, अब उसके अंश से 2 घटाया जाता है, और \(\frac{1}{2}\) वह हो जाती है, जब हर में से 1 घटाया जाए। वह भिन्न ज्ञात कीजिए।
हल :
मान कि भिन्न \(\frac{x}{y}\) है
प्रश्नानुसार, \(\frac{x-2}{y}\) = \(\frac{1}{3}\) …………(i)
तथा \(\frac{x}{y-1}\) = \(\frac{1}{2}\)
⇒ 2x = y – 1
⇒ 2x + 1 = y …………(ii)
समीकरण (i) में y = 2x + 1, रखने पर,
\(\frac{x-2}{2 x+1}=\frac{1}{3}\)
3x – 6 = 2x + 1
x = 7
अब, समीकरण (ii) में x = 7 रखने पर,
y = 2 × 7 + 1
y = 15
अतः अभीष्ट भिन्न \(\frac{7}{15}\) है।

प्रश्न 13.
5 पेंसिलों तथा 7 पेनों का कुल मूल्य ₹ 250 है जबकि 7 पेंसिलों तथा 5 पेनों का कुल मूल्य ₹ 302 है। एक पेंसिल तथा एक पेन का मूल्य ज्ञात कीजिए।
हल :
माना एक पेंसिल का मूल्य ₹ तथा एक पेन का मूल्य ₹ y है।
प्रश्नानुसार,
5x + 7y = 250 ……..(1)
7x + 5y = 302 ………(2)
समीकरण (1) को 5 से तथा समीकरण (2) को 7 से गुणा करने पर
25x + 35y = 1250 ……..(3)
49x + 35y = 2114 ……..(4)
समीकरण (4) में समीकरण (3) घटाने पर

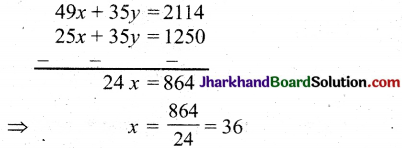
समीकरण (1) में x = 36 रखने पर,
5 × 36 + 7y = 250
7y = 250 – 180
y = \(\frac{70}{7}\) = 10
अत: एक पेंसिल का मूल्य = ₹ 36
तथा एक पेन का मूल्य = ₹ 10

प्रश्न 14.
निम्नलिखित समीकरण युग्म को व्रज-गुणन विधि से हल कीजिए:
x – 3y – 7 = 0
3x – 5y – 15 = 0
हल :
दिया गया समीकरण युग्म
x – 3y – 7 = 0
3x – 5y – 15 = 0
व्रज गुणन विधि से,

तथा \(\frac{y}{-6}=\frac{1}{4}\) ⇒ y = \(\frac{-6}{4}=\frac{-3}{2}\)
अत: x = \(\frac{5}{2}\) और y = \(\frac{-3}{2}\)

प्रश्न 15.
दो संख्याओं का अन्तर 26 है तथा बड़ी संख्या, छोटी संख्या के तीन गुने से 4 अधिक है। संख्याएँ ज्ञात कीजिए।
हल :
माना दो संख्याएँ x और y हैं। यहाँ x > y है।
प्रश्नानुसार x – y = 26 ………(i)
तथा x = 3y +4 ………..(ii)
समीकरण (ii) x = 3y + 4 समीकरण (i) में रखने पर
3y + 4 – y = 26
⇒ 2y = 26 – 4
⇒ y = \(\frac{22}{2}\) = 11
समीकरण (i) में y = 11 रखने पर,
x – 11 = 26
⇒ x = 26 + 11 = 37
अत: संख्याएँ 37 और 11 हैं।

प्रश्न 16.
x और y के मान ज्ञात कीजिए :
\(\frac{2}{x}+\frac{3}{y}\) = 13
\(\frac{5}{x}-\frac{4}{y}\) = – 2
हल :
माना \(\frac{1}{x}\) = a तथा \(\frac{1}{y}\) = b, तब दिए गए समीकरण निम्न प्रकार से होगे :
2a + 3b = 13 …………(i)
5a – 4b = – 2 …………(ii)
समीकरण (i) को 4 से तथा (ii) को उसे गुणा करके जोड़ने पर,
8a + 12b = 52
15a – 12b = – 6
23a = 46
⇒ a = \(\frac{46}{23}\) = 2
समीकरण (i) में a = 2 रखने पर,
2 × 2 + 3b = 13
⇒ 3b = 13 – 4 = 9
⇒ b = \(\frac{9}{3}\) = 3
अब a = \(\frac{1}{x}\) ⇒ \(\frac{1}{x}\) = 2 ⇒ x = \(\frac{1}{2}\)
और b = \(\frac{1}{y}\) ⇒ \(\frac{1}{y}\) = 3 ⇒ y = \(\frac{1}{3}\)
अतः x = \(\frac{1}{2}\) तथा y = \(\frac{1}{3}\)

प्रश्न 17.
k के किन मानों (किस मान) के लिए निम्न समीकरणों के युग्म का एक अद्वितीय हल है :
x + 2y = 5 और 3x + ky + 15 = 0
हल :
दिया है, समीकरण युग्मः
x + 2y = 5
और 3x + ky + 15 = 0
दिए गए समीकरणों के युग्म की समीकरणों a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर,
a₁ = 1, b₁ = 2, c = – 5, a₂ = 3, b₂ = k, c₂ = 15
∵ दिए गए युग्म का एक अद्वितीय हल है,
∴ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
अर्थात् \(\frac{1}{3}\) ≠ \(\frac{2}{k}\)
k ≠ 6
अत: 6 के अतिरिक्त, k के प्रत्येक मान के लिए दिए हुए समीकरणों के युग्म का एक अद्वितीय हल होगा।

प्रश्न 18.
c का मान कीजिए, यदि समीकरण निकाय cx + 3y + (3 – c) = 0, 12x + cy – c = 0 के अपरिमित रूप से अनेक हल हैं।
हल :
दिए गए समीकरण हैं :
cx + 3y + (3 – c) = 0
तथा 12x + cy – c = 0
दिए गए समीकरण युग्म की समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर,
a₁ = c, b₁ = 3, c₁ = 3 – c
तथा a₂ = 12, b₂ = c, c₂ = – c
रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होने के लिए शर्त:

प्रश्न 19.
K का मान ज्ञात कीजिए यदि समीकरण निकाय 2x + 3y = 7, (k + 1) x + (2k – 1) y = 4k + 1 के अपरिमित रूप से अनेक हल हैं।
हल :
दिए गए समीकरणों का निकाय है:
2x + 3y = 7
तथा (k + 1) x + (2k – 1)y = 4k + 1
जहाँ, a₁ = 2, b₁ = 3, तथा c₁ = – 7
और a₂ = (k + 1), b₂ = (2k – 1) तथा c₂ = – (4k + 1)
रैखिक समीकरणों के युग्म के अपरिमित रूप में अनेक हल होने के लिए शर्त

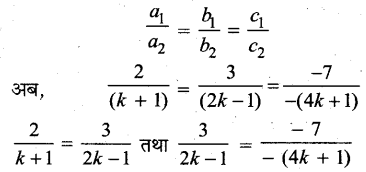
⇒ 4k – 2 = 3k + 3
4k – 3k = 3 + 2
k = 5
तथा 12k + 3 = 14k – 7
12k – 14k = – 7 – 3
– 2k = – 10
k = 5
अतः k = 5 है।

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. दो चरों वाले रैखिक समीकरण का आलेख सदैव एक ………………. रेखा को निरूपित करता है।
2. वह समीकरण युग्म जिसका हल अद्वितीय होता है, रैखिक समीकरणों का ………….. युग्म कहलाता है।
3. वह समीकरण युग्म जिसका कोई हल नहीं है, रैखिक समीकरणों का ………………… युग्म कहलाता है।
4. k का वह मान जिसके लिए समीकरण निकाय x + 2y = 3 तथा 5x + ky = 7 का कोई हल नहीं है, है ……………..
5. ………………… विधि में दोनों समीकरणों के दो चरों में से एक चर के गुणांक के समान करके विलुप्त कर दूसरे चर का मान ज्ञात करते हैं।

हल :

1. सरल,
2. संगत,
3. असंगत,
4. 10 या ± \(\frac{14}{3}\)
5. विलोपन

निम्न कथनों में सत्य / असत्य बताइए :

प्रश्न (ख)

1. दो चरों वाले रैखिक समीकरण का आलेख सदैव एक सरल रेखा को निरूपित करता है।
2. x और y के मानों से सम्बद्ध कोई भी युग्म जो दोनों समीकरणों को सन्तुष्ट करता हो, युग्म का शून्यक कहलाता है।
3. प्रतिच्छेदी रेखाओं के अनन्त हल होते हैं।
4. संपाती रेखाओं का केवल एक हल होता है।
5. समांतर रेखाओं का निकाय असंगत होता है।

हल :

1. सत्य,
2. सत्य,
3. असत्य,
4. असत्य,
5. सत्य

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
k का वह मान जिसके लिए समीकरण निकाय x + y – 4 = 0 तथा 2x + ky = 3 का कोई हल नहीं है, है:
(A) – 2
(B) ≠ 2
(C) 3
(D) 2
हल :
दिया है, निकाय का कोई हल नहीं है।

अत: सही विकल्प (D) है।

प्रश्न 2.
K का वह मान जिनके लिए रैखिक समीकरण युग्म kx + y = k² तथा x + ky = 1 के अपरिमित रूप से अनेक हल हैं, है:
(A) ± 1
(B) 1
(C) – 1
(D) 2
हल :
अपरिमित रूप से अनेक हल के लिए शर्त :

अतः सही विकल्प (A) है।

प्रश्न 3.
k का वहमान जिसके लिए रैखिक समीकरण निकाय x + 2y = 3, 5x + ky + 7 = 0 असंगत है, है :
(A) \(\frac{-14}{3}\)
(B) \(\frac{2}{5}\)
(C) 5
(D) 10
हल :
रैखिक समीकरण निकाय के लिए अंसगत होने के लिए शर्त्त :

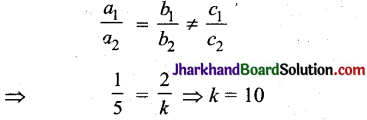
अत: सही विकल्प (D) है।

प्रश्न 4.
रैखिक समीकरणों y = 0 तथा y = – 6 के युग्म का एक:
(A) अद्वितीय हल है
(B) कोई हल नहीं है
(C) अनेक हल हैं
(D) सिर्फ एक हल (0, 0) है
हल :
सही विकल्प (B) है।

प्रश्न 5.
रैखिक समीकरणों \(\frac{3 x}{2}+\frac{5 y}{3}\) = 7 तथा 9x + 10y = 10 का युग्म :
(A) संगत है
(B) असंगत है
(C) संगत है तथा सिर्फ एक हल है।
(D) संगत है तथा अनेक हल हैं
हल :

अतः सही विकल्प (B) है।

प्रश्न 6.
k का मान जिसके लिए समीकरण 3x – y + 8 = 0 तथा 6x + ky = – 16 संपाती रेखाओं को व्यक्त करें, है:
(A) –\(\frac{1}{2}\)
(B) \(\frac{1}{2}\)
(C) 2
(D) – 2
हल :
∵ संपाती रेखाओं के लिए शर्त :

अत: सही विकल्प (D) है।

प्रश्न 7.
यदि रैखिक समीकरणों का कोई युग्म संगत हो, तो इसके आलेख की रेखाएँ होंगी :
(A) समांतर
(B) सदैव संपाती
(C) प्रतिच्छेदी या संपाती
(D) सदैव प्रतिच्छेदी
हल :
सही विकल्प (C) है।

प्रश्न 8.
समीकरण x = a और y = b का युग्म आलेखीय रूप से वे रेखाएँ निरूपित करता है, जो :
(A) समांतर हैं-
(B) (b, a) पर प्रतिच्छेद करती हैं।
(C) संपाती हैं
(D) (a, b) पर प्रतिच्छेद करती हैं
हल :
सही विकल्प (D) हैं।

प्रश्न 9.
आश्रित रैखिक समीकरणों के युग्म का एक समीकरण – 5x + 7 = 2 है। दूसरा समीकरण हो सकता है –
(A) 10x + 14y + 4 = 0
(B) – 10x – 14y + 4 = 0
(C) – 10x + 14y + 4 = 0
(D) 10x – 14y = – 4
हल :
सही विकल्प (D) है।

प्रश्न 10.
मेरी आयु पुत्र की आयु की तिगुनी है। 13 वर्ष बाद मेरी आयु पुत्र की आयु की दुगुनी रह जाएगी। मेरी और मेरे पुत्र की आयु बताइए-
(A) 39 वर्ष, 13 वर्ष
(B) 45 वर्ष, 15 वर्ष
(C) 30 वर्ष, 10 वर्ष
(D) 36 वर्ष, 12 वर्ष ।
हल :
मान लीजिए मेरी आयु (वर्षो में) x और मेरे पुत्र की आयु (वर्षो में) y है ।
प्रश्नानुसार, x = 3y ⇒ x – 3y = 0 … (i)
और x + 13 = 2(y + 13)
अर्थात् x – 2y = 26 – 13
⇒ x – 2y – 13 = 0
वज्रगुणन द्वारा समी. (i) व (ii) को हल करने पर

अर्थात् मेरी आयु 39 वर्ष और मेरे पुत्र की आयु 13 वर्ष है।
अत: सही विकल्प (A) है।

प्रश्न 11.
दो अंकों वाली संख्या के अंकों का योगफल 7 है। अंकों का क्रम उलट देने पर प्राप्त संख्या पहली संख्या से 9 अधिक है। वह संख्या ज्ञात कीजिए :
(A) 43
(B) 34
(C) 52
(D) 25
हल :
मान लीजिए दी हुई संख्या में दहाई अंक x और इकाई अंक y है। तब
दी हुई संख्या = 10x + y
अंकों का क्रम उलटने पर संख्या = 10y + x
प्रश्नानुसार, x + y = 7 ⇒ x + y – 7 = 0 ………….(i)
और (10x + y) + 9 = 10y + x
और 9x – 9y + 9 = 0
या x – y + 1 = 0 ……(ii)
समी. (i) व (ii) को वज्रगुणन द्वारा हल करने पर,

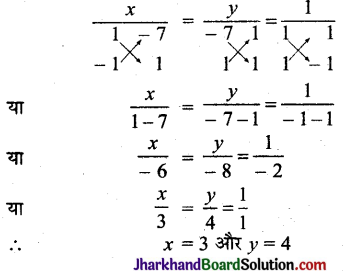
अतः अभीष्ट संख्या = 10x + y = 10 × 3 + 4 = 30 + 4 = 34 है।
सही विकल्प (B) है।

प्रश्न 12.
एक लड़के की आयु अभी अपनी माता की आयु की एक तिहाई है। यदि माता की वर्तमान आयु x वर्ष है तो 12 वर्ष बाद लड़के की आयु होगी :
(A) \(\frac{x}{3}\) + 12
(B) \(\frac{x+12}{3}\)
(C) x + 4
(D) \(\frac{x}{3}\) – 12
हल :
यहाँ माता की वर्तमान आयु = x वर्ष
माना पुत्र की वर्तमान आयु = y वर्ष
लेकिन प्रश्नानुसार, y = x × \(\frac{1}{3}\)
y = \(\frac{x}{3}\)
पुत्र की 12 वर्ष पश्चात् आयु = (y + 12) वर्ष
y = \(\frac{x}{3}\) रखने पर
अतः 12 वर्ष बाद लड़के की आयु = \(\frac{x}{3}\) + 12
सही विकल्प (A) है।

प्रश्न 13.
C के किस मान के लिए समीकरण युग्म Cx – y = 2 तथा 6x – 2y = 3 के अनन्त हल हैं:
(A) 3
(B) – 3
(C) – 12
(D) कोई मान नहीं
हल :
समीकरण युग्म को निम्न प्रकार लिखा जा सकता है :
Cx – y – 2 = 0 ……………(i)
तथा 6x – 2y – 3 = 0 ……………(ii)
समीकरण युग्म के अनन्त हल के लिए प्रतिबन्ध

अत: विकल्प (D) सही है।

प्रश्न 14.
k के किस मान के लिए समीकरण युग्म 4x – 3y = 9, 2x + ky = 11 का कोई हल नहीं है-
(A) \(\frac{9}{11}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{-3}{2}\)
(D) \(\frac{-2}{3}\)
हल :
दिया गया समीकरण युग्म है :
4x – 3y – 9 = 0, 2x + ky – 11 = 0
कोई हल न होने के लिए प्रतिबन्ध

⇒ k = \(\frac{-3}{2}\) या k ≠ \(\frac{-11}{3}\)
अतः k = \(\frac{-3}{2}\)
अत: सही विकल्प (C) है।

प्रश्न 15.
यदि समीकरणों 5x + 2y = 16 और 3x + \(\frac{6}{5}\)y = 2 का हल होगा :
(A) संगत
(B) असंगत
(C) दोनों (A) और (B)
(D) इनमें से कोई नहीं।
हल :
दिए गए समीकरण युग्म की निम्न प्रकार से भी लिख सकते हैं-
5x + 2y – 16 = 0 ……….(i)
15x + 6y – 10 = 0 ……….(ii)

अतः दिए गए समीकरण युग्म का कोई हल नहीं है। दिया गया समीकरण युग्म असंगत है ।
सही विकल्प (B) है।