Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution :
(i) We know that, cosec²A = 1 + cot² A ⇒ cosec A = \(\sqrt{1+\cot ^2 \mathrm{~A}}\)
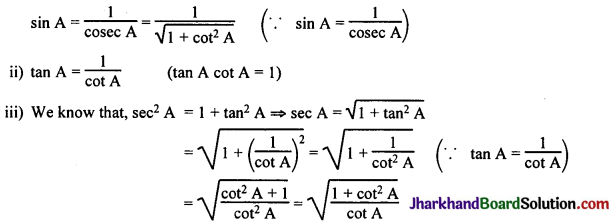
![]()
Question 2.
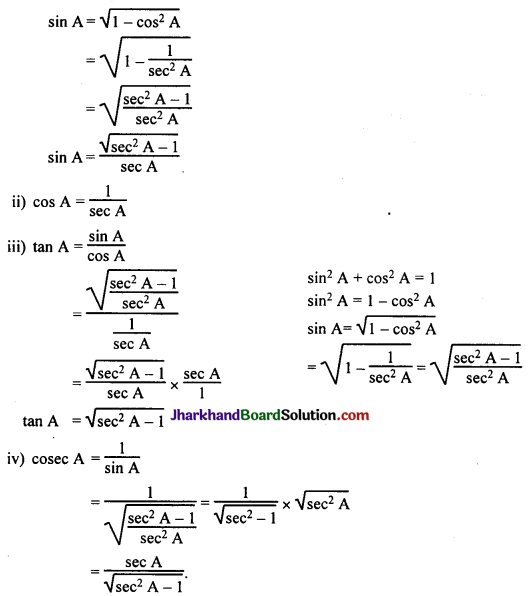
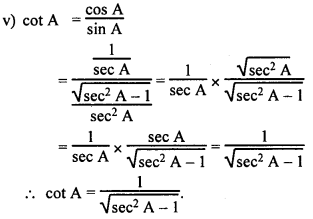
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution :
(i) sin A sin² A + cos² A = 1
sin² A = 1 – cos² A
Question 3.
Evaluate:
(i) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°.
Solution :
(i) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
sin (90 – θ) = cos θ
sin (90 – 27°) = cos 27°
sin 63° = cos 27°
sin² 63 = cos² 27°
cos (90 – θ) = sin θ
cos (90° – 73°) = sin 73°
cos (17°) = sin 73°
cos² 17° = sin² 73°
(ii) sin 25° cos 65° + cos 25° sin 65°
sin (90° – θ) = cos θ
sin (90° – 25°) = cos 25°
sin (90° – 65°) = cos 65°
sin 25° = cos 65°
cos (90° – θ) = sin θ
cos (90° – 65°) = sin 65°
cos 25° = sin 65°
sin 25° = cos 65°
cos 65° . cos 65° + sin 65° . sin 65°
∴ cos² 65 + sin² 65 = 1
![]()
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec² A – 9 tan² A=
(A) 1
(B) 9
(C) 8
(D) 0
Solution :
9 sec² A – 9 tan² A
9(1 + tan² A) – 9 tan² A
9 + 9 tan² A – 9 tan² A = 9.
∴ 9 sec² A – 9 tan² A = 9.
(ii) (1 + tan θ + sec θ) (1 + cot 0 – cosec θ) =
(A) 0
(B) 1
(C) 2
(D) – 1
Solution :

(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
Solution :
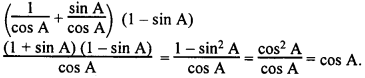
(iv) \(\frac{1+\tan ^2 A}{1+\cot ^2 A}\) =
(A) sec² A
(B) – 1
(C) cot² A
(D) tan² A
Solution :
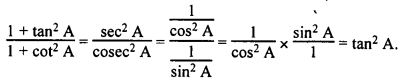
Question 5.
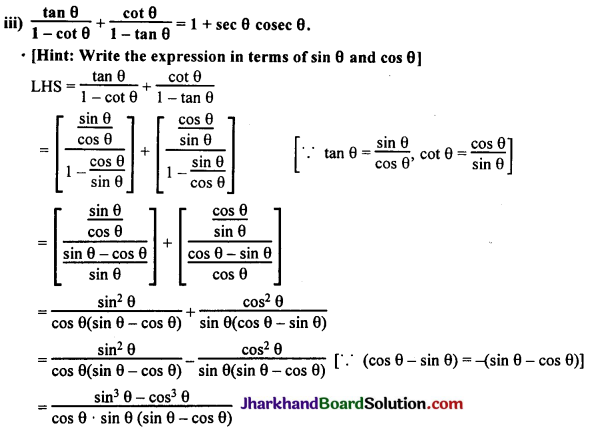
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Solution :





(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.
LHS = sin² A + cosec² A + 2 sin A cosec A + cos² A + sec² A + 2 cos A sec A [∵ (a + b)² = a² + b² + 2ab]
= (sin² A + cos² A) + (1 + cot² A) + 2 sin A . \(\frac{1}{sin A}\) + (1 + tan² A) + 2 cos A . \(\frac{1}{cos A}\) (∵ 1 + cot² A = cosec² A and sec² A = 1 + tan² A)
= 1 + 1 + cot² A + 2 + 1 + tan² A + 2 (∵ sin² A + cos² A = 1)
= 7 + tan² A + cot² A = RHS.
(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
Solution :
[Hint: Simplify LHS and RHS separately].
LHS = (cosec A – sin A) (sec A – cos A)
