JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 Constructions Exercise 11.1

In each of the following, give the justification of the construction also:

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution :

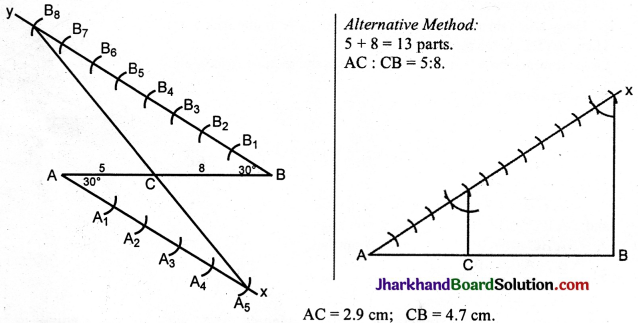
Steps of construction:
1. Draw the line segment AB = 7.6 cm.
2. At A, below AB, make an angle BAx = 30°.
3. At B, above AB, make an angle ABy = 30°.
B\(\hat{A}\)x = A\(\hat{B}\)y = 30°
These are alternate angles. ∴ Ax || By.
4. With a convenient radius cut off five equal parts
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ in Ax.
5. With the same radius cut off eight equal parts.
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈.
6. Join A₅B₈. Let it cut AB at C.
AC : CB = 5 : 8.

In ΔACA₅ and CBB₈
1. A\(\hat{C}\)A₅ = B\(\hat{C}\)B₈ (V.O.A.)
2. C\(\hat{A}\)A₅ = A\(\hat{B}\)B₈ (Alternate angles)
3. C\(\hat{A}\)₅A = B\(\hat{B}\)₈C (Alternate angles)
Δs are equiangular.
∴\(\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{\mathrm{CA}_5}{\mathrm{AB}_8}=\frac{\mathrm{CA}}{\mathrm{BC}}\)
∴ \(\frac{\mathrm{CA}}{\mathrm{BC}}=\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{5}{8}\)

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.
Solution :

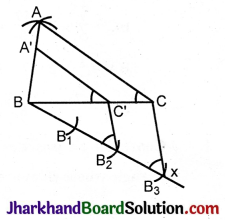
Steps of construction:

1. Construct ΔABC given AB = 4 cm, BC = 5 cm, AC = cm.
2. At B, make an acute angle CBx.
3. Divide Bx into three equal parts with a convenient radius.
4. Join B₃C.
5. From B₂ draw a parallel to B₃C.
6. Let it cut BC at C’.
7. At C’ make angle A’C’B = ACB.

Join A’C’.
∴ ΔABC ||| A’BC’.

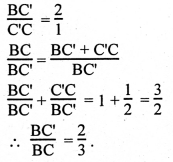
In ΔABC and ΔA’BC’,
1.A\(\hat{B}\)C = A’\(\hat{B}\)C’ (Common angle)
2. A\(\hat{C}\)B = A’\(\hat{C’}\)B (Corresponding angles)
3. B\(\hat{A}\)C = B\(\hat{A’}\)C’ (Remaining angles)
Δs are equiangular.
∴ \(\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{BC} \mathrm{C}^{\prime}}\) = \(\frac{3}{2}\) ∴ [latex]\frac{BC’}{BC}=\frac{2}{3}[/latex]

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac{7}{5}\) of the corresponding sides of the first triangle.
Solution :
Steps of construction:

1. Construct a triangle ABC given BC= 7 cm, AB = 5 cm, AC = 6 cm.
2. At B, below BC, make an acute angle CBx.
3. With a convenient radius cut off seven equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
4. Join B₅C.
5. From B₁ draw a parallel to B₅C to cut BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

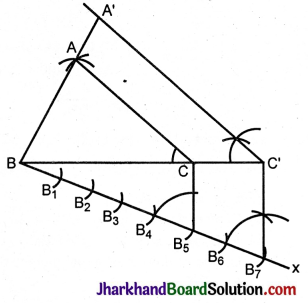
A’BC’ is the required triangle.
In ΔABC and ΔA’BC’

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution :

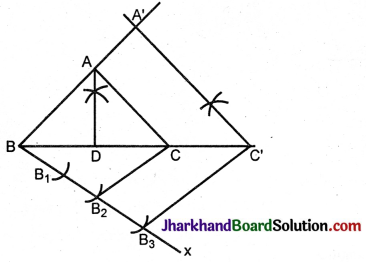
Steps of construction:

1. Draw a line segment BC = 8 cm.
2. Draw its perpendicular bisector.
3. Cut off DA = 4 cm. (altitude given)
4. Join AB and AC. ABC is the required triangle.
5. At B, below BC, draw an acute angle CBx.
6. With a convenient radius cut off three equal parts BB₁ = B₁B₂ = B₂B₃.
7. Join B₂C.
8. At B₃ draw a parallel to B₂C to meet BC extended at C’.
9. At C’ draw a parallel to CA to meet BA produced at A’.
10. Join A’C’. A’BC’ is the required triangle similar to ΔABC.

In ΔA’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C (Common angle)
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. A’\(\hat{C}\)‘B = A\(\hat{C}\)B
Δs are equiangular.
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}\)
\(\frac{BC’}{BC}\) = \(\frac{3}{2}\)
BC = 8 cm, BC’ = 8 × \(\frac{3}{2}\) = 12 cm.
BA = CA = 5.6 cm ∴ A’B = A’C’ = 5.6 × \(\frac{3}{2}\) = 8.4 cm.

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of the triangle ABC.
Solution :

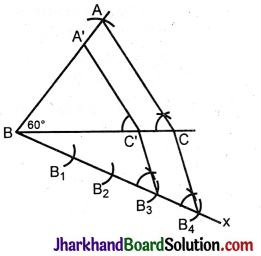
Steps of construction:

1. Construct ΔABC given BC = 6 cm, AB = 5 cm, A\(\hat{B}\)C = 60°.
2. At B, below BC, make an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. Join B₄C.
5. From B₃ draw a parallel to B₄C to meet BC at C’.
6. At C’ draw a parallel to CA to meet CA at A’.

A’BC’ is the required triangle similar to ΔABC.
In Δs A’BC’ and ABC

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{4}{3}\) times the corresponding sides of ΔABC.
Solution :

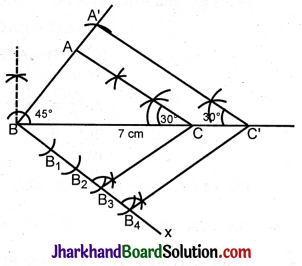
\(\hat{A}\) + \(\hat{B}\) + \(\hat{C}\) = 180°
\(\hat{A}\) + \(\hat{B}\) = 150° (105° + 45°)
∴ \(\hat{C}\) = 30°
Steps of construction:
1. In ΔABC, BC = 7 cm.
\(\hat{B}\) = 45°, \(\hat{C}\) = 105°
∴ \(\hat{A}\) = 180° – 45° – 105°
= 180° – 150° = 30°.
Construct ΔABC given BC = 7 cm, \(\hat{B}\) = 45°, \(\hat{C}\) = 30°.
2. At B draw an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ with a convenient radius.
4. Join B₃C.
5. At B₄ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ make angle of 30° equal to A\(\hat{C}\)B. Let it meet BA produced at A’.
A’BC’ is the required triangle similar to ΔABC.
In ΔC’BB₄ CB₃ || C’B₄

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution :

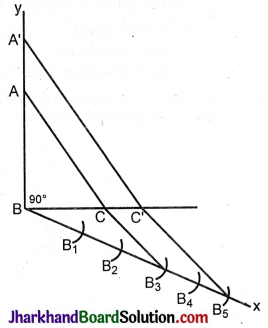
BC’ = \(\frac{5}{3}\) × BC = \(\frac{5}{3}\) × 3 = 5 cm
BA’= \(\frac{5}{3}\) × 4 = \(\frac{20}{3}\) = 6.6 cm
A’C’ = \(\frac{5}{3}\) × 5 = \(\frac{25}{3}\) = 8.3 cm.

Steps of construction:

1. Construct ΔABC given BC= 3 cm, \(\hat{B}\) = 90°, BA = 4 cm.
2. At B, make an acute angle CBx.
3. Cut off five equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ along Bx with a convenient radius.
4. Join B₃C.
5. At B₅ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

A’BC’ is the required triangle similar to ΔABC.
BC’ : BC = BB₅ = BB₃
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_5}{\mathrm{BB}_3}\) = \(\frac{5}{3}\)

In Δs A’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C = 90°
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. B\(\hat{C}\)‘A’ = B\(\hat{C}\)A
Δs are equiangular.
∴ \(\frac{A’C’}{AC}\) = \(\frac{BC’}{BC}\) = \(\frac{BA’}{BA}\) = \(\frac{5}{3}\)