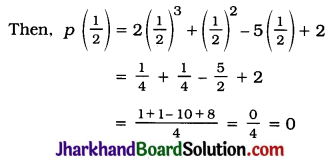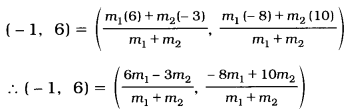Month: March 2023

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1

Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting ?) Represent this situation algebraically and graphically.
Solution:
Let the present age of Aftab be x years and the present age of his daughter be y years. Then, seven years ago, the age of Aftab was x – 7 years and the age of his daughter was y – 7 years.
So, from the given data.
x – 7 = 7(y – 7)
∴ x – 7 = 7y – 49
x – 7y + 42 = 0 …….. (1)
Similarly, three years from now, the age of Aftab will be x + 3 years and the age of his daughter will be y + 3 year.
So, according to the given data,
x + 3 = 3(y + 3)
∴ x + 3 = 3y + 9
∴ x – 3y – 6 = 0 ….. (2)
Thus, the equations x – 7y + 42 = 0 and x – 3y – 6 = 0 represent the given situation algebraically.
To represent the given situation graphically. we draw the graphs of both the equations.
x – 7y + 42 = 0
∴ y = \(\frac{42+x}{7}\)

x	0	35
y	6	11

x – 3y – 6 = 0
∴ y = \(\frac{x-6}{3}\)

x	0	30
y	-2	8

The above graph represents the situation graphically.
We observe that the lines intersect at point (42, 12).

Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let the cost of one bat be ₹ x and the cost of one ball be ₹ y.
Then, the total cost of 3 bats is ₹ 3x and that of 6 balls is ₹ 6y. From the data, the total cost is ₹ 3900.
∴ 3x + 6y = 3900
∴ x + 2y = 1300
Similarly, the cost of 1 bat is ₹ x and the total cost of 3 balls is ₹ 3y. From the data, the total cost is ₹ 1300.
∴ x + 3y = 1300
Thus, the equations x + 2y = 1300 and x + 3y = 1300 represent the given situation algebraically.
To represent the given situation geometrically. we draw the graphs of both the equations.
x + 2y = 1300

x	100	1300
y	600	0

x + 3y = 1300

x	100	1300
y	400	0

The above graph represents the situation geometrically.
We observe that the lines intersect at point (1300, 0).

Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be After a month, the cost of 4 kg of apples and 2 kg of grapes is 300. Represent the situation algebraically and geometrically.
Solution:
Let the cost of 1 kg of apples be ₹ x and the cost of 1 kg of grapes be ₹ y.
Then, from the given data, 2x + y = 160 and 4x + 2y = 300.
Thus, the equations 2x + y = 160 and 4x + 2y = 300 represent the given situation algebraically.
To represent the given situation geometrically. we draw the graphs of both the equations.
2x + y = 160

x	0	80
y	160	0

4x + 2y = 300

x	0	75
y	150	0

The above graph represents the situation geometrically.
We observe that the lines are parallel.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.2

Question 1.
In the given figures (1) and (2), DE || BC. Find EC in (1) and AD in (2).
Answer:

1. Line DE is parallel to side BC of AABC and it intersects AB and AC at D and E respectively.
∴ \(\frac{AD}{DB}=\frac{AE}{EC}\) (Theorem 6.1)
∴ \(\frac{1.5}{3}=\frac{1}{EC}\)
∴ EC = \(\frac{1 \times 3}{1.5}\)
∴ EC = 2cm

2. Line DE is parallel to side BC of ΔABC and it intersects AB and AC at D and E respectively.
∴ \(\frac{AD}{DB}=\frac{AE}{EC}\) (Theorem 6.1)
∴ \(\frac{AD}{7.2}=\frac{1.8}{5.4}\)
∴ AD = \(\frac{1.8 \times 7.2}{5.4}\)
∴ AD = 2.4 cm

Question 2.
E and F are points on the sides PQ and PR respectively of a PQR. For each of the following cases, state whether EF || QR
1. PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
2. PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
3. Pg = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
E and F are points on the sides PQ and PR respectively of ΔPQR.

1. Here, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3}=\frac{1.3}{1}\) and
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{2.4}=\frac{1.5}{1}\)
So, \(\frac{PE}{EQ}\) = \(\frac{PF}{FR}\)
Hence, by the converse of BPT, EF is not parallel to QR.

2. Here, \(\frac{\mathrm{PE}}{\mathrm{QE}}=\frac{4}{4.5}=\frac{8}{9}\) and \(\frac{PF}{RF}\) = \(\frac{8}{9}\)
So, \(\frac{PE}{QE}\) = \(\frac{PF}{RF}\)
Hence, by the converse of BPT, EF || QR.

3. Here, \(\frac{\mathrm{PE}}{\mathrm{PQ}}=\frac{0.18}{1.28}=\frac{9}{64}\) and
\(\frac{PF}{PR}=\frac{0.36}{2.56}=\frac{9}{64}\)
So, \(\frac{PE}{PQ}\) = \(\frac{PF}{PR}\)
Hence, by theorem 6.2, EF || QR.

Question 3.
In the given figure, if LM || CB and LN || CD, prove that \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\)
Answer:

In ΔABC, LM || CB and LM intersects AB and AC at M and L respectively.
∴ \(\frac{AM}{AB}=\frac{AL}{AC}\)(BPT) ……….(1)
In ΔACD, LN || CD and LN intersects AC and AD at L and N respectively.
∴ \(\frac{AL}{AC}=\frac{AN}{AD}\)(BPT) ……….(2)
From (1) and (2), \(\frac{AM}{AB}=\frac{AN}{AD}\)

Question 4.
In the given figure, DE || AC and DF || AE.
Prove that \(\frac{AM}{AB}\) = \(\frac{AN}{AD}\)
Answer:

In ΔABE, DF || AE and DF intersects AB and BE at D and F respectively.
∴ \(\frac{BF}{FE}=\frac{BD}{DA}\) (BPT) …………(1)
In ΔABC, DE || AC and DE intersects BA and BC at D and E respectively.
∴ \(\frac{BD}{DA}=\frac{BE}{EC}\) …………(2)
From (1) and (2), \(\frac{BF}{FE}=\frac{BE}{EC}\)

Question 5.
In the given figure, DE || OQ and DF || OR. Show that EF || QR.
Answer:

In ΔPQO, DE || OQ
∴ \(\frac{PE}{EQ}=\frac{PD}{DO}\) (BPT) …………(1)
In ΔPOR, DF || OR
∴ \(\frac{PD}{DO}=\frac{PF}{FR}\) (BPT) …………(2)
From (1) and (2), \(\frac{PE}{EQ}=\frac{PF}{FR}\)
Now, line EF intersects sides PQ and PR of ΔPQR at E and F respectively and \(\frac{PE}{EQ}=\frac{PF}{FR}\)
Hence, by converse of BPT, EF || QR.

Question 6.
In the given figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
Answer:

In ΔOPQ, AB || PQ and AB intersects OP and OQ at A and B respectively.
∴ \(\frac{OA}{AP}=\frac{OB}{BQ}\) (BPT) …………(1)
In ΔOPR, AC || PR and AC intersects OP and OR at A and C respectively.
∴ \(\frac{OA}{AP}=\frac{OC}{CR}\) (BPT) …………(2)
From (1) and (2), \(\frac{OB}{BQ}=\frac{OC}{CR}\)
In ΔOQR, BC intersects OQ and OR at B and C respectively such that \(\frac{OB}{BQ}=\frac{OC}{CR}\)
∴ BC || QR (Converse of BPT)

Question 7.
Using theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Given:
In ΔABC, P is the mid-point of side AB. Through P a line is drawn parallel to BC to intersect AC at Q.
To prove : Q is the mid-point of AC.

Proof: In ΔABC, P and Q lie on AB and AC respectively such that PQ || BC.
∴ \(\frac{AP}{PB}=\frac{AQ}{QC}\) (Theorem 6.1) ………(1)
Now, P is the mid-point of AB.
∴ AP = PB
∴ \(\frac{AP}{PB}\) = 1 ………(2)
From (1) and (2).
\(\frac{AP}{PB}\) = 1
∴ AQ = QC
∴ Q is the mid-point of AC.
Note: In Class IX, this was proved with the help of properties of a parallelogram.

Question 8.
Using theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Answer:
Given: In ΔABC, P and Q are the mid-points of AB and AC respectively.
To prove : PQ || BC

Proof: Here, P is the mid-point of AB.
∴ AP = PB
∴ \(\frac{AP}{PB}\) = 1 ……………(1)
Q is the mid-point of AC.
∴ AQ = QC
∴ \(\frac{AQ}{QC}\) = 1 ……………(2)
So, by (1) and (2).
\(\frac{AP}{PB}=\frac{AQ}{QC}\)
Now, in ΔABC, points P and Q lie on AB and AC respectively and \(\frac{AP}{PB}=\frac{AQ}{QC}\)
∴ By theorem 6.2. PQ || BC.

Question 9.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{AO}{BO}=\frac{CO}{DO}\)
Answer:
Given: ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O.
To prove : \(\frac{AO}{BO}=\frac{CO}{DO}\)

Construction: Through O draw a line parallel to AB which intersects AD at P.
Proof: Here, OP || AB and AB || DC.
∴ OP || DC.
In ΔADC, OP || DC and points P and O lie on AD and AC respectively.
∴ \(\frac{OA}{OC}=\frac{PA}{PD}\) (Theorem 6.1) …………….(1)
In ΔDAB, OP || AB and points P and O lie on AD and BD respectively.
∴ \(\frac{PA}{PD}=\frac{OB}{OD}\) (Theorem 6.1) …………….(2)
From (1) and (2), we get
\(\frac{OA}{OC}=\frac{OB}{OD}\)
∴ \(\frac{OA}{OB}=\frac{OC}{OD}\)
∴ \(\frac{AO}{BO}=\frac{CO}{DO}\)

Question 10.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{AO}{BO}=\frac{CO}{DO}\). Show that ABCD is a trapezium.
Answer:
Given: In quadrilateral ABCD, diagonals AC and BD intersect at O such that \(\frac{AO}{BO}=\frac{CO}{DO}\)
To prove : ABCD is a trapezium.

Construction: Through O draw a line parallel to AB to intersect AD at P.
Proof: Here, in ΔDAB, points P and O lie on DA and DB respectively and PO || AB.
∴ \(\frac{AP}{DP}=\frac{BO}{DO}\) (Theorem 6.1) ………….(1)
Now, \(\frac{AO}{BO}=\frac{CO}{DO}\) (Given)
∴ \(\frac{AO}{CO}=\frac{BO}{DO}\) ………….(2)
From (1) and (2),
\(\frac{AP}{DP}=\frac{AO}{CO}\)
Now, in ΔADC, points P and O lie on AD and AC respectively and \(\frac{AP}{DP}=\frac{AO}{CO}\)
∴ By theorem 6.2. PO || DC.
Now, PO || AB (By construction) and PO || DC (Proved).
Hence, AB || DC
Thus, in quadrilateral ABCD, AB || DC.
Hence, ABCD is a trapezium.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 6 Triangles Ex 6.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 6 Triangles Exercise 6.1

Question 1.
Fill in the blanks using the correct word given in brackets:

1. All circles are …………… (congruent, similar)
2. All squares are ……….. (similar, congruent)
3. All ……………. triangles are similar. (isosceles, equilateral)
4. Two polygons of the same of sides are similar, if (a) their corresponding angles are …… and (b) their corresponding sides are ……….. (equal, proportional)

Answer:

1. similar
2. similar
3. equilateral
4. equal, proportional

Question 2.
Give two different examples of pair of
1. similar figures.
2. non-similar figures.
Answer:
1. Similar figures: Any two squares are similar. Any two equilateral triangles are similar. Any two circles are similar.
2. Non-similar figures: An equilateral triangle and an obtuse angled triangle are non- similar. An equilateral triangle and a right angled triangle are non-similar.

Question 3.
State whether the following quadrilaterals are similar or not:
Answer:

No, because for any correspondence between their vertices, the corresponding sides are proportional but the corresponding angles are not equal.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.4

Question 1.
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7).
Answer:
Let the line 2x + y – 4 = 0 divide the line segment joining the point A (2, – 2) and B (3, 7) at point M (a, b) in the ratio k : 1.
Then, the coordinates of point M are
(\(\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\)) = (a, b)
∴ a = \(\frac{3k+2}{k+1}\)
and b = \(\frac{7k-2}{k+1}\) …… (1)
Now, the point M also lies on line 2x + y – 4 = 0.
Hence, (a, b) must satisfy
2x + y – 4 = 0
∴ 2a + b – 4 = 0
∴ 2(\(\frac{3k+2}{k+1}\)) + (\(\frac{7k-2}{k+1}\)) – 4 = 0 [From (1)]
∴ 6k + 4 + 7k – 2 – 4k – 4 = 0
∴ 9k – 2 = 0
∴ k = \(\frac{2}{9}\)
Hence, the ratio k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9.
Thus, the line 2x + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7) in the ratio 2 : 9.

Question 2.
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Answer:
Points A (x, y), B(1, 2) and C(7,0) are collinear.
∴ Area of ΔABC = 0
∴ \(\frac{1}{2}\)[x(2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
∴ 2x – y + 7y – 14 = 0
∴ 2x + 6y – 14 = 0
∴ x + 3y – 7 = 0
Thus, x + 3y – 7 = 0 is the required relation between x and y.

Question 3.
Find the centre of the circle passing through the points (6, – 6), (3, – 7) and (3, 3).
Answer:
Let A (6, 6), B (3, 7) and C(3, 3) be the given points and P(x, y) be the centre of the circle passing through these points. Then, P is equidistant from all the points A, B and C.
∴ PA = PB = PC
∴ PA² = PB² = PC²
Now, PA² = PB² gives
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
∴ x² – 12x + 36 + y² + 12y +36 = x² – 6x + 9 + y² + 14y + 49
∴ – 6x – 2y = – 14
∴ 3x + y = 7 …………..(1)
Again, PA² = PC² gives
(x – 6)² + (y + 6)² = (x – 3)² + (y – 3)²
∴ x² – 12x + 36 + y² + 12y + 36 = x² – 6x + 9 + y² – 6y + 9
∴ – 6x + 18y = – 54
∴ x – 3y = 9 …………..(2)
Multiplying equation (1) by 3, we get
9x + 3y = 21
Adding equations (2) and (3), we get 10x = 30
10x = 3
∴ x = 3
Substituting x = 3 in 3x + y = 7, we get 9 + y = 7. i.e., y = – 2
∴ The coordinates of P are (3, – 2).
Thus, the centre of the circle passing through the given points is (3, – 2).

Question 4.
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.

Answer:
Let ABCD be the given square in which A(-1, 2) and C(3, 2) are given vertices and B and D are to be found.
Let the coordinates of B be (x, y).
In ΔABC, ∠B = 90° and AB = BC.
AB = BC
∴ AB² = BC²
∴ (x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²
∴ x² + 2x + 1 + y² – 4y + 4 = x² – 6x + 9 + y² – 4y + 4
∴ 8x = 8
∴ x = 1
In ΔABC,
∠B = 90°
Hence, by Pythagoras theorem,
AB² + BC² = AC²
∴ (x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
∴ x² + 2x + 1 + y² – 4y + 4 + x² – 6x + 9 + y² – 4y + 4 = 16
∴ 2x² – 4x + 2y² – 8y + 18 – 16 = 0
∴ 2(1)² – 4(1) + 2y² – 8y + 2 = 0 (Substituting x = 1)
∴ 2 – 4 + 2y² – 8y + 2 = 0
∴ 2y² – 8y = 0
∴ 2y (y – 4) = 0
∴ 2y = 0 or y – 4 = 0
∴ y = 0 or y = 4
These two values of y gives us the y-coordinates of B and D while the single value of x suggests that the x-coordinate of B and D is same. Thus, the coordinates of the other two vertices are (1, 0) and (1, 4) respectively.

Question 5.
The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the given figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

1. Taking A as origin, find the coordinates of the vertices of the triangle.
2. What will be the coordinates of the vertices of ΔPQR if C is the origin? Also calculate the areas of the triangles in these cases. What do you observe?
Answer:
1. Taking A as the origin and AB and AD as the y-axis and the x-axis respectively, we get the coordinates of points as A (0, 0), B(0, 8), D(16, 0) and C(16, 8).
Then, the vertices of ΔPQR are P (4, 6), 9 (3, 2) and R (6, 5).
Area of ΔPQR
= \(\frac{1}{2}\)[4(2 – 5) + 3(5 – 6) + 6(6 – 2)]
= \(\frac{1}{2}\)[- 12 – 3 + 24]
= \(\frac{9}{2}\) sq units

2. Taking C as the origin and CB and CD as positive x-axis and y-axis respectively, we get C(0, 0), B(16, 0), D (0, 8) and A (16, 8) as the vertices of quadrilateral ABCD. Then, the vertices of ΔPQR are P (12, 2), Q (13, 6) and R(10, 3).
Area of ΔPQR
= \(\frac{1}{2}\)[12(6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\)[36 + 13 – 40]
= \(\frac{9}{2}\)sq units
We observe that the area of ΔPQR is same in both the cases.
Note: In second case, if we take CB and CD as negative x-axis and y-axis, then the vertices of ΔPQR will be P(-12, -2), Q(-13,-6) and R(-10,-3). Still the area of ΔPQR would not change.

Question 6.
The vertices of a ΔABC are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}\). Calculate the area of the ΔADE and compare it with the area of ΔABC.
Answer:

Similarly, \(\frac{AE}{EC}=\frac{1}{3}\)
Now, D divides the join of A (4, 6) and B(1, 5) in the ratio 1:3.
Then the coordinates of D are

So, area of ΔADE : area of ΔABC = 1 : 16
Thus, the area of ΔADE is \(\frac{15}{32}\) sq units and the ratio of areas of ΔADE and ΔABC is 1 : 16.

Question 7.
Let A (4, 2), B (6, 5) and C(1, 4) be the vertices of AABC.
1. The median from A meets BC at D. Find the coordinates of the point D.
2. Find the coordinates of the point P on AD such that AP : PD = 2 : 1
3. Find the coordinates of points Q and R on medians BE and CF respectively such that BQ:QE=2:1 and CR : RF = 2:1.
4. What do you observe? [Note: The point which is common to all the three medians is called the centroid and this point divides each median in the ratio 2:1.]
5. If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) and the vertices of ΔABC, find the coordinates of the centroid of the triangle.

Answer:
1. AD is a median. Hence, D is the midpoint of BC.
Then, the coordinates of D, by midpoint formula, are (\(\frac{6+1}{2}, \frac{5+4}{2}\))
= (\(\frac{7}{2}\), \(\frac{9}{2}\)).

2. Point P divides AD in the ratio 2 : 1.
∴ Coordinates of P by section formula, are (\(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}, \frac{2\left(\frac{9}{2}\right)+2}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

3. BE is a median. Hence, E is the midpoint of AC.
Then, the coordinates of E, by midpoint formula, are
(\(\frac{4+1}{2}, \frac{2+4}{2}\)) = (\(\frac{5}{2}\), 3).
Now, Q divides BE in the ratio 2 : 1.
∴ Coordinates of Q, by section formula, are (\(\frac{2\left(\frac{5}{2}\right)+1(6)}{2+1}, \frac{2(3)+1(5)}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))
CF is a median, Hence, F is the midpoint of AB.
Then, the coordinates of F, by midpoint formula are (\(\frac{4+6}{2}, \frac{2+5}{2}\)) = (5, \(\frac{7}{2}\)).
Point R divide CF in the ratio 2 : 1.
∴ Coordinates of R, by section formula, are (\(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

4. Here, we observe that points P(\(\frac{11}{3}\), \(\frac{11}{3}\)), Q(\(\frac{11}{3}\), \(\frac{11}{3}\)) and R(\(\frac{11}{3}\), \(\frac{11}{3}\)) are the same points. i.e., P = Q = R.
This means that all the three medians are concurrent at point P (or Q or R).
This point is called the centroid of the triangle which is usually denoted by letter G. Centroid of a triangle divides each of its medians in the ratio 2 : 1 from the vertex side.

5. Now, the coordinates of the vertices of ΔABC are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃).
AD, BE and CF are medians.
Hence, D, E and F are the midpoints of BC, AC and AB respectively.

Note: Now, with this formula, we can verify the answers received in part (2) and (3), as (\(\frac{4+6+1}{3}, \frac{2+5+4}{3}\)) = (\(\frac{11}{3}\), \(\frac{11}{3}\))

Question 8.
ABCD is a rectangle formed by the points A(-1, -1), B(1, 4), C (5, 4) and D (5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Answer:

In rectangle ABCD, P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Then, the coordinates of P, Q, R and S are obtained as

So, in quadrilateral PQRS,
PQ² = QR² = RS² SP2 but PR² ≠ QS², i.e..
PQ = QR = RS = SP but PR ≠ QS
So, in quadrilateral PQRS, all the sides are equal but diagonals are not equal.
Hence, PQRS is a rhombus.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 Polynomials Exercise 2.4

Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
1. 2x³ + x² – 5x + 2; \(\frac{1}{2}\), 1, -2
2. x³ – 4x² + 5x – 2; 2, 1, 1
Solution:
1. Let p(x) = 2x³ + x² – 5x + 2

Hence, \(\frac{1}{2}\) is a zero of
p(x) = 2x³ + x² – 5x + 2.
Again,
p(1) = 2(1)³ + (1)² – 5(1) + 2
= 2 + 1 – 5 + 2 = 0
Hence, 1 is a zero of p(x) = 2x³ + x² – 5x + 2.
Again,
p(-2) = 2(-2)² + (-2)² – 5(-2)+2
= -16 + 4 + 10 + 2 = 0
Hence, -2 is a zero of
p(x) = 2x³ + x² – 5x + 2.
Now, for p(x) = 2x³ + x² – 5x + 2;
a = 2, b = 1, c = -5 and d = 2.
The zeroes of p (x) are α = \(\frac{1}{2}\), β = 1 and γ = -2.
Now, α + β + γ = \(\frac{1}{2}\) + 1 + (-2)
= \(-\frac{1}{2}=\frac{-(1)}{2}=\frac{-b}{a}\)
αβ + βγ + γα = (\(\frac{1}{2}\)) (1) + (1) (-2) + (-2) (\(\frac{1}{2}\))
= \(\frac{1}{2}\) – 2 – 1 = \(\frac{-5}{2}=\frac{c}{a}\) and
αβγ = (\(\frac{1}{2}\))(1)(-2) = -1 = \(\frac{-(2)}{(2)}=\frac{-d}{a}\)

2. Let p (x) = x³ – 4x² + 5x – 2.
Then, p (2) = (2)³ – 4(2)² + 5(2) – 2
= 8 – 16 + 10 – 2 = 0
Hence, 2 is a zero of p (x) = x³ – 4x² + 5x – 2.
Again,
p(1) = (1)³ – 4(1)² + 5(1) – 2
= 1 – 4 + 5 – 2 = 0
Hence, 1 is a repeated zero of p(x) = x³ – 4x² + 5x – 2.
Now, for p(x) = x³ – 4x² + 5x – 2, a = 1, b = -4, c = 5 and d = -2.
The zeroes of p (x) are α = 2, β = 1 and γ = 1.
Now,
α + β + γ = 2 + 1 + 1 = 4 = \(\frac{-(-4)}{1}=\frac{-b}{a}\)
αβ + βγ + γα = (2) (1) + (1) (1) + (1) (2)
= 2 + 1 + 2 = 5 = \(\frac{5}{1}=\frac{c}{a}\) and
αβγ = (2) (1) (1) = 2 = \(\frac{-(-2)}{1}=\frac{-d}{a}\)

Question 2.
Find a cubic polynomial with the sum of its zeroes, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, 7, 14 respectively.
Solution:
Let p (x) = ax³ + bx² + cx + d, a ≠ 0, be the required cubic polynomial and its zeroes be α, β and γ
Then, as given in the data,
α + β + γ = 2 ∴ \(\frac{-b}{a}\) = 2
αβ + βγ + γα = -7 ∴ \(\frac{c}{a}\) = -7
αβγ = \(\frac{-d}{a}\) = -14
So, if a = 1, then b = -2, c = -7 and d = 14.
Hence, the required polynomial is p(x) = x³ – 2x² – 7x + 14.

Question 3.
If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Solution:
For the given polynomial x³ – 3x² + x + 1.
A = 1, B = -3, C = 1 and D = 1.
Its zeroes are given to be a – b, a and a + b.
Now, sum of zeroes = (a – b) + a + (a + b) = 3a
From the polynomial,
Sum of zeroes = \(\frac{-B}{A}=\frac{-(-3)}{1}=3\)
Hence, 3a = 3 ∴ a = 1
Product of zeroes = (a – b) × a × (a + b)
= a(a² – b²)
From the polynomial.
Product of zeroes = \(\frac{-\mathrm{D}}{\mathrm{A}}=\frac{-1}{1}=-1\)
Hence, a (a² – b²) = -1
1(1² – b²) = -1 ∴ 1 – b² = -1
∴ 1 + 1 = b² ∴ b² = 2
∴ b = ±\(\sqrt{2}\)
Thus, a = 1 and b = ±\(\sqrt{2}\).

Question 4.
It two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2±\(\sqrt{3}\), find other zeroes.
Solution:
Let p (x) = x⁴ – 6x³ – 26x² + 138x – 35
2 + \(\sqrt{3}\) and 2 – \(\sqrt{3}\) are zeroes of p (x).
∴ (x – 2 – \(\sqrt{3}\))(x – 2 + \(\sqrt{3}\)) = (x – 2)² – (\(\sqrt{3}\))²
= x² – 4x + 4 – 3
= x² – 4x + 1
is a factor of p(x).

Then, Quotient = x² – 2x – 35
= x² – 7x + 5x – 35
= x(x – 7) + 5(x – 7)
=(x – 7)(x + 5)
x – 7 = 0 gives x = 7 and x + 5 = 0 gives x = -5.
Hence, the other zeroes of the given polynomial are 7 and -5.

Question 5.
If the polynomial x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:

But, the remainder is given to be x + a.
Hence, comparing the coefficients of x and the constant term, we get
2k – 9 = 1 and k² – 8k + 10 = a
Now, 2k – 9 = 1
∴ 2k = 10
∴ k = 5
and a = k² – 8k + 10
∴ a = (5)² – 8(5) + 10
∴ a = 25 – 40 + 10
∴ a = -5
Thus, k = 5 and a = -5.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 Polynomials Exercise 2.3

Question 1.
Divide the polynomial p (x) by the polynomial g(x) and find the quotient and remainder in each of the following:
1. p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
2. p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
3. p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
Solution:
1.

Quotient x – 3, Remainder = 7x – 9

2. p(x) = x⁴ – 3x² + 4x + 5
= x⁴ + 0x³ – 3x² + 4x + 5
and g(x) = x² + 1 – x = x² – x + 1

Quotient = x² + x – 3, Remainder = 8

3. p(x) = x⁴ – 5x + 6
= x⁴ + 0x³ + 0x² – 5x + 6
and g(x) = 2 – x² = -x² + 2

Quotient = -x² – 2, Remainder = – 5x + 10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
1. t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
2. x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
3. x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:
1.

As the remainder is 0, t² – 3 is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

2.

As the remainder is 0, x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

3.

As the remainder is not 0, x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x + 1.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)
Solution:
Since \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\) are given two zeroes of the polynomial, \(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=x^2-\frac{5}{3}\) is a factor of the given polynomial. Then, to obtain the other zeroes of the polynomial, we divide it by x² – \(\frac{5}{3}\)

Now,
3x² + 6x + 3 = 3(x² + 2x + 1)
= 3(x + 1)²
= 3(x + 1)(x + 1)
Hence, the two zeroes of 3x² + 6x + 3 are 1 and – 1.
Hence, the two zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5 other than the given zeroes are 1 and -1.

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
Here, dividend p(x) = x³ – 3x² + x + 2, quotient q(x) = (x – 2) and remainder r(x) = (-2x + 4).
Now, p(x) = g(x) × q(x) + r(x)
∴ x³ – 3x² + x + 2 = g(x) × (x – 2) + (-2x + 4)
∴ (x³ – 3x² + x + 2) – (-2x + 4) = g(x) × (x – 2)
∴ x³ – 3x² + 3x – 2 = g(x) × (x – 2)
∴ g(x) = \(\frac{x^3-3 x^2+3 x-2}{x-2}\)

Hence, g(x) = x² – x + 1.

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
1. deg p(x) = deg q(x)
2. deg q(x) = deg r(x)
3. deg r(x) = 0.
Solution:
1. deg p (x) = deg q (x) implies that deg g (x) = 0. i.e., g(x) is a non-zero constant. One such example can be given as p (x) = 3x² + 15x + 13, g(x) = 3, q(x) = x² + 5x + 4 and r(x) = 1, which satisfies the division algorithm as:
3x² + 15x + 13 = 3(x² + 5x + 4) + 1.

2. deg q(x) = deg r (x) implies that deg g (x) > deg q(x), because
deg g (x) > degr (x). One such example can be given as p (x) = x³ + 5x² + 2x + 7, g(x) = x² + 1, q(x) = x + 5 and r(x) = x + 2, which satisfies the division algorithm as:
x³ + 5x² + 2x + 7 = (x² + 1)(x + 5) + (x + 2).

3. deg r(x) = 0 implies that the remainder is a constant. One such example can be given as p (x) = x³ + 4x² + 5x + 9, g(x) = x + 3, q(x) = x² + x + 2 and r(x) = 3, which satisfies the division algorithm as:
x³ + 4x² + 5x + 9 = (x + 3)(x² + x + 2) + 3.
Note: There can be several examples in each of the above cases.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 Polynomials Exercise 2.2

Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients :
1. x² – 2x – 8
2. 4s² – 4s + 1
3. 6x² – 3 – 7x
4. 4u² + 8u
5. t² – 15
6. 3x² – x – 4
Solution:
1. x² – 2x – 8 = x² – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x – 4)(x + 2)
So, the value of x² – 2x – 8 is zero, when
x – 4 = 0 or x + 2 = 0, i.e., when x = 4 or x = -2.
Hence, the zeroes of polynomial x² – 2x – 8 are 4 and -2.
Now,
Sum of zeroes = 4 + (-2)
= 2
= \(\frac{-(-2)}{1}\)
= \(\frac{-(\text { Coefficient of } x)}{\text { Coefficient of } x^2}\)
and Product of zeroes = (4) (-2)
= -8
= \(\frac{-8}{1}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

2. 4s² – 4s + 1 = 4s² – 2s – 2s + 1
= 2s (2s – 1) -1 (2s – 1)
= (2s – 1)(2s – 1)
So, the value of 4s² – 4s + 1 is zero, when \(\frac{1}{2}\) or
s = \(\frac{1}{2}\)
2s – 1 = 0 or 2s – 1 = 0, i.e., when s = 2
Hence, the zeroes of polynomial 4s² – 4s + 1 are \(\frac{1}{2}\) and \(\frac{1}{2}\) (both equal).
Now,

3. 6x² – 3 – 7x = 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (2x – 3)(3x + 1)
So, 6x² – 3 – 7x = 0 when 2x – 3 = 0 or 3x + 1 = 0,
i.e., when x = \(\frac{3}{2}\) or x = –\(\frac{1}{3}\).
Hence, the zeroes of polynomial 6x² – 3 – 7x are \(\frac{3}{2}\) and –\(\frac{1}{3}\).
Now,

4. 4u² + 8u = 4u (u + 2)
So, 4u² + 8u = 0 when 4u = 0 or u + 2 = 0,
i.e., when u = 0 or u = -2.
Hence, the zeroes of polynomial 4u² + 8u are 0 and -2.
Now,
Sum of zeroes = 0 + (-2)
= -2
= \(\frac{-(8)}{4}\)
= \(\frac{-(\text { Coefficient of } u)}{\text { Coefficient of } u^2}\)
and
Product of zeroes = (0)(-2) = 0
= \(\frac{0}{4}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } u^2}\)
Note: In polynomial
4u² + 8u = 4u² + 8u + 0, the constant term is 0.

5. t² – 15 = (t)² – (\(\sqrt{15}\))²
= (t + \(\sqrt{15}\)) (t – \(\sqrt{15}\))
So, t² – 15 = 0 when t + \(\sqrt{15}\) = 0 or
t – 15 = 0, i.e., when t = –\(\sqrt{15}\) or t = \(\sqrt{15}\).
Hence, the zeroes of polynomial t² – 15 are –\(\sqrt{15}\) and \(\sqrt{15}\).
Now,
Sum of zeroes = (\(-\sqrt{15}\)) + (\(\sqrt{15}\))
= 0
= \(\frac{-0}{1}\)
= \(\frac{-(\text { Coefficient of } t)}{\text { Coefficient of } t^2}\)
and
Product of zeroes = (\(\sqrt{15}\)) (\(\sqrt{15}\))
= -15
= \(\frac{-15}{1}\)
= \(\frac{\text { Constant term }}{\text { Coefficient of } t^2}\)
Note: In polynomial t² – 15 = t² + 0t – 15, the coefficient of t is 0.

6. 3x² – x – 4 = 3x² + 3x – 4x – 4
= 3x(x + 1) – 4(x + 1)
= (x + 1)(3x – 4)
So, 3x² – x – 4 = 0 when x + 1 = 0 or 3x – 4 = 0, i.e., when x = -1 or x = \(\frac{4}{3}\)
Hence. -1 and \(\frac{4}{3}\) are the zeroes of polynomial 3x² – x – 4.
Now,

Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:
1. \(\frac{1}{4}\), -1
2. \(\sqrt{2}\), \(\frac{1}{3}\)
3. 0, \(\sqrt{5}\)
4. 1, 1
5. \(-\frac{1}{4}, \frac{1}{4}\)
6. 4, 1
Solution:
1. \(\frac{1}{4}\), -1
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given,
α + β = \(\frac{1}{4}\) = \(\frac{-b}{a}\)
and αβ = -1 = \(\frac{c}{a}\)
If a = 4, then b = -1 and c = -4.
So, one quadratic polynomial satisfying the given condition is 4x² – x – 4.
In general, a quadratic polynomial satisfying the given condition is k(4x² – x – 4), where k is a non-zero real number.

2. \(\sqrt{2}\), \(\frac{1}{3}\)
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given,
α + β = \(\sqrt{2}\) = \(\frac{-b}{a}\)
and αβ = \(\frac{1}{3}\) = \(\frac{c}{a}\)
If a = 3, then b = -3\(\sqrt{2}\) and c = 1
So, one quadratic polynomial satisfying the given condition is 3x² – 3\(\sqrt{2}\)x + 1.
In general, a quadratic polynomial satisfying the given condition is k(3x² – 3\(\sqrt{2}\)x + 1).
where k is a non-zero real number.

3. 0, \(\sqrt{5}\)
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given, α + β = 0 = \(\frac{-b}{a}\)
and αβ = \(\sqrt{5}\) = \(\frac{c}{a}\)
If a = 1, then b = 0 and c = \(\sqrt{5}\).
So, one quadratic polynomial satisfying the given condition is x² + \(\sqrt{5}\).
In general, a quadratic polynomial satisfying the given condition is k(x² + \(\sqrt{5}\)), where k is a non-zero real number.

4. 1, 1
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given.
α + β = 1 = \(\frac{-b}{a}\)
and αβ = 1 = \(\frac{c}{a}\)
If a = 1, then b = -1 and c = 1.
So, one quadratic polynomial satisfying the given condition is x² – x + 1.
In general, a quadratic polynomial satisfying the given condition is k(x² – x + 1), where k is a non-zero real number.

5. \(-\frac{1}{4}, \frac{1}{4}\)
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given,
α + β = \(-\frac{1}{4}\) = \(\frac{-b}{a}\)
and αβ = \(\frac{1}{4}\) = \(\frac{c}{a}\)
If a = 4, then b = 1 and c = 1.
So, one quadratic polynomial satisfying the given condition is 4x² + x + 1.
In general, a quadratic polynomial satisfying the given condition is k(4x² + x + 1), where k is a non-zero real number.

6. 4, 1
Let the quadratic polynomial be ax² + bx + c and its zeroes be α and β.
Then, as per given.
α + β = 4 = \(\frac{-b}{a}\)
and αβ = 1 = \(\frac{c}{a}\)
If a = 1, then b = -4 and c = 1.
So, one quadratic polynomial satisfying the given condition is x² – 4x + 1.
In general, a quadratic polynomial satisfying the given condition is k(x² – 4x + 1), where k is a non-zero real number.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.3

Question 1.
Find the area of the triangle whose vertices are :
1. (2, 3), (-1, 0), (2, -4)
2. (5, 1), (3, 5), (5, 2)
Answer:
1. Let A (2, 3), B(-1, 0) and C(2, – 4) be the vertices of ΔABC. Then, using the formula, the area of ΔABC is given by \(\frac{1}{2}\)[2 (0 + 4) + (-1) (- 4 – 3) + 2(3 – 0)]
= \(\frac{1}{2}\)(8 + 7 + 6)
= \(\frac{21}{2}\) sq units
Thus, the area of the triangle with given vertices is \(\frac{21}{2}\) sq units.

2. The vertices of the triangle are given to be (-5, -1), (3, – 5) and (5, 2).
Then, using the formula, the area of the triangle is given by
= \(\frac{1}{2}\)[-5(-5 – 2) + 3(2 + 1) + 5 (-1 + 5)]
= \(\frac{1}{2}\)(35 + 9 + 20)
= \(\frac{1}{2}\)(64)
= 32 sq units
Thus, the area of the triangle with given vertices is 32 sq units.

Question 2.
In each of the following find the value of ‘k’, for which the points are collinear:
1. (7, -2), (5, 1), (3, k)
2. (8, 1), (k, – 4), (2, – 5)
Answer:
1. If the points (7, -2), (5, 1) and (3, k) are collinear, then the area of imaginary triangle formed by those points as vertices must be zero.
∴ \(\frac{1}{2}\)[7 (1 – k) + 5 (k + 2) + 3(- 2 – 1)] = 0
∴ \(\frac{1}{2}\)[7 – 7k + 5k + 10 – 9] = 0
∴ – 2k + 8 = 0
∴ 2k = 8
∴ k = 4

2. If the points (8, 1), (k, – 4) and (2, – 5) are collinear, then the area of imaginary triangle formed by those points as vertices must be zero.
∴ \(\frac{1}{2}\)[8 (- 4 + 5) + k(-5 – 1) + 2(1 + 4)] = 0
∴ 8 – 6k + 10 = 0
∴ 18 = 6k
∴ k = 3

Question 3.
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are (0, – 1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Answer:
Let A (0, – 1), B (2, 1) and C(0, 3) be the vertices of ΔABC and let D, E and F be the midpoints of the sides BC, CA and AB respectively.
Then, coordinates of D = (\(\frac{2+0}{2}, \frac{1+3}{2}\)) = (1, 2)
Coordinates of E = (\(\frac{0+0}{2}, \frac{3-1}{2}\)) = (0, 1)
Coordinates of F = (\(\frac{0+2}{2}, \frac{-1+1}{2}\)) = (1, 0)
Area of ΔDEF
= \(\frac{1}{2}\)[1(1 – 0) + 0(0 – 2) + 1 (2 – 1)]
= \(\frac{1}{2}\)(1 + 0 + 1)
= 1 sq unit
Area of ΔABC
= \(\frac{1}{2}\)[0(1 – 3) + 2(3 + 1) + 0 (- 1 – 1)]
= \(\frac{1}{2}\)(0 + 8 + 0)
= 4 sq units
Then, area of ΔDEF : area of ΔABC = 1 : 4.
Thus, the area of triangle formed by joining the midpoints of the sides of the triangle with given vertices is 1 sq unit and the required ratio of areas is 1 : 4.

Question 4.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, – 2), (- 3, – 5), (3, – 2) and (2, 3).

Answer:
Let A(- 4, – 2), B(- 3, – 5), C(3, – 2) and D (2, 3) be the vertices of quadrilateral ABCD.
Drawing diagonal AC, we get two triangles ABC and ADC.
The vertices of ΔABC are A (-4, – 2), B(-3, 5) and C(3, -2).
Area of ΔABC
= \(\frac{1}{2}\)[-4(-5 + 2) + (-3) (-2 + 2) + 3(-2 + 5)]
= \(\frac{1}{2}\)[12 + 0 + 9]
= \(\frac{21}{2}\) sq units
The vertices of ΔADC are A(-4, -2), D(2, 3) and C(3, -2).
∴ Area of ΔADC
= \(\frac{1}{2}\)[- 4(3 + 2) + 2(- 2 + 2) + 3(- 2 – 3)]
= \(\frac{1}{2}\)(-20 + 0 – 15)
= \(\frac{1}{2}\)(- 35)
But area of a triangle cannot be negative.
Hence, we take the numerical value.
∴ Area of ΔADC = \(\frac{35}{2}\)sq units.
Now, area of quadrilateral ABCD
= area of ΔABC + area of ΔADC
= (\(\frac{21}{2}=\frac{35}{2}\)) sq units
= 28 sq units
Thus, the area of the given quadrilateral is 28 sq units.

Question 5.
You have studied in Class IX, that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A(4, 6), B (3, – 2) and C (5, 2).
Answer:

A (4, – 6) , B (3, – 2) and C (5, 2) are the vertices of ΔABC.
Let AD be a median of ΔABC.
Then, D is the midpoint of BC.
∴ Coordinates of D are (\(\frac{3+5}{2}, \frac{-2+2}{2}\)), ie., (4, 0)
Area of ΔABC
= \(\frac{1}{2}\)[4(- 2 – 2) + 3(2 + 6) + 5(- 6 + 2)]
= \(\frac{1}{2}\)[-16 + 24 – 20]
= \(\frac{1}{2}\) (-12)
= 6 sq units (∵ Area cannot be negative.) ………(1)
Vertices of ΔADB are A (4, – 6), D (4, 0) and B (3, -2)
Area of ΔADB
= \(\frac{1}{2}\)[4(0 + 2) + 4(- 2 + 6) + 3(- 6 – 0)]
= \(\frac{1}{2}\)[18 + 16 – 18]
= 3 sq units ……(2)

Vertices of ΔADC are A (4, – 6), D (4, 0) and C (5, 2).
Area of ΔADC
= \(\frac{1}{2}\)[4 (0 – 2) + 4 (2 + 6) + 5 (- 6 – 0)]
= \(\frac{1}{2}\)[- 8 +32 – 30]
= \(\frac{1}{2}\)[-6]
= 3 sq units (∵ Area cannot be negative.) ……(3)
From (1), (2) and (3), we get
Area of ΔADB = Area of ΔADC = \(\frac{1}{2}\) Area of ΔABC
Thus, median AD divides ΔABC into two triangles ADB and ADC of equal areas.
The same result can be proved for other two medians BE and CF.
Hence, the statement that “A median of a triangle divides it into two triangles of equal areas.” is verified.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 Polynomials Exercise 2.1

Question 1.

Solution:
1. The number of zeroes is 0 as the graph being parallel to the x-axis does not intersect it.
2. The number of zeroes is 1 as the graph intersects the x-axis at one point only.
3. The number of zeroes is 3 as the graph intersects the x-axis at three points.
4. The number of zeroes is 2 as the graph intersects the x-axis at two points.
5. The number of zeroes is 4 as the graph intersects the x-axis at four points.
6. The number of zeroes is 3 as the graph intersects the x-axis at three points.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 1 Real Numbers Ex 1.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 1 Real Numbers Exercise 1.4

Question 1.
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
1. \(\frac{13}{3125}\)
2. \(\frac{17}{8}\)
3. \(\frac{64}{455}\)
4. \(\frac{15}{1600}\)
5. \(\frac{29}{343}\)
6. \(\frac{23}{2^3 5^2}\)
7. \(\frac{129}{2^2 5^7 7^5}\)
8. \(\frac{6}{15}\)
9. \(\frac{35}{50}\)
10. \(\frac{77}{210}\)
Solution:
1. \(\frac{13}{3125}\)
Here, the denominator q(5⁵) is of the form 2ⁿ5^m with n = 0 and m = 5.
Hence, the decimal expansion of \(\frac{13}{3125}\) is terminating.

2. \(\frac{17}{8}\) = \(\frac{17}{2^3}\)
Here, the denominator q(2³) is of the form 2ⁿ5^m with n = 3 and m = 0.
Hence, the decimal expansion of \(\frac{17}{8}\) terminating.

3. \(\frac{64}{455}=\frac{64}{5 \times 7 \times 13}\)
Here, the denominator q(5 × 7 × 13) is not of the form 2ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{64}{455}\) is non-terminating repeating.

4. \(\frac{15}{1600}=\frac{3}{320}=\frac{3}{2^6 \times 5^1}\)
Here, the denominator q(2⁶ × 5¹) is of the form 2ⁿ5^m with n = 6 and m = 1.
Hence, the decimal expansion of \(\frac{15}{1600}\) is terminating.

5. \(\frac{29}{343}=\frac{29}{7^3}\)
Here, the denominator q(7³) is not of the form 2ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{29}{343}\) is non-terminating repeating.

6. \(\frac{23}{2^3 5^2}\)
Here, the denominator q(2³5²) is of the form 2ⁿ5^m with n = 3 and m = 2.
Hence, the decimal expansion of \(\frac{23}{2^3 5^2}\) is terminating.

7. \(\frac{129}{2^2 5^7 7^5}\)
Here, the denominator q (2² × 5⁷ × 7⁵) is not of the form 2ⁿ5^m, where n and m are non-negative integers. Hence, the decimal expansion of \(\frac{129}{2^2 5^7 7^5}\) is non-terminating repeating.

8. \(\frac{6}{15}=\frac{2 \times 3}{3 \times 5}=\frac{2}{5^1}\)
Here, the denominator q(5¹) is of the form 2ⁿ5^m with n = 0 and m = 1.
Hence, the decimal expansion of \(\frac{6}{15}\) is terminating.

9. \(\frac{35}{50}=\frac{5 \times 7}{2 \times 5 \times 5}=\frac{7}{2^1 \times 5^1}\)
Here, the denominator q(2¹ × 5¹) is of the form 2ⁿ5^m with n = 1 and m = 1.
Hence, the decimal expansion of \(\frac{35}{50}\) is terminating.

10. \(\frac{77}{210}=\frac{7 \times 11}{2 \times 3 \times 5 \times 7}=\frac{11}{2 \times 3 \times 5}\)
Here, the denominator q(2 × 3 × 5) is not of the form 2²ⁿ5^m, where n and m are non-negative integers.
Hence, the decimal expansion of \(\frac{77}{210}\) is non-terminating repeating.

Question 2.
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solution:

Question 3.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form \(\frac{p}{q}\), what can you say about the prime factors of q?
1. 43.123456789
2. 0.120120012000120000…
3. \(43 . \overline{123456789}\)
Solution:
1. The given number 43.123456789 is a rational number as its decimal expansion is terminating
Since the decimal expansion of the given number is terminating, in the \(\frac{p}{q}\) form of the number, the prime factors of q will only be 2 or 5 or both. (Theorem 1.5)

2. The given number 0.120120012000120000…. is an irrational number as its decimal expansion is non-terminating non-repeating.

3. The given number \(43 . \overline{123456789}\) is a rational number as its decimal expansion is an non-terminating repeating.
Since the decimal expansion of the given number is non-terminating repeating, in the \(\frac{p}{q}\) form of the number, the prime factors of q will contain at least one prime other than 2 and 5. (Converse of Theorem 1.7)

Jharkhand Board JAC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.2

Question 1.
Find the coordinates of the point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2 : 3.
Answer:
Let P(x, y) be the required point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2 : 3.
Then, using the section formula, we get
x = \(\frac{2(4)+3(-1)}{2+3}\) = \(\frac{8-3}{5}\) = 1 and
y = \(\frac{2(-3)+3(7)}{2+3}\) = \(\frac{-6+21}{5}\) = 3
Thus, the coordinates of the point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2 : 3 are (1, 3).

Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, – 1) and (- 2, – 3).
Answer:
Let A (4, – 1) and B (- 2, – 3) be the given points and let P and Q be the points of trisection of AB.

Then, AP = PQ = QB
Hence, P divides AB in the ratio 1 : 2.
Therefore, the coordinates of P, by applying the section formula, are
(\(\frac{1(-2)+2(4)}{1+2}, \frac{1(-3)+2(-1)}{1+2}\)) = (2, – \(\frac{5}{3}\))
Now, Q divides AB in the ratio 2 : 1.
Therefore, the coordinates of Q, by applying the section formula, are
(\(\frac{2(-2)+1(4)}{2+1}, \frac{2(-3)+1(-1)}{2+1}\)) = (0, – \(\frac{7}{3}\))
Thus, the coordinates of the points of trisection of the line segment joining (4, – 1) and (- 2, – 3) are (2, – \(\frac{5}{3}\)) and (0, – \(\frac{7}{3}\)).

Alternative method for Q :
Here, Q is the midpoint of the line segment joining P(2, – \(\frac{5}{3}\)) and B(- 2, – 3). Therefore, by applying the midpoint formula, the coordinates of Q are
(\(\frac{2+(-2)}{2}\), \(\frac{-\frac{5}{3}+(-3)}{2}\)) = (0, – \(\frac{7}{3}\))

Question 3.
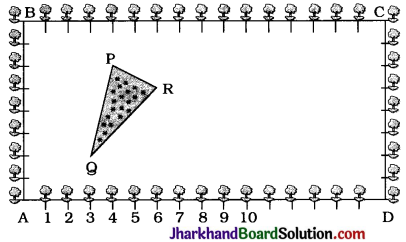
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in the given figure. Niharika runs \(\frac{1}{4}\)th the distance AD on the 2nd line and posts a green flag. Preet runs \(\frac{1}{5}\)th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

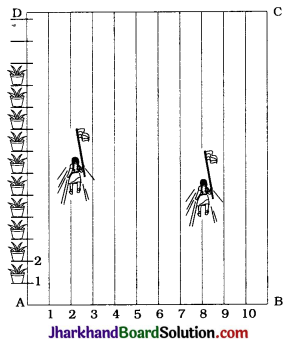
Let us consider rectangle ABCD as coordinate plane with A as the origin.
Then, AD = 100 m and each lane number will indicate its distance on the x-axis. Niharika \(\frac{1}{4}\)th the distance AD.
∴ Distance covered by Niharika = \(\frac{1}{4}\) × 100 m
= 25 m
Niharika runs on the second line.

Hence, the coordinates of the point N where Niharika posts the green flag are (2, 25). Following the same notations, the coordinates of the point P where Preet posts the red flag are (8, 20).
To find the distance (in metres) between the two flags, we have to find the length of join of N (2, 25) and P(8, 20).

Now, Rashmi has to post a blue flag exactly halfway between the green flag and the red flag.
So, we have to find the midpoint R of the join of N (2, 25) and P(8, 20).

Then, the coordinates of R, using the midpoint formula, are
(\(\frac{2+8}{2}, \frac{25+20}{2}\)) = (5, 22.5)
This suggest that Rashmi should post the blue flag on the fifth line at distance of 22.5 m from AB.
Thus, the distance between the green flag and the red flag is \(\sqrt{61}\)m and Rashmi should post the blue flag on the 5th line at distance 22.5 m from AB.

Question 4.
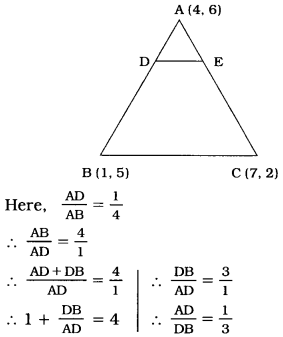
Find the ratio in which the line segment joining the points (- 3, 10) and (6, – 8) is divided by (- 1, 6).
Answer:
Let P(- 1, 6) divide internally the line segment joining the points A(- 3, 10) and B (6, – 8) in the ratio m₁ : m₁.
Using the section formula, we get

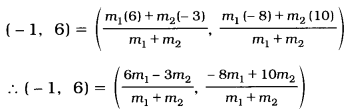
Comparing the x-coordinates on both the sides, we get
∴ – 1 = \(\frac{6 m_1-3 m_2}{m_1+m_2}\)
∴ – m₁ – m< sub>2 = 6m₁ – 3m₂
∴ 7m₁ = 2m₂
∴ \(\frac{m_1}{m_2}=\frac{2}{7}\)
∴ m₁ : m₂ = 2 : 7
Then, to verify the y-coordinate,

Thus, the point (- 1, 6) divides the line segment joining the points (- 3, 10) and (6, – 8) in the ratio 2 : 7.

Question 5.
Find the ratio in which the line segment joining A(1, 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.
Answer:
Let the ratio in which the line segment joining A(1, – 5) and B(- 4, 5) is divided by the x-axis be k : 1.
Then, by the section formula, the coordinates of the point which divides AB in the ratio k : 1 are
(\(\frac{k(-4)+1(1)}{k+1}, \frac{k(5)+1(-5)}{k+1}\)), i.e. (\(\frac{1-4 k}{k+1}\), \(\frac{5 k-5}{k+1}\))
Now, the point of division is on the x-axis.
Hence, its y-coordinate is 0.
∴ \(\frac{5 k-5}{k+1}\) = 0
∴ k = 1
Hence, the required ratio k : 1 is 1 : 1.
Now, the coordinates of the point of division

Thus, the x-axis divides the line segment joining A(1, – 5) and B(- 4, 5) in the ratio 1 : 1 at the point (-\(\frac{3}{2}\), 0).

Question 6.
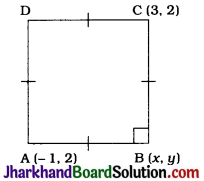
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer:
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5) be the vertices of parallelogram ABCD. As ABCD is a parallelogram, its diagonals AC and BD bisect each other.
∴ Midpoint of AC = Midpoint of BD

Question 7.
Find the coordinates of a point A, where. AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
Answer:
Let the coordinates of A be (x, y).
In a circle, centre is the midpoint of every diameter.
Here, AB is a diameter and (2, – 3) is the centre.
∴ Midpoint of AB = (2, – 3)
∴ (\(\frac{x+1}{2}, \frac{y+4}{2}\)) = (2, – 3)
∴ \(\frac{x+1}{2}\) = 2 and \(\frac{y+4}{2}\) = – 3
∴ x = 3 and y = – 10
Thus, the coordinates of A are (3, -10).

Question 8.
If A and B are (- 2, – 2) and (2, 4). respectively, find the coordinates of P such that AP = \(\frac{3}{7}\)AB and P lies on the line segment AB.
Answer:
A(- 2, – 2) and B (2, – 4) are given points and point P(x, y) lies on line segment AB such that AP = \(\frac{3}{7}\)AB.
Then, PB = AB – AP = AB – \(\frac{3}{7}\)AB = \(\frac{4}{7}\)AB.
Now, \(\frac{AP}{PB}\) = \(\frac{\frac{3}{7} \mathrm{AB}}{\frac{4}{7} \mathrm{AB}}\) = \(\frac{3}{4}\)
Thus, P(x, y) divides AB in the ratio 3 : 4.
Then, by section formula
(x, y) = (\(\frac{3(2)+4(-2)}{3+4}, \frac{3(-4)+4(-2)}{3+4}\))
∴ (x, y) = (-\(\frac{2}{7}\), – \(\frac{20}{7}\))
Thus, the coordinates of P are (-\(\frac{2}{7}\), – \(\frac{20}{7}\))

Question 9.
Find the coordinates of the points which divide the line segment joining A(-2, 2) and B (2, 8) into four equal parts.

Answer:
Let P, Q and R be the points which divide the line segment AB joining A(-2, 2) and B(2, 8) into four equal parts.
Then, Q is the midpoint of AB.
Hence, by midpoint formula, the coordinates of Q are
(\(\frac{-2+2}{2}, \frac{2+8}{2}\)) = (0, 5)
Now, P is the midpoint of Ag.
Hence, by midpoint formula, the coordinates of P are
(\(\frac{-2+0}{2}, \frac{2+5}{2}\)) = (-1, \(\frac{7}{2}\))
Again, R is the midpoint of QB.
Hence, by midpoint formula, the coordinates of R are
(\(\frac{0+2}{2}, \frac{5+8}{2}\)) = (1, \(\frac{13}{2}\))
Thus, the coordinates of the required points are (- 1, \(\frac{7}{2}\)), (0, 5) and (1, \(\frac{13}{2}\)).

Question 10.
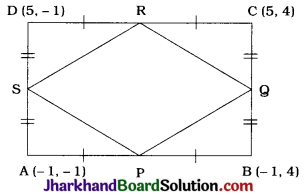
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (- 1, 4) and (- 2, – 1) taken in order.
[Hint: Area of a rhombus = \(\frac{1}{2}\) (product of its diagonals)]
Answer:
Let A (3, 0), B(4, 5), C(-1, 4) and D(-2, -1) be the vertices of rhombus ABCD.
Diagonal AC = \(\sqrt{(3+1)^2+(0-4)^2}\)
= \(\sqrt{32}\) = 4 \(\sqrt{2}\) units
Diagonal BD = \(\sqrt{(4+2)^2+(5+1)^2}\)
= \(\sqrt{72}\) = 6\(\sqrt{2}\) units
Now, area of a rhombus
= \(\frac{1}{2}\)(Products of its diagonals)
∴ Area of rhombus ABCD = \(\frac{1}{2}\) × AC × BD
= \(\frac{1}{2}\) × 4\(\sqrt{2}\) × 6\(\sqrt{2}\)
= 24 sq units
Thus, the area of given rhombus with vertices (3, 0), (4, 5), (- 1, 4) and (- 2, – 1) is 24 sq units.