Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1
Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting ?) Represent this situation algebraically and graphically.
Solution:
Let the present age of Aftab be x years and the present age of his daughter be y years. Then, seven years ago, the age of Aftab was x – 7 years and the age of his daughter was y – 7 years.
So, from the given data.
x – 7 = 7(y – 7)
∴ x – 7 = 7y – 49
x – 7y + 42 = 0 …….. (1)
Similarly, three years from now, the age of Aftab will be x + 3 years and the age of his daughter will be y + 3 year.
So, according to the given data,
x + 3 = 3(y + 3)
∴ x + 3 = 3y + 9
∴ x – 3y – 6 = 0 ….. (2)
Thus, the equations x – 7y + 42 = 0 and x – 3y – 6 = 0 represent the given situation algebraically.
To represent the given situation graphically. we draw the graphs of both the equations.
x – 7y + 42 = 0
∴ y = \(\frac{42+x}{7}\)
| x | 0 | 35 |
| y | 6 | 11 |
x – 3y – 6 = 0
∴ y = \(\frac{x-6}{3}\)
| x | 0 | 30 |
| y | -2 | 8 |
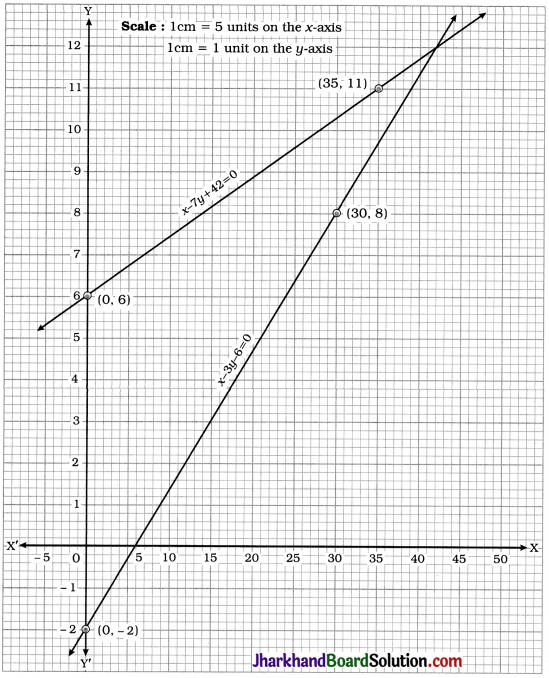
The above graph represents the situation graphically.
We observe that the lines intersect at point (42, 12).
Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let the cost of one bat be ₹ x and the cost of one ball be ₹ y.
Then, the total cost of 3 bats is ₹ 3x and that of 6 balls is ₹ 6y. From the data, the total cost is ₹ 3900.
∴ 3x + 6y = 3900
∴ x + 2y = 1300
Similarly, the cost of 1 bat is ₹ x and the total cost of 3 balls is ₹ 3y. From the data, the total cost is ₹ 1300.
∴ x + 3y = 1300
Thus, the equations x + 2y = 1300 and x + 3y = 1300 represent the given situation algebraically.
To represent the given situation geometrically. we draw the graphs of both the equations.
x + 2y = 1300
| x | 100 | 1300 |
| y | 600 | 0 |
x + 3y = 1300
| x | 100 | 1300 |
| y | 400 | 0 |
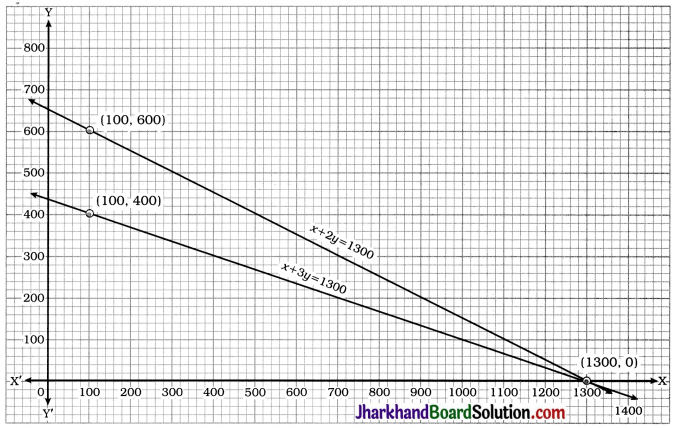
The above graph represents the situation geometrically.
We observe that the lines intersect at point (1300, 0).
Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be After a month, the cost of 4 kg of apples and 2 kg of grapes is 300. Represent the situation algebraically and geometrically.
Solution:
Let the cost of 1 kg of apples be ₹ x and the cost of 1 kg of grapes be ₹ y.
Then, from the given data, 2x + y = 160 and 4x + 2y = 300.
Thus, the equations 2x + y = 160 and 4x + 2y = 300 represent the given situation algebraically.
To represent the given situation geometrically. we draw the graphs of both the equations.
2x + y = 160
| x | 0 | 80 |
| y | 160 | 0 |
4x + 2y = 300
| x | 0 | 75 |
| y | 150 | 0 |
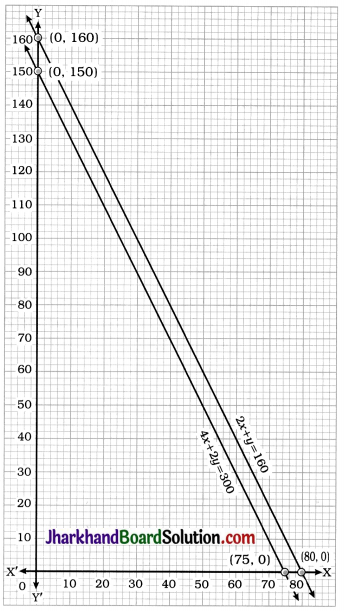
The above graph represents the situation geometrically.
We observe that the lines are parallel.