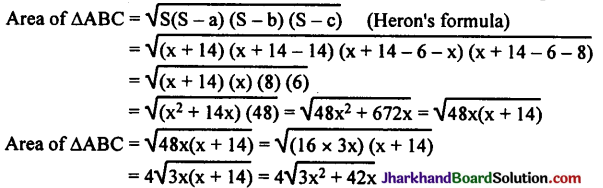Month: April 2023

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.4

Use π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:

Question 2.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
C.S.A. of the frustum = πl(r₁ + r₂)
2πr₁ = 18
r₁ = \(\frac{18}{2 \pi}=\frac{9}{\pi}\)
2πr₂ = 6
r₂ = \(\frac{6}{2 \pi}=\frac{3}{\pi}\)
C.S.A. of the frustum = xl(r₁ + r₂)
= π × \(4\left[\frac{9}{\pi}+\frac{3}{\pi}\right]\)
= π × 4 × \(\frac{12}{\pi}\)
= 48 cm².3

Question 3.
A fez, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
r₁ = 4, r₂ = 10, l = 15
Area of the material used = C.S.A. of the frustum + Area of the circular top
= πl(r₁ + r₂) + πr₁²
= \(\frac{22}{7}\) × 15 (4 + 10) + π × 4²
= \(\frac{22}{7}\) × 15 × 14 + \(\frac{22}{7}\) × 16
= \(\frac{22}{7}\)(210 + 16)
= \(\frac{22}{7}\) × 226
= \(\frac{4972}{7}\)
= 710\(\frac{2}{7}\) cm².

Question 4.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs. 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs. 8 per 100 cm². (Take π = 3.14).
Solution:
Volume of the milk = Volume of the container = Volume of the frustum
= \(\frac{1}{3}\)πh(r₁² + r₂² + r₁r₂)   [r₁ = 20, r₂ = 8, h = 16]
= \(\frac{1}{3}\) × 3.14 × 16[(20)² + (8)² + (20 × 8)]
= \(\frac{1}{3}\) × 3.14 × 16[400 + 64 + 160]
= \(\frac{1}{3}\) × 3.14 × 16 × 624 c.c. [1 litre 1000 cc]
= \(\frac{1}{3}\) × \(\frac{3.14 \times 16 \times 624}{1000}\) litres.
Cost of the milk = \(\frac{3.14 \times 16 \times 624}{3 \times 1000}\)
= \(\frac{3.14 \times 1664}{25}\)
= 3.14 × 66.56
= 208.99 = Rs. 209.
Area of the metal sheet used = πl(r₁ + r₂) + πr₂² [r₁ = 20, r₂ = 8, h = 16]

Area of the metal sheet used = πl(r₁ + r₂) + πr₂²
= 3.14 × 20(20 + 8) + 3.14 × 8²
= 3.14 × 20 × 28 + 3.14 × 64
= 3.14[(20 × 28) + 64]
= 3.14(560 + 64)
= 3.14 × 624 sq. cms.
Cost of the metal sheet = Area × Rate
= 3.14 × 624 × rate
= \(\frac{3.14 \times 624 \times 8}{100}\)
= 3.14 × 624 × 0.08
= 3.14 × 49.92
= 156.7488
= Rs. 156.75.

Question 5.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \(\frac{1}{6}\) cm, find the length of the wire.
Solution:

Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.1

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Solution :
Circumference of circle 1 = 2πr
= 2 × π × 19 cm = 2π × 19
Circumference of circle 2 = 2 × π × 9 cm = 2π × 9
Sum of the circumferences = (2π × 19) + (2π × 9)
= 2π(19 + 9)
= 2π 28
= 56 π.
Circumference of circle 3 = 56π.
2πr = 56π
r = \(\frac{56π}{2π}\)
= 28 cm.

Alternative Method:
r₁ = 19 cm, r₂ = 9 cm, R = ?
2πr₁ + 2πr₂ = 2πR (given)
2π(г₁ + r₂) = 2πR
(19 + 9) = R
∴ R = 28 cm.

Question 2.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Solution :
Area of circle 1 = π × 8² cm²
Area of circle 2 = π × r² = π × 6²
Sum of the areas = π(8² + 6²)
= π(64 + 36)
= 100π
Area of circle 3 = 100 π
πr² = 100 π
r² = \(\frac{100π}{π}\) = 100
∴ r = 10 cm.

Alternative Method:
πr₁² + πr₂² = πR²
π(r₁² + r₂²) = πR²
8² + 6² = R²
64 + 36 = R²
\(\sqrt{100}\) = R
∴ R = 10 cm.

Question 3.
The figure depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Solution :

KG = GE = EC = CA = AO = OB = 10.5 cm
Area of the gold band = πr²
= \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
r = \(\frac{AB}{2 }=\frac{21}{2}\) = 10.5
= \(\frac{33 \times 21}{2}=\frac{693}{2}\)
= 346.5 cm².

Area of the red band d = 21 + 10.5 + 10.5 = 42 cm.
= (\(\frac{22}{7} \times \frac{42}{2} \times \frac{42}{2}\)) – 346.5(area of the gold circle)
= (66 × 21) – 346.5
= 1386 – 346.5 = 1039.5 cm².

Area of the blue band d = 6 × 10.5 = 63
= (\(\frac{22}{7} \times \frac{63}{2} \times \frac{63}{2}\)) – area of the red circle
= \(\frac{99 \times 63}{2}\) – (66 × 21)
= \(\frac{6237}{2}\) – 1386
= 3118.5 – 1386.0 = 1732.5 cm²

Area of the black band = d = GH = 8 × 10.5 = 84
= (\(\frac{22}{7} \times \frac{84}{2} \times \frac{84}{2}\)) – area of the blue circle
= \(\frac{22}{7} \times \frac{84}{2} \times \frac{84}{2}\) – (\(\frac{22}{7} \times \frac{63}{2} \times \frac{63}{2}\))
= (132 × 42) – \(\frac{99 \times 63}{2}\)
= 5544.0 – 3118.5 = 2425.5 cm²

Area of the white band = d = KL = 10 × 10.5 = 105
= (\(\frac{22}{7} \times \frac{105}{2} \times \frac{105}{2}\)) – (132 × 42) (area of black circle)
= \(\frac{165 \times 105}{2}\) – (132 × 42)
= \(\frac{17325}{2}\) – 5544
= 8662.5 – 5544.0 = 3118.5 cm².

Question 4.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Solution :
Distance travelled in one revolution = Circumference of the wheel
= 2πr d = 80
= 2 × \(\frac{22}{7} \times \frac{80}{2}=\frac{22 \times 80}{7}\) cm
Distance travelled by the car in 10 min — ?
Speed of the car = 66 km/hr.
Speed of the car = \(\frac{66}{60}\) × 10 = 11 km/min.
= 11 × 1000 mts./min.

Question 5.
Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units.
Solution :
2πr = πr²
2r = r²
Solution :
(A). r = 2 units.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.3

Take π = \(\frac{22}{7}\), unless stated otherwise.

Question 1.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
R = 4.2, r = 6
Volume of the cylinder = Volume of the melted sphere
πr²h = \(\frac{4}{3}\)πR³
3πr²h = 4πR³
h = \(\frac{4 \pi \mathrm{R}^3}{3 \pi \mathrm{r}^2}\)
= \(\frac{4 \times 4.2 \times 4.2 \times 4.2}{3 \times 6 \times 6}\)
= 4 × 1.4 × 0.7 × 0.7
= 5.6 × 0.49
= 2.744 cm.
Height of the cylinder = 2.74 cm.

Question 2.
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
r₁ = 6 cm, r₂ = 8 cm, r₃ = 10 cm.
Let the radius of the resulting sphere be r cm.
Its volume = \(\frac{4}{3}\)πR³
Volume of the resulting sphere = Volume of the sphere of radius r₁ + Volume of the sphere of radius r₂ + Volume of the sphere of radius r₃

Radius of the resulting sphere = 12 cm.

Question 3.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:

Question 4.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4m to form an embankment. Find the height of the embankment.
Solution:
Volume of the earth got by digging the well = πr²h
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 14\)
= 99 cm.
R = 1.5 + 4
r = 1.5

Area of the circular embankment around the well = πR² – πr²
= π[(5.5)² – (1.5)²]
= π(5.5 + 1.5) (5.5 – 1.5)
= π(7) (4).

Question 5.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution:
Volume of ice cream in the cylindrical container =

Alternative Method:
Number of cones will be = \(\frac{\text { Volume of cylinder }}{\text { Volume of cone }}\)
For the cylinder part,
Radius = \(\frac{12}{2}\) = 6 cm, Height = 15 cm
∴ Volume of cylinder = π × r² × h = 540π
For the cone part,
Radius of conical part = \(\frac{6}{2}\) = 3 cm, Height = 12 cm
Radius of hemispherical part = \(\frac{6}{2}\) = 3 cm
Now,
Volume of cone = Volume of conical part + Volume of hemispherical part
\(\left(\frac{1}{3}\right)\) × π × r² × h + \(\left(\frac{2}{3}\right)\) × π × r³
= 36π + 18π
= 54π.
∴ Number of cones = \(\frac{540 \pi}{54 \pi}\) = 10

Question 6.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution:

Question 7.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:

Volume of sand in the bucket = πr²h
= π × 18 × 18 × 32 cc.
Volume of the conical heap of sand = \(\frac{1}{3}\)πr²h
\(\frac{1}{3}\)πr²h = π × 18 × 18 × 32
πr²h = 3 × π × 18 × 18 × 32
πr² × 24 = 3 × π × 18 × 18 × 32
r² = \(\frac{3 \times \pi \times 18 \times 18 \times 32}{\pi \times 24}\)
r² = 18² × 2²
r = 18 × 2 = \(\frac{72}{2}\) = 36 cm.
l² = h² + r²
= (24)² + (36)²
= (24 × 24) + (36 × 36)
= (2 × 12 × 12 × 2) + (3 × 12 × 12 × 3)
= 12² (4 + 9)
= 12² × 13
l = 12\(\sqrt{13}\) cm.

Question 8.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
Quantity of water flowing in the canal in 1 hour = lbh
l = 10 km, b = 6 m, h = 1.5 m
10 × 1000 × 6 × 1.5 cubic metres.
The area this water can irrigate in 1 hour if 8 cm of standing water is needed
= \(\frac{10 \times 1000 \times 6 \times 1.5}{0.08}\)
8 cm = 0.08 mm
Area needed to irrigate in 30 mins. or \(\frac{1}{2}\) hr.

Question 9.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution:
d = 20 cm, r = 10 cm = \(\frac{10}{100}\) = 0.1 mt, h = 3 km = 3 × 1000 m.
Volume of water that comes out of the pipe of diameter 20 cm
= πr²h
= π × 0.1 × 0.1 × 3000
= π × 30 cm.
In 1 hr. (60 mins.), volume of water that flows into the tank = π × 30
In 1 minute = \(\frac{\pi \times 30}{60}=\frac{\pi}{2}\) cm.
Volume of the cylindrical tank = πr²h = π × 5 × 5 × 2. d = 10, r = 5
\(\frac{\pi}{2}\) cubic metres of water will be filled in 1 minute
π × 5 × 5 × 2……. \(\frac{\pi \times 5 \times 5 \times 2 \times 2}{\pi}\) = 100 mins.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.2

Unless stated otherwise, take π = \(\frac{22}{7}\)

Question 1.
A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone equal to its radius. Find the volume of the solid in terms οf π.
Solution:
The given solid is a combination of a cone and a hemisphere.
We have radius of the cone r = Radius of the hemisphere = 1 cm and height of the cone h = 1 cm.

∴ Volume of the solid = Volume of the cone + Volume of the hemisphere

Question 2.
Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Solution:
d = 3 cm, AF = 8 cm = H, Ax = Fy = 2 cm = h, r = \(\frac{3}{2}\)

Volume of the model = Volume of the cone ABC + Volume of the cylinder BCED + Volume of the cone DEF

Question 3.
A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
Solution:

Volume of 1 jamun = Volume of the cylinder + 2 × Volume of the hemisphere

Question 4.
A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.
Solution:

Volume of wood in the stand = Volume of the cuboid – Volume of wood lost in making four conical depressions

Question 5.
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution:
Volume of water in the cone = \(\frac{\pi r^2 h}{3}\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 5 × 5 × 8 cc.
= \(\frac{22 \times 25 \times 8}{21}\) c.c.
When some lead shots are dropped into the vessel, volume of the water that flows out

= \(\frac{1}{4} \times \frac{22 \times 25 \times 8}{21}\)
= \(\frac{22 \times 25 \times 2}{21}\) cc
This is equal to the volume of the lead shots dropped.
Volume of a lead shot = \(\frac{4}{3}\)πr³
Let the no. of lead shots dropped be x.
The volume of x lead shots = Volume of water overflown

Number of lead shots dropped = 100.

Question 6.
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surrounded by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron has approximately 8 g mass. (Use π = 3.14).
Solution:
R = 12, r = 4.
Common factor of 144 and 64 is 16 (HCF)
HCF of 220 and 60 is 20.
1 kg = 1000 gms.

Volume of the given solid = Volume of the bigger cylinder + Volume of the surmounted cylinder
= πR²H + πr²h
= 3.14 × 12² × 220 + 3.14 × 8² × 60
= 3.14 × 144 × 220 + 3.14 × 64 × 60
= 3.14 × 16 × 20(9 × 11 + 4 × 3)
= 3.14 × 320(99 + 12)
= 3.14 × 320 × 111 c.c.
Mass of the solid = Volume × density
= 3.14 × 320 × 111 × 8 gm
= \(\frac{3.14 \times 320 \times 111 \times 8}{1000}\)kg.
= \(\frac{3.14 \times 32 \times 888}{100}\)
= 3.14 × 32 × 8.88
= 892.26 kg.

Question 7.
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:
h = 180 (cylinder), H = 120 (Cone).
Volume of the solid given = Volume of the cone + Volume of the hemisphere

Volume of water left in the cylinder = Volume of water in the cylinder – Volume of the solid immersed

Question 8.
A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Solution:
r = \(\frac{8.5}{2}\), R = \(\frac{2}{2}\) = 1

Volume of water in the vessel = Volume of water in the spherical part + Volume of water in the cylindrical neck.

= 3.14 × 110.354 = 346.51 cm³.
The child’s answer is wrong.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 Constructions Exercise 11.2

In each of the following, give also the justification of the construction:

Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

Steps of construction:
1. Draw a line segment OP = 10 cm.
2. With O as centre and 6 cm as radius draw a circle C₁.
3. Draw the perpendicular bisector of OP. Let x be the midpoint of OP.
4. With x as centre and xO or XP as radius draw circle C₂ to cut circle C₁ at A and B.
5. Join PA and PB.
PA and PB are the tangents to the circle from P.
P\(\hat{A}\)O = 90° (Angle in a semicircle)
∴ PA ⊥ radius OA.
∴ PA is a tangent to the circle.

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution :

Steps of construction:
1. With O as centre and 4 cm as radius draw circle C₁.
2. With O as centre and 6 cm as radius draw circle C₂.
3. Take a point P on circle C₂.
4. Draw the perpendicular bisector of OP. Let x be the midpoint of OP.
5. With x as centre and xO or xP as radius draw circle C₃ to cut circle C₁ at A and B.
Join PA. PA is the tangent to circle C₁ from P.
O\(\hat{A}\)P = 90° (Angle in the semicircle)
∴ Radius OA ⊥ AP.
Hence PA is a tangent ∴ PA = 4.5 cm.
Verification by calculation:
In ΔOAP, O\(\hat{A}\)P = 90°. OA = 4 cm, OP = 6 cm.
OA² + AP² = OP²
4² + AP² = 6²
AP² = 6² – 4²
= (6 + 4) (6 – 4)
= 10 × 2 = 20
AP = \(\sqrt{20}\)
= \(\sqrt{4 \times 5}\) = 2\(\sqrt{5}\)
= 2 × 2.3 = 4.6 cm.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution :

Steps of construction:
1. Draw circle C₁ with centre O and radius = 3 cm.
2. Take a diameter LM in the circle.
3. Take a point P to the left of O at a distance of 7 cm.
4. Take a point Q to the right of O at a distance of 7 cm.
5. From P draw a tangent PS to C₁.
6. From Q draw a tangent RQ to C₂.
PS and RQ are tangents drawn to the circle from points P and Q respectively.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution :

B\(\hat{A}\)O = 60°
∴ B\(\hat{A}\)C = 180° – 60° = 120°
Steps of construction:
1. Draw a circle of radius 5 cm with centre O.
2. At O make an angle BC = 120°.
3. At B and C draw perpendiculars to the radii OB and OC.
4. Let the perpendiculars meet at A.
AB and AC are tangents drawn to the circle from A such that the angle between them is 60°.

Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution :
AC and AD are tangents, drawn from centre A to C₂.
BE and BF are tangents drawn from centre B to C₁.
AC = AD = 7.2 cm, BE = BF = 6.8 cm.
Steps of construction:
1. Draw a line segment AB – 8 cm.
2. With A as centre and radius 4 cm draw circle C₁.
3. With B as centre and radius 3 cm draw circle C₂.

4. Draw the perpendicular bisector of AB. Let x be the midpoint of AB.
5. With x as centre and radius xA or xB draw circle C₃.
6. Let it cut C, at E and F and cut C₂ at C and D.
7. Join AC, AD, BE, BF.
AC and AD are tangents drawn from A, the centre of circle C₁ to circle C₂.
BE and BF are tangents drawn from B, the centre of circle C₂ to circle C₁.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution :

Steps of construction:
1. Construct ΔABC given AB = 6 cm, BC = 8 cm, A\(\hat{B}\)C = 90°.
2. From B draw perpendicular BD to AC.
3. Let O be the midpoint of BC.
4. With O as centre and OB or OC as radius, draw C₁ to pass through B, D and C.
5. Join AO.
6. Draw its perpendicular bisector. Let x be the midpoint of AO.
7. With x as centre and xA or xO as radius, draw circle C₂. Let it cut C₁ at E and B.
8. Join AE. AB is already joined.
AB and AE are tangents to circle C₁ from A.
AE = AB = 6 cm.

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution :

A circle is drawn keeping the bangle on the paper. We have to find its centre.
Draw any two chords AB and CD in it.
Draw their perpendicular bisectors. The point of intersection O of these bisectors gives the centre of the circle.
(The perpendicular bisector of a chord passes through the centre).
Let P be the external point. Join PO. Draw the perpendicular bisector of PO. Let x be the midpoint.
With x as centre and xO or xP as radius draw circle C₂. Let it cut circle C₁ at Q and R.
Join PQ and PR. These are the tangents to the circle C₁.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 13 Surface Areas and Volumes Exercise 13.1

Unless stated otherwise, take π = \(\frac{22}{7}\)

Question 1.
Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Solution:
Volume of the cube = a³ = 64 cm³
Side of the cube \(\sqrt[3]{64}\) = a = 4 cm.

Surface area of the cuboid = 2(lb + bh + lh)
= 2[(8 × 4) + (4 × 4) + (8 × 4)]
= 2[32 + 16 + 32]
= 2 × 80
= 160 cm².

Question 2.
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:

π = \(\frac{22}{7}\), radius of the hemisphere = 7 cm,
height of the hemisphere = 7 cm,
height of the cylinder, h = 13 – 7 = 6 cm.
Inner area of the vessel = Inner area of the hemisphere vessel + Inner area of the cylinder
= 2πr² + 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 7 + 2 × \(\frac{22}{7}\) × 7 × 6
= 2 × 22 × 7+2 × 22 × 6
= 2 × 22(7 + 6)
= 44 × 13 = 572 cm².

Question 3.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:

π = \(\frac{22}{7}\), r = 3.5, l = ?
Total surface area of the toy = C.S.A. of the cone + C.S.A. of the hemisphere
= πrl + 2πr²
lv = r² + h²
= (3.5)² + (12)²
= 12.25 + 144
= 156.25
l = \(\sqrt{156.25}\)
= 12.5 cm.

h = Ax – Ox
= 15.5 – 3.5
= 12 cm.

Surface area of the toy = πrl + 2πr²
= \(\frac{22}{7}\) × 3.5 × 12.5 + 2 × \(\frac{22}{7}\) × 3.5 × 3.5
= \(\frac{22}{7}\) × 3.5[12.5 + 2 × 3.5]
= 22 × 0.5[12.5 + 7]
= 11[12.5 + 7]
= 11 × 19.5 = 214.5 cm².

Question 4.
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Solution:

Greatest diameter = 7 cm.
Surface area of the block = T.S.A. of the cube – Base area of the hemisphere + C.S.A. of the hemisphere
= 6 × 72 – πr² + 2πr²
= 6 × 49 + πr²
= 6 × 49 + \(\frac{22}{7}\) × 3.5 × 3.5
= 294 + 11 × 3.5
= 294 + 38.5
= 332.5 cm².

Question 5.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Solution:

Surface area of the remaining solid = Surface area of the cube + Surface area of the hemisphere
= 6l² + 2πr²
= 6l² + 2π\(\left(\frac{l}{2}\right)^2\)
= 6l² + 2π\(\frac{l^2}{4}=\frac{l^2}{4}\)(24 + 2π) sq. units.

Question 6.
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
Solution:

Height of the cylindrical portion = 14 – 2.5 – 2.5 = 9m = h
r = 2.5 m.
Surface area of the capsule = Surface area of the cylindrical portion + Areas of the hemispherical regions
= 2πrh + 2πr² + 2πr²
= 2πr(h + r + r)
= 2 × \(\frac{22}{7}\) × 2.5 (9 + 2.5 + 2.5)
= 2 × \(\frac{22}{7}\) × 2.5 (9 + 5)
=2× \(\frac{22}{7}\) × 2.5 × 14
= 44 × 5
= 220 mm².

Question 7.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs. 500 per m². (Note that the base of the tent will not be covered with canvas.)
Solution:
r = \(\frac{4}{2}\) = 2m, h = 2.1, l = 2.8

Area of the canvas used = C.S.A. of the cylindrical portion + C.S.A. of the conical region
= 2πrh + πrl
= πr(2h + l)
= \(\frac{22}{7}\) × 2(2 × 2.1 + 2.8)
= \(\frac{22}{7}\) × 2(4.2 + 2.8)
= \(\frac{22}{7}\) × 2 × 7
= 44 m².
Cost of the canvas = Area × Rate
= 44 × 500
= Rs. 22000.

Question 8.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².
Solution:
Height of conical part = Height of cylindrical part h = 2.4 cm.
Diameter of cylindrical part = 1.4 cm, so, the radius of cylindrical part r = 0.7 cm

Slant height of cylindrical part l = \(\sqrt{r^2+h^2}\)
= \(\sqrt{(0.7)^2+(2.4)^2}\)
= \(\sqrt{0.49+5.76}\)
= \(\sqrt{6.25}\)
= 2.5
The total surface area of the remaining solid = CSA of cylindrical part + CSA of conical part + Area of base of cylinder
= 2πrh + πrl + πr²
= 2 × \(\frac{22}{7}\) × 0.7 × 2.4 + \(\frac{22}{7}\) × 0.7 × 2.5 + \(\frac{22}{7}\) × 0.7 × 0.7
= 4.4 × 2.4 + 2.2 × 2.5 + 2.2 × 0.7
= 10.56 + 5.50 + 1.56
= 17.60 cm².

Question 9.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
Solution:

Total surface area of the article = C.S.A. of the cylinder + Surface area of the hemisphere at the top + Surface area of the hemisphere at the bottom
= 2πrh + 2πr² + 2πr²
= 2πr(h + r + r)
= 2 × \(\frac{22}{7}\) × 3.5 (10 + 3.5 + 3.5)
= 2 × 22 × 0.5 × 17
= 22 × l × 17
= 374 cm².

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 Constructions Exercise 11.1

In each of the following, give the justification of the construction also:

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Solution :

Steps of construction:
1. Draw the line segment AB = 7.6 cm.
2. At A, below AB, make an angle BAx = 30°.
3. At B, above AB, make an angle ABy = 30°.
B\(\hat{A}\)x = A\(\hat{B}\)y = 30°
These are alternate angles. ∴ Ax || By.
4. With a convenient radius cut off five equal parts
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ in Ax.
5. With the same radius cut off eight equal parts.
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈.
6. Join A₅B₈. Let it cut AB at C.
AC : CB = 5 : 8.

In ΔACA₅ and CBB₈
1. A\(\hat{C}\)A₅ = B\(\hat{C}\)B₈ (V.O.A.)
2. C\(\hat{A}\)A₅ = A\(\hat{B}\)B₈ (Alternate angles)
3. C\(\hat{A}\)₅A = B\(\hat{B}\)₈C (Alternate angles)
Δs are equiangular.
∴\(\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{\mathrm{CA}_5}{\mathrm{AB}_8}=\frac{\mathrm{CA}}{\mathrm{BC}}\)
∴ \(\frac{\mathrm{CA}}{\mathrm{BC}}=\frac{\mathrm{AA}_5}{\mathrm{BB}_8}=\frac{5}{8}\)

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.
Solution :

Steps of construction:

1. Construct ΔABC given AB = 4 cm, BC = 5 cm, AC = cm.
2. At B, make an acute angle CBx.
3. Divide Bx into three equal parts with a convenient radius.
4. Join B₃C.
5. From B₂ draw a parallel to B₃C.
6. Let it cut BC at C’.
7. At C’ make angle A’C’B = ACB.

Join A’C’.
∴ ΔABC ||| A’BC’.

In ΔABC and ΔA’BC’,
1.A\(\hat{B}\)C = A’\(\hat{B}\)C’ (Common angle)
2. A\(\hat{C}\)B = A’\(\hat{C’}\)B (Corresponding angles)
3. B\(\hat{A}\)C = B\(\hat{A’}\)C’ (Remaining angles)
Δs are equiangular.
∴ \(\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{BC} \mathrm{C}^{\prime}}\) = \(\frac{3}{2}\) ∴ [latex]\frac{BC’}{BC}=\frac{2}{3}[/latex]

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac{7}{5}\) of the corresponding sides of the first triangle.
Solution :
Steps of construction:

1. Construct a triangle ABC given BC= 7 cm, AB = 5 cm, AC = 6 cm.
2. At B, below BC, make an acute angle CBx.
3. With a convenient radius cut off seven equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
4. Join B₅C.
5. From B₁ draw a parallel to B₅C to cut BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

A’BC’ is the required triangle.
In ΔABC and ΔA’BC’

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution :

Steps of construction:

1. Draw a line segment BC = 8 cm.
2. Draw its perpendicular bisector.
3. Cut off DA = 4 cm. (altitude given)
4. Join AB and AC. ABC is the required triangle.
5. At B, below BC, draw an acute angle CBx.
6. With a convenient radius cut off three equal parts BB₁ = B₁B₂ = B₂B₃.
7. Join B₂C.
8. At B₃ draw a parallel to B₂C to meet BC extended at C’.
9. At C’ draw a parallel to CA to meet BA produced at A’.
10. Join A’C’. A’BC’ is the required triangle similar to ΔABC.

In ΔA’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C (Common angle)
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. A’\(\hat{C}\)‘B = A\(\hat{C}\)B
Δs are equiangular.
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{C}^{\prime}}{\mathrm{AC}}=\frac{\mathrm{BC}}{\mathrm{BC}}=\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}\)
\(\frac{BC’}{BC}\) = \(\frac{3}{2}\)
BC = 8 cm, BC’ = 8 × \(\frac{3}{2}\) = 12 cm.
BA = CA = 5.6 cm ∴ A’B = A’C’ = 5.6 × \(\frac{3}{2}\) = 8.4 cm.

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of the triangle ABC.
Solution :

Steps of construction:

1. Construct ΔABC given BC = 6 cm, AB = 5 cm, A\(\hat{B}\)C = 60°.
2. At B, below BC, make an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. Join B₄C.
5. From B₃ draw a parallel to B₄C to meet BC at C’.
6. At C’ draw a parallel to CA to meet CA at A’.

A’BC’ is the required triangle similar to ΔABC.
In Δs A’BC’ and ABC

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{4}{3}\) times the corresponding sides of ΔABC.
Solution :

\(\hat{A}\) + \(\hat{B}\) + \(\hat{C}\) = 180°
\(\hat{A}\) + \(\hat{B}\) = 150° (105° + 45°)
∴ \(\hat{C}\) = 30°
Steps of construction:
1. In ΔABC, BC = 7 cm.
\(\hat{B}\) = 45°, \(\hat{C}\) = 105°
∴ \(\hat{A}\) = 180° – 45° – 105°
= 180° – 150° = 30°.
Construct ΔABC given BC = 7 cm, \(\hat{B}\) = 45°, \(\hat{C}\) = 30°.
2. At B draw an acute angle CBx.
3. In Bx cut off four equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ with a convenient radius.
4. Join B₃C.
5. At B₄ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ make angle of 30° equal to A\(\hat{C}\)B. Let it meet BA produced at A’.
A’BC’ is the required triangle similar to ΔABC.
In ΔC’BB₄ CB₃ || C’B₄

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution :

BC’ = \(\frac{5}{3}\) × BC = \(\frac{5}{3}\) × 3 = 5 cm
BA’= \(\frac{5}{3}\) × 4 = \(\frac{20}{3}\) = 6.6 cm
A’C’ = \(\frac{5}{3}\) × 5 = \(\frac{25}{3}\) = 8.3 cm.

Steps of construction:

1. Construct ΔABC given BC= 3 cm, \(\hat{B}\) = 90°, BA = 4 cm.
2. At B, make an acute angle CBx.
3. Cut off five equal parts BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ along Bx with a convenient radius.
4. Join B₃C.
5. At B₅ draw a parallel to B₃C to meet BC produced at C’.
6. At C’ draw a parallel to CA to meet BA produced at A’.

A’BC’ is the required triangle similar to ΔABC.
BC’ : BC = BB₅ = BB₃
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{BB}_5}{\mathrm{BB}_3}\) = \(\frac{5}{3}\)

In Δs A’BC’ and ABC
1. A’\(\hat{B}\)C’ = A\(\hat{B}\)C = 90°
2. B\(\hat{A}\)‘C’ = B\(\hat{A}\)C (Corresponding angles)
3. B\(\hat{C}\)‘A’ = B\(\hat{C}\)A
Δs are equiangular.
∴ \(\frac{A’C’}{AC}\) = \(\frac{BC’}{BC}\) = \(\frac{BA’}{BA}\) = \(\frac{5}{3}\)

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 Statistics Exercise 14.4

Question 1.
The following distribution gives the daily income of 50 workers of a factory:

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:

Question 2.
During the medical check-up of 35 students of a class, their weights were recorded as follows:

Weight (in kg)	No. of students
Less than 38	0
Less than 40	3
Less than 42	5
Less than 44	9
Less than 46	14
Less than 48	28
Less than 50	32
Less than 52	35

Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:

Weight (in kg)	Frequency	Cumulative frequency
36 – 38	0	0
38 – 40	3	3
40 – 42	2	5
42 – 44	4	9
44 – 46	5	14 = cf
46 – 48	14 = f	28
48 – 50	4	32
50 – 52	3	35
	n = 35

\(\frac{\mathrm{n}}{2}=\frac{35}{2}=17.5\)
Plot the points (38, 0) (40, 3) (42, 5) (44, 9) (46, 14) (48, 28) (50, 32) (52, 35)
Median = l + \(\left[\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\right]\) × h
= 46 + \(\left[\frac{17.5-14}{14}\right]\) × 2
= 46 + \(\frac{3.5 \times 2}{14}\)
= 46 + 0.5= 46.5.

Question 3.
The following table gives production yield per hectare of wheat of 100 farms of a village:

Change the distribution to a more than type distribution, and draw its ogive.
Solution:

Production yield (in kg/hec)	Number of farms	c.f.
More than 50	2	100
More than 55	8	98
More than 60	12	90
More than 65	24	78
More than 70	38	54
More than 75	16	16

∴ Co-ordinate points are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16).

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 Statistics Exercise 14.3

Question 1.
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the media, mean and mode of the data and compare them.

Monthly consumption (in units)	No. of consumers
65 – 85	4
85 – 105	5
105 – 125	13
125 – 145	20
145 – 165	14
165 – 185	8
185 – 205	4

Solution:


Mean is 137 units.
Median is 137 units.
Mode is 135.76 units.
The three measures are approximately the same.

Question 2.
If the median of the distribution given below is 28.5, find the values of x and y.

Class interval	Frequency
0 – 10	5
10 – 20	x
20 – 30	20
30 – 40	15
40 – 50	y
50 – 60	5
Total	60

Solution:

Class interval	Frequency	Cumulative frequency
0 – 10	5	5
10 – 20	x	5 + x
20 – 30	20	25 + x
30 – 40	15	40 + x
40 – 50	y	40 + x + y
50 – 60	5	45 + x + y
	60

n = 60, 45 + x + y = 60
x + y = 60 – 45
x + y = 15
The median is 28.5. It lies in the class interval 20 – 30.
∴ l = 20, f = 20, cf = 5 + x, h = 10

Question 3.
A life insurance agent found the following data for distribution of ages of 100 policyholders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.

Age (in years)	No. of policyholders
Below 20	2
Below 25	6
Below 30	24
Below 35	45
Below 40	78
Below 45	89
Below 50	92
Below 55	98
Below 60	100

Solution:

Class interval	No. of policyholders	c.f.
Below 20	2	2
20 – 25	4	6
25 – 30	18	24
30 – 35	21	45
35 – 40	33	78
40 – 45	11	89
45 – 50	3	92
50 – 55	6	98
55 – 60	2	100
	n = 100	\(\frac{n}{2}\) = 50

l = 35, \(\frac{n}{2}\) = 50, cf = 45, f = 33, h = 5

Question 4.
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table:

Length (in mm)	Number of leaves
118 – 126	3
127 – 135	5
136 – 144	9
145 – 153	12
154 – 162	5
163 – 171	4
172 – 180	2

Find the median length of the leaves.
(Hint: The data need to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 – 126.5, 126.5 – 135.5, ….., 171.5 – 180.5).
Solution:
The data have to be converted to continuous classes for finding the median since the formula. assumes continuous classes.

Class interval	No. of leaves	Cumulative frequency (cf)
117.5 – 126.5	3	3
126.5 – 135.5	5	8
135.5 – 144.5	9	17
144.5 – 153.5	12	29
153.5 – 162.5	5	34
162.5 – 171.5	4	38
171.5 – 180.5	2	40

n = 40, \(\frac{n}{2}\) = 20
The median lies in the class interval 144.5 – 153.5.
l = 144.5, \(\frac{\mathrm{n}}{2}=\frac{40}{2}\) = 20, cf = 17, f = 12, h = 9.
Median = l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
= 144.5 + \(\left[\frac{20-17}{12} \times 9\right]\)
= 144.5 + \(\left[\frac{27}{12}\right]\)
= 144.5 + 2.25
= 146.75 mm.

Question 5.
The following table gives the distribution of the lifetime of 400 neon lamps:

Lifetime (in hours)	Number of lamps
1500 – 2000	14
2000 – 2500	56
2500 – 3000	60
3000 – 3500	86
3500 – 4000	74
4000 – 4500	62
4500 – 5000	48

Find the median lifetime of a lamp.
Solution:

Lifetime in hours (CI)	No. of lamps (l)	Cumulative frequency
1500 – 2000	14	14
2000 – 2500	56	70
2500 – 3000	60	130
3000 – 3500	86	216
3500 – 4000	74	290
4000 – 4500	62	352
4500 – 5000	48	400

The median lies in the class interval 3000 – 3500.
\(\frac{\mathrm{n}}{2}=\frac{400}{2}=200\)
l = 3000, \(\frac{n}{2}\) = 200, cf = 130, f = 86, h = 500.
Median = l + \(\left[\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\right]\) × h
= 3000 + \(\left[\frac{200-130}{86}\right]\) × 500
= 3000 + \(\left[\frac{70}{86}\right]\) × 500
= 3000 + \(\frac{35000}{86}\)
= 3000 + 406.976
Median life of a lamp is 3406.98 hours.

Question 6.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabet in the surnames was obtained as follows:

No. of letters	No. of surnames
1 – 4	6
4 – 7	30
7 – 10	40
10 – 13	16
13 – 16	4
16 – 19	4

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames.
Solution:

Hence the modal size of the surnames is 7.88.

Question 7.
The distribution below gives the weights of 30 students of a class. Find the median weight of the students.

Solution:

Weight in kg.	No. of students	Cumulative frequency (c.f.)
40 – 45	2	2
45 – 50	3	5
50 – 55	8	13
55 – 60	6	19
60 – 65	6	25
65 – 70	3	28
70 – 75	2	30

\(\frac{n}{2}\) = 15
The median lies in the class 55 – 60.
l = 55, \(\frac{n}{2}\) = 15, c.f. = 13, f = 6, h = 5.
Median = l + \(\frac{1}{2}\) × h
= 55 + \(\left[\frac{15-13}{6}\right]\) × 5
= 55 + \(\frac{2}{6}\) × 5
= 55 + \(\frac{5}{3}\)
= 55 + 1.666 = 56.666
∴ Median = 56.67 kg.
Hence, the median weight of the students is 56.67 kg.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 10 Circles Ex 10.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 10 Circles Exercise 10.2

Question 1.
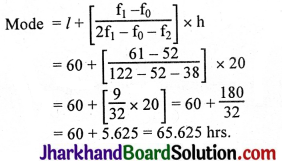
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Solution :

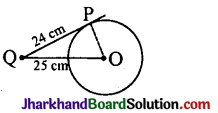
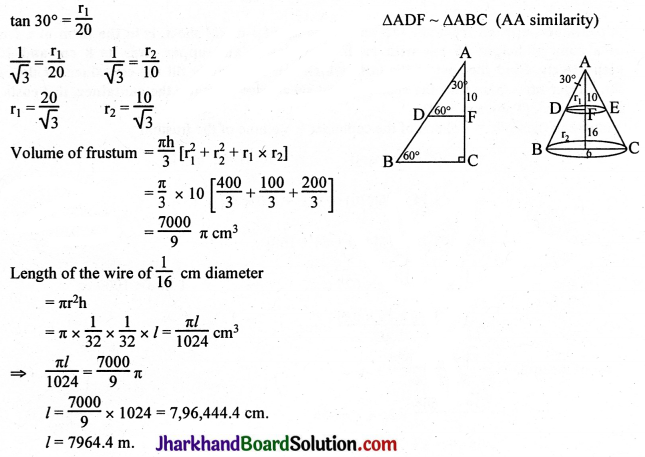
OQ² = TO² – TQ²
= 25² – 24²
= (25 + 24) (25 – 24)
= 49 × 1 = 49
OQ = \(\sqrt{49}\) = 7 cm.

Question 2.
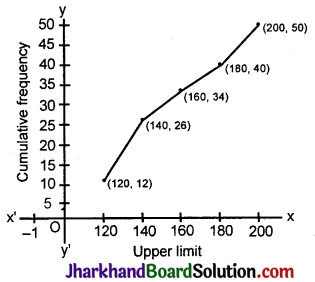
In the figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Solution :

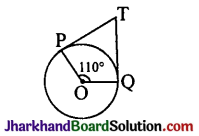
POQT is a cyclic quadrilateral because \(\hat{\mathbf{P}}\) + \(\hat{\mathbf{O}}\) = 180°.
∴ \(\hat{\mathbf{O}}\) + \(\hat{\mathbf{T}}\) = 180°
latex]\hat{\mathbf{O}}[/latex] = 110°.
latex]\hat{\mathbf{T}}[/latex] = 180° – 110° = 70°.

Question 3.
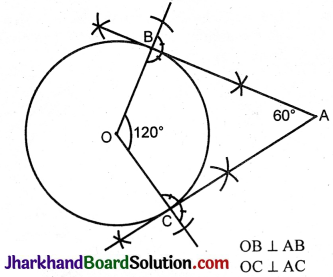
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to

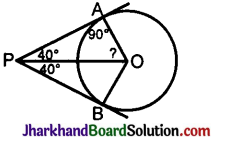
A) 50°
B) 60°
C) 70°
D) 80°
Solution :
In ΔPAO, P\(\hat{A}\)O = 90° A\(\hat{P}\)O = 40°
∴ A\(\hat{O}\)P = 180° – 90° – 40° = 50°.

Question 4.
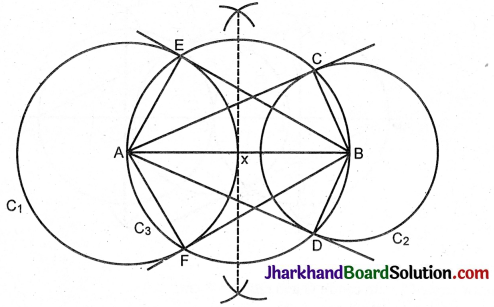
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution :

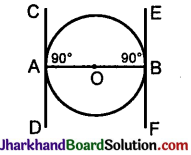
Data: O is the centre of the circle.
AB is a diameter. CD and EF are tangents drawn at A and B.
To prove: CD || EF.
Proof: O\(\hat{A}\)C = 90°
O\(\hat{B}\)E = 90°
B\(\hat{A}\)C + A\(\hat{B}\)E = 180°
These are co-interior angles.
Radius is ⊥ to the tangent at the point of contact

Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution :

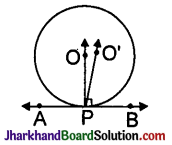
Let us consider a circle with centre O.
Let AB be a tangent which touches the circle at P.
We have to prove that the line perpendicular to AB at P passes through the centre O.
We shall prove this by contradiction method.
Let us assume that the perpendicular to AB at P does not pass through centre O.
Let it pass through another point O’. Join OP and O’P.
As the perpendicular to AB at P passes through O’, therefore,
∠O’PB = 90° ……..(1)
O is the centre of the circle and P is the point of contact. We know that the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
∴ ∠OPB = 90° ……..(2)
Comparing equations (1) and (2), we obtain
∠O’PB = ∠OPB ….(3)
From the figure, it can be observed that,
∠O’PB < ∠OPB ………..(4)
Therefore, ∠O’PB = ∠OPB is not possible. It is only possible when the line O’P coincides with OP. Therefore, the perpendicular to AB at P passes through the centre O.

Question 6.
The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

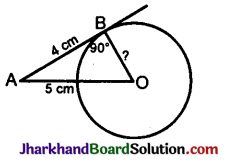
Solution :
A\(\hat{B}\)O = 90° (The radius is perpendicular to the tangent at the point of contact)
BO² + AB² = AO²
BO² = AO² – AB²
= 5² – 4²
= 25 – 16 = 9
BO = \(\sqrt{9}\) = 3 cm.
Hence, radius of the circle is 3 cm.

Question 7.
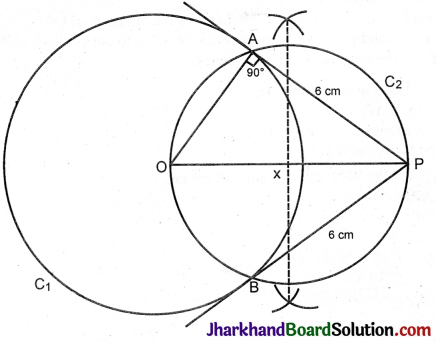
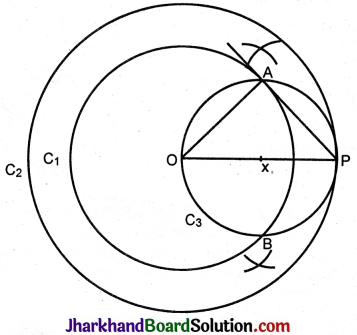
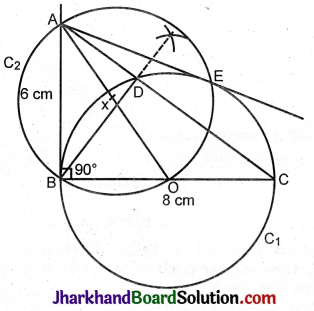
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution :

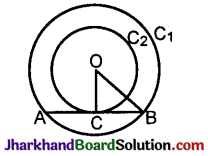
O is the centre of the concentric circles C₁ and C₂.
AB is a chord of the bigger circle C₁.
AB is a tangent to circle C₂.
OC = 3 cm, OB = 5 cm.
To find AB.
Proof: In ΔOCB,
O\(\hat{C}\)B = 90° (The tangent AB to C₂ is ⊥ to the radius CO drawn from the point of contact C)
In ΔOCB, O\(\hat{C}\)B = 90°
OC² + CB² = OB²
3² + CB² = 5²
CB² = 5² – 3²
= 25 – 9 = 16
CB = 4 cm.
In circle C₁ AB is a chord. OC ⊥ AB.
∴ AC = CB = 4 cm. The ⊥ drawn to a chord from the centre bisects the chord.
AB = AC + CB
= 4 + 4 = 8 cm.

Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
Solution :

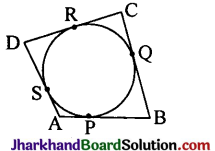
A, B, C and D are external points. Tangents drawn to the circle from these points are equal.
AP = AS ….(1) (Tangents from A)
BP = BQ ….(2) (Tangents from B)
CR = CQ ….(3) (Tangents from C)
DR = DS ….(4) (Tangents from D)
Adding the results
AP + BP + CR + DR = AS + BQ+CQ + DS
AB + CD = AS + DS + BQ +CQ
∴ AB + CD = AD + BC.

Question 9.
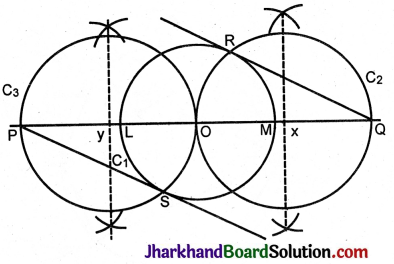
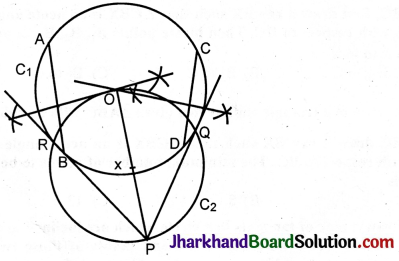
In the figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
Solution :

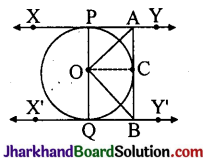
Given: XY || X’Y’.
XPA, X’QY’ and AB are the tangents.
To prove: ∠AOB = 90°
Construction: Join OC.
Proof: In ΔOAP and ΔOAC
AP = AC (Theorem 4.2)
OA = OA (Common)
OP = OC (Radii of circle)
AOAP AOAC (S.S.S. congruency)
Since XY || X’Y’
∠PAB + ∠QBA = 180° (Co-interior angles)
\(\frac{1}{2}\)∠PAB + \(\frac{1}{2}\)∠QBA = 90°
∴ ∠OAB + ∠OBA = 90°
In ΔAOB, ∠AOB = 180° – (∠OAB + ∠OBA)
= 180° – 90° = 90°
∴ ∠AOB = 90°.
The line joining the external point to the centre, bisects the angle between the tangents.

Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Solution :

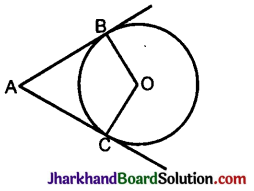
Data: O is the centre of the circle.
AB and AC are tangents drawn from A.
To prove: B\(\hat{\mathbf{A}}\)C + B\(\hat{\mathbf{O}}\)C = 180°.
Proof: AB is a tangent. BO is the radius drawn from the point of contact B.
∴ O\(\hat{\mathbf{B}}\)A = 90°
AC is a tangent. CO is the radius drawn from the point of contact C.
∴ O\(\hat{\mathbf{C}}\)A = 90°
∴ O\(\hat{\mathbf{B}}\)A + O\(\hat{\mathbf{C}}\)A = 90°.
∴ B\(\hat{\mathbf{O}}\)C + B\(\hat{\mathbf{A}}\)C = 180° [Sum of angles of a quadrilateral is 360°]

Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution :

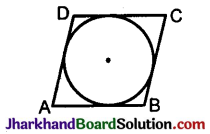
Data: ABCD is a circumscribed parallelogram.
AB = CD, AD = BC
To prove: ABCD is a rhombus.
AB = BC – CD – DA
Proof: ABCD is a circumscribed quadrilateral.
∴ AB + CD = AD + BC (Proved in problem 8)
AB = DC, AD = BC (Opposite sides of the parallelogram)
AB + AB = AD + AD
2AB = 2AD
AB = AD
AB = CD, AD = BC
AB = BC = CD = DA. [Since adjacent sides of a parallelogram are equal]
∴ ABCD is a rhombus.

Question 12.
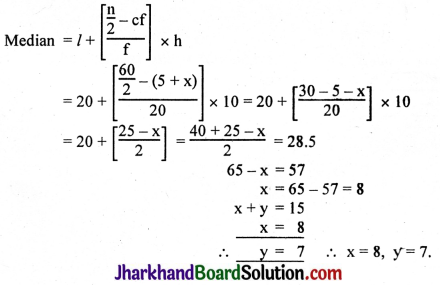
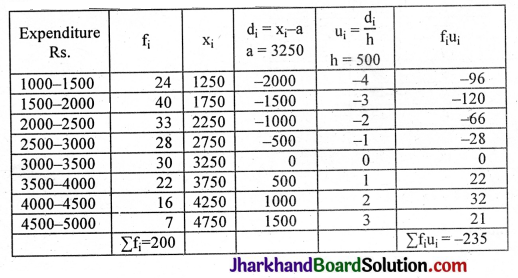
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.

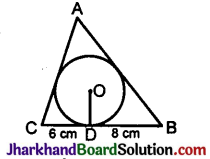
Solution :

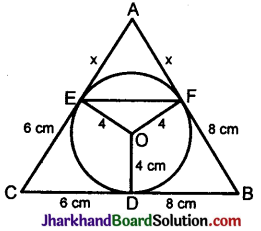
In the adjoining figure, the circle touches AB at F, BC at D, CA at E.
AE = AF = x. (Tangents to the circle from A)
Tangent BF = Tangent BD = 8 cm
Tangent CE = Tangent CD = 6 cm
AB = AF + FB = (x + 8) cm
AC = AE + EC = (x + 6) cm
CB = CD + DB = 6 + 8 = 14 cm.
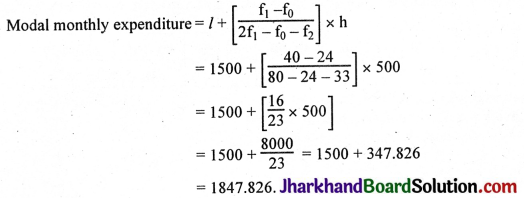
2S(perimeter of AABC) = AB + BC + CA
= (x + 8) + (6 + 8) + (x + 6).
= 2x + 28
S = x + 14

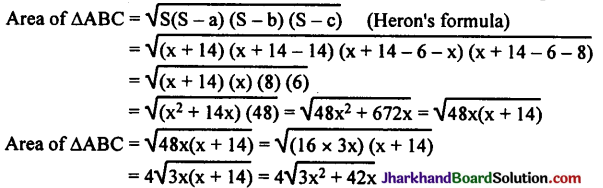
Area of ΔABC = \(\frac{1}{2}\) × base × altitude
= \(\frac{1}{2}\) × 14 × 4 = 28 cm².
Area of ΔOAB = \(\frac{1}{2}\) × 4(x + 8) = 2(x + 8)
Area of ΔOAC = \(\frac{1}{2}\) × 4(x + 6) = 2(x + 6)
Area of ΔOBC = \(\frac{1}{2}\) × 4 × 14 = 28 cm.
Total area = Area of ΔOBC + Area of ΔOAB + Area of ΔOAC
= 28 + 2x + 12 + 2x + 16
∴ 4x + 56 = 4(x + 14)
∴ 4\(\sqrt{3 x^2+42 x}\) = 4(x + 14)
\(\sqrt{3 x^2+42 x}\) = x + 14
Squaring both sides 3x² + 42x = (x + 14)² = x² + 28x + 196
= 2x² + 145 – 196 = 0 x² + 7x – 98 = 0
∴ (x + 14) (x – 7) = 0 x = – 14 or x = 7
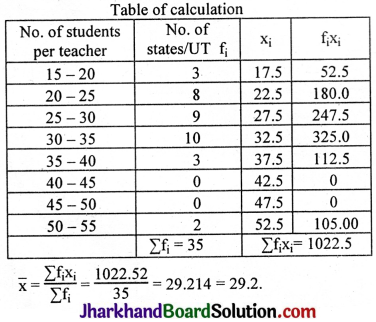
AC = x + 8
= 7 + 8
= 15 cm.

AC = x + 6
= 7 + 6
= 13 cm.

BC = 6 + 8
= 14 cm.

Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution :

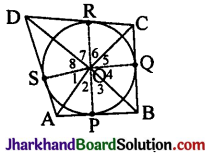
Construction: Join OP, OQ, OR and OS.
Proof: The two tangents drawn from an external point to a circle subtend equal angles at the centre.
∴ ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8.
Now, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360° (Sum of angles subtended at a point)
2(∠2 + ∠3 + ∠6 + ∠7) = 360° and
2(∠1 + ∠8 + ∠4 + ∠5) = 360°
⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180°
(∠1 + ∠8) + (∠4 + ∠5) = 180°
∴ ∠AOB + ∠COD = 180° and ∠AOD + ∠BOC = 180°.

Jharkhand Board JAC Class 10 Maths Solutions Chapter 14 Statistics Ex 14.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 14 Statistics Exercise 14.2

Question 1.
The following table shows the ages of the patients admitted in a hospital during a year:

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:
The class interval having the maximum frequencies is 35 – 45.
f₁ = 23, l = 35, h = 10, f₀ = 21, f₂ = 14


Maximum number of patients admitted in the hospital are of the age 36.8 years. The average age of the patient admitted to the hospital is 35.37 years.

Question 2.
The following data gives the information on the observed lifetimes (in hours) of 225 electrical

Determine the modal lifetimes of the components.
Class interval having the maximum frequency is 60 – 80.
f₁ = 61, f₀ = 52, f₂ = 38, l = 60, h = 20.

Question 3.
The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:

Expenditure (in Rs.)	No. of families
1000 – 1500	24
1500 – 2000	40
2000 – 2500	33
2500 – 3000	28
3000 – 3500	30
3500 – 4000	22
4000 – 4500	16
4500 – 5000	7

Solution:

Step deviation method: \(\bar{x}\) = a + \(\left[\frac{\sum f_i u_i}{\sum f_i}\right]\)h
= 3250 + \(\left[\frac{-235}{200}\right]\) × 500
= 3250 – \(\left[-\frac{1175}{2}\right]\)
= 3250 – 587.5
= 2662.5.
Mean expenditure Rs. 2662.50.
l = 1500, f₁ = 40, f₂ = 33, f₀ = 24, h = 500

Modal monthly expenditure = 1847.83.

Question 4.
The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.

Number of students per teacher	No. of states/U.T.
15 – 20	3
20 – 25	8
25 – 30	9
30 – 35	10
35 – 40	3
40 – 45	0
45 – 50	0
50 – 55	2

Solution:

l = lower limit of the CI = 30, f₁ = 10, f₀ = 9, f₂ = 3, h = 5
Mode = \(l+\left[\frac{\mathrm{f}_1-\mathrm{f}_0}{2 \mathrm{f}_1-\mathrm{f}_0-\mathrm{f}_2}\right] \times \mathrm{h}\)
= \(=30+\left[\frac{10-9}{20-9-3}\right] \times 5\)
= \(30+\left[\frac{1}{8} \times 5\right]=30+\frac{5}{8}\)
= 30 + 0.625 = 30.625.
Most states/UT’s have a student-teacher ratio of 30.6. On an average this ratio is 29.2.

Question 5.
The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.

Runs scored	Number of batsmen
3000 – 4000	4
4000 – 5000	18
5000 – 6000	9
6000 – 7000	7
7000 – 8000	6
8000 – 9000	3
9000 – 10000	1
10000 – 11000	1

Find the mode of the data.
Solution:
l = 4000, f₁ = 18, f₀ = 4, f₂ = 9, h = 1000

Question 6.
A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data.

Solution:
Class interval having the maximum frequency is 40 – 50. f₁ = 20, f₀ = 12, f₂ = 11, l = 40, h = 10.