Month: September 2022

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.4

Question 1.
Visualise 3.765 on the number line using successive magnification.
Answer:

Question 2.
Visualize 4.26 on the number line, up to 4 decimal places.
Answer:
\(4 . \overline{26}\) = 4.2626…

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.3 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.3

Question 1.
Write the following in decimal form and say what kind of decimal expansion each has:
(i) \(\frac{36}{100}\)
(ii) \(\frac{1}{11}\)
(iii) \(4 \frac{1}{8}\)
(iv) \(\frac{3}{13}\)
(v) \(\frac{2}{11}\)
(vi) \(\frac{329}{400}\)
Answer:
(i) \(\frac{36}{100}\) = 0.36 (Terminating)

(ii) \(\frac{1}{11}\) = 0.09090909… = \(0 . \overline{09}\) (Non-terminating and repeating)

(iii) \(4 \frac{1}{8}\) = \(\frac{33}{8}\) =4.125 (Terminating)

(iv) \(\frac{3}{13}\) = 0.230769230769… = \(0 . \overline{230769}\) (Non-terminating and repeating)

(v) \(\frac{2}{11}\) = 0.181818181818… = \(0 . \overline{18}\) (Non-terminating and repeating)

(vi) \(\frac{329}{400}\) = 0.8225 (Terminating)

Question 2.
You know that \(\frac{1}{7}\) = 0.142857. Can you predict what the decimal expansion of \(\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) are without actually doing the long division? If so, how?
[Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully.]
Answer:
Yes, We can do this by:

\(\frac{2}{7}=2 \times \frac{1}{7}=2 \times 0 . \overline{142857}=0 . \overline{285714}\)
\(\frac{3}{7}=3 \times \frac{1}{7}=3 \times 0 . \overline{142857}=0 . \overline{428571}\)
\(\frac{4}{7}=4 \times \frac{1}{7}=4 \times 0 . \overline{142857}=0 . \overline{571428}\)
\(\frac{5}{7}=5 \times \frac{1}{7}=5 \times 0 . \overline{142857}=0 . \overline{714285}\)
\(\frac{6}{7}=6 \times \frac{1}{7}=6 \times 0 . \overline{142857}=0 . \overline{857142}\)

Question 3.
Express the following in the form p/q, where p and q are integers and q ≠ 0.
(i) \(0 . \overline{6}\)
(ii) \(0 . 4 \overline{7}\)
(iii) \(0 . \overline{001}\)
Answer:
(i) \(0 . \overline{6}\) = 0.666…
Let x = 0.666…
∴ 10x = 6.66…
∴ 10x = 6 + 0.66…
∴ 10x = 6 + 0.666…
∴ 10x = 6 + x
∴ 9x = 6
x = \(\frac{2}{3}\)

(ii) \(0 . 4 \overline{7}\) = 0.4777… = \(\frac{4}{10}\) + \(\frac{0.777}{10}\)
Let x = 0.777…
∴ 10x = 7.77…
∴ 10x = 7.777…
∴ 10x = 7 + 0.777…
∴ 10x = 7 + x
∴ x = \(\frac{7}{9}\)
\(0 . 4 \overline{7}\) = \(\frac{4}{10}\) + \(\frac{0.777}{10}\) = \(\frac{4}{10}\) + \(\frac{7}{90}\)
= \(\frac{36}{90}\) + \(\frac{7}{90}\) = \(\frac{43}{90}\)

(iii) \(0 . \overline{001}\) =0.001001…
Let x = 0.001001…
∴ 1000x = 1.001….
∴ 1000x = 1.001001…
∴ 1000x = 1 + 0.001001 …
∴ l000x= 1 + X
∴ 999x = 1
x = \(\frac{1}{999}\)

Question 4.
Express 0.99999…in the form \(\frac{p}{q}\). Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Answer:
Let x = 0.9999…
10x = 9.999…
∴ 10x = 9.9999…
∴ 10x = 9 + 0.9999…
∴ 10x = 9 + x
∴ 9x = 9
x = 1
The difference between 1 and 0.999999 is 0.000001 which is negligible. Thus, 0.999… is too much near 1. Therefore, the answer 1 can be justified.

Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer.
Answer:
\(\frac{1}{17}\) = 0.05882352941176470588…
= \(0 . \overline{0588235294117647}\)
There are 16 digits in the repeating block of the decimal expansion of \(\frac{1}{17}\)

Question 6.
Look at several examples of rational numbers in the form \(\frac{p}{q}\) (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
We observe that when q is 2, 4, 5, 8, 10,… then the decimal expansion is terminating. For example:
\(\frac{1}{2}\) = 0.5, denominator q = 2¹
\(\frac{4}{5}\) = 0.8, denominator q = 5¹
We can observe that terminating decimal may be obtained in the situation where prime factorisation of the denominator of the given fractions has the power of 2 only or 5 only or both.

Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
Three numbers whose decimal expansions are non-terminating non-recurring are:
(i) 0.303003000300003…
(ii) 0.505005000500005…
(iii) 0.7207200720007200007200000…

Question 8.
Find three different irrational numbers between the rational numbers \(\frac{5}{7}\) and \(\frac{9}{11}\).
Answer:
\(\frac{5}{7}\) = \(0 . \overline{714285}\)

\(\frac{9}{11}\) = \(0 . \overline{81}\)
Three different irrational numbers are:
0.73073007300073000073…
0.75075007500075000075…
0.76076007600076000076…

Question 9.
Classify the following numbers as rational or irrational:
(i) \(\sqrt{23}\)
(ii) \(\sqrt{225}\)
(iii) 0.3796
(iv) 7.478478…
(v) 1.101001000100001…
Answer:
(i) \(\sqrt{23}\) = 4.79583152331…
Since the decimal expansion is non-terminating and non-recurring therefore, it is an irrational number.

(ii) \(\sqrt{225}\) = 15 = \(\frac{15}{1}\)
The number is rational number as it can represented in \(\frac{p}{q}\) form where p, q ∈ Z and q ≠ 0.

(iii) 0.3796
Since the decimal expansion is terminating therefore, it is a rational number.

(iv) 7.478478… = \(7 . \overline{478}\)
Since, this decimal expansion is non-terminating recurring, therefore, it is a rational number.

(v) 1.101001000100001…
Since the decimal expansion is non-terminating and non-repeating, therefore, it is an irrational number.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.2 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.2

Question 1.
State whether the following statements are true or false. Justify your Answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form \(\sqrt{m}\) , where m is a natural number.
(iii) Every real number is an irrational number.
Answer:
(i) True, since the collection of real numbers is made up of rational and irrational numbers.
(ii) False, since negative numbers cannot be expressed as square roots.
(iii) False, as real numbers include both rational and irrational numbers. Therefore, every real number cannot be an irrational number, e.g. 2 is a real number but not an irrational number.

Question 2.
Are the square roots of all positive inte-gers irrational? If not, give an example of the square root of a number that is a rational number.
Answer:
No, the square roots of all positive integers are not irrational. For example \(\sqrt{4}\) = 2, which is rational number.

Question 3.
Show how \(\sqrt{5}\) can be represented on the number line.
Answer:
Step 1: Let AB be a line segment of length 2 units on number line.
Step 2: At B, draw a perpendicular line BC of length 1 unit. Join CA.
Step 3: Now, ABC is a right angled triangle. Applying Pythagoras theorem,
AB² + BC² = CA²
⇒ 2² + 1² = CA²
⇒ CA² = 5
⇒ CA = \(\sqrt{5}\)
Thus, CA is a line of length \(\sqrt{5}\) units.

Step 4: Taking CA as a radius and A as a centre draw an arc touching the number line. The point D at which number line gets intersected by arc of length AC is at \(\sqrt{5}\) distance from 0.
Thus, \(\sqrt{5}\) is represented on the number line as shown in the figure.

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.1 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.1

Question 1.
Is zero a rational number? Can you write it in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0?
Answer:
Yes, Zero is a rational number as it can be represented as \(\frac{0}{1}\) or \(\frac{0}{2}\) and so on.

Question 2.
Find six rational numbers between 3 and 4.
Answer:
There are infinitely many rational numbers between 3 and 4.
3 and 4 can be represented as \(\frac{24}{8}\) and \(\frac{32}{8}\) respectively.
Therefore, six rational numbers between 3 and 4 are: \(\frac{25}{8}\), \(\frac{26}{8}\), \(\frac{27}{8}\), \(\frac{28}{8}\), \(\frac{29}{8}\), \(\frac{30}{8}\).

Question 3.
Find five rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\).
Answer:
There are infinitely many rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\)
\(\frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}\)
\(\frac{4}{5}=\frac{4 \times 6}{5 \times 6}=\frac{24}{30}\)
Therefore, five rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}\) are \(\frac{19}{30}\), \(\frac{20}{30}\), \(\frac{21}{30}\), \(\frac{22}{30}\), \(\frac{23}{30}\).

Question 4.
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Answer:
(i) True, since the collection of whole numbers contains all natural numbers.
(ii) False, as integers may be negative but whole numbers are always positive, e.g. – 1 is an integer but not a whole number.
(iii) False, as rational numbers may be fractional but whole numbers are not fractional, e.g. \(\frac{2}{3}\) is a rational number but not a whole number.

JAC Jharkhand Board Class 9th Maths Solutions in Hindi & English Medium

JAC Board Class 9th Maths Solutions in English Medium

JAC Class 9 Maths Chapter 1 Number Systems

• Chapter 1 Number Systems Ex 1.1
• Chapter 1 Number Systems Ex 1.2
• Chapter 1 Number Systems Ex 1.3
• Chapter 1 Number Systems Ex 1.4
• Chapter 1 Number Systems Ex 1.5
• Chapter 1 Number Systems Ex 1.6

JAC Class 9 Maths Chapter 2 Polynomials

• Chapter 2 Polynomials Ex 2.1
• Chapter 2 Polynomials Ex 2.2
• Chapter 2 Polynomials Ex 2.3
• Chapter 2 Polynomials Ex 2.4
• Chapter 2 Polynomials Ex 2.5

JAC Class 9 Maths Chapter 3 Coordinate Geometry

• Chapter 3 Coordinate Geometry Ex 3.1
• Chapter 3 Coordinate Geometry Ex 3.2
• Chapter 3 Coordinate Geometry Ex 3.3

JAC Class 9 Maths Chapter 4 Linear Equations in Two Variables

• Chapter 4 Linear Equations in Two Variables Ex 4.1
• Chapter 4 Linear Equations in Two Variables Ex 4.2
• Chapter 4 Linear Equations in Two Variables Ex 4.3
• Chapter 4 Linear Equations in Two Variables Ex 4.4

JAC Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry

• Chapter 5 Introduction to Euclid’s Geometry Ex 5.1
• Chapter 5 Introduction to Euclid’s Geometry Ex 5.2

JAC Class 9 Maths Chapter 6 Lines and Angles

• Chapter 6 Lines and Angles Ex 6.1
• Chapter 6 Lines and Angles Ex 6.2
• Chapter 6 Lines and Angles Ex 6.3

JAC Class 9 Maths Chapter 7 Triangles

• Chapter 7 Triangles Ex 7.1
• Chapter 7 Triangles Ex 7.2
• Chapter 7 Triangles Ex 7.3
• Chapter 7 Triangles Ex 7.4
• Chapter 7 Triangles Ex 7.5

JAC Class 9 Maths Chapter 8 Quadrilaterals

• Chapter 8 Quadrilaterals Ex 8.1
• Chapter 8 Quadrilaterals Ex 8.2

JAC Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles

• Chapter 9 Areas of Parallelograms and Triangles Ex 9.1
• Chapter 9 Areas of Parallelograms and Triangles Ex 9.2
• Chapter 9 Areas of Parallelograms and Triangles Ex 9.3
• Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

JAC Class 9 Maths Chapter 10 Circles

• Chapter 10 Circles Ex 10.1
• Chapter 10 Circles Ex 10.2
• Chapter 10 Circles Ex 10.3
• Chapter 10 Circles Ex 10.4
• Chapter 10 Circles Ex 10.5
• Chapter 10 Circles Ex 10.6

JAC Class 9 Maths Chapter 11 Constructions

• Chapter 11 Constructions Ex 11.1
• Chapter 11 Constructions Ex 11.2

JAC Class 9 Maths Chapter 12 Heron’s Formula

• Chapter 12 Heron’s Formula Ex 12.1
• Chapter 12 Heron’s Formula Ex 12.2

JAC Class 9 Maths Chapter 13 Surface Areas and Volumes

• Chapter 13 Surface Areas and Volumes Ex 13.1
• Chapter 13 Surface Areas and Volumes Ex 13.2
• Chapter 13 Surface Areas and Volumes Ex 13.3
• Chapter 13 Surface Areas and Volumes Ex 13.4
• Chapter 13 Surface Areas and Volumes Ex 13.5
• Chapter 13 Surface Areas and Volumes Ex 13.6
• Chapter 13 Surface Areas and Volumes Ex 13.7
• Chapter 13 Surface Areas and Volumes Ex 13.8
• Chapter 13 Surface Areas and Volumes Ex 13.9

JAC Class 9 Maths Chapter 14 Statistics

• Chapter 14 Statistics Ex 14.1
• Chapter 14 Statistics Ex 14.2
• Chapter 14 Statistics Ex 14.3
• Chapter 14 Statistics Ex 14.4

JAC Class 9 Maths Chapter 15 Probability

• Chapter 15 Probability Ex 15.1

JAC Board Class 9th Maths Solutions in Hindi Medium

JAC Class 9 Maths Chapter 1 संख्या पद्धति

• Chapter 1 संख्या पद्धति Ex 1.1
• Chapter 1 संख्या पद्धति Ex 1.2
• Chapter 1 संख्या पद्धति Ex 1.3
• Chapter 1 संख्या पद्धति Ex 1.4
• Chapter 1 संख्या पद्धति Ex 1.5
• Chapter 1 संख्या पद्धति Ex 1.6

JAC Class 9 Maths Chapter 2 बहुपद

• Chapter 2 बहुपद Ex 2.1
• Chapter 2 बहुपद Ex 2.2
• Chapter 2 बहुपद Ex 2.3
• Chapter 2 बहुपद Ex 2.4
• Chapter 2 बहुपद Ex 2.5

JAC Class 9 Maths Chapter 3 निर्देशांक ज्यामिति

• Chapter 3 निर्देशांक ज्यामिति Ex 3.1
• Chapter 3 निर्देशांक ज्यामिति Ex 3.2
• Chapter 3 निर्देशांक ज्यामिति Ex 3.3

JAC Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण

• Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1
• Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.2
• Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.3
• Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4

JAC Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय

• Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.1
• Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2

JAC Class 9 Maths Chapter 6 रेखाएँ और कोण

• Chapter 6 रेखाएँ और कोण Ex 6.1
• Chapter 6 रेखाएँ और कोण Ex 6.2
• Chapter 6 रेखाएँ और कोण Ex 6.3

JAC Class 9 Maths Chapter 7 त्रिभुज

• Chapter 7 त्रिभुज Ex 7.1
• Chapter 7 त्रिभुज Ex 7.2
• Chapter 7 त्रिभुज Ex 7.3
• Chapter 7 त्रिभुज Ex 7.4
• Chapter 7 त्रिभुज Ex 7.5

JAC Class 9 Maths Chapter 8 चतुर्भुज

• Chapter 8 चतुर्भुज Ex 8.1
• Chapter 8 चतुर्भुज Ex 8.2

JAC Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

• Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.1
• Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2
• Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3
• Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.4

JAC Class 9 Maths Chapter 10 वृत्त

• Chapter 10 वृत्त Ex 10.1
• Chapter 10 वृत्त Ex 10.2
• Chapter 10 वृत्त Ex 10.3
• Chapter 10 वृत्त Ex 10.4
• Chapter 10 वृत्त Ex 10.5
• Chapter 10 वृत्त Ex 10.6

JAC Class 9 Maths Chapter 11 रचनाएँ

• Chapter 11 रचनाएँ Ex 11.1
• Chapter 11 रचनाएँ Ex 11.2

JAC Class 9 Maths Chapter 12 हीरोन का सूत्र

• Chapter 12 हीरोन का सूत्र Ex 12.1
• Chapter 12 हीरोन का सूत्र Ex 12.2

JAC Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8
• Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.9

JAC Class 9 Maths Chapter 14 सांख्यिकी

• Chapter 14 सांख्यिकी Ex 14.1
• Chapter 14 सांख्यिकी Ex 14.2
• Chapter 14 सांख्यिकी Ex 14.3
• Chapter 14 सांख्यिकी Ex 14.4

JAC Class 9 Maths Chapter 15 प्रायिकता

• Chapter 15 प्रायिकता Ex 15.1

Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् शब्दरूप प्रकरणम् Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् शब्दरूप प्रकरणम्

संस्कृत भाषा में प्रयोग करने के लिए इन शब्दों को ‘पद’ बनाया जाता है। संज्ञा, सर्वनाम आदि शब्दों को पद बनाने हेतु इनमें प्रथमा, द्वितीया आदि विभक्तियाँ लगाई जाती हैं। इन शब्दरूपों (पदों) का प्रयोग (पुंल्लिङ्ग, स्त्रीलिङ्ग और नपुंसकलिङ्ग तथा एकवचन, द्विवचन और बहुवचन में भिन्न-भिन्न रूपों में) होता है। इन्हें सामान्यतया शब्दरूप कहा जाता हैं।

संज्ञा आदि शब्दों में जुड़ने वाली विभक्तियाँ सात होती हैं। इन विभक्तियों के तीनों वचनों (एक, द्वि, बहु) में बनने वाले रूपों के लिए जिन विभक्ति-प्रत्ययों की पाणिनि द्वारा कल्पना की गई है, वे ‘सुप्’ कहलाते हैं। इनका परिचय इस प्रकार है –

संज्ञा शब्दरूप-प्रकरणम्

1. अकारान्त पुल्लिंग छात्र’ शब्द

नोट – इसी प्रकार ह्रस्व ‘अ’ पर समाप्त होने वाले पुल्लिंग संज्ञा शब्द- मोहन, शिव, नृप (राजा), राम, सुत (बेटा), गज (हाथी), पुत्र, कृष्ण, जनक (पिता), पाठ, ग्राम, विद्यालय, अश्व (घोड़ा), ईश्वर (ईश या स्वामी), बुद्ध, मेघ (बादल), नर (मनुष्य), युवक (जवान), जन (मनुष्य), पुरुष, वृक्ष, सूर्य, चन्द्र (चन्द्रमा), सज्जन, विप्र (ब्राह्मण), क्षत्रिय, दुर्जन (दुष्ट पुरुष), प्राज्ञ (विद्वान्), लोक (संसार), उपाध्याय (गुरु), वृद्ध (बूढा), शिष्य, प्रश्न, सिंह (शेर), वेद, क्रोश (कोस), भर्प ,सागर (समुद्र), कृषक (किसान), छात्र (बालक), मानव, भ्रमर, सेवक, समीर (हवा), सरोवर और यज्ञ आदि के रूप चलते हैं।

विशेष – जिस शब्द में र्, ऋ अथवा ष् होता है, उसके तृतीया एकवचन के तथा षष्ठी बहुवचन के रूप में ‘न्’ के स्था- ‘ण’ हो जाता है। जैसे-‘राम’ शब्द में ‘र’ है। अतः तृतीया एकवचन में रामेण और षष्ठी बहुवचन में ‘रामाणाम्’ रूप बने हैं, किन्तु ‘बालक’ शब्द में र, ऋ अथवा ष् न होने से ‘बालकेन’ व ‘बालकानाम्’ रूप बनते

2. इकारान्त पुल्लिंग ‘हरि’ शब्द

नोट – इस प्रकार ह्रस्व ‘इ’ पर समाप्त होने वाले सभी पुल्लिंग संज्ञा शब्द-‘कवि’, बह्नि (आग), यति, (संन्यासी), नृपति (राजा), भूपति (राजा), गणपति (गणेश), प्रजापति (ब्रह्मा), रवि (सूर्य), कपि (बन्दर), अग्नि (आग), मुनि, जलधि (समुद्र), ऋषि, गिरि (पहाड़), विधि (ब्रह्मा), मरीचि (किरण), सेनापति, धनपति (सेठ), विद्यापति (विद्वान्), असि (तलवार), शिवि (शिवि नाम का राजा), ययाति (ययाति नाम का राजा) और अरि (शत्रु) आदि के रूप चलते हैं।

विशेष – जिन शब्दों में र, ऋ अथवा ष् होता है, उनमें तृतीया एकवचन में व षष्ठी बहुवचन में ‘न्’ के स्थान पर ‘ण’ हो जाता है। जैसे-हरि शब्द (रि में र होने के कारण)तृतीया एकवचन में हरिणा’ होगा तथा षष्ठी बहुवचन में ‘हरीणाम्’ होगा किन्तु ‘कवि’ में र, ऋ अथवा ए नहीं होने के कारण ‘कविना’ तथा कवीनाम्’ ही हुए हैं।

3. ऋकारान्त पुंल्लिग ‘पितृ’ (पिता) शब्द

नोट – इसी प्रकार ह्रस्व (छेटी) ‘ऋ’ से अन्त होने वाले अन्य पुल्लिग शब्दों-भ्रातृ (भाई) और जामातृ (जमाई, दामाद) आदि के रूप चलेंगे।

4. गो (धेनुः) (ओकारान्तः पुल्लिंगः स्त्रीलिङ्गश्च) शब्दः

5. उकारान्त पुल्लिग’गुरु’ शब्द

नोट – इसी प्रकार भानु, साधु, शिशु, इन्दु, रिपु, शत्रु, शम्भु, विष्णु आदि शब्दों के रूप चलते हैं।

6. ईकारान्त स्त्रीलिंग ‘नदी’ शब्द

नोट – इसी प्रकार दीर्घ (बड़ी) ‘ई’ से अन्त होने वाले स्त्रीलिंग शब्दों-देवी, भगवती, सरस्वती, श्रीमती, कुमारी (अविवाहिता), गौरी (पार्वती), मही (पृथ्वी), पुत्री (बेटी), पत्नी, राज्ञी (रानी), सखी (सहेली), दासी (सेविका), रजनी (रात्रि), महिषी (रानी, भैंस), सती, वाणी, नगरी, पुरी, जानकी और पार्वती आदि शब्दों के रूप चलते हैं।

7. वधू (बहू) शब्द (ऊकारान्त) स्त्रीलिंग

8. मातृ (माता) ऋकारान्त स्त्रीलिंग शब्द

इसी प्रकार ह्रस्व (छोटी) ‘ऋ’ से अन्त होने वाले अन्य सभी स्त्रीलिंग शब्दों-दुहितु (पुत्री) और यातृ (देवरानी) आदि के रूप चलेंगे।

नोट – ‘मातृ’ शब्द के द्वितीया विभक्ति के बहुवचन के ‘मातः’ इस रूप को छोड़कर शेष सभी रूप ‘पितृ’ शब्द के समान ही चलते हैं।

9. उकारान्त स्त्रीलिंग’धेनु’ (गाय) शब्द

नोट – इस प्रकार ह्रस्व ‘उ’ से अन्त होने वाले स्त्रीलिंग शब्दों-तनु (शरीर), रेणु (धूल), रज्जु (रस्सी), कामधेनु, चञ्चु (चोंच) और हनु (ठोड़ी) आदि के रूप चलते हैं।

विशेष-धेनु शब्द के चतुर्थी, पञ्चमी, षष्ठी और सप्तमी विभक्ति के एकवचन के दो-दो रूप बनते हैं। इनमें से प्रथम रूप नदी शब्द के समान बनता है तथा द्वितीय रूप भान शब्द के समान बनता है। इन दो रूपों में से किसी भी एक रूप को प्रयोग में लाया जा सकता है।

सर्वनाम शब्दरूप-प्रकरणम्

10. अस्मद् (मैं) शब्द

नोट – ‘अस्मद्’ शब्द के रूप तीनों लिंगों में समान होते

11. युष्मद् (तुम) शब्द

नोट – ‘युष्मद्’ शब्द के रूप तीनों लिंगों में समान होते

12. सर्व (सब) पुल्लिंग शब्द

13. सर्व (सब) स्त्रीलिंग शब्द

14. सर्व (सब) नपुंसकलिंग शब्द

नोट – शेष विभक्तियों के रूप पुल्लिंग ‘सर्व’ की तरह चलेंगे।

15. तत्/तद् (वह) पुल्लिंग शब्द

नोट – प्रथमा विभक्ति एकवचन को छोड़कर सभी रूपों का आधार ‘त’ अक्षर है तथा ‘सर्व’ शब्द के समान रूप हैं।

16. तत् / तद् (वह) स्त्रीलिंग शब्द

17. तत् / तद (वह) नपुंसकलिंग

नोट – ‘तद्’ नपुंसकलिंग के तृतीया विभक्ति से सप्तमी विभक्ति तक के ये सभी रूप तद्’ पुल्लिंग के समान चलते

18. यत् (जो) पुंल्लिग शब्द

नोट – इस ‘यत्’ शब्द का सभी लिंगों में, सभी विभक्तियों के रूप में ‘य’ आधार रहेगा तथा इसके ‘सर्व’ के समान ही रूप चलेंगे।

19. यत् (जो) स्त्रीलिंग शब्द

20. यत् (जो) नपुंसकलिंग शब्द

नोट – ‘यत्’ नपुंसकलिंग के तृतीया विभक्ति से सप्तमी विभक्ति तक के सम्पूर्ण रूप ‘यत्’ पुंल्लिंग के समान ही चलेंगे।

21. किम् (कौन) पुंल्लिंग शब्द

नोट – ‘किम्’ शब्द के रूपों का मूल आधार सभी लिंगों एवं विभक्तियों में ‘क’ होता है तथा इसके रूप ‘सर्व’ शब्द के समान ही चलते हैं।

22. किम् (कौन) स्त्रीलिंग शब्द

23. किम् (कौन) नपुंसकलिंग शब्द

नोट – ‘किम्’ शब्द के नपुंसकलिंग के तृतीया विभक्ति से सप्तमी विभक्ति तक के सभी रूप ‘किम्’ पुल्लिंग के समान ही चलते हैं।

अभ्यासः

प्रश्न 1.
अधोलिखित प्रश्नेषु सम्यक् विकल्प चिनुत –
1. ‘बालक’ तृतीया विभक्ति एकवचन –
(अ) बालक
(ब) बालकेन
(स) बालकस्य
(द) बालकः
उत्तरम् :
(ब) बालकेन

2. ‘पति’ (स्वामी) षष्ठी द्विवचन –
(अ) पती
(ब) पत्युः
(स) पत्यौ
(द) पतिभ्यः
उत्तरम् :
(स) पत्यौ

3. ‘गुरु’ चतुर्थी विभक्ति बहुवचन –
(अ) गुरूणा
(ब) गुरौ
(स) गुरुभिः
(द) गुरुभ्यः
उत्तरम् :
(द) गुरुभ्यः

4. ‘सखि’ द्वितीया विभक्ति एकवचन –
(अ) सख्यौ
(ब) सखीनाम्
(स) सखायम्
(द) सख्युः
उत्तरम् :
(स) सखायम्

5. ‘स्त्री’ प्रथमा विभक्ति बहुवचन –
(अ) स्त्रियः
(ब) स्त्रीभ्यः
(स) स्त्रीभ्याम्
(द) स्त्रयाः
उत्तरम् :
(अ) स्त्रियः

6. ‘विभा’ सप्तमी विभक्ति एकवचन –
(अ) विभासु
(ब) विभाभ्यः
(स) विभायाम्
(द) हे विभाः
उत्तरम् :
(स) विभायाम्

7. ‘पुस्तक’ पञ्चमी विभक्ति द्विवचन –
(अ) पुस्तकम्
(ब) पुस्तकाभ्याम्
(स) पुस्तकाय
(द) पुस्तकयोः
उत्तरम् :
(ब) पुस्तकाभ्याम्

8. ‘आत्मन्’ सप्तमी द्विवचन –
(अ) आत्मनः
(ब) आत्मभ्याम्
(स) आत्मानौ
(द) आत्मनोः
उत्तरम् :
(द) आत्मनोः

9. ‘पितृ’ प्रथमा बहुवचन –
(अ) पितरि
(ब) पित्रोः
(स) पितरः
(द) पित्रा
उत्तरम् :
(स) पितरः

10. ‘भगवत्’ तृतीया विभक्ति बहुवचन –
(अ) भगवद्भिः
(ब) भगवत्सु
(स) भगवन्तः
(द) भगवते
उत्तरम् :
(अ) भगवद्भिः

11. ‘सर्व’ पुल्लिंग सप्तमी विभक्ति एकवचन –
(अ) सर्वेषु
(ब) सर्वयोः
(स) सर्वस्मिन्
(द) सर्वैः
उत्तरम् :
(स) सर्वस्मिन्

12. अस्मद् (मैं) तृतीया विभक्ति बहुवचन –
(अ) मह्यम्
(ब) अस्माकम्
(स) आवयोः
(द) अस्माभिः
उत्तरम् :
(द) अस्माभिः

13. किम् (कौन) स्त्रीलिंग,पंचमी विभक्ति, द्विवचन –
(अ) कयोः
(ब) काभ्याम्
(स) कासाम्
(द) के
उत्तरम् :
(ब) काभ्याम्

14. अस्मिन् वाक्ये सर्वनाम पदं किम्? ‘सा विद्यालये संस्कृत पठति।’
(अ) विद्यालये
(ब) पठति
(स) सा
(द) संस्कृतं
उत्तरम् :
(स) सा

15. इदम् मनीषस्य पुस्तकं अस्ति। अस्मिन् वाक्ये सर्वनाम पदं किम्?
(अ) पुस्तकं
(ब) अस्ति
(स) इदम्
(द) मनीषस्य
उत्तरम् :
(स) इदम्

16. भवत्याः गृहं अति शोभनं अस्ति। अस्मिन् वाक्ये सर्वनाम पदं किम् –
(अ) गृहं
(ब) अति
(स) शोभनं
(द) भवत्याः
उत्तरम् :
(द) भवत्याः

17. …………… प्रभावेन सिंहः सजीवः अभवत? रिक्त स्थाने उचितं सर्वनाम पदं किम् –
(अ) केन
(ब) कस्मात्
(स) के
(द) कस्य
उत्तरम् :
(अ) केन

18. अस्मिन् वाक्ये सर्वनाम पदः नास्ति-अहं तव तस्य च मित्र।
(अ) तव
(ब) तस्य
(स) अहं
(द) मित्रं
उत्तरम् :
(ब) तस्य

19. अस्मिन् वाक्ये सर्वनाम पदः अस्ति-तस्य भ्राता ग्रामं गच्छति।
(अ) तस्य
(ब) ग्रामं
(स) भ्राता
(द) गच्छति
उत्तरम् :
(अ) तस्य

20. युष्मद् (तुम) शब्दस्य पंचमी बहुवचने रूपं भवति –
(अ) युष्माकम्
(ब) युष्मत्
(स) युष्मानम्
(द) युष्मासु
उत्तरम् :
(स) युष्मानम्

प्रश्न 2.
कोष्ठके प्रदत्तं निर्देशानुसारम् उचित विभक्तिपदेन रिक्तस्थानानि पूर्ति कुरुत –
(कोष्ठक में दिये निर्देशानुसार उचित विभक्ति पद से रिक्त स्थानों की पूर्ति कीजिए-)
(i) ……………. पत्रं पतति।’ (वृक्ष-पञ्चमी)
(ii) ……………… हरीशः विनम्रः।(छात्र-सप्तमी)
(iii) भो ………………. पत्रं पठ। (महेश-सम्बोधन)
(iv) ………………. किं हसन्ति ? (भवान्-प्रथम)
(v) ………………. शनैः शनैः लिखति (केशव-प्रथमा)
(vi) गोपालः जलेन…………………. प्रक्षालयति। (मुख-द्वितीया)
(vii) सेवकः स्कन्धेन………………. वहति। (भार-द्वितीया)
(viii) सः ………………. कोमलः। (स्वभाव-तृतीया)
(ix) कोऽर्थः ………………. यो न विद्वान् न धार्मिकः। (पुत्र-तृतीया)
(x) भक्तः ………………. हरि भजति। (मुक्ति-चतुर्थी)
(xi) क्रीडनकं रोचते। …………….(शिशु-चतुर्थी)
(xii) ज्ञानं गुरुतरम्। (धन-पंचमी)
(xiii) ……………… गङ्गा प्रभवति। (हिमालय-पंचमी)
(xiv) …………….. हेतोः वाराणस्यां तिष्ठति। (अध्ययन-षष्ठी)
(xv) ………………. ओदनं पचति।। (स्थाली-सप्तमी)
उत्तरम्:
(i) वृक्षात्
(ii) छात्रेषु
(iii) महेश !
(iv) भवन्तः
(v) केशवः
(vi) मुखं
(vii) भारं
(viii) स्वभावेन
(ix) पुत्रेण
(x) मुक्तये
(xi) शिशवे
(xii) धनात्
(xili) हिमालयात्
(xiv) अध्ययनस्य
(xv) स्थाल्याम्।

प्रश्न 3.
कोष्ठकात् उचितविभक्तियुक्तं पदं चित्वा वाक्यपूर्तिः क्रियताम् –
(कोष्ठक से उचित विभक्तियुक्त पद को चुनकर वाक्य-पूर्ति कीजिए-)
(i) ………………. पुरोहितः अकथयत्। (शुद्धोदनाय, शुद्धोदनस्य, शुद्धोदने)
(ii) मम ………………. स्वां दुहितरं यच्छ। (पिता, पित्रा, पित्रे)
(iii) शान्तनुः ……………….. वरम् अयच्छत्। (भीष्माय, भीष्मे, भीष्मात्)
(iv) अयि ………………. मम मित्रं भविष्यति।(चटकपोत!, चटकपोतं, चटकपोतैः)
(v) अस्मिन् ………………. प्रत्येकं स्व-स्वकृत्ये निमग्नो भवति। (जगत. जगता, जगति)
(vi) कस्मिंश्चिद् ………………. एका निर्धना वृद्धा स्त्री न्यवसत्। (ग्रामेन, ग्रामे, ग्रामस्य)
(vii) सा ………………. बहिः आगन्तव्यम्। (ग्रामात्, ग्रामे, ग्रामान्)
(vii) लुब्धया ………………. लोभस्य फलं प्राप्तम्। (बालिका, बालिकया, बालिकाया:)
(ix) इन्दुः ……………… प्रकाशं लभते। (भानुना, भानोः, भानवे)
(x) ……………. गङ्गा सर्वश्रेष्ठा। (नद्याम्, नद्याः नदीषु)
(xi) भो भगवन् ! ………………… दयस्व।(मयि, माम्, अहं)
(xii) ………………. सर्वत्र पूज्यते। (विद्वान्, विद्वांसः विद्वांसी)
(xiii) रविः प्रतिदिनं ………………. नमति। (ईश्वराय, ईश्वरे, ईश्वरम्)
(xiv) सः ……………… पश्यति। (राजानम्, राज्ञाम्, राज्ञा)
(xv) रामः ………………. पटुतरः। (मोहनेन, मोहनस्य, मोहनात्)
उत्तरम्-
(i) शुद्धोदनस्य
(ii) पित्रे
(iii) भीष्माय
(iv) चटकपोत!
(v) जगति
(vi) ग्रामे
(vil) ग्रामात्
(viii) बालिकया
(ix) भानुना
(x) नदीषु
(xi) मयि
(xii) विद्वान्
(xiii) ईश्वरम्
(xiv) राजानम्
(xv) मोहनात्।

प्रश्न 4.
समुचितं विभक्तिप्रयोगं कृत्वा रिक्तस्थानानि पूरयत –
(उचित विभक्ति का प्रयोग करके रिक्त-स्थानों की पूर्ति कीजिए-)
1. …………….. कुत्र गच्छति? (भवत्)
2. ……………. मोदकं रोचते। (बालक)
3. …………… अभितः वनं अस्ति। (ग्राम)
4. कर्णः ………………. सह नगरं गच्छति। (पिता)
5. गङ्गा ……………. उद्भवति। (हिमालय)
6. ………………. कक्षायां बालकाः पठन्ति। (इदम्)
7. सः………………. अधितिष्ठति। (आसन)
8. मुनिः ………………. लोकं जयति। (सत्य)
9. नृपः ………………. क्रुध्यति। (दुर्जन)
10. बालकः…………….. बिभेति। (चोर)
उत्तरम् :
(1) भवान्
(ii) बालकाय
(iii) ग्रामम्
(iv) पित्रा
(v) हिमालयात्
(vi) अस्याम्
(vii) आसनम्
(viii) सत्येन
(ix) दुर्जनेभ्यः
(x) चोरात्।

प्रश्न 5.
कोष्ठके प्रदत्तं निर्देशानुसारम् उचितविभक्तिपदेन रिक्तस्थानानां पूर्ति कुरुत –
(कोष्ठक में दिये निर्देशानुसार उचित विभक्ति पद से रिक्त स्थानों की पूर्ति कीजिए-)
(i) …………… च एका दुहिता आसीत्। (तत्-स्त्रीलिंग षष्ठी)
(ii) …………….. विस्मयं गता। (तत्-स्त्रीलिंग प्रथमा)
(iii) ………………….. मम श्वश्रूः सदैव मर्मघातिभिः कटुवचनैराक्षिपति माम्। (इदम्-स्त्रीलिंग प्रथम)
(iv) …………………… काकिणी अपि न दत्ता। (यत्-पुल्लिग तृतीया)
(v) …………… तदेव वक्तव्यं वचने का दरिद्रता। (तत्-पुल्लिंग पंचमी)
(vi) ………………. मरालैः सह विप्रयोगः। (यत्-पुंल्लिग षष्ठी)
(vii) ………………. अनुकूले स्थिते शक्रोऽपि नास्मान् बाधितुं शक्नुयात्। (इदम्-ऍल्लिंग सप्तमी)
(viii) तत् ……………. अस्मात् मनोरथमभीष्टं साधयामि। (अस्मद्-प्रथमा)
(ix) किन्तु …………………. सह केलिभिः कोऽपि न उपलभ्यमानः आसीत्।। (तत्-पुंल्लिंग तृतीया)
(x) अयि चटकपोत ! ……….. मित्रं भविष्यसि। (अस्मद्-षष्ठी)
(xi) अपूर्वः इव ते हर्षो ब्रूहि ……….. असि विस्मितः। (किम्-पुंल्लिंग तृतीया)
(xii) …………………. कुले आत्मस्तवं कर्तुमनुचितम्। (अस्मद्-षष्ठी)
(xiii) तां च …………… चित् श्रेष्ठिनो गृहे निक्षेपभूतां कृत्वा देशान्तरं प्रस्थितः। (किम्-पुल्लिंग षष्ठी)
(xiv) वत्स! पितृव्योऽयं ………….. (युष्मद्-षष्ठी)
(xv) ……………….. अस्मि तपोदत्तः। (अस्मद्-प्रथमा)
(xvi) गुरुगृहं गत्वैव विद्याभ्यासो ……………. करणीयः। (अस्मद्-तृतीया)
(xvii) …………………. शब्दमवसुप्तस्तु जटायुरथ शुश्रुवे। (तत्-पुल्लिंग द्वितीया)
(xviii) वृद्धोऽहं ………………. युवा धन्वी सरथः कवची शरी। (युष्मद्-प्रथमा)
(xix) यतः ……………….. स्थलमलापनोदिनी जलमलापहारिणश्च। (तत्-पुल्लिंग प्रथमा)
(xx) ………………. सर्वान् पुष्णाति विविधैः प्रकारैः। (इदम्-स्त्रीलिंग प्रथमा)
उत्तरम् :
(i) तस्याः
(ii) सा
(iii) इयम्
(iv) येन
(v) तस्मात्
(vi) येषाम्
(vii) अस्मिन्
(viii) अहम्
(ix) तेन
(x) मम
(i) केन
(xii) अस्माकं
(xiii) कस्य
(xiv) तव
(xv) अहम्
(xvi) मया
(xvii) तम्
(xviii) त्वम्
(xix) स:
(xx) इयम्।

प्रश्न 6.
कोष्ठकात् उचितविभक्तियुक्तं पदं चित्वा वाक्यपूर्तिः क्रियताम् –
(कोष्ठक से उचित विभक्ति युक्त पद को चुनकर वाक्य की पूर्ति कीजिए-)
(i) नाऽहं जाने ……………… कोऽस्ति भवान्। (यत्, याभ्याम्, याः)
(ii) सिकता: जलप्रवाहे स्थास्यन्ति ……………….? (किम्, कानि, काषु)
(ii) त्वया ………………. पूर्वेषाम् अभीष्टाः कामाः पूरिताः। (आवाभ्याम्, अस्मत्, अहम्)
(iv) प्रकृतिरेव ………………. विनाशकी सजाता। (तस्य, तयोः, तेषां)
(v) ………………. सर्वमिदानी चिन्तनीयं प्रतिभाति। (तत्, ते, तानि)
(vi) भगवन्। प्रष्टुमिच्छामि किम् …………………. मनः ? (इयं, अयं, इदम्)
(vii) अशितस्यान्नस्य योऽणिष्ठः ………………. मनः। (तत्, तम्, तासाम्)
(viii) बालिका ………………. निवारयन्ती। (तस्मै, ताभ्याम्, तम्)
(ix) परं ………………. माता एकाकिनी वर्तते। (तव, तयोः, तेषु)
(x) ………………. अपि चायपेयस्य नास्ति। (इदम्, इदानीम्, अयम्)
(xi) यत् …………….. अपि कथनीयं यां प्रत्येव कथय। (किम्, कौ, कानि)
(xii) ……………….. नृशंसाः। (मह्यम्, अस्मत्, वयम्)
(xiii) ………………. इदानी कुत्र गताः ? (ते, ताभ्याम्, तेभ्यः)
(xiv) कल्पतरु: ……………….. उद्याने तिष्ठति स तव सदा पूज्य:। (तव, तेभ्यः, तस्मै)
(xv) विषाक्तं जलं नद्यां निपात्यते ………………. मत्स्यादीनां जलचराणां च नाशो जायते। (येन, याभ्यां, याषु)
उत्तरम् :
(i) यत्
(ii) किम्
(iii) अस्मत्
(iv) तेषां
(v) तत्
(vi) इदम्
(vii) तत्
(viii) तम्
(ix) तव
(x) इदानीम्
(xi) किम्
(xii) वयम्
(xiii) ते
(xiv) तव
(xv) येन।

प्रश्न 7.
अधोलिखितानां शब्दरूपाणां वाक्येषु प्रयोगं कुरुत-
(निम्नलिखित शब्दरूपों का वाक्यों में प्रयोग करो-)
पूर्वस्या, द्वितीयम्, सखा, रमायै, पूर्वे, हरिः, पितृभ्यः, सखिषु, स्वसुः, राज्ञाम्, भवान्, भवती, विद्वांसः, अमूः, दिक्षु, सरितः, कर्मणा, नव, वाक्, पञ्च।
उत्तराणि :
1. सूर्यः पूर्वस्याम् दिशि उदेति।
2. कक्षायां मम द्वितीय स्थानमस्ति।
3. रमेशः मम सखा अस्ति।
4. फलानि रमायै सन्ति।
5. मोहनः पूर्वे कर्णपुरनगरे निवसति स्म।
6. हरिः विद्यालयं गच्छति।
7. राकेशः पितृभ्यः जलं समर्पयति।
8. सखिषु रमा सुन्दरतमा अस्ति।
9. रामः श्वः स्वसुः गृहं गमिष्यति।
10. राज्ञाम् आचारः शोभनः भवति।
11. भवान् कुत्र निवसति ?
12. भवती किं पठति ?
13. स्वदेशे पूज्यते राजा, विद्वांसः सर्वत्र पूज्यन्ते।
14. अमूः कुत्र वसन्ति ?
15. दिक्षु कृष्णाः वारिदाः सन्ति।
16. सरितः जलं शीतलं भवति।
17. कर्मणा विना जीवनं न अस्ति।
18. तत्र विद्यालये नव छात्राः सन्ति।
19. जनस्य वाक् मधुरं भवेत।
20. पञ्च पाण्डवाः विज्ञाः आसन्।

प्रश्न 8.
निर्देशानुसार सर्वनाम शब्दानां रूपं लिखत –
(निर्देशानुसार सर्वनाम शब्दों के रूप लिखिए-)
1. (i) सर्व – (पुल्लिंग प्रथमा विभक्ति बहुवचन)
(ii) तत् – (नपुंसकलिंग सप्तमी विभक्ति एकवचन)
2. (i) भवती – (तृतीया विभक्ति एकवचन)
(ii) यत् – (पुल्लिंग षष्ठी विभक्ति बहुवचन)
3. (i) इदम् – (स्त्रीलिंग द्वितीया विभक्ति बहुवचन)
(ii) एतत् – (पुल्लिंग पंचमी विभक्ति एकवचन)
4. (i) भवत् – (तृतीया विभक्ति द्विवचन)
(ii) किम् – (पुल्लिंग षष्ठी विभक्ति एकवचन)
5. (i) सर्व – (स्त्रीलिंग चतुर्थी विभक्ति एकवचन)
(ii) किम् – (नपुंसकलिंग सप्तमी विभक्ति बहुवचन)
6. (i) युष्मद् – (द्वितीया विभक्ति बहुवचन)
(ii) एतत् – (नपुंसकलिंग सप्तमी विभक्ति द्विवचन)
7. (i) सर्व – (नपुंसकलिंग चतुर्थी विभक्ति द्विवचन)
(ii) किम् – (स्त्रीलिंग पंचमी विभक्ति बहुवचन)
8. (i) इदम् – (पुल्लिग प्रथमा विभक्ति बहुवचन)
(ii) यत् – (स्त्रीलिंग पंचमी विभक्ति बहुवचन)
9. (i) इदम् – (नपुंसकलिंग तृतीया विभक्ति बहुवचन)
(ii) तत् – (पुल्लिंग षष्ठी विभक्ति एकवचन)
10. (i) अस्मद् – (चतुर्थी विभक्ति एकवचन)
(ii) एतत् – (स्त्रीलिंग सप्तमी विभक्ति बहुवचन)
11. (i) सर्व – (पुल्लिंग प्रथमा विभक्ति एकवचन)
(ii) तत् – (नपुंसकलिंग सप्तमी विभक्ति बहुवचन)
12. (i) भवती – (प्रथमा विभक्ति द्विवचन)
(ii) यत् – (पुल्लिग सप्तमी विभक्ति एकवचन)
13. (i) इदम् – (स्त्रीलिंग प्रथमा विभक्ति बहुवचन)
(i) एतत् – (पुल्लिंग सप्तमी विभक्ति द्विवचन)
14. (i) भवत् – (द्वितीया विभक्ति एकवचन)
(ii) किम् – (पुल्लिंग षष्ठी विभक्ति बहुवचन)
15. (i) सर्व – (स्त्रीलिंग द्वितीया विभक्ति द्विवचन)
(ii) किम् – (नपुंसकलिंग षष्ठी विभक्ति एकवचन)
16. (i) युष्मद् – (द्वितीया विभक्ति द्विवचन)
(ii) एतत् – (नपुंसकलिंग षष्ठी विभक्ति द्विवचन)
17. (i) सर्व – (नपुंसकलिंग तृतीया विभक्ति एकवचन)
(ii) किम् – (स्त्रीलिंग पंचमी विभक्ति एकवचन)
18. (i) इदम् – (पुल्लिंग तृतीया विभक्ति द्विवचन)
(ii) यत् – (स्त्रीलिंग पंचमी विभक्ति एकवचन)
19. (i) इदम् – (नपुंसकलिंग तृतीया विभक्ति बहुवचन)
(ii) तत् – (पुल्लिंग पंचमी विभक्ति द्विवचन)
20. (i) अस्मद् – (चतुर्थी विभक्ति बहुवचन)
(ii) एतत् – (स्त्रीलिंग सप्तमी विभक्ति एकवचन)
उत्तराणि :
1. (i) सर्वे (ii) तस्मिन्
2. (i) भवत्या (i) येषाम्
3. (i) इमाः (ii) एतस्मात्
4. (i) भवद्भ्याम् (ii) कस्य
5. (i) सर्वस्यैः (ii) केषु
6. (i) युष्मान् (ii) एतयोः
7. (i) सर्वाभ्याम् (ii) काभ्यः
8. (i) इमे (ii) याभ्यः
9. (i) एभिः (ii) तस्य
10. (i) मह्यम् (ii) एतासु
11. (i) सर्वः (ii) तेषु
12. (i) भवत्यौ (ii) यस्मिन्
13. (i) इमाः (ii) एतयोः
14. (i) भवन्तम् (ii) केषाम्
15. (i) सर्वे (ii) कस्य
16. (i) युवाम् (ii) एतयोः
17. (i) सर्वेण (ii) कस्याः
18. (i) आभ्याम् (ii) यस्याः
19. (i) एभिः (ii) ताभ्याम्
20.(i) अस्मभ्यम् (ii) एतस्याम्।

प्रश्न 9.
निर्देशानुसारं शब्द-रूपं लिखत – (निर्देशानुसार शब्द-रूप लिखिए-)
1. (i) धेनु – (तृतीया विभक्ति बहुवचन)
(ii) प्रासाद – (सप्तमी विभक्ति एकवचन)
2. (i) स्वसृ – (चतुर्थी विभक्ति एकवचन)
(ii) विधातृ – (पुल्लिंग सप्तमी विभक्ति बहुवचन)
3. (i) पितृ – (षष्ठी विभक्ति बहुवचन)
(ii) तनु – (प्रथमा विभक्ति बहुवचन)
4. (i) फलम् – (सप्तमी विभक्ति बहुवचन)
(ii) रमा – (तृतीया विभक्ति एकवचन)
5. (i) जगत् – (षष्ठी विभक्ति बहुवचन)
(ii) धेनु – (प्रथमा विभक्ति बहुवचन)
6. (i) नदी – (प्रथमा विभक्ति बहुवचन)
(ii) मातृ – (तृतीया विभक्ति एकवचन)
7. (i) भ्रातृ – (पंचमी विभक्ति द्विवचन)
(ii) आशु – (सप्तमी विभक्ति एकवचन)
8. (i) प्रासाद – (द्वितीया विभक्ति एकवचन)
(ii) पितृ – (तृतीया विभक्ति बहुवचन)
9. (i) वेदना – (पंचमी विभक्ति एकवचन)
(ii) धातृ – (द्वितीया विभक्ति द्विवचन)
10. (i) शान्तनु – (षष्ठी विभक्ति एकवचन)
(ii) दातृ – (चतुर्थी विभक्ति एकवचन)
11. (i) गंगा – (पंचमी विभक्ति बहुवचन)
(ii) कर्तृ – (तृतीया विभक्ति बहुवचन)
12. (i) धीवर – (षष्ठी विभक्ति द्विवचन)
(ii) हर्तृ – (सप्तमी विभक्ति बहुवचन)
13. (i) कन्या – (सप्तमी विभक्ति द्विवचन)
(ii) भ्रातृ – (द्वितीया विभक्ति एकवचन)
14. (i) गृहम् – (द्वितीया विभक्ति बहुवचन)।
(ii) दुहितृ – (सप्तमी विभक्ति एकवचन)
15. (i) सेवा – (प्रथमा विभक्ति बहुवचन)
(ii) स्वसू – (षष्ठी विभक्ति एकवचन)
16. (i) भानु – (चतुर्थी विभक्ति एकवचन)
(ii) ननान्दृ – (पंचमी विभक्ति बहुवचन)
17. (i) रज्जु – (द्वितीया विभक्ति द्विवचन)
(ii) भ्रातृ – (सप्तमी विभक्ति एकवचन)
18. (i) पशु – (प्रथमा विभक्ति बहुवचन)
(ii) विधातृ – (षष्ठी विभक्ति बहुवचन)
19. (i) धेनु – (द्वितीया विभक्ति एकवचन)
(ii) भगवत् – (पंचमी विभक्ति एकवचन)
20. (i) तनु – (तृतीया विभक्ति एकवचन)
(ii) जगत् – (सप्तमी विभक्ति बहुवचन)
उत्तराणि :
1. (i) धेनुभिः (ii) प्रासादे
2. (i) स्वस्रे (ii) विधातृषु
3. (i) पितृणाम् (i) तनवः
4. (i) फलेषु (ii) रमया
5. (i) जगताम् (ii) धेनवः
6. (i) नद्यः (ii) मात्रा
7. (i) भ्रातुः (ii) आशौ
8. (i) प्रासादम् (ii) पितृभिः
9. (i) वेदनायाः (ii) धातरौ
10. (i) शान्तनो: (ii) दात्रे
11. (i) गंगाभ्यः (ii) कर्तृभि
12. (i) धीवरयोः (ii) हर्तृषु,
13. (i) कन्ययोः (ii) भ्रातरम्
14. (i) गृहाणि (ii) दुहितरि
15. (i) सेवाः (ii) स्वसुः
16. (i) भानवे (ii) ननान्दृभ्यः
17. (i) रज्जू (ii) भ्रातरि
18. (i) पशव: (ii) विधातृणाम्
19. (i) धेनुम् (ii) भगवतः
20. (i) तन्वा (ii) जगत्सु।

प्रश्न 10.
अधोलिखितेषु शब्देषु विभक्तिः वचनं च निर्देशनं कुरुत-
(निम्नलिखित शब्दों में विभक्ति और वचन को निर्देशित कीजिए-)
(i) गुरुणा
(ii) विद्यालयेषु
(iii) देवानाम्
(iv) लतायाम्
(v) मुनीन्
(vi) वारिणि
(vii) त्वाम्
(viii) कैः
(ix) यस्मै
(x) एतस्मात्।
उत्तरम् :
(i) तृतीया विभक्तिः एकवचनम्
(ii) सप्तमी विभक्तिः बहुवचनम्
(iv) षष्ठी विभक्तिः बहुवचनम्
(iv) सप्तमी विभक्तिः एकवचनम्
(v) द्वितीया विभक्तिः बहुवचनम्
(vi) द्वितीया विभक्तिः बहुवचनम्
(vii) द्वितीया विभक्तिः एकवचनम्
(viii) तृतीया विभक्ति: बहुवचनम्
(ix) चतुर्थी विभक्तिः एकवचनम्
(x) पञ्चमी विभक्तिः एकवचनम्।

Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् उपसर्ग प्रकरणम् Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् उपसर्ग प्रकरणम्

उपसर्ग की परिभाषा – शब्द या धातु (क्रिया) के पूर्व जो पद जोड़े या लगाये जाते हैं वे उपसर्ग कहे जाते हैं। उपसर्ग का प्रयोग करने से धातु के अर्थ में विशेषता आ जाती है। कहीं धातु का अर्थ परिवर्तित होकर एक नया अर्थ प्रकट करता है तो कहीं अर्थ का विपर्ययं या विलोम हो जाता है और इस प्रकार अर्थ में सौन्दर्य आ जाता है। जैसे –

उपर्युक्त सभी उपसर्गयुक्त शब्द एक ही धातु (क्रिया) शब्द के साथ भिन्न-भिन्न उपसर्ग जोड़ने से बने हैं, किन्तु उनके अर्थ बिल्कुल बदल गये हैं।
कुल उपसर्ग 22 होते हैं जो इस प्रकार हैं – प्र, परा, अप, सम्, अनु, अव, निस्, निर, दुस्, दुर्, वि, आड्. (आ), नि, अधि, अपि, अति, सु, उत्, अभि, प्रति, परि, उप।
अब यहाँ पर कतिपय उपसर्गों व उनसे बने शब्दों को दिया गया है।

1. ‘अव’ उपसर्ग: –

1. अव + जानाति = अवजानाति
2. अव. + क्षिपति = अवक्षिपति
3. अव + तरति = अवतरति
4. अव + नति = अवनति
5. अव + गमनम् = अवगमनम्
6. अव + ज्ञा. = अवज्ञा
7. अव + दानम् = अवदानम्
8. अव + तिष्ठति = अवतिष्ठति
9. अव + गुणः = अवगुणः
10. अव + शेषः = अवशेषः
11. अव + क्षेपणम् = अवक्षेपणम्
12. अव + सरः = अवसरः
13. अव + काशः = अवकाशः
14. अव + गच्छति = अवगच्छति
15. अव + लेहः = अवलेहः
16. अव + गणना = अवगणना
17. अव + धारणा = अवधारणा
18. अव + ग्रहः = अवग्रहः
19. अव + रोहः = अवरोहः
20. अव + रोधः = अवरोधः

2. ‘अप’ उपसर्ग:

1. अप + करोति = अपकरोति
2. अप + सरति = अपसरति
3. अप + ऐति – अपैति
4. अप + ए = अपहरति
5. अप + वादः = अपवादः
6. अप + शब्दः = अपशब्दः
7. अप + कारः = अपकारः
8. अप + आदानम् = अपादानम्
9. अप + कर्षः = अपकर्ष
10. अप + कर्ता = अपकर्ता
11. अप + मानम् = अपमानम्
12. अप + यशः = अपयशः
13. अप + राधः = अपराधः
14. अप + ज्ञानम् = अपज्ञानम्
15. अप + हरणम् = अपहरणम्
16. अप + भ्रंशः = अपभ्रंशः
17. अप + व्ययः = अपव्ययः
18. अप + हरति = अपहरति
19. अप + कारीः = अपकारीः
20. अप + चारी = अपचारी

3. ‘निस्’ उपसर्गः –

1. निस् + तेज = निस्तेज
2. निस् + काम = निष्काम
3. निस् + तार = निस्तार
4. निस् + चय = निश्चय
5. निस् + सार = निस्सार
6. निस् + सरति = निस्सरति
7. निस् + प्राणः = निष्प्राणः
8. निस् + क्रियः = निष्क्रियः
9. निस + चलः = निश्चलः
10. निस् + फलम् = निष्फलम्
11. निस् + कपटः = निष्कपटः
12. निस् + तारणम् = निस्तारणम्
13. निस् + प्रयोजनम् = निष्प्रयोजनम्
14. निस् + छलः = निश्छलः
15. निस् + कृतिः = निष्कृतिः
16. निस् + पापम् = निष्पापम्
17. निस् + चितः = निश्चितः
18. निस् + कर्षः = निष्कर्षः

4. ‘निर्’ उपसर्गः

1. निर् + ईक्षते = निरीक्षते
2. निर् + वहति = निर्वहति
3. निर् + अस्यति = निरस्यति
4. निर् + गच्छति = निर्गच्छति
5. निर् + भय = निर्भय
6. निर् + वचनम् = निर्वचनम्
7. निर् + आकरणम्= निराकरणम्
8. निर् + धनः = निर्धनः
9. निर् + नयः = निर्णयः
10. निर् + गमनम् = निर्गमनम्
11. निर् + वाहः, = निर्वाहः
12. निर् + जनम् = निर्जनम्
13. निर् + वेदः = निर्वेदः
14. निर् + अस्तम् = निरस्तम्
15. निर् + नायकः = निर्णायकः
16. निर् + ईक्षणम् = निरीक्षणम्
17. निर् + देशः = निर्देशः
18. निर् + आदरः = निरादरः
19. निर् + मूलम् = निर्मूलम्

5. ‘दुर्’ उपसर्ग:

1. दुर् + बोधति = दुर्बोधति
2. दुर् + गच्छति = दुर्गच्छति
3. दुर् + नयति = दुर्नयति
4. दुर् + वचनम् = दुर्वचनम्
5. दुर् + दैवम् = दुर्दैवम्
6. दुर् + दशा = दुर्दशा
7. दुर् + आशा = दुराशा
8. दुर् + जनः = दुर्जनः
9. दुर् + बोधः = दुर्बोध:
10. दुर् + गन्धः = दुर्गन्धः
11. दुर् + गमः = दुर्गमः
12. दुर् + लभः = दुर्लभः
13. दुर् + आचरणम्= दुराचरणम्
14. दुर् + गः = दुर्गः
15. दुर् + व्यवहारः = दुर्व्यवहारः
16. दुर् + दिनम् = दुर्दिनम्
17. दुर् + आचारः = दुराचारः
18. दुर् + अवस्था = दुरवस्था
19. दुर् + योधनः = दुर्योधनः
20. दुर् + गतिः = दुर्गतिः

6. ‘आङ्’ (आ) उपसर्गः

1. आ + नयति = आनयति
2. आ + चरति = आचरति
3. आ + गच्छति = आगच्छति
4. आ + रोहति = आरोहति
5. आ + गमः = आगमः
6. आ + दरः = आदरः
7. आ + धारः = आधारः
8. आ + गमनम् = आगमनम्
9. आ + गच्छति = आगच्छति
10. आ + नी = आनयति
11. आ + चरणम् = आचरणम्
12. आ + दाय = आदाय
13. आ + हरति = आहरति
14. आ. + मरणम् = आमरणम्
15. आ + दानम् = आदानाम्
16. आ + चारः = आचारः
17. आ + कर्षणम् = आकर्षणम्
18. आ + गमनम् = आगमनम्
19. आ + ग्रहः = आग्रहः
20. आ + ज्ञा आज्ञा

7. ‘उत्’ उपसर्ग:

1. उत् + गच्छति = उद्गच्छति
2. उत् + भवति = उद्भवति
3. उत् + तिष्ठति = उत्तिष्ठति
4. उत् + हरति = उद्धरति
5. + सवः = उत्सवः
6. उत् + पत्ति – उत्पत्तिः
7. उत् + पतति = उत्पतति
8. उत् + क्षेपणम् = उत्क्षेपणम्
9. उत् + तेजकः = उत्तेजकः
10. उत् + साहः = उत्साहः
11. उत् + सर्गः = उत्सर्गः
12. उत् + थानम् = उत्थानम्
13. उत् + जवलः = उज्ज्वलः
14. उत् + गमनम् = उदगमनम्
15. उत् + भवः = उद्भवः
16. उत् + तरम् = उत्तरम्
17. उत् + तमः = उत्तमः
18. उत् + कण्ठा = उत्कण्ठा
19. उत् + कर्षः = उत्कर्षः
20. उत् + हारः = उद्धारः

8. ‘अधि’ उपसर्गः

1. अधि + करोति = अधिकरोति
2. अधि + गच्छति = अधिगच्छति
3. अधि + अस्ति = अध्यास्ते
4. अधि + वसति = अधिवसति
5. अधि + कृतम् = अधिकृतम्
6. अधि + लोकम् = अधिलोकम्
7. अधि + वचनम् = अधिवचनम्
8. अधि + स्था = अधितिष्ठति
9. अधि + भारः = अधिभारः
10. अधि + पतिः = अधिपतिः
11. अधि+ अक्षः = अध्यक्षः
12. अधि + दैवतम् = अधिदैवतम्
13. अधि+ हरिः = अधिहरिः
14. अधि + स्थाता = अधिष्ठाता
15. अधि+ कृत्य = अधिकृत्य
16. अधि + कारः = अधिकारः
17. अधि+ करणम् = अधिकरणम्
18. अधि + कारी = अधिकारी
19. अधि+ क्षेपः = अधिक्षेपः
20. अधि + शेषः = अधिशेषः

अभ्यासः

प्रश्न 1.
अधोलिखित प्रश्नानाम् उचित विकल्पं चित्वा लिखत –
1. ‘अप’ उपसर्गयुक्तं शब्दः कः नास्ति?
(अ) अपशब्दः
(ब) अपेक्षा
(स) अवगुणः
(द) अपव्ययः
उत्तरम् :
(अ) अपशब्दः

2. ‘आनयति’ इति पदे कः उपसर्गः ?
(अ) निर्
(ब) अप्
(स) नी
(द) आ
उत्तरम् :
(ब) अप्

3. ‘निस्’ उपसर्गयुक्तं शब्दः कः अस्ति?
(अ) निर्वेदः
(ब) निर्धनः
(स) निष्प्राणः
(द) नियमः
उत्तरम् :
(ब) निर्धनः

4. ‘निष्कामति’ इति पदे : उपसर्ग:?
(अ) उद्
(ब) दुर्
(स) निस्
(द) निर्
उत्तरम् :
(ब) दुर्

5. ‘आङ’ उपसर्गयुक्तं शब्दः कः अस्ति?
(अ) अपव्ययः
(ब) अपशब्दः
(स) अवगुणः
(द) अपेक्षा
उत्तरम् :
(स) अवगुणः

6. ‘निरीक्षणम्’ इति पदे कः उपसर्गः?
(अ) निस्
(ब) दुर्
(स) निर्
(द) आङ
उत्तरम् :
(अ) निस्

7. ‘दुर्’ उपसर्गयुक्तं शब्दः कः नास्ति?
(अ) दुराशा
(ब) दूरम्
(स) दुर्जनः
(द) दुर्बलः
उत्तरम् :
(स) दुर्जनः

8. ‘अध्यक्षः’ इति पदे कः उपसर्ग:?
(अ) अधि
(ब) अव
(स) आ
(द) अप्
उत्तरम् :
(ब) अव

9. ‘अव’ उपसर्गयुक्तं शब्दः कः नास्ति?
(अ) अवागच्छत्
(ब) अवकाशः
(स) अवतिष्ठति
(द) अवनि
उत्तरम् :
(स) अवतिष्ठति

10. ‘उत्’ उपसर्गयुक्तं शब्दः कः अस्ति?
(अ) उपदेशः
(ब) उत्थानम्
(स) उपकारः
(द) उपेक्षा
उत्तरम् :
(अ) उपदेशः

प्रश्न 2.
निम्नलिखित उपसर्गम् शब्दम् च योगेन सार्थक शब्द रचनां कृत्वा रिक्तस्थान पूरयत –
पदम् उपसर्ग + शब्द
(i) दुर् + आशा ……………………..
(ii) दुर् + भाग्यम् ……………………..
(iii) आ + कर्षणम् ……………………..
(iv) आ + गमनम् ……………………..
(v) आ + दानम् ……………………..
उत्तरम् :
(i) दुराशा,
(ii) दुर्भाग्यम्,
(iii) आकर्षणम्,
(iv) आगमनम्,
(v) आदानम्।

प्रश्न 3.
निम्नाङ्किताभ्यामुपसर्गधातुभ्यां क्रियापदं रचयत –
(क) अव + तृ
(ख) अप + कृ।
उत्तरम् :
(क) अवतरति
(ख) अपकरोति।

प्रश्न 4.
निम्नलिखितपदयोः प्रयुक्तमुपसर्गयोः लिखत –
(क) अपकर्षः
(ख) निर्जनम्।
उत्तरम् :
(क) अप
(ख) निर्।

प्रश्न 5.
निम्नलिखितपदयोः प्रयुक्तमुपसर्गं लिखत –
(क) निर्गच्छति,
(ख) निष्क्रामति।
उत्तरम् :
(क) निर्
(ख) निस्।

प्रश्न 6.
निम्नलिखिताभ्यामुपसर्गधातुभ्यां क्रियापदं रचयत –
(क) आ + नी
(ख) निर् + गम्।
उत्तरम् :
(क) आनयति
(ख) निर्गच्छति।

प्रश्न 7.
निम्नलिखित उपसर्गधातुभ्यां क्रियापदं रचयत –
(क) उत् + स्था
(ख) अधि + कृ।
उत्तरम् :
(क) उत्तिष्ठति
(ख) अधिकरोति।

प्रश्न 8.
निम्नलिखितपदयोः प्रयुक्तमुपसर्गयोः लिखत –
(क) उन्नति
(ख) अध्यक्षः।
उत्तरम् :
(क) उत्
(ख) अधि।

प्रश्न 9.
निम्नलिखितपदयोः प्रयुक्तमुपसर्ग लिखत –
(क) निर्वृत्तिः
(ख) अवरोहति।
उत्तरम् :
(क) निर्
(ख) अव।

प्रश्न 10.
निम्नलिखिताभ्यामुपसर्गधातुभ्यां क्रियापदं रचयत –
(क) अप + हृ
(ख) निस् + सृ।
उत्तरम् :
(क) अपहरति
(ख) निस्सरति।

प्रश्न 11.
निम्नलिखित उपसर्गधातुभ्यां क्रियापदं रचयत
(क) अव + गम्
(ख) निस् + सृ।।
उत्तरम :
(क) अवगच्छति
(ख) निस्सरति।

प्रश्न 12.
निम्नलिखितपदयोः प्रयुक्तमुपसर्ग लिखत –
(क) दुर्लभते
(ख) उत्तिष्ठतु।
उत्तरम् :
(क) दुर्
(ख) उत्।

प्रश्न 13.
अधोलखितपदेषु उपसर्गम् धातुम् च पृथक् कृत्वा लिखत।

प्रश्न 14.
निम्नलिखितानाम् उपसर्गाणां धातूनां च योगेन सार्थकशब्दरचनां कुरुत।

प्रश्न 15.
निम्नलिखितपदेषु प्रयुक्तान् उपसर्गान् लिखत।

प्रश्न 16.
अधोलखितपदेषु उपसर्गम् धातुम् च पृथक् कृत्वा लिखत।

प्रश्न 17.
निम्नलिखितानाम् उपसर्गाणां धातूनां च योगेन सार्थकशब्दरचनां कुरुत।

प्रश्न 18.
निम्नलिखितपदेषु प्रयुक्तान् उपसर्गान् लिखत।

प्रश्न 19.
निम्नलिखितपदेषु उपसर्ग शब्दं च पृथक् कृत्वा लिखत।

प्रश्न 20.
निम्नलिखितपदेषु उपसर्ग शब्दं च पृथक् कृत्वा लिखत।

प्रश्न 21.
निम्नलिखितानाम् उपसर्गाणां धातूनां च योगेन सार्थकशब्दरचनां कुरुत।

प्रश्न 22.
निम्नलिखितानाम् उपसर्गाणां धातूनां च योगेन सार्थकशब्दरचनां कुरुत।

प्रश्न 23.
निम्नलिखितपदेषु उपसर्ग शब्दं च पृथक् कृत्वा लिखत।

Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् अव्ययपदानि Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् अव्ययपदानि

संस्कृतभाषायां शब्दप्रकारद्वयमस्ति – विकारी अविकारी च। ये शब्दः विभक्तिप्रत्यय-उपसर्गः मिलित्वा रूपपरिवर्तनं कुर्वन्ति ते ‘विकारी’ इति शब्देन निर्दिश्यन्ते। अविकारिणः तु कदापि रूपपरिवर्तनं न कुर्वन्ति। एते ‘अव्यय’-शब्देन कथ्यन्ते। अर्थात् येषु शब्देषु लिङ्गवचनकारकादि-सम्बन्धेन रूपपरिवर्तनां न भवति ते अव्ययानि सन्ति। उक्तं च-(संस्कृत भाषा में शब्द के दो प्रकार हैं- विकारी और अविकारी। जो शब्द विभक्ति-प्रत्यय-उपसर्ग से मिलकर रूप परिवर्तन करते हैं वे ‘विकारी’ इस शब्द से निर्देशित किये जाते हैं। अविकारी तो कभी भी रूप परिवर्तन नहीं करते हैं। ये अव्यय शब्द कहे जाते हैं। अर्थात् इन शब्दों में लिङ्ग, वचन, कारक आदि के सम्बन्ध से रूप परिवर्तन नहीं होता है, वे अव्यय पद हैं। जैसा कि कहा है-)

सदृशं त्रिषु लिङ्गेषु सर्वासु स विभक्तिषु।
वचनेषु च सर्वेषु यन्त्र व्येति तदव्ययम्।।

अव्ययानां अन्ते आगतानां र-स्-वर्णानां स्थाने विसर्गः प्रयुज्यते यथा-उच्चैस-उच्चैः, नीचैस नीचैः, अन्तर=अन्त: पुनर-पुनः इति। (अव्ययों के अन्त में आये हुए ‘र’ और ‘स्’ वर्गों के स्थान पर विसर्ग प्रयुक्त किया जाता है जैसे-उच्चैस्-उच्चैः, नीचैस्-नीचैः, अन्तर्-अन्तः, पुनर्=पुनः आदि।)

अव्ययानामपि प्रकार द्वयमस्ति – प्रथमं तावत् रूढ़म्, अव्युत्पन्न वा। यथा-च, वा, विना, पृथगादीनि धातोः अव्युत्पन्नानि। द्वितीयं यौगिकं व्युत्पन्नं वा। यथा पठित्वा, पठितुमादीनि धातोः व्युत्पन्नानि कृदन्दताव्ययानि। सर्वदा, चतुर्धादीनि नाम्न: व्युत्पन्नानि तद्विताव्ययानि च। तद्धिताव्ययानां भेदा अपि सन्ति। यथा- (अव्ययों के दो प्रकार हैं- पहला अधिकार रूढम् अथवा अव्युत्पन्नम् है। जैसे- च, वा, विना, पृथगादीनि धातु से अव्युत्पन्न हैं। दूसरा अधिकार यौगिक अथवा व्युत्पन्न है। पठितुम् आदि धातु से व्युत्पन्न कृदन्त अव्यय हैं। और सर्वदा, चतुर्धा आदि नाम से व्युत्पन्न तद्धित अव्यय हैं। तद्धित अव्ययों के भेद भी हैं। जैसे-)

विभक्ति बोधकानि – कुतः, ग्रामतः, कुत्र अत्रादीनि।
कालबोधकानि – यदा, कदा, सर्वदादीनि।
प्रकारबोधकानि – यथा, तथा, कथम्, इत्थम्, द्वेधादीनि।
विविधानि – अनेकशः पञ्चत्व आदीनि।

अत्र केषाञ्चिदव्ययानां अर्थोः उदाहरणानि च प्रस्तूयन्ते- (यहाँ कुछ अव्ययों के अर्थ और उदाहरण प्रस्तुत किये जा ‘ रहे हैं-)

ध्यातव्यम् –
अव्ययानां पञ्च भेदा सन्ति (अव्ययों के पाँच भेद हैं-)
(i) क्रिया-विशेषण
(ii) सम्बन्धबोधक
(iii) समुच्चयबोधकः
(iv) विस्मयादिबोधकः
(v) उपसर्गाः।

1. क्रिया-विशेषण अव्यय – जो अव्यय शब्द क्रिया की विशेषता बतलाते हैं, उन्हें क्रिया-विशेषण अव्यय कहा जाता है। इन्हें मुख्यतः तीन भागों में विभाजित किया जा सकता है – (i) कालवाचक (ii) स्थानवाचक (ii) रीतिवाचक (iii) रीतिवाचक क्रियाविशेषण।

2. सम्बन्धबोधक अव्यय – जो अव्यय शब्द संज्ञा, सर्वनाम आदि शब्दों के सम्बन्ध का बोध कराते हैं, उन्हें सम्बन्धबोधक अव्यय कहते हैं। यथा
(i) नगरस्य मध्ये एव चिकित्सालयः अस्ति। (नगर के मध्य ही चिकित्सालय है।)
(ii) ग्रामस्य समीपे एव नदी प्रवहति। (गाँव के समीप ही नदी बहती है।) यहाँ ‘मध्ये’ और ‘समीपे’ सम्बन्धबोधक अव्यय हैं।

3. समुच्चयबोधक अव्यय-जो अव्यय शब्द दो पदों या वाक्यों को परस्पर जोड़ने का काम करते हैं, उन्हें समुच्चय– बोधक अव्यय कहते हैं। जैसे-च (और) वा (अथवा) आदि।
(i) सुरभितः शीतलः च पवन: वहति। (सुगन्धित और शीतल हवा चल रही है।)
(i) महेशः दिनेशः वा गायति। (महेश अथवा दिनेश गा रहा है।)

4. विस्मयादिबोधक अव्यय-जो अव्यय शब्द हर्ष, विषाद, सम्बोधन, दुःख, खेद, घृणा, आश्चर्य, आशीर्वाद, भय, लज्जा आदि भावों या मनोविकारों को प्रकट करते हैं, उन्हें विस्मयादिबोधक या मनोविकारसूचक अव्यय कहते हैं, जैसे –
आः, अहो, आम्, अहह, धिक्, हा, हन्त आदि।

(i) आ:! स्वयं मृतोऽसि। (अरे! स्वयं मर गये हो।)
(ii) अहो ! देशस्य दुर्भाग्यम्। (अरे! देश का दुर्भाग्य।)
(iii) अहो ! बलीयः खलु भीतोऽस्मि। (अरे ! बहुत अधिक डर गया हूँ।)।

5. उपसर्ग अव्यय-उपसर्ग वे अव्यय शब्दांश हैं जो क्रियादि पदों से पूर्व जुड़कर उनके अर्थ को बदल देते हैं या उसमें कुछ विशेषता ला देते हैं। ये प्र आदि 22 होते हैं अत: इन्हें ‘प्रादयः’ कहते हैं। इनका अपना कोई अर्थ या स्वतन्त्र प्रयोग नहीं होता। ये हैं – प्र (अधिक), परा (पीछे), अप (दूर), सम् (अच्छी तरह), अनु (पीछे), अव (दूर, नीचे), निस् (बिना), निर् (बाहर), दुस् (कठिन), दुर् (बुरा), वि (बिना), आङ् (तक), नि (नीचे), अधि (ऊपर), अपि (भी), अति (बहुत), सु (अच्छा), उद् (ऊपर), अभि (ओर), प्रति (ओर, उल्टा), परि (चारों ओर), उप (निकट)। यथा – प्रणामः, पराजयः, अपमानः, संयोगः, अनुरागः, अवमानना, निस्सन्देहः, निराकारः, दुस्साहसः, दुर्जयः, वियोगः, आवासः, निरोधः, अधिकारः, अपिधानम् (पिधानम्), अतिक्रमणम्, सुभगः, उत्थानम्, अभिमानम्, प्रत्युत्तरम्, परितः, उपयोगः।
नोट – उपर्युक्त स्थूलांकित शब्दांश उपसर्ग हैं।

अभ्यासः

प्रश्न 1.
अधोलिखित प्रश्नानाम् उचित विकल्पं चित्वा लिखत –
1. ……………. स्वर्णमयी लङ्का लक्ष्मण मे न रोचते।
(अ) अपि
(ब) इति
(स) इव
(द) एव
उत्तरम् :
(अ) अपि

2. तस्य स्वत्वं. ……….. राष्ट्रे भवितुं न किलार्हति।
(अ) तु
(ब) तत्र
(स) कुत्र
(द) यत्र।
उत्तरम् :
(ब) तत्र

3. स्थाने खलु ऋषिजनेन सर्वदमन ……………. कृतनामधेयोऽसि।
(अ) अपि
(ब) इति
(स) यत्
(द) तत्र
उत्तरम् :
(ब) इति

4. ……………. वा मम माता?
(अ) तत्र
(ब) कुत्र
(स) तत्र
(द) यत्
उत्तरम् :
(ब) कुत्र

5. प्रतापस्य राज्ये ………….. जनक्षतिः धनक्षति च सजाता।
(अ) एवं
(ब) यत्
(स) अपि
(द) इति
उत्तरम् :
(स) अपि

6. ……………. तु मातुः सहयोगाय वीरमा गोचारण कार्यमारभत।
(अ) इदानीम्
(ब) अत्र
(स) इति
(द) एन
उत्तरम् :
(अ) इदानीम्

7. अयं पुनः गण्डस्योपरि पिटकः संवृत्तः…………….भयङ्करो दुर्भिक्षकालः समापन्नः।
(अ) इति
(ब) अपि
(स) यत्
(द) एव
उत्तरम् :
(स) यत्

8. ……………. केनापि कृपालना अनाथालये प्रवेशितः।
(अ) यत्र
(ब) तत्र
(स) अत्र
(द) कुत्र
उत्तरम् :
(ब) तत्र

9. ……………. तस्य हृदि संस्कृताध्ययनेच्छा।
(अ) तत्र
(ब) यत्र
(स) अत्र
(द) अपि
उत्तरम् :
(स) अत्र

10. जिज्ञासे सति कथितं ……………. जाटस्य तव संस्कृतं क्व सुलभम्?
(अ) यतः
(ब) यत्
(ब) चेत्।
(स) इति
उत्तरम् :
(अ) यतः

प्रश्न 2.
अधोलिखिताव्ययपदेषु उचितमव्ययपदं चित्वा रिक्त-स्थानं पूरयत।
(निम्न अव्यय पदों में से उचित अव्यय चुनकर रिक्त-स्थान की पूर्ति कीजिए।)
(क) शिखराणि ……………… लताभिः पुष्पिताग्रामिरूपगूढानि। (पुरुतः/सर्वतः)
(ख) वीरो …………….गर्वित कुञ्जस्थः। (तथा/यथा)
(ग) बोधिसत्वः …………. कस्मिंश्चित् सरसि मत्स्याधिपतिः बभूव। (किल/खलु)
(घ) वर्षनिवृत्ति साशङ्कः …………….. पर्जन्यमाबभाषे। (मुहुर्मुहुः पुनः पुनः)
(ङ) तवैव …………….. एषः सत्यातिशयप्रभावः। (किल/खलु)
(च) सः नैव स्त्री न …………. पुमान्। (ततः/पुनः)
(छ) हा ……………… ! अयमपि नाम परसम्पत्त्या सन्तप्यते ? (धिक्/हन्त)
(ज) हम्मीरदेवेन ……………… युद्धं कृतवान्। (साकं/प्रति)
(झ) महिमासाहिना ………….. त्वामनतकपरं नेष्यामि। (पुर:/सद्)
(ब) ………… परश्वोः वा दुर्गं ग्राहमिषवः। (ह्य/श्व:)
(ट) यवनराजेन ……………… योत्स्यामि। (सम/प्रति)
(ठ) यूयं सर्वे दुर्गाद् …………….. स्थानान्तरं गच्छत। (अन्तः/बहिः)
(ड) ………………… अलावरीनो नाम यवनराजो बभूव। (कुत्र/तत्र)
(ढ) पलायनमयि नोचितं (ततः/यतः)
(ण) नो चेदितो ………………. गच्छामि। (यत्र/अन्यत्र)
(त) यवनराजेन हम्मीरदेवं ………… दूतः प्रहितः। (प्रति/यदि)
(थ) …………… एनं न दास्यति तदा श्वस्तने तव दुर्गं विनशिष्यामि। (यदि/तदा)
(द) ………… निर्भसिते दूते गते। (यत:/ततः)
उत्तराणि :
(क) सर्वतः
(ख) यथा
(ग) किल
(घ) पुनः पुनः
(ङ) खलु
(च) पुनः
(छ) धिक्
(ज) साकम्
(झ) सह
(ज) श्वः
(ट) समम्
(ठ) बहिः
(ड) तत्र
(ढ) यतः
(ण) अन्यत्र
(त) प्रति
(थ) यदि
(द) ततः।

प्रश्न 3.
उचितेन अव्ययपदेन रिक्त-स्थानं पूरयत। (उचित अव्यय पद से रिक्त-स्थान की पूर्ति कीजिये।)
(क) मयि जीवति यमः ……………….. त्वां पराभवितुं न शक्नोति।
(ख) हम्मीरदेवेन साकं युद्धं कृतवान् ………………….. जयं न लब्धवान्।
(ग) यद्येनं न दास्यति …………………… श्वस्तने प्रभाते तव दुर्गं नाशयिष्यामि।
(घ) श्वः ………. वा दुर्गं ग्राहयिष्यावः।
(ङ) किञ्च यदि मन्यसे ……. निर्भय स्थानं त्वां प्रापयामि।
(च) ………………. एव क्रीडित्वा सोऽपि समागतः।
(छ) स्वामिन्याः …………………. भविष्यति।
(ज) कियद्वारं निर्दिष्टोऽसि ……………. प्रवचनं न कार्यम्।
(झ) अद्यागत ……………… एव वात्याचक्रमुत्थापयसि।
(ब) तव पिता …………… किं करोति ?
उत्तराणि :
(क) अपि
(ख) परं
(ग) तदा
(घ) परश्वः
(ङ) तदा
(च) इदानीम्
(छ) पार्वे
(ज) यत्
(झ) प्राय
(ब) च।

प्रश्न 4.
मञ्जूषायां प्रदत्तैः अव्ययपदैः रिक्तस्थानानि पूरयित्वा उत्तरपुस्तिकायां लिखत –
(मञ्जूषा में दिये हुए अव्यय पदों से रिक्त-स्थानों की पूर्ति करके उत्तर-पुस्तिका में लिखिए -)

1. तावत्, यत्र, तत्र, यदा, श्वः ह्यः, पुरा
(क) ह्यः सोमवासरः आसीत …………… बधवासरः भविष्यति।
(ख) …………. त्वम् आगमिष्यसि तदा अहम् आगमिष्यामि।।
(ग) यावत् त्वम् अत्र स्थास्यसि : ……………………… अहम् न आगमिष्यामि।
उत्तराणि :
(क) ह्यः सोमवासरः आसीत्, श्वः बुधवासरः भविष्यति।
(ख) यदा त्वम् आगमिष्यसि तदा अहम् आगमिष्यामि।
(ग) यावत् त्वम् अत्र स्थास्यसि तावत् अहं न आगमिष्यामि।

2. विना, सह, नूनम्, यदा, अधुना, अत्र, तत्र ।

रामः – अहं त्वां (i) …………. न गमिष्यामि।
मोहनः – किमर्थं मया एव (ii) …………. गमिष्यसि ?
रामः – (iii) ………….. रात्रिः अस्ति। अहम् अंधकारात् त्रस्यामि।
उत्तराणि :
रामः – अहं त्वां विना न गमिष्यामि।
मोहनः – किमर्थं मया एव सह गमिष्यसि ?
रामः – अधुना रात्रिः अस्ति। अहम् अंधकारात् त्रस्यामि।

3. किमर्थम्, तत्र, बहिर्, अधुना; इतस्ततः, कुतः, यत्।

नैतिक – गर्वित ! गृहाद् (i) ………… गत्वा उद्यानात् पुष्पाणि आनय।
गर्वित – भ्रातः ! अहं (i) ………… एकाकी न गमिष्यामि।
नैतिक – (iii) …………. एकाकी न गमिष्यसि।
उत्तराणि :
नैतिक – गर्वित ! गृहाद बहिर् गत्वा उद्यानात् पुष्पाणि आनय।
गर्वित – भ्रातः! अहं तत्र एकाकी न गमिष्यामि।
नैतिक – किमर्थम् एकाकी न गमिष्यसि ?

4. अन्यत्र, अपि, कुत्र, किमर्थम्, तदा, यदा, मा।

सीमा – सुरेखे! त्वं प्रभाते (i) ………… गच्छसि?
सुरेखा – अहं (ii) ………… भ्रमितुं गच्छामि।
सीमा – तिष्ठ, अहम् (iii) …………… त्वया सह चलिष्यामि।
उत्तराणि :
सीमा – सुरेखे! त्वं प्रभाते कुत्र गच्छसि ?
सुरेखा – अहं अन्यत्र भ्रमितुं गच्छामि।
सीमा – तिष्ठ, अहम् अपि त्वया सह चलिष्यामि।

5. तत्र, श्वः, ह्यः, कुत्र, यत्र, शनैः शनैः, इतस्ततः

राम – श्याम! सुनील: (i) …………… गतः ?
श्याम – (ii) …………. अहं तम् आपणे अपश्यम्।
राम – सः (iii) ………….. किं करोति स्म ?
उत्तराणि :
राम – श्याम! सुनील: कुत्र गतः ?
श्याम – ह्यः अहं तम् आपणे अपश्यम्।
राम – सः तत्र किं करोति स्म ?

6. इतस्ततः, मा, तावत्, बहिः, सहसा, यदा, तदा।।

(i) यावत् अहम् अत्र तिष्ठामि …………. मा गच्छ।
(ii) सिंहस्य अभावे वने जीवाः …………… भ्रमन्ति।
(iii) ………….. कदापि कार्याणि न कुर्यात्।
उत्तराणि :
(i) यावत् अहम् अत्र तिष्ठामि तावत् मा गच्छ।
(ii) सिंहस्य अभावे वने जीवाः इतस्ततः भ्रमन्ति।
(iii) सहसा कदापि कार्याणि न कुर्यात्।

7. एव, अलम्, उच्चैः, अधुना, शनैः, च, अपि।

अनिलः – आगतः अस्मि, श्रीमन्त: (i) ………… किं करवाणि ?
अध्यापकः – (ii) ………..” भ्रमणेन। अत्र उपविश।
अनिल: – आम्, उपविशामि। यद् भवन्तः कथयिष्यन्ति तद् (iii) ……….. …. करिष्यामि।
उत्तराणि :
अनिलः – आगतः अस्मि, श्रीमन्तः अधुना किं करवाणि ?
अध्यापकः – अलं भ्रमणेन। अत्र उपविश।
अनिलः – आम्, उपविशामि। यद् भवन्तः कथयिष्यन्ति तद् एव करिष्यामि।

8. अपि, पुरा, विना, बहिः, कुत्र, वृथा, शनैः।

भानुप्रिया – त्वम् अधुना (i) …………… गच्छसि ?
भानुप्रताप – अहं ग्रामाद (ii) …………… भ्रमणाय गच्छमि।
भानुप्रिया – अहम् (iii) …………. त्वया सह गन्तुम् इच्छामि।
उत्तराणि :
(i) कुत्र
(ii) बहिः
(iii) अपि

9. बहिः, एव, अपि, कुत्र, यत्र, तत्र, किमर्थम्।

माता – वत्स! एषः कोलाहलः (i) …………. भवति।
पुत्रः – मातः! (ii) …………… एकः अहितुण्डकः आयातः।
माता – एते अहितुण्डकाः सर्पान् (iii) ………….. प्रदर्शयन्ति।
उत्तराणि :
माता – वत्स ! एषः कोलाहलः कुत्र भवति।
पुत्रः – माता:! बहिर् एकः अहितुण्डकः आयातः।
माता – एते अहितुण्डकाः सर्पान् किमर्थं प्रदर्शयन्ति ?

10. ननु, नूनम्, एव, श्वः, अपि, खलु, तत्र

शिक्षकः – छात्राः! (i) …………. विद्यालये वृक्षारोपणं भविष्यति।
मोहनः – अहं गृहाद् (ii) …………… एकं पादपम् आनेष्यामि।
शिक्षकः – निर्मले! त्वम् (iii) …………… पादपम् आनेष्यति।
उत्तराणि :
शिक्षकः – छात्राः! श्वः विद्यालये वृक्षारोपणं भविष्यति।
मोहनः – अहं गृहाद् एव एक पादपम् आनेष्यामि।
शिक्षकः – निर्मले ! त्वम् अपि पादपम् आनेष्यति।

11. शनैः शनैः, इतस्ततः, तथा, यदा, यदि, अत्र, अपि।

अपूर्वः – (i) …………. एकं विशालम् उपवनम् अस्ति।
प्रत्यूषः – पश्य, वृक्षेषु वानराः (ii) ………… कूर्दन्ति।
अपूर्वः – तत्र तु मयूरा: (iii) …………… नृत्यन्ति।
उत्तराणि :
अपूर्वः – अत्र एक विशालम् उपवनम् अस्ति।
प्रत्यूषः – पश्य, वृक्षेषु वानराः इतस्ततः कूर्दन्ति।
प्रत्यूषः – तत्र तु मयूराः अपि नृत्यन्ति।

12. यथा, अलम्, इदानीम्, इतः

शिक्षकः – सचिन ! (i) …………..” आगच्छ।
सचिन – आगतः श्रीमन् (i) ………….. किं करणीयम्। भ्रमणाय गच्छामि।
शिक्षकः – (iii) ………… भ्रमणेन, पाठं स्मर।
उत्तराणि :
शिक्षकः – सचिन! इतः आगच्छ।
सचिन – आगतः श्रीमन् ! इदानीं किं करणीयम्। भ्रमणाय गच्छामि।
शिक्षक – अलं भ्रमणेन पाठं स्मर।

13. उच्चैः, अधुना, अद्य, ह्यः, बहिः, श्वः, तदा।

(क) विद्यालये ……….. वार्षिकोत्सवः अस्ति।
(ख) छात्राः विद्यालयात् ………… प्रवेशद्वारे अतिथीनां स्वागतं करिष्यन्ति।
(ग) केचन …………… जयघोषं करिष्यन्ति।
उत्तराणि :
(क) विद्यालये अध वार्षिकोत्सवः अस्ति।
(ख) छात्राः विद्यालयात् बहिः प्रवेशद्वारे अतिथीनां स्वागतं करिष्यन्ति।
(ग) केचन उच्चैः जयघोषं करिष्यन्ति।

14. ह्यः, मा, यत्र, विना, श्वः, अपि, एव।

(क) बालाः ……………… क्रीडन्ति, तत्र जनाः अपि भ्रमन्ति।
(ख) परिश्रमं ……………….. कुत्र साफल्यम् ?
(ग) भवन्तः ……………….. किमर्थं गमिष्यन्ति ?
उत्तराणि :
(क) बालाः यत्र क्रीडन्ति, तत्र जनाः अपि भ्रमन्ति।
(ख) परिश्रमं विना कुत्र साफल्यम् ?
(ग) भवन्तः श्वः किमर्थं गमिष्यन्ति ?

15. पुनः, इति, अपि, विना, ह्यः, इतस्ततः, उच्चैः।

(i) ………..” वयं जन्तुशालां द्रष्टुं काननवनम् अगच्छाम। सर्वे पशवः (i) ……………. भ्रमन्ति स्म। सिंहाः (ii) …………. गर्जन्ति स्म।
उत्तराणि :
ह्यः वयं जन्तुशालां द्रष्टुं काननवनम् अगच्छाम। सर्वे पशवः इतस्ततः भ्रमन्ति स्म। सिंहाः उच्चैः गर्जन्ति स्म।

16. विना, पुनः, एव, तत्र-तत्र, इति, शनैः, अतः

वस्तुत: मयूरं (i) …………. कुत्र जन्तुशालायाः शोभा। तत्र आम्रवृक्षाः आसन् (i) …………. कोकिलाः अपि आसन्। यत्र-यत्र आम्रवृक्षाः (iii) ………….. कोकिला: तु भविष्यन्ति एव।
उत्तराणि :
वस्तुत: मयूरं विना कुत्र जन्तुशालायाः शोभा। तत्र आम्रवृक्षाः आसन् अतः कोकिलाः अपि आसन्। यत्र-यत्र आम्रवृक्षाः तत्र-तत्र कोकिला: तु भविष्यन्ति एव।

17. अधुना, सदैव, वृथा, एव, यत्र-यत्र, इव, नूनम्।।

ते जनाः (i) ……….. धन्याः, ये कदापि निरुत्साहिताः न भवन्ति। ते सदैव धन्याः, ये (ii) …………. न …………. वदन्ति। ते (iii) …………… गच्छन्ति, तत्र-तत्र सफलाः भवन्ति।
उत्तराणि :
ते जनाः नूनं धन्याः, ये कदापि निरुत्साहिताः न भवन्ति। ते सदैव धन्याः, ये वृथा न वदन्ति। ते यत्र-यत्र गच्छन्ति, तत्र-तत्र सफलाः भवन्ति।

18. सह, उच्चैः, बहिः, इतस्ततः, अपि, एव, शीघ्रम्।

नगरात् (i) ………….. एकं वनम् अस्ति। तत्र दिने (ii) …………… अन्धकारः भवति। जनाः प्रायः कुक्कुरैः (iii) ……….. एव तत्र प्रविशन्ति।
उत्तराणि :
नगरात् बहिर् एकं वनम् अस्ति। तत्र दिने अपि अन्धकारः भवति। जनाः प्रायः कुक्कुरैः सह एव तत्र प्रविशन्ति।

19. इतस्ततः, तत्र, परम्, विना, तु, ह्यः सदैव।

(i) ………….. वयं बुद्धोद्याने भ्रमितुम् अगच्छाम। जनाः तत्र (ii) …………… भ्रमन्ति स्म। (iii) …………… छात्राः पुस्तकानि अपठन्।
उत्तराणि :
ह्यः वयं बुद्धोद्याने भ्रमितुम् अगच्छाम। जनाः तत्र इतस्ततः भ्रमन्ति स्म। तत्र छात्राः पुस्तकानि अपठन्।

20. मा, इतस्ततः, उपरि, अधः, अद्य, विना, सर्वत्र।

(i) ………….. वने पशु महोत्सवः अस्ति। मञ्चस्य (ii) …………… वनराजः सिंहः तिष्ठति। आकाशे (iii) …………. मेघाः सन्ति।
उत्तराणि :
अद्य वने पशु महोत्सवः अस्ति। मञ्चस्य उपरि वनराजः सिंह: तिष्ठति। आकाशे सर्वत्र मेघाः सन्ति।

21. सहसा, उच्चै, एव, पुरा।

(i) …………. गायति सः गायकः। (ii) सदा सत्यम् विजयति। (iii) ………….. संस्कृतं जनभाषा आसीत्।
उत्तराणि :
(i) उच्चै। (ii) एव। (iii) पुरा।

22. बहिः, अपि, यथा, कुत्र।

(i) सः क्रीडति अहम् …………… क्रीडामि। (i) भवती …………… पठति। (iii) ………. गुरुः तथा शिष्यः।
उत्तराणि :
(i) अपि। (ii) कुत्र। (iii) यथा।

23. एव, सहसा, वृथा, बिना।

(i) ……….. विदधीत न क्रियाम्। (ii) क्रियां ………… नरः अकर्मण्यः भवति। (iii) कर्मणा …………. नरः पूज्यते।
उत्तराणि :
(i) सहसा। (ii) बिना। (iii) एव।

प्रश्न 5.
अधोलिखितानाम् अव्यय शब्दानां स्वरचित संस्कृत वाक्येषु प्रयोगं कुरुत।
(निम्नलिखित अव्यय शब्दों का स्वरचित संस्कृत वाक्यों में प्रयोग कीजिए।)
उच्चैः, शनैः, अधः, अद्य, ह्यः, सायं, चिरम्, ईषत्, तूष्णीम् सहसा, पुरा, नूनम्, भूयः, खलु, धिक्।
उत्तर :

1. बालकः दृश्यम् अवलोक्य उच्चैः हसति। (बालक दृश्य को देखकर जोर से हँसता है।)
2. कच्छपः शनैः शनैः चलति। (कछुआ धीरे-धीरे चलता है।)
3. वृक्षस्य अधः एव साधोः उटजम्। (वृक्ष के नीचे ही साधु की कुटिया है।)
4. अद्य अहं विद्यालयं न गमिष्यामि। (आज मैं विद्यालय नहीं जाऊँगा।)
5. ह्यः सत्यदेवः जयपुरम् अगच्छत्। (कल सत्यदेव जयपुर गया।)
6. सायंकाले खगाः स्व स्व नीडं प्रत्यागच्छन्ति। (सायंकाल पक्षी अपने-अपने घोंसले में आ जाते हैं।)
7. चिरं जीवतु रामः। (रमा चिरायु हों)
8. मह्यम् ईषद् जलं देहि। (मुझे थोड़ा जल दो।)
9. तूष्णीं भव नोचेदाचार्य निवेदयिष्यामि। (चुप हो जा नहीं तो आचार्य से कह दूँगा।)
10. सहसैव सः तत्र प्राप्तः। (अकस्मात् ही वह वहाँ पहुँच गया।)
11. पुरा आदिकविः वाल्मीकिः रामचरितमलिखत्। (पहले आदिकवि वाल्मीकि ने रामचरित लिखा।)
12. अद्य सः नूनम् आगमिष्यति। (आज वह अवश्य आयेगा।)
13. भूयो भूयः नमाम्यहम्। (मैं बार-बार नमस्कार करता हूँ।)
14. नीचैः विघ्न भयेन खलु न प्रारभ्यते। (नीच (अधम) लोगों द्वारा विघ्नों के भय के कारण निश्चय ही कार्य प्रारम्भ नहीं किया जाता है।)
15. धिक् मूर्खम्। (मूर्ख को धिक्कार है)

प्रश्न 6.
अधोलिखिताव्ययानामर्थं हिन्दीभाषायां लिखित्वा संस्कृत वाक्येषु प्रयोगं कुरुत।
(निम्न अव्ययों का हिन्दी में अर्थ लिखकर संस्कृत वाक्यों में प्रयोग कीजिए।
तथा, नीचैः, युगपत, मिथ्या, श्वः, अचिरम, पार्वे, किल, यत्र, यत्।
उत्तराणि :

• तथा – (वैसा) यथा मेघाः गर्जन्ति तथा एव जलं वर्षति। (जैसे मेघ गर्जते हैं वैसे ही जल बरसता है।)
• नीचैः – (धीमे) त्वं सर्वदा नीचैः एव वदसि। (तम हमेशा धीमे बोलते हो।)
• युगपत् – (एक साथ) चक्रेण युगपत्। (चक्र के साथ)
• मिथ्या – (झूठ) मिथ्या वचनं पापमूलम्। (मिथ्या वचन पाप का मूल है।)
• श्वः – (आने वाला कल) अहं श्वः एव विदेशं गमिष्यामि। (मैं कल ही विदेश जाऊँगा।)
• अचिरम् – (शीघ्र) अचिरमेव सः अरोदत्। (वह शीघ्र रो पड़ा)
• पार्श्वे – (पास, बगल में) मातुः पार्वे भविष्यति। (माँ के पास होगा।)
• किल – (निश्चय, अवश्य ही) गायन्ति देवाः किल गीतकानि। (निश्चित ही देवता गीत गाते हैं।)
• यत्र – (जहाँ) सः तत्र गच्छति यत्र त्वं गच्छसि। (वह वहाँ जाता है जहाँ तू जाता है।)
• यत् – (कि) अहं जानामि यत् त्वं मूर्योऽसि। (मैं जानता हूँ कि तुम मूर्ख हो)।

Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् प्रत्ययज्ञानम् Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् प्रत्ययज्ञानम्

प्रत्ययस्य परिभाषा – धातोः प्रातिपादिकस्य वा पश्चात् यस्य प्रयोगः क्रियते सः प्रत्ययः इति कथ्यते। (धातु अथवा प्रातिपदिक (शब्द) के पश्चात् जिसका प्रयोग किया जाता है वह प्रत्यय कहा जाता है।)

प्रत्यानां भेदाः – प्रत्ययानां मुख्यरूपेण त्रयो भेदाः सन्ति। ते क्रमशः इमे सन्ति- (प्रत्ययों के मुख्य रूप से तीन भेद हैं। जो क्रमश: ये हैं-)

1. कृत् प्रत्ययाः
2. तद्धितप्रत्ययाः
3. स्त्रीप्रत्ययाः

1. कृत-प्रत्ययाः – येषां प्रत्ययानां प्रयोगः धातोः (क्रियायाः) पश्चात् क्रियते ते कृत् प्रत्ययाः कथ्यन्ते। यथा- (जिन प्रत्ययों का प्रयोग धातु (क्रिया) के पश्चात् किया जाता है वे कृत् प्रत्यय कहे जाते हैं। जैसे -)

कृ + तव्यत् = कर्त्तव्यम् = करना चाहिए।
पठ् + अनीयर् = पठनयीम् = पढ़ना चाहिए।

2. तद्धितप्रत्ययाः – येषां प्रत्ययानां प्रयोगः संज्ञासर्वनामादिशब्दानां पश्चात् क्रियते ते तद्धितप्रत्ययाः कथ्यन्ते। यथा (जिन प्रत्ययों का प्रयोग संज्ञा, सर्वनाम आदि शब्दों के पश्चात् किया जाता है वे तद्धित प्रत्यय कहे जाते हैं। जैसे-)

शिव + अण् = शैवः।
उपगु + अण् = औपगवः
दशरथ + इञ् = दाशरथिः
धन + मतुप् = धनवान्

3. स्त्रीप्रत्ययाः – येषां प्रत्ययानां प्रयोगः पुंल्लिङ्गशब्दान् स्त्रीलिङ्गे परिवर्तयितुं क्रियते ते स्त्रीप्रत्ययाः कथ्यन्ते। यथा (जिन प्रत्ययों का प्रयोग पुँल्लिङ्ग शब्दों को स्त्रीलिङ्ग में परिवर्तित करने के लिये किया जाता है वे स्त्री प्रत्यय कहे जाते हैं। जैसे-)

कुमार + ङीप् = कुमारी
अज + टाप् = अजा

कृत-प्रत्ययाः

शतृप्रत्ययः
वर्तमानकालार्थे अर्थात् गच्छन् (जाते हुए), लिखन् (लिखते हुए) इत्यस्मिन् अर्थे परस्मैपदिधातुभ्यः शतृप्रत्ययः भवति। अस्य ‘अत्’ भागः अवशिष्यतेः शकारस्य ऋकारस्य च लोपः भवति। शतप्रत्ययान्तस्य शब्दस्य प्रयोगः विशेषणवत् भवति। अस्य पल्लिङ्गे पठत-वत, स्त्रीलिङ्गगे नदी-वत, नपंसकलिङ्गे च जगत-वत चलन्ति। (वर्तमान काल के अर्थ में ‘गच्छन्’ (जाते हुए), लिखन् (लिखते हुए) अर्थात् ‘हुआ’ अथवा ‘रहा’, ‘रहे’ इस अर्थ में (इस अर्थ का बोध कराने के लिए) परस्मैपदी धातुओं में ‘शत’ प्रत्यय होता है। जिसका (शतृ का) ‘अत्’ भाग शेष रहता है, शकार और ऋकार का लोप होता है। ‘शतृ’ प्रत्ययान्त शब्द का प्रयोग विशेषण की तरह होता है। इसके रूप पुंल्लिङ्ग में पठत्-वत्, स्त्रीलिङ्ग में नदी-वत् और नपुसंकलिङ्ग में जगत-वत् चलते हैं।)

शतप्रत्ययान्त-शब्दाः

शतृ प्रत्ययान्त अन्य उदाहरणानि पुँल्लिते (शतृ प्रत्ययान्त अन्य उदाहरण केवल पुँल्लिङ्ग में)

शानच् प्रत्ययः

वर्तमानकालार्थे आत्मनेपदिधातुभ्यः शानच् प्रत्ययः भवति। अस्य शकारस्य चकारस्य च लोपः भवति, ‘आन’ इति अवशिष्यते। शानच् प्रत्ययान्तरस्य शब्दस्य प्रयोगः विशेषणवत् भवति। अस्य रूपाणि पुंल्लिङ्गे रामवत्, स्त्रीलिङ्गे रमावत्, नपुंसकलिङ्गे च फलवत् चलन्ति ! (वर्तमानकाल के अर्थ में आत्मनेपदी धातुओं में शानच प्रत्यय होता है। इसके (शानच् के) शकार और चकार का लोप होता है। ‘अ’ यह शेष रहता है। शानच् प्रत्ययान्त शब्द का प्रयोग विशेषण की तरह होता है। इसके रूप पुल्लिङ्ग में राम-वत् स्त्रीलिङ्ग में रमा-वत्, और नपुंसकलिङ्ग में फल-वत् चलते हैं।)

शानच् प्रत्ययान्त-शब्दाः

शानच् प्रत्ययान्त अन्य उदाहरणानि (पुल्लिड़े) (अन्य उदाहरण केवल पुल्लिङ्ग में दिये जा रहे हैं।)

तव्यत्-प्रत्ययः

तव्यत् प्रत्ययस्य प्रयोग: हिन्दीभाषायाः ‘चाहिए’ अथवा ‘योग्य’ इत्यस्मिन् अर्थे भवति। अस्य ‘तव्य’ भागः अवशिष्यते, तकारस्य च लोपः भवति। अयं प्रत्ययः भाववाच्ये अथवा कर्मवाच्ये एव भवति। तव्यत्-प्रत्ययान्तशब्दानां रूपाणि पुँल्लिङ्गे रामवत्, स्त्रीलिङ्गे रमावत्, नपुंसकलिङ्गे च फलवत् चलन्ति। (तव्यत् प्रत्यय का प्रयोग हिन्दी भाषा के ‘चाहिए’ अथवा ‘योग्य’ इस अर्थ में होता है। इसका (तव्यत् का) ‘तव्य’ शेष रहता है और तकार का लोप होता है। यह प्रत्यय भाववाच्य में अथवा कर्मवाच्य में ही होता है। तव्यत् प्रत्ययान्त शब्दों के रूप पुंल्लिङ्ग में राम-वत्, स्त्रीलिङ्ग में रमा-वत् और नपुंसकलिङ्ग में फल-वत् चलते हैं।)

तव्यत् प्रत्ययान्त शब्दाः

तव्यत् प्रत्ययान्त अन्य उदाहरणानि केवल पुल्लिङ्गे (तव्यत् प्रत्ययान्त अन्य उदाहरण केवल पुंल्लिङ्ग में)

अनीयर्-प्रत्ययः

अनीयर् प्रत्ययः तव्यत् प्रत्ययस्य समानार्थकः अस्ति। अस्य प्रयोगः हिन्दीभाषायाः ‘चाहिए’ अथवा ‘योग्य’ इत्यर्थे भवति। अस्य ‘अनीय’ भागः अवशिष्यते, रेफस्य च लोपः भवति। अयं प्रत्ययः कर्मवाच्ये अथवा भाववाच्ये एव भवति। अनीयर्-प्रत्ययान्त-शब्दानां रूपाणि पुंल्लिङ्गे रामवत्, स्त्रीलिङ्गे रमावत्, नपुंसकलिङ्गे च फलवत् चलन्ति। (‘अनीयर्’ प्रत्यय ‘तव्यत्’ प्रत्यय का समानार्थक है। इसका प्रयोग हिन्दी भाषा के ‘चाहिए’ अथवा ‘योग्य’ इस अर्थ में होता है। इसका (अनीयर का) ‘अनीय’ भाग शेष रहता है और रेफ का लोप होता है। यह प्रत्यय कर्मवाच्य अथवा भाववाच्य में ही होता है। अनीयर् प्रत्ययान्त शब्दों के रूप पुंल्लिङ्ग में राम-वत्, स्त्रीलिङ्ग में रमा-वत् और नपुंसकलिङ्ग में फल-वत् चलते हैं।)

अनीयर्-प्रत्ययान्तशब्दाः

अनीयर् ग्रहणीयम् अनीयर प्रत्ययान्त अन्य उदाहरणानि केवल पुंल्लिने (अनीयर् प्रत्ययान्त अन्य उदाहरण केवल पुंल्लिङ्ग में)

क्तिन प्रत्यय-स्त्रियां क्तिन:

भाववाचक शब्द की रचना के लिए सभी धातुओं से ‘क्तिन’ प्रत्यय होता है। इसका ‘ति’ भाग शेष रहता है, ‘कृ’ और “न्’ का लोप हो जाता है। ‘क्तिन’ प्रत्ययान्त शब्द स्त्रीलिंग में ही होते हैं। इनके रूप ‘मति’ के समान चलते हैं।
उदाहरण –

ल्युट्-प्रत्ययः

भाववाचक शब्द की रचना के लिए सभी धातुओं से ल्युट् प्रत्यय जोड़ा जाता है। इसका ‘यु’ भाग शेष रहता है तथा ‘ल’ और ‘ट्’ का लोप हो जाता है। ‘यु’ के स्थान पर ‘अन’ हो जाता है। ‘अन’ ही धातुओं के साथ जुड़ता है। ल्युट्-प्रत्ययान्त शब्द प्रायः नपुंसकलिङ्ग में होते हैं। इनके रूप ‘फल’ शब्द के समान चलते हैं।

ल्युट्-प्रत्ययान्तशब्दाः

तृच् प्रत्ययः

कर्ता अर्थ में अर्थात् हिन्दी भाषा में ‘करने वाला’ इस अर्थ में धातु के साथ तृच् प्रत्यय होता है। इसका ‘तृ’ भाग शेष रहता है और ‘च्’ का लोप हो जाता है। तृच्-प्रत्ययान्त शब्दों के रूप तीनों लिंगों में चलते हैं।

कृ + तृच् = कर्तृ (कर्ता)
पा + तृच् = पातृ (पिता)
गम् + तृच् = गन्तृ (गन्ता)
हृ + तृच् = हर्तृ (हर्ता)
भृ + तृच् = भर्तृ (भर्ता)

अन्य उदाहरण –

2. तद्धित-प्रत्ययाः

मतुप् प्रत्ययः
‘तदस्य अस्ति’ (वह इसका है अथवा वाला) अथवा ‘अस्मिन्’ (इसमें) इत्यर्थे तद्धितस्य मतुप् प्रत्ययः भवति। अस्य ‘मत्’ भागः अवशिष्यते, उकारस्य पकारस्य च लोपो भवति। ‘मत्’ इत्यस्य स्थाने क्वचित् ‘वत्’ इति भवति। मतुप् प्रत्ययान्तशब्दानां रूपाणि पुंल्लिङ्गे भगवत्-वत्, स्त्रीलिङ्गे ई (ङीप्) प्रत्ययं संयोज्य नदीवत्, नपुंसकलिङ्गे च जगत्-वत् चलन्ति। (‘वह इसका है’ अथवा ‘वाला’ अथवा ‘इसमें’ इन अर्थों में तद्धित का ‘मतुप्’ प्रत्यय होता है। इसका (मतुप् का) ‘मत्’ शेष रहता है, और उकार तथा पकार का लोप होता है। ‘मत्’ के स्थान पर कहीं ‘वत्’ भी होता है। मतुप् प्रत्ययान्त शब्दों के रूप पुंल्लिङ्ग में ‘भगवत्-वत्’, स्त्रीलिङ्ग में ‘ई’ (ङीप्) प्रत्यय जोड़कर ‘नदीवत्’ और नपुंसकलिङ्ग में ‘जगत्-वत्’ चलते हैं।)
इदमत्र अवगन्तव्यम् (यहाँ इसको जान लेना चाहिए।)
“वत्’ इत्यस्य प्रयोगः प्रायः इयन्तशब्देभ्यः अथवा झकारान्तशब्देभ्यः भवति। यथा- (‘वत्’ इसका प्रयोग प्रायः झकारान्त शब्दों अथवा अकारान्त शब्दों में होता है जैसे-)
झयन्तेभ्यः – विद्युत् + मतुप् = विद्युत्वत्
अकारान्तेभ्य – धन + मतुप् = धनवत्
विद्या + मतुप् = विद्यावत्

‘मत्’ इत्यस्य प्रयोगः प्रायः झकारान्तशब्देभ्यः भवति। यथा- (‘मत्’ इसका प्रयोग प्रायः इकारान्त शब्दों के साथ होता है। जैसे-)
श्री + मतुप् – श्रीमत्
बुद्धि + मतुप् + बुद्धिमत्

मतुप् प्रत्ययान्तशब्दाः

2. इन्-ठन् प्रत्ययौ

‘अत इनिठनौ’ अकारान्ताद् प्रातिपदिकाद् ‘तदस्य अस्ति’ (वह इसका है) अथवा ‘अस्मिन्’ (इसमें) इत्यर्थे इनिठनौ प्रत्ययौ भवतः। (‘वह इसका है’ अथवा ‘इसमें’ इस अर्थ में अकारान्त प्रातिपदिक (संज्ञा शब्दों) से ‘इन्’-‘ठन्’ प्रत्यय होते हैं।)

इनि – प्रयोगकाले ‘इनि’ प्रत्ययस्य ‘इन्’ अवशिष्यते, स च प्रथमाविभक्त्यर्थके ‘सु’ प्रत्यये ‘इ’ रूपे परिवर्तते। यथा-दण्डम् अस्य अस्तीति = दण्ड + इन् = दण्डिन् सु = दण्डी। ठन्- प्रयोगकाले ‘ठन्’ प्रत्ययस्य ‘ठ’ इति शिष्यते। ठस्य स्थाने च ‘इक’ आदेश: “ठस्येकः” सूत्रेण जायते। (‘इनि’ के प्रयोग में ‘इनि’ प्रत्यय का ‘इन्’ शेष रहता है और वह प्रथमा विभक्ति के अर्थ में ‘स’ प्रत्यय ‘ई’ रूप में परिवर्तित हो जाता है। जैसे- ‘दण्डम्’ इसका होता है दण्ड + इन = दण्डिन् प्रथमा विभक्ति में ‘सु’ प्रत्यय लगने पर- ‘दण्डिन् + सु’ ‘सु’ ‘ई’ रूप में परिवर्तित होकर दण्डी यह रूप बना। ‘ठन्’ का प्रयोग करने में ‘ठन्’ प्रत्यय का ‘ठ’ शेष रहता है। ‘ठ’ के स्थान पर ‘इक’ आदेश ‘ठस्येक’ सूत्र से होता है।)
यथा- दण्डम् अस्य अस्तीति- दण्ड + ठन् (ठ) दण्ड + इक = दण्डिकाः। उदाहरणानि
(जैसे- ‘दण्डम्’ इसका होता है – दण्ड + ठन् (ठ) = दण्ड + इक = दण्डिकः। उदाहरण-)

3. स्व-तल प्रत्ययो- ‘तस्य भावस्त्वतली’- षष्ठीसमर्थात् प्रातिपदिकात् भाव इत्येतस्मिन्नर्थे त्व-तली प्रत्ययो भवतः। प्रयोगस्थलेषु त्व प्रत्ययान्तशब्दस्य रूपाणि फलवत् नपुंसकलिङ्गमनुसरन्ति। तथैव तल् प्रत्ययान्तशब्दस्य रूपाणि लतावत् स्त्रीलिङ्गे चलन्ति। यथा- (‘तस्य भावस्त्वतलौ’ षष्ठी से समर्थित प्रातिपदिक (संज्ञा शब्द) से भावाचक के अर्थ में त्व-तलौ प्रत्यय होते हैं।) अर्थात् भाववाचक संज्ञा बनाने के लिये किसी शब्द में त्व अथवा तल् (ता) प्रत्यय लगाते हैं।) प्रयोग स्थलों में ‘तव’ प्रत्ययान्त शब्द के रूप फल-वत् नपुंसकलिङ्ग में चलते हैं। उसी प्रकार ‘तल’ प्रत्यन्त शब्द के रूप लता-वत् स्त्रीलिङ्ग में चलते हैं। जैसे-)

3. स्त्री-प्रत्ययाः

टाप प्रत्ययः- ‘अजाद्यतष्टाप’- अजादिभ्यः अकारान्तेभ्यश्च प्रातिपदिकेभ्यः स्त्रियां टाप टाप्प्रत्ययान्तशब्दानां रूपाणि आकारान्ताः स्त्रीलिङ्गे रमा-वत् चलन्ति। यथा- (‘अजाद्यतष्टाप्’- अकारान्त पुंल्लिङ्ग शब्दों से स्त्रीलिङ्ग बनाने के लिए उनके आगे ताप् (आ) प्रत्यय होता है। अर्थात् भाववाचक एंत्रा बनाने के लिये किसी शब्द में त्व अथवा तल (ता) प्रत्यय लगाते हैं। प्रयोग स्थलों में ‘त्व’ प्रत्ययान्त शब्द के रूप में फल. -वत् नपुंसकलिङ्ग में चलते हैं। उसी प्रकार ‘तल’ प्रत्ययान्त शब्द के रूप लता-वत् स्त्रीलिंग में चलते हैं। जैसे-)

टाप-प्रत्ययान्तशब्देषु क्वचित् अकारस्य इकारः भवति। यथा – (टाप् प्रत्ययान्त शब्दों में कहीं अकार का इकार होता है। जैसे-)

2. गीप् प्रत्ययः – (1) ‘न्नेभ्यो गीप्’ – ऋन्त्रेभ्यो डीप् – नकारान्तेभ्यश्च प्रातिपादिकेभ्यः (शब्देभ्यः) स्त्रियाम् (स्त्रीलिओं) छीप् प्रत्ययो भवति। जीप् प्रत्ययस्य ‘ई’ अवशिष्यते। सामान्य-प्रयोगस्थले छात्रैः जीवन्ताः शब्दाः ईकारान्त-रूपेण स्मर्यन्ते। (‘अत्रेभ्यो जीप’ – प्रकारान्त और नकारान्त (पल्लिा ) शब्दों में स्त्रीलिज बनाने के लिए जीप (1) प्रत्यय होता है। डीप् प्रत्यय का ‘ए’ शेष रहता है। सामान्य प्रयोग स्थल में छात्रों द्वारा सीबत इकारान्त शब्दों के रूप में स्मरण किये जाते है।)

(ii) ‘उगितश्च’ – उगिदन्तात् प्रातिपादिकात् स्त्रियां ङीप् प्रत्ययो भवति। येषु प्रत्येषु ‘उ, ऋ लु’ इत्येतेषां वर्णानाम् इत्संज्ञकत्वे लोपः ज्ञातः ते उगित् प्रत्ययाः। तैः प्रत्ययैः ये शब्दाः निर्मिताः ते उगिदन्ताः शब्दाः प्रातिपादिकाः वा, तेभ्यः उगिदन्तेभ्यः स्त्रियां ङीप् प्रत्यय: स्यात्। (ऐसे प्रातिपादिकों से जिनमें उकार और ऋकार का लोप होता है (मतुप, वतुप, इयसु, तवतु, शत से बने हुए शब्दों से) स्त्रीलिङ्ग बनाने में ङीप् (ई) प्रत्यय होता है। जिन प्रत्ययों में ‘उ, ऋ, लु’ इन वर्गों की इत्संज्ञा होकर लोप हो जाता है वे ‘उगित’ प्रत्यय हैं। उन प्रत्ययों से जो शब्द निर्मित होते हैं वे उगिदन्त शब्द अथवा प्रातिपदिक होते हैं, उन उगिदन्तों से स्त्रीलिङ्ग बनाने के लिए डीप (ई) प्रत्यय होवे।)

(iii) ‘टिड्ढाणद्वयसज्दनज्मात्रच्तयप्टक्ठकञ्क्वरपः’ – टित्, ढ, अण, अब, द्वयसच्, दनच, मात्रच्, तयप्, ठक, ठ, कम्, क्वरप्, इत्येवमन्तेभ्यः अनुपसर्जनेभ्यः प्रातिपदिकेभ्यः स्त्रियां ङीप् प्रत्ययो भवति। उदाहरणानि- (टित्, ढ, अण, अञ् द्वयसच्, दनच, मात्र, तयप्, ठक्, ठञ्, कञ्, क्वरप् इनसे अन्त होने वाले शब्दों के अनन्तर स्त्रीलिङ्ग बनाने के लिए डीप (ई) प्रत्यय होता है। जैसे-)

(iv) ‘वयसि प्रथमे’ – प्रथमे वयसि वर्तमानेभ्यः उपसर्जनरहितेभ्यः अदन्तेभ्यः प्रातिपदिकेभ्यः स्त्रियां ङीप् प्रत्ययो भवति। उदाहरणानि- (प्रथम वयस् (अन्तिम अवस्था को छोड़कर) का ज्ञान कराने वाले अदन्त शब्दों के अन्तर स्त्रीलिङ्ग बनाने के लिए डीप (ई) प्रत्यय होता है। जैसे-)

(v) षिद्गौरादिभ्यश्च – (पा. सू.)- जहाँ ‘ष’ का लोप हुआ हो (षित्) तथा गौर, नर्तक, नट, द्रोण, पुष्कर आदि गौरादिगण में पठित शब्दों से स्त्रीलिंग में ङीष् (ई) प्रत्यय होता है। यथा –
गौरी, नर्तकी, नटी, द्रोणी, पुष्करी, हरिणी, सुन्दरी, मातामही, पितामही, रजकी, महती आदि।

(vi) द्विगो:- द्विगुसंज्ञाकाद् अनुपसर्जनाद् अदन्तात् प्रातिपदिकात स्त्रियां ङीप् प्रत्ययो भवति।
अयमर्थः – अदन्ताः ये द्विगुसंज्ञकाः शब्दः तेभ्यः स्त्रीलिङ्गे ङीप् प्रत्ययः स्यात्। उदाहरणानि
(अदन्त जो द्विगुसंज्ञक शब्द हैं उनसे स्त्रीलिङ्ग में (स्त्रीलिङ्ग बनाने के लिए) ङीप् प्रत्यय होता है। जैसे-)

(vii) पुंयोगादाख्यायाम-पुरुषवाचक अकारान्त शब्द प्रयोग से स्त्रीलिंग हो तो उससे ङीष् (ई) हो जाता है। यथा गोपस्य स्त्री – गोप + ई = गोपी, शूद्रस्य स्त्री – शूद्र + ई = शूद्री।

(viii) जातेश्रस्त्रीविषयादयोपधात्-जो नित्य स्त्रीलिंग और योपध नहीं है, ऐसे जातिवाचक शब्द से स्त्रीलिंग में ङीष् होता है। ङीष् का भी ‘ई’ शेष रहता है। यथा –
ब्राह्मण + ई = ब्राह्मणी, मृग – मृगी, महिषी, हंसी, मानुषी, घटी, वृषली आदि।

(ix) इन्द्रवरुणभवशर्व० – इन्द्र आदि शब्दों से स्त्रीलिंग बनाने पर अनुक् (आन्) और ङीष् (ई) प्रत्यय होता है। यथा –
इन्द्र की स्त्री-इन्द्र + आन् + ई = इन्द्राणी, वरुण-वरुणानी, भाव-भवानी, शर्व-शर्वाणी, मातुल-मातुलानी, रुद्र-रुद्राणी, आचार्य-आचार्यानी आदि।

(x) यव’ शब्द से दोष अर्थ में, यवन शब्द से लिपि अर्थ में तथा अर्य एवं क्षत्रिय शब्द से स्वार्थ में आनुक् (आन्) और ङीष् (ई) होता है। जैसे –
यव + आन् + ई = यवानी, यवन + आन् + ई = यवनानी।
मातुलानी, उपाध्यायानी, आर्याणी, क्षत्रियाणी-इनमें भी स्त्री अर्थ में ङीष् होता है।

(xi) हिमारण्ययोर्महत्त्वे – महत्त्व अर्थ में हिम और अरण्य शब्द से ङीष् और आनुक् होता है। यथा महद् हिम-हिम + आन् + ई = हिमानी। (हिम की राशि) महद् अरण्यम् अरण्यानी (विशाल अरण्य)

(xii) वोतो गुणवचनात् – गुणवाचक उकारान्त शब्दसे स्त्रीलिंग बनाने के लिए विकल्प से ङीष् (ई) प्रत्यय होता है। यथा
मृदु से मृद्वी, पटु से पट्वी, साधु से साध्वी।

(xiii) इतो मनुष्यजाते: – इदन्त मनुष्य जातिवाचक शब्द से स्त्रीलिंग बनाने पर ङीष् (ई) होता हैं जैसे दाक्षि + ई = दाक्षी (दक्ष के पुत्र की स्त्री)

(xiv) बहु आदि शब्दों से, शोण तथा कृत्प्रत्ययान्त इकारान्त शब्दों से तथा नासिका-उत्तरपद वाले शब्दों से विकल्प से ङीष् प्रत्यय होता है। यथा –

अभ्यासः

प्रश्न 1.
प्रदत्तेषु उत्तरेषु प्रत्ययानुसार यत् उत्तरम् शुद्धम् अस्ति, तत् चित्वा लिखत –
(दिए गये उत्तरों में प्रत्यय के अनुसार जो उत्तर शुद्ध हो, उसे चुनकर लिखिए)
1. गुरवः ……………. (वन्द् + अनीयर)
(अ) वन्दनीयः
(ब) वन्दनीयम्
(स) वन्दनीयाः
(द) न कोऽपि
उत्तरम् :
(अ) वन्दनीयः

2. मानवसेवां ……………. (कृ + शानच्) वृक्षाः केषां न हितकराः।
(अ) कुर्वाणः
(ब) कुर्वाणाः
(स) कुर्वाणा
(द) न कोऽपि
उत्तरम् :
(अ) कुर्वाणः

3. ……………. (छाया + मतुप्) वृक्षाः आश्रयं यच्छन्ति।।
(अ) छायावान्
(ब) छायावन्तौ
(स) छायावन्तः
(द) न कोऽपि (कोकिल + टाप्)
उत्तरम् :
(स) छायावन्तः

4. ……………. आम्रवृक्षे मधुरं गायति।
(अ) कोकिला
(ब) कोकिले
(स) कोकिला:
(द) न कोऽपि
उत्तरम् :
(अ) कोकिला

5. ……………. (बल + इन) निर्बलान् रक्षन्ति।
(अ) बलिन्
(ब) बलिनी
(स) बलिनः
(द) न कोऽपि
उत्तरम् :
(स) बलिनः

6. अस्माभिः परस्परं स्नेहेन ……………. (वस् + तव्यत्)।
(अ) वसितव्यः
(ब) वसितव्या
(स) वसितव्यम्
(द) न कोऽपि
उत्तरम् :
(स) वसितव्यम्

7. उद्यमस्य ……………. (महत् + त्व) सर्वविदितम् एव।
(अ) महत्त्वः
(ब) महत्त्वम्
(स) महत्त्वा
(द) न कोऽपि
उत्तरम् :
(ब) महत्त्वम्

8. ……………. (वर्ष + ठक् + ङीप) परीक्षा समीपम् एव।
(अ) वार्षिकी
(ब) वार्षिकी
(स) वार्षिकम्
(द) न कोऽपि
उत्तरम् :
(अ) वार्षिकी

9. त्वं कर्त्तव्यनिष्ठः ……………. (अधिकार + इन्) असि।
(अ) अधिकारी
(ब) अधिकारिन्
(स) अधिकारिणी
(द) न कोऽपि
उत्तरम् :
(अ) अधिकारी

10. छात्रैः अनुशासनम् ……………. (पाल् + अनीयर)।
(अ) पालनीयः
(ब) पालनीया
(स) पालनीयम्
(द) न कोऽपि
उत्तरम् :
(स) पालनीयम्

11. मानवः ……………. (समाज + ठक्) प्राणी अस्ति।
(अ) सामाजिकः
(ब) सामाजिकी
(स) सामाजिकम्
(द) न कोऽपि
उत्तरम् :
(अ) सामाजिकः

12. ……………. (लौकिक + ङीप्) उन्नतिः यश: वर्धयति।
(अ) लौकिकः
(ब) लौकिकी
(स) लौकिकम्
(द) न कोऽपि
उत्तरम् :
(ब) लौकिकी

13. (शिष्य + टाप) ……………. जलेन लताः सिञ्चति।
(अ) शिष्या
(ब) शिष्ये
(स) शिष्या
(द) न कोऽपि
उत्तरम् :
(स) शिष्या

14. गुरोः (गुरु + त्व) वर्णयितुं न शक्यते।
(अ) गुरुत्वम्
(ब) गुरुत्वः
(स) गुरुत्वम्
(द) न कोऽपि
उत्तरम् :
(अ) गुरुत्वम्

15. मा भव …………….. (मान + णिनि)।
(अ) मानी
(ब) मानिनौ
(स) मानिनः
(द) न कोऽपि
उत्तरम् :
(अ) मानी

16. (उदार + तल्) ……………. गुणः न सुलभः।
(अ) उदारतम्
(ब) उदारता
(स) उदारतः
(द) न कोऽपि
उत्तरम् :
(ब) उदारता

17. ……………. (राजन् + ङीप) प्रासादं गच्छति।
(अ) राजनी
(ब) राजिनी
(स) राज्ञी
(द) न कोऽपि
उत्तरम् :
(स) राज्ञी

18. गता रेल …………… (गन्तु + ङीप्)।
(अ) गन्त्री
(ब) गन्त्री
(स) गन्त्र्यः
(द) न कोऽपि
उत्तरम् :
(ब) गन्त्री

19. एकं …………… (सप्ताह + ठक्) पत्रम् आनय।।
(अ) साप्ताहिकः
(ब) साप्ताहिकी
(स) साप्ताहिकम्
(द) न कोऽपि
उत्तरम् :
(स) साप्ताहिकम्।

20. …………… (योग + इनि) ईश्वरं भजन्ते।
(अ) योगी
(ब) योगिनो
(स) योगिनः
(द) न कोऽपि
उत्तरम् :
(स) योगिनः।

प्रश्न 2.
रिक्तस्थानानि यथानिर्दिष्ट पदेन पूरयत – (रिक्त-स्थानों की पूर्ति निर्देशानुसार कीजिए-)
(क) रूपं यथा ………….” महार्णवस्य। (शम् + क्त)
(ख) ” ” नृत्यन्ति। (शिखा + इनि)
(ग) सलिलतीरं ……………. पक्षिण: वायसगणाः च। (वस् + णिनि)
(घ) अपयानक्रमो नास्ति …………”” अप्यन्यत्र को भवेत्। (नी + तृच)
(ङ) तत्किमत्र प्राप्तकालं स्यादिति
समहात्मास्वकीय सत्यतपोबलमेव तेषां रक्षणोपायम् अमन्यत्। (वि + मृश् + शतृ)
(च) स्मरामि न प्राणिवधं यथाहं ………. कृच्छ्रे परमेऽपि कर्तुम्। (सम् + चिन्त् + ल्यप्)
(छ) अतः शील विशद्धौ ……..” …..” (प्र + यत् + तव्यत्)
(ज) …………” राज संसत्सु श्रुतवाक्या बहुश्रुता ! (वि + श्रु + क्त + टाप्)
(झ) स लोके लोके लभते कीर्तिं परत्र च शुभां (गम् + क्तिन्)
(ब) ततः प्रविशति दारकं ………” रदनिका। (ग्रह + क्तवा)
(ट) उष्णं हि ………….. स्वदते। (भुज् + कर्म + शानच)
(ठ) कालोऽपि नो ……………” यमो वा। (नश् + णिच् + तुमुन्)
(ड) अस्ति कालिन्दीतीरे …… पुरं नाम नगरम् (योग + इनि + ङीप)
(ढ) हम्मीरदेवेन साकं युद्धं ……… “। (कृ + क्तवतु)
(ण) सः पराक्रमं …”दुर्गान्निः सृत्य सङ्ग्रामभूमौ निपपात्। (कृ + शानच्)
उत्तराणि –
(क) शान्तम्
(ख) शिखिनः
(ग) वासिनः
(घ) नेता
(ङ) विमृशन्
(च) सञ्चिन्त्य
(ज) विश्रुता
(झ) गीतम्
(ञ) गृहीत्वा
(ट) भुज्यमान
(ठ) नाशायतुम्
(ड) यागिना
(ढ) कृतवान्
(ण) कुर्वाणः।

प्रश्न 3.
रिक्तस्थानं प्रकोष्ठात् पदं चित्वा लिखत – (रिक्तस्थान को कोष्ठक से पद चुनकर भरो-)
(क) इति दारकमादाय …………….. रदनिका। (निष्क्रान्तः/निष्क्रान्ता)
(ख) मम हृदये नित्य …………….. स्तः। (सन्निहितो/सन्निहितः)
(ग) किन्तु अनुज्ञां गन्तु शक्येत्। .. (प्राप्त्वा/प्राप्य)
(घ) वार्तालापं …………….. भृत्यौ रत्ना च बहिरायान्ति। (श्रुतौ/श्रुत्वा)
(ङ) दारकस्य कर्णमेव ……………” प्रवृत्तोऽसि। (भङ्क्तुम्/भञ्जयितुम्)
(च) ……………..” अस्मि तव न्यायालये। (पराजित:/पराजितम्)
(छ) रामदत्तहरणौ …………….” आगच्छतः। (धावन्ता/धावन्तौ)
(ज) देवस्य शत्रु ………….” प्रभोर्मनोरथं साधयिष्यामः। . (हनित्वा/हत्वा)
(झ) रे रे “” …………. ! अहं यवनराजेन समं योत्स्यामि। (योद्धाः/योद्धार:!)
(ब) रक्ष स्व ………….. परहा भवार्यः। (जातिम्/जात्याः)
(ट) नशक्तो कालोपि नो ……………..। (नष्टुम्/नाशयितुम्)
(ठ) अतिविलम्बितं हि ………….. न तृप्तिमधिगच्छति। (भुञ्जन्/भुञ्जानो)
(ड) …………” चाग्निमौदर्यमुदीयति। (भुक्तम्/भुक्त:)
(ढ) स्वबाहुबलम् … योऽभ्युज्जीवति सः मानवः। (आश्रित्य/आश्रित्वा)
(ण) निर्जितं सिन्धुराजेन …………..” दीनचेतसम्। (शयमानम्/शयानम्)
उत्तराणि –
(क) निष्क्रान्ता
(ख) सन्निहितौ
(ग) प्राप्य
(घ) श्रुत्वा
(ङ) भञ्जयितुम्
(च) पराजितः
(छ) धावन्तौ
(ज) हत्वा
(झ) योद्धारः !
(ब) जातिम्
(ट) नाशयितुम्
(ठ) भुञ्जानो
(ड) भुक्तम्
(ढ) आश्रित्य
(ण) शयानम्।

प्रश्न 4.
प्रकृतिप्रत्ययं योजयित्वा पदरचनां कुरुत – (प्रकृति-प्रत्यय को जोड़कर पदरचना कीजिये।)
(क) (सम् + उद् + बह + शतृ) सलिलाऽतिभारं बलाकिनो वारिधराः नदन्तः।
(ख) शालिवनं (वि + पच् + क्त)
(ग) तान् मत्स्यान् (भक्ष् + तुमुन्) चिन्तयन्ति।
(घ) (मुह + क्त) मुखेन अति करुणं मन्त्रयसि।
(ङ) जीवितार्थं कुलं (त्यज् + क्तवा) यो जनोऽतिदूरं व्रजेत् किं तस्य जीवितेन ?
(च) तेन (रक्ष + अनीयर) रक्षा भविष्यन्ति।
(छ) भृत्यौ (हस् + शत) गृहाभ्यन्तरं पलायेते।
(ज) भो किं (कृ + क्तवतु) सिन्धु।
(झ) स्वपुस्तकालये (नि + सद् + क्त) दूरभाषयन्त्रं बहुषः प्रवर्तयति।
(ब) वत्स सोमधर ! मित्रगृहान्नैव (गम् + तव्यत्)
(ट) देवागारे (अपि + धा + क्त) द्वारे भजसे किम् ?
(ठ) ध्यानं (हा + क्त्वा) बहिरेहित्वम्।
(ड) शाकफल (वि + क्री + तृच्) दारकः कथं त्वामतिशेते।
(ढ) स लोके लभते (क + क्तिन्)
(ण) तद् ग्रहाण एतम् (अलम् + कृ + ण्वुल्)।
उत्तराणि :
(क) समुद्वहन्तः
(ख) विपक्वम्
(ग) भक्षितुम्
(घ) मुग्धेन
(ङ) त्यक्त्वा
(च) रक्षणीय
(छ) हसन्तौ
(ज) कृतवान्
(झ) निषण्णः
(ब) गन्तव्यम्
(ट) पिहित
(ठ) हित्वा
(ड) विक्रेतुः
(ढ) कीर्तिम
(ण) अलङ्कारकम्।।

प्रश्न 5.
कोष्ठकेषु प्रदत्तैः शब्दैः प्रकृति-प्रत्ययानुसारं रिक्तस्थानपूर्तिः करणीया। (कोष्ठकों में दिए गए शब्दों से प्रकृति-प्रत्यय के अनुसार रिक्त स्थान की पूर्ति कीजिए।)
1. (i) पाठः तु सदैव ध्यानेन एव ………………। (पठ् + अनीयर)
(ii) छात्रैः समये विद्यालयः ………………। (गम् + तव्यत्)
(iii) ……………. पुरुषः सफलतां लभते। (यत् + शानच्)
(iv) ……………. बालकः हसति। (गम् + शतृ)
(v) वाराणस्याम्……………. पुरुषाः निवसन्ति। (धर्म + ठक्)
उत्तराणि :
(i) पठनीयः
(ii) गन्तव्यः
(iii) यतमानः
(iv) गच्छन्
(v) धार्मिकाः।

2. (i) (विद्या + मतुप्) ……………… सर्वत्र सम्मान्यते।
(ii) पुत्रेण अनुशासनम् (पाल् + अनीयर) ……………।
(iii) सदा (सुख + इन्) …………… भव।
(iv) शस्त्रहीनः न (हन् + तव्यत्) ………………।
(v) जीवने (महत् + त्व) ……………… लभस्व।
उत्तराणि :
(i) विद्यावान्
(ii) पालनीयम्
(iii) सुखी
(iv) हन्तव्यः
(v) महत्त्वम्।

3. (i) बालिकाभिः राष्ट्रगीतं ……………… (गै + तव्यत्)।
(ii) छात्रैः ……………… (उपदेश) पालनीयाः।
(iii) ……………… (युष्मद्) शुद्धं जलं पातव्यम्।
(iv) मुनिभिः ……………… (तपस्) करणीयम्।
(v) न्यायाधीशेन न्यायः ……………..(कृ + अनीयर्)।
उत्तराणि :
(i) गातव्यम्
(ii) उपदेशाः
(iii) युष्माभिः
(iv) तपः
(v) करणीयः।

4. (i) ……………… (भवति) पाठः लेखनीयः।
(ii) विद्वद्भिः कविताः ……………… (रच् + अनीयर)।
(iii) अस्माभिः लताः ……………… आरोपयितव्याः।
(iv) पत्रवाहकेन पत्राणि ………………। (आ + नी + तव्यत्)
(v) ……………… (राजन्) प्रजाः पालनीयाः।
उत्तराणि :
(i) भवत्या
(ii) रचनीयाः
(iii) लताः
(iv) आरोपयितव्याः
(v) राज्ञा।

5. (i) त्वया सन्तुलित आहारः (कृ + तव्यत्) ………………
(ii) तव (कृश + तल्) ……………… मां भृशं तुदति।
(iii) विद्यायाः महत्त्वमपि ……………… (स्मृ + तव्यत्)।
(iv) सद्ग्रन्थाः सदैव ……………… (पठ् + अनीयर्)।
(v) अध्ययनेन मनुष्यः (गुण + मतुप्) ……………… भवति।
उत्तराणि :
(i) कर्त्तव्यः
(ii) कृशता
(iii) स्मर्तव्यम्
(iv) पठनीयाः
(v) गुणवान्।

6. (i) अस्याः ……………… (अनुज + टाप्) दीपिका अस्ति।
(ii) दीपिका क्रीडायाम् ……………… (कुशल + टाप्) अस्ति।।
(iii) प्रभादीपिकयो: माता ……………… (चिकित्सक + टाप्) अस्ति।
(iv) सा समाजस्य ……………… (सेवक + टाप्) अस्ति।
(v) सा तु स्वभावेन अतीव ……………… (सरल + आप्) अस्ति।
उत्तराणि :
(i) अनुजा
(ii) कुशला
(iii) चिकित्सिका
(iv) सेविका
(v) सरला।

7. (i) छात्रैः समये विद्यालयः (गम् + तव्यत्) ………………।
(ii) अद्य अस्माकं (वर्ष + ठक् + ङीप्) ……………… परीक्षा आरभते।
(iii) पर्यावरणस्य (महत् + त्व) ……………… सर्वे जानन्ति।
(iv) (बुद्धि + मतुप्) ……………… नरः सर्वत्र मानं लभते।
(v) जनकं (सेव् + शानच्) ……………… पुत्रः प्रसन्नः अस्ति।
उत्तराणि :
(i) गन्तव्यः
(ii) वार्षिकी
(iii) महत्त्वम्
(iv) बुद्धिमान्
(v) सेवमानः।

8. (i) मम ……………… (कीदृश + ङीप्) इयं क्लेशपरम्परा।
(ii) मारयितुम् ……………. (इष् + शतृ) स कलशं गृहाभ्यन्तरे क्षिप्तवान्।
(iii) छलेन अधिगृह्य ……………… (क्रूर + तल्) भक्षयसि।
(iv) अधुना ……………… (रमणीय + टाप्) हि सृष्टिरेव।
(v) अनेकानि अन्यानि ……………… (दृश् + अनीयर) स्थलानि अपि सन्त।
उत्तराणि :
(i) कीदृशी
(ii) इच्छन्
(iii) क्रूरतया
(iv) रमणीया
(v) रमणीयता।

9. (i) नृपेण प्रजा (पाल् + अनीयर) ………………।
(ii) आचार्यस्य (गुरु + त्व) ……………… वर्णयितुं न शक्यते।
(iii) पुरस्कार (लभ् + शानच्) ……………… छात्रः प्रसन्नः भवति।
(iv) मनुष्यः (समाज + ठक्) ……………… प्राणी अस्ति।
(v) प्रकृते (रमणीय + तल) ……………… दर्शनीया अस्ति।
उत्तराणि :
(i) पालनीया
(ii) गुरुत्वम्
(iii) लभमानः
(iv) सामाजिकः
(v) रमणीयता।

प्रश्न 6.
कोष्ठके दत्तान् प्रकृतिप्रत्ययान् योजयित्वा अनुच्छेदं पुनः उत्तर-पुस्तिकायां लिखत –
(कोष्ठक में दिए हुए प्रकृति-प्रत्ययों को जोड़कर अनुच्छेद को पुनः उत्तर-पुस्तिका में लिखिए)
1. पर्यावरणस्य (महत् + त्व) (i) ……………… कः न जानाति ? परं निरन्तरं (वृध् + शानच्) (ii) ……….. प्रदूषणेन मानव जातिः विविधैः रोगैः आक्रान्ता अस्ति। अस्माभिः (ज्ञा + तव्यत्) (iii) …………… यत् पर्यावरणस्व रक्षणे एव अस्माकं रक्षणम्। एतदर्थम् (जन + तल) (iv) …………… जागरूका कर्तव्या। स्थाने स्थाने वृक्षारोपणम् अवश्यम् (कृ + अनीयर) (v) ……………। यतो हि वृक्षाः पर्यावरणरक्षणे अस्माकं सहायकाः सन्ति।
उत्तरम् :
पर्यावरणस्य महत्त्वं कः न जानाति ? परं निरन्तरं वर्धमानेन प्रदूषणेन मानवजातिः विविधैः रोगैः आक्रान्ना अस्ति। अस्माभिः ज्ञातव्यम् यत् पर्यावरणस्य रक्षणे एव अस्माकं रक्षणम्। एतदर्थम् जनता जागरूका कर्त्तव्याः। स्थान-स्थाने वृक्षारोपणम् अवश्यम् करणीयम्। यतो हि वृक्षाः पर्यावरणरक्षणे अस्माकं सहायकाः सन्ति।

2. ओदनं पचन्ती (i) ……………… (पुत्र + ङीप) कथितवती – किं त्वं जानासि कालस्य (ii) ……….. (महत् + त्व) ? काल: तु सततं चक्रवत् (ii) ……………… (परिवृत् + शानच्) वर्तते। ये जनाः अस्य अस्थिरता अनुभूय स्वकार्याणि यथासमयं कुर्वन्ति, ते एव (iv) ……………… (बुद्धि + मतुप)। ते जनाः (v) ……. (बन्द अनीयर्) भवन्ति।
उत्तरम् :
ओदनं पचन्ती पुत्री कथितवती-किं त्वं जानासि कालस्य महत्त्वम् ? कालः तु सततं चक्रवत् परिवर्तमान वर्तते। ये जनाः अस्य अस्थिरताम् अनुभूय स्वकार्याणि यथासमयं कुर्वन्ति, ते एव बुद्धिमन्तः। ते जनाः वन्दनीया: भाः

3. जानासि अस्माकं विद्यार्थिनां कानि (कृ + तव्यत्) (i) ……………… ? अस्माभिः विद्यालयस्य अनुशासनं (पान + अनीयर) (ii) ………………। सर्वैः सहपाठिभिः सह (मित्र + तल) (iii) ……………… आचरणीया। छात्रजीवने परिश्रमस्य (महत् + तल्) (iv) ……………… वर्तते। सत्यम् एव उक्तम् (सुखार्थ + इन्) (v) ……………… कुतो विद्या?
उत्तरम् :
जानासि अस्माकं विद्यार्थिनां कानि कर्त्तव्यानि ? अस्माभिः विद्यालयस्य अनुशासनं पालनीयम्। सबै सहपाठिभिः सह मित्रता आचरणीया। छात्रजीवने परिश्रमस्य महत्ता वर्तते। सत्यम् एव उक्तम् – सुखार्थिनः मन विद्या ?

4. कार्यं तु सदैव ध्यानेन एव (i) ……………… (कृ + अनीयर)। (ii)……………… (फल + इन्) वृक्षाः एन सदैव नमन्ति। शिक्षायाः (iii) ……………… (महत् + त्व) तु अद्वितीयम् एव। (iv)……………… (वृध् + शानच बालाः नृत्यन्ति। (v) ……………… (अज + टाप्) शनैः शनैः चलति।
उत्तरम् :
कार्यं तु सदैव ध्यानेन एव करणीयम्। फलिनः वृक्षाः एव सदैव नमन्ति। शिक्षायाः महत्त्वं तु अद्वितीयम् एव। वर्धमानाः बालाः नृत्यन्ति। अजा शनैः शनैः चलति।।

5. एकदा पितरं (सेव् + शानच्) (i) ……………… पुत्रः तम् अपृच्छत् – ‘हे पितः! संसारे कः पूज्यते ? ‘ पिता अवदत् – (गुण + मतुप्) (ii) ……………… सर्वत्र पूज्यते। यः सेवायाः (महत् + त्व) (iii) ……………… सम्यक् जानाति, सः समाजे सदा (वन्द् + अनीयर्) (iv) ……………… भवति। अतः सर्वैः (मानव + तल्) (v) ………… सेवितव्या।’
उत्तरम् :
एकदा पितरं सेवमानः पुत्रः तम् अपृच्छत् – ‘हे पितः, संसारे कः पूज्यते ?’ पिता अवदत् – ‘ गुणवान् सर्वत्र पूज्यते। यः सेवायाः महत्त्वं सम्यक् जानाति, सः समाजे सदा वन्दनीयः भवति। अतः सर्वैः मानवता सेवितव्या।’

6. त्वं (गुण + मतुप्) (i) ……………… असि। तव प्रकृतिः (शोभन + टाप) (ii) ……………… अस्ति। अतः (विनय + इन्) (iii) ……………… अपि भव। सदैव (समाज + ठक्) (iv) ……………… कार्यमपि (कृ + शतृ) (v) ……………… त्वं लोके यशः प्राप्स्यसि।
उत्तरम् :
त्वं गुणवान् असि। तव प्रकृतिः शोभना अस्ति। अतः विनयी अपि भव। सदैव सामाजिक कार्यमपि कुर्वन् त्वं लोके यशः प्राप्स्यसि।

7. छात्रैः यथाकालम् एव विद्यालयस्य कार्यः (i) …………………. (कृ + तव्यत्)। ये छात्राः अध्ययनस्य (ii) ……………… (महत् + त्व) न जानन्ति तेषां कृते (iii) ……………… (सफल + तल) सन्दिग्धा भवति, परञ्च ये छात्रा: आलस्यं विहाय अहर्निशं परिश्रमं कुर्वन्ति तेषां कृते (iv) ……………… (वर्ष + ठक् + ङीप्) परीक्षा भयं न जनयति। (v) ……………… (बुद्धि + मतुप्) छात्राः पुरुषार्थे विश्वसन्ति न तु केवलं भाग्ये। अतः सर्वैः स्वकार्याणि समये (vi) ……………… (कृ + अनीयर)।
उत्तरम् :
छात्रैः यथाकालम् एव विद्यालयस्य कार्यः कर्त्तव्यम्। ये छात्राः अध्ययनस्य महत्त्वं न जानन्ति तेषां कृते सफलता सन्दिग्धा भवति, परञ्च ये छात्रा: आलस्यं विहाय अहर्निशं परिश्रमं कुर्वन्ति तेषां कृते वार्षिकी परीक्षा भयं न जनयति। बुद्धिमन्तः छात्राः पुरुषार्थे विश्वसन्ति न तु केवलं भाग्ये। अतः सर्वैः स्वकार्याणि समये करणीयानि।।

8. पिता पुत्रम् उपादिशत् यत् त्वया कुमार्गः (i) ……………… (त्यज् + तव्यत्) (ii) ……………… (प्र + यत् + शानच्) जनाः साफल्यं प्राप्नुवन्ति। यः नरः सत्यवादी (iii) ……………… (निष्ठा + मतुप्) च सः एव श्रेष्ठः। वृक्षारोपणम् अस्माकं (iv) ……………… (नीति + ठक्) कर्त्तव्यम्। मातृभूमिः सदैव (v)……………… (वन्दनीय + टाप्) भवति।
उत्तरम् :
पिता पुत्रम् उपादिशत् यत् त्वया कुमार्गः त्यक्तव्यः प्रयतमानाः जनाः साफल्यं प्राप्नुवन्ति। यः नरः सत्यवादी निष्ठावान् च सः एव श्रेष्ठः। वृक्षारोपणम् अस्माकं नैतिकं कर्त्तव्यम्। मातृभूमिः सदैव वन्दनीया भवति।

9. एक: कैयट: नाम विद्वान् आसीत्। सः प्रातः (i) ……………… (काल + इ) शास्त्राणाम् अध्ययने रतः भवति स्म। एकदा राजा तं (ii) ……………… (बुद्धि + मतुप्) द्रष्टुं तस्य कुटीरं (iii) ……………… (गम् + तव्यत्) इति निश्चितवान्। तत्र गत्वा तस्य (iv) ……………… (दरिद्र + तल्) दूरीकर्तुं सः तस्मै स्वर्णमुद्राः अयच्छत्। कैयटः अवदत्- “धनस्य (v) ……………… (लोभ + इन्) जनाः आसक्ताः भूत्वा दुःखिनः भवन्ति। अतः मम आनन्दं मा नाशयतु इति।”
उत्तरम् :
एक: कैयटः नाम विद्वान् आसीत्। सः प्रात:काले शास्त्राणाम् अध्ययने रतः भवति स्म। एकदा राजा तं बुद्धिमन्तं द्रष्टुं तस्य कुटीरं गन्तव्यम् इति निश्चितवान्। तत्र गत्वा तस्य दरिद्रतां दूरीका सः तस्मै स्वर्णमुद्राः अयच्छत्। कैयटः अवदत् – “धनस्य लोभिनः जनाः आसक्ताः भूत्वा दुःखिनः भवन्ति। अतः मम आनन्दं मा नाशयतु इति।”
धानस्य शोभा खलु (i)……………… (दृश् + अनीयर)। शीघ्र-शीघ्रं (ii) ……………… (चल + शतृ) जनाः प्रसन्नाः भवन्ति। ते वायोः (iii) ……………… (शीतल + तल) अनुभवन्ति। (iv) ……………… (पक्ष + इन्) मधुर स्वरेण गायन्ति। बालकाः (v) ……………… (बालक + टाप्) च कन्दुकेन क्रीडन्ति।
उत्तरम् :
प्रात:काले उद्यानस्य शोभा खलु दर्शनीया। शीघ्रं-शीघ्रं चलन्तः जनाः प्रसन्नाः भवन्ति। ते वायोः शीतलताम् अनुभवन्ति। पक्षिणः मधुरस्वरेण गायन्ति। बालकाः बालिकाः च कन्दुकेन क्रीडन्ति।।

11. जीवने शिक्षायाः सर्वाधिकं (i) ……………… (महत् + त्व) वर्तते। बालः भवेत् (ii) ……………… (बालक + टाप्) वा भवेत्, ज्ञान प्राप्तुं सर्वैः एव प्रयत्नः (iii) ……………… (कृ + तव्यत्)। शिक्षिताः (iv) …….. (प्राण + इन्) परोपकारं (v) ………. …. (कृ + शानच) देशस्य सर्वदा हितमेव चिन्तयन्ति।
उत्तरम् :
जीवने शिक्षायाः सर्वाधिक महत्त्वं वर्तते। बालः भवेत् बालिका वा भवेत्, ज्ञानं प्राप्तुं सर्वैः एव प्रयत्नः कर्तव्यः। शिक्षिताः प्राणिनः परोपकारं कुर्वाणा: देशस्य सर्वदा हितमेव चिन्तयन्ति।

प्रश्न 7.
निम्नलिखित पदों में प्रकृति-प्रत्यय को अलग कीजिए –
अधीतः, जग्धवान्, गृहीत्वा, उपगम्य, पातुम्।।
उत्तरम् :
अधि + इ + क्त; अद् + क्तवतु ग्रह + क्त्वा, उपगम् + ल्यप्, पा + तुमुन्।

प्रश्न 8.
निम्नलिखित में प्रकृति-प्रत्यय का मेल कीजिए –
कर्ता + ङीप, एडक + टाप, भाग् + इनि, बहु + तमप, निम्न + तरप्, रक्ष् + तव्यत्, युध् + शानच्, वस् + शतृ, स्तु + क्तवतु।
उत्तरम् :
की, एडका, भागी, बहुतमः, निम्नतरः, रक्षितव्यः, युध्यमानः, वसन् स्तुतवान्।

प्रश्न 9.
निम्नलिखित प्रत्ययान्त शब्दों को ‘कृत्”तद्धित’ और ‘स्त्री’ प्रत्ययान्त के रूप में अलग-अलग छाँटिये कोकिला, हन्त्री, शूद्रता, पीत्वा, नीति, भूता, पूजनम्, हन्तव्यः, लेखनीयः, भगवती, लघुता, शिशुत्वम्।
उत्तरम् :
कृत्-पीत्वा, नीति, पूजनम्, हन्तव्यः, लेखनीयः। तद्धित्-शूद्रता, लघुता, शिशुत्वम्। स्त्री-कोकिला, हन्त्री, भूता, भगवती।

प्रश्न 10.
प्रत्येक धातु में कोई पाँच प्रत्यय जोड़कर उनका एक-एक उदाहरण लिखिए –
पठ्, नम्, पच्, दा, लभ्, दृश्, गम्, हस्, इष्, लभ्।
उत्तरम् :

प्रश्न 11.
अधोलिखितवाक्येषु रेखांकितपदानां प्रकृति-प्रत्यय-विभाग प्रत्ययान्तपदं वा लिखत –
(निम्नलिखित वाक्यों में रेखांकित पदों में प्रकृति-प्रत्यय अलग कीजिये अथवा प्रत्ययान्त शब्द लिखिए-)
(1) अहं शयनं परित्यज्य भ्रमणं गच्छामि।
(2) श्यामः पुस्तकं क्रेतुं गमिष्यति।
(3) मया रामायणं श्रुतम्।
(4) फलं खादन् बालकः हसति।
(5) सुरेशः ग्रामं गत्वा धावति।
(6) सर्वान् विचिन्त्य ब्रू (वच्) + तव्यत्।
(7) मुकेशः भोजनं खाद + शत पुस्तकं पठति।
(8) स: गृहकार्यं कृ + क्त्वा क्रीडति।
(9) सीता ग्रामात् आ + गम् + ल्यप् नृत्यति।
(10) भारत: पठ्+तुमुन् इच्छति।
उत्तर :
(1) परि + त्यज् + ल्यप्,
(2) क्री + तुमुन्,
(3) श्रु+ क्त,
(4) खाद् + शत,
(5) गम् + क्त्वा,
(6) वक्तव्यम्,
(7) खादन्,
(8) कृत्वा,
(9) आगत्य,
(10) पठितुम्।।

प्रश्न 12.
निर्देशम् अनुसृज्य उदाहरणानुसारं संयोज्य वाक्यसंयोजनं क्रियताम्।
(निर्देश का अनुसरण करके उदाहरणानुसार जोड़कर वाक्यों को जोड़िए।)
(क) पूर्ववाक्ये ‘क्त्वा’ प्रत्ययं प्रयुज्य वाक्यं संयोजयत
(पहले वाक्य में ‘क्त्वा’ प्रत्यय का प्रयोग कर वाक्य-संयोजन कीजिए) महेशः खेलति। महेशः धावति।
उत्तरम् :
महेशः खेलित्वा धावति।

(ख) ‘तुमुन्’ प्रत्ययप्रयोगं कृत्वा वाक्यसंयोजनं क्रियताम्-(तुमुन् प्रत्यय का प्रयोग कर वाक्य-संयोजन कीजिए –
रामः वनं गच्छति। रामः अश्वम् आरोहति।
उत्तरम् :
रामः वनं गन्तुम् अश्वम् आरोहति।

(ग) पूर्ववाक्ये शतृप्रत्ययं प्रयुज्य वाक्यं पुनः लिखत –
(पूर्व वाक्य में ‘शतृ’ प्रत्यय का प्रयोग कर वाक्य को पुनः लिखिए-)
छात्राः श्यामपट्ट स्पृशति। छात्राः गृहं गच्छति।
उत्तरम् :
छात्राः श्यामपट्ट स्पृशन्तः गृहं गच्छन्ति।

(घ) ‘तुमुन्’ प्रत्ययं प्रयुज्य वाक्यं पुनः लिखत –
(तुमुन् प्रत्यय का प्रयोग कर वाक्य को पुनः लिखिए-)
त्वं जलं पिबसि। त्वं कूपं गच्छसि।
उत्तरम् :
त्वं जलं पातुं कूपं गच्छसि।

प्रश्न 13.
स्थूलपदानाम् ‘प्रकृतिप्रत्ययः’ पृथक् संयोगं कृत्वा उत्तर-पुस्तिकायां लिखत –
(मोटे शब्दों के प्रकृति-प्रत्यय अलग करके उत्तर-पुस्तिका में लिखिए)
1. (i) अद्य मानवः सेवाया महत्त्वं न जानाति। (आज मनुष्य सेवा का महत्त्व नहीं जानता है।)
(ii) समाजसेवा करणीया। (समाज सेवा की जानी चाहिए।)
(iii) बालकोऽयं गुणवान् अस्ति। (यह बालक गुणवान् है।)
(iv) लोभी न भवेत्। (लोभी नहीं होना चाहिए।)
(v) सा बुद्धिमती अचिन्तयत्। (वह बुद्धिमती सोचने लगी।)
उत्तराणि :
(i) महत् + त्व
(ii) कृ + अनीयर् + टाप्
(iii) गुण + मतुप् (वत्)
(iv) लोभ + इनि
(v) बुद्धि + मतुप् + ङीप।

2. (i) गुरुः वन्दनीयः। (गुरु वन्दना के योग्य होता है।)
(ii) ज्ञानवान् एव गुरुत्वं प्राप्नोति। (ज्ञानवान् ही गुरुत्व को प्राप्त करता है।)
(iii) देशे अनेकानि दर्शनीयानि स्थानानि सन्ति। (देश में अनेक दर्शनीय स्थान हैं।)
(iv) गुणी एव सर्वत्र पूज्यः। (गुणी ही सब जगह पूज्य होता है।)
(v) शिक्षिका गणितं पाठयति। (शिक्षिका गणित पढ़ाती है।)
उत्तराणि :
(i) वन्द् + अनीयर्
(ii) गुरु + त्व
(iii) दृश् + अनीयर्
(iv) गुण + इन्
(v) शिक्षक + टाप्।

3. (i) पुस्तकानां महत्तां कः न जानाति ? (पुस्तकों की महत्ता को कौन नहीं जानता ?)
(ii) गायिका मधुरं गायति। (गायिका मधुर गाती है।)।
(iii) कार्यं कुर्वाणाः छात्राः अङ्कान् लभन्ते। (कार्य करते हुए छात्र अंक प्राप्त करते हैं।)
(iv) बालकैः गुरवः नन्तव्याः। (बालकों द्वारा गुरु को नमस्कार किया जाना चाहिए।)
(v) अश्वा धावति। (घोड़ी दौड़ती है।)
उत्तराणि :
(i) महत् + तल्
(ii) गायक + टाप्
(iii) कृ + शानच्
(iv) नम् + तव्यत्
(v) अश्व + टाप।

4. (i) सः वेत्रासने आसीनः। (वह कुर्सी पर बैठा है।)
(ii) राज्ञी राजानम् अपृच्छत्। (रानी ने राजा से पूछा।)
(iii) इन्द्राणी इन्द्रं पृच्छति। (इन्द्राणी इन्द्र से पूछती है।)
(iv) मन्त्रिणः संसदि भाषन्ते। (मन्त्री संसद में बोलते हैं।)
(v) अजाः क्षेत्रे चरन्ति। (बकरियाँ खेत में चरती हैं।)
उत्तराणि :
(i) आस् + शानच्
(ii) राजन् + ङीप्
(iii) इन्द्र + ङीप्
(iv) मन्त्र + इन्
(v) अज + टाप्।

5. (i) मासिकं पत्रम् आनय। (मासिक पत्र लाइए।)
(ii) सुखार्थिनः कुतो विद्या। (सुख चाहने वाले को विद्या कहाँ ?)
(iii) वाष्पयानमाला संधावति वितरन्ती ध्वानम्।(रेलगाड़ी शोर बाँटती हुई दौड़ रही है।)
(iv) जगति शुद्धिकरणं करणीयम्। (संसार में शुद्धिकरण करना चाहिए।)
(v) ललितलतानां माला रमणीया। (सुन्दर लताओं की माला रमणीय है।)
उत्तराणि :
(i) मास + ठक्
(ii) सुख + अर्थ + इन्
(iii) वितरत् + ङीप्
(iv) कृ + अनीयर्
(v) रमू + अनीयर् + टाप्।

6. (i) लक्षणवती कन्यां विलोक्य सः पृच्छति (लक्षणवाली कन्या को देखकर वह पूछता है।)
(ii) अन्योऽपि बुद्धिमान् लोके मुच्यते महतो भयात्।। (और भी बुद्धिमान् लोक के महान् भय से मुक्त हो जाते हैं।)
(iii) शृगालः हसन् आह। (शृगाल ने हँसते हुए कहा।)
(iv) मया सा चपेटया प्रहरन्ती दृष्टा। (मैंने उसे थप्पड़ से प्रहार करती हुई देखा है।)
(v) तर्हि त्वया अहं हन्तव्यः। (तो तुम मुझे मार देना।)
उत्तराणि :
(i) लक्षणवत् + ङीप्
(ii) बुद्धि + मतुप्
(iii) हस् + शतृ
(iv) प्रहरत् + ङीप
(v) हन् + तव्यत्।

7. (i) शुनी सर्वम् इन्द्राय निवेदयति। (कुतिया सब कुछ इन्द्र से निवेदन कर देती है।)
(ii) आचार्य सेवमानः शिष्यः विद्यां लभते। (आचार्य की सेवा करता हुआ शिष्य विद्या प्राप्त करता है।)
(iii) श्रद्धावान् लभते ज्ञानम्।। (श्रद्धावान् ज्ञान प्राप्त करता है।)
(iv) अद्य अस्माकं वार्षिकी परीक्षा आरभते। (आज हमारी वार्षिक परीक्षा आरम्भ है।)
(v) सः कार्यं कुर्वन् पठति अपि। (वह कार्य करता हुआ भी पढ़ता है।)
उत्तराणि :
(i) श्वन् + ङीप्
(ii) सेव + शानच्
(iii) श्रद्धा + मतुप् (वत्)
(iv) वर्ष + ठक् + ङीप्।
(v) कृ + शतृ।

8. (i) जीवने विद्यायाः अपि महत्त्वं वर्तते। (जीवन में विद्या का भी महत्त्व है।)
(ii) तर्हि त्वया सद्ग्रन्थाः अपि पठनीयाः। (तो तुम्हें सद्ग्रन्थ भी पढ़ने चाहिए।)
(iii) पठनेन नरः गुणवान् भवति। (पढ़ने से मनुष्य गुणवान् होता है।)
(iv) किं त्वं जानासि कालस्य महत्त्वम् ? (क्या तुम समय का महत्त्व जानते हो ?)
(v) कालः तु सततम् चक्रवत् परिवर्तमानः वर्तते। (समय तो निरन्तर चक्र की तरह बदलता रहता है।)
उत्तराणि :
(i) महत् + त्व
(ii) पत् + अनीयर्
(iii) गुण + मतुप् (वत्)
(iv) महत् + त्व
(v) परिवृत् + शानच्।

9. (i) ये जनाः अस्थिरताम् अनुभूय स्वकार्याणि यथासमयं कुर्वन्ति ते एव बुद्धिमन्तः।
(जो लोग अस्थिरता का अनुभव करके अपने कार्य समय पर करते हैं, वे ही बुद्धिमान् हैं।)
(ii) ते जनाः वन्दनीयाः भवन्ति। (वे लोग वन्दना करने योग्य होते हैं।)
(iii) जनाः तीव्र धावन्तः गच्छन्ति। (लोग तीव्र दौड़ते हुए जाते हैं।)
(iv) गृहं गच्छन्त्यः छात्राः प्रसीदन्ति। (घर जाती हुई छात्राएँ प्रसन्न होती हैं।)
(v) कालः परिवर्तमानः वर्तते। (समय बदलता रहता है।)
उत्तराणि :
(i) अस्थिर + तल, बुद्धि + मतुप्
(ii) वन्द् + अनीयर् + टाप्
(iii) धाव् + शतृ
(iv) गच्छत् + ङीप्
(v) परिवृत् + शानच्।

10. (i) कार्यं तु सदैव ध्यानेन एव करणीयम्। (कार्य सदैव ध्यान से ही करना चाहिए।)
(ii) फलिनः वृक्षाः एव सदैव नमन्ति। (फल वाले वृक्ष ही सदा झुकते हैं।)
(iii) शिक्षायाः महत्त्वं तु अद्वितीयम् एव। (शिक्षा का महत्त्व तो अद्वितीय है।)
(iv) वर्धमानाः बालाः नृत्यन्ति। (बढ़ती हुई बालाएँ नाचती हैं।)
(v) अजाः शनैः शनैः चलति।
(बकरी धीरे-धीरे चलती है।)
उत्तराणि :
(i) कृ + अनीयर्
(ii) फल + इन्
(iii) महत् + त्व
(iv) वृध् + शानच्
(v) अज + टाप्।

11. (i) कार्यं सदैव शीघ्रं परन्तु धैर्येण कर्त्तव्यम्। (कार्य सदैव शीघ्र परन्तु धैर्यपूर्वक करना चाहिए।)
(ii) वर्धमाना बालिका शीघ्रं शीघ्रं धावति। (बढ़ती बालिका जल्दी-जल्दी दौड़ती है। )
(iii) गुणिनः जनाः सदा वन्दनीयाः। (गुणी लोग सदैव वन्दना करने योग्य हैं।)
(iv) वृक्षाणां महत्त्वं कः न जानाति ? (वृक्षों का महत्त्व कौन नहीं जानता ?)
(v) कोकिला मधुर स्वरेण गायति। (कोयल मधुर स्वर से गाती है।)
उत्तराणि :
(i) कृ + तव्यत्
(ii) वृध् + शानच् + ङीप
(iii) गुण + इन्
(iv) महत् + त्व
(v) कोकिल + टाप।

12. (i) पुस्तकानाम् अध्ययनं करणीयम्। (पुस्तकों का अध्ययन करना चाहिए।)
(ii) मन्त्रिणः सदसि भाषन्ते। (मन्त्री सभा में भाषण करते हैं।)
(iii) वर्तमाना शिक्षापद्धतिः सुकरा। (वर्तमान शिक्षा पद्धति सरल है।)
(iv) त्वं स्व अज्ञानतां मा दर्शय। (तुम अपनी अज्ञानता को मत दिखाओ।)
(v) नर्तकी शोभनं नृत्यति। (नर्तकी सुन्दर नाचती है।)
उत्तराणि :
(i) कृ + अनीयर्
(ii) मन्त्र + इन्
(iii) वृत् + शानच् + टाप्
(iv) अज्ञान + तल्
(v) नर्तक+ङीप्।

13. (i) अस्माभिः सेवकाः पोषणीयाः। (हमें सेवकों का पोषण करना चाहिए।)
(ii) पक्षिणः वृक्षेषु तिष्ठन्ति। (पक्षी वृक्ष पर बैठते हैं।)
(iii) पृथिव्याः गुरुत्वं सर्वे जानन्ति। (पृथ्वी की गुरुता को सभी जानते हैं।)
(iv) सेवमाना: सेवकाः धनं लभन्ते। (सेवा करते हुए सेवक धन पाते हैं।)
(v) अश्वा वरं धारयति। (घोड़ी वर को धारण करती है।)
उत्तराणि :
(i) पुष् + अनीयर्
(ii) पक्ष + इन्
(iii) गुरु + त्व
(iv) सेव् + शानच्।
(v) अश्व + टाप्।

14. (i) बालकैः गुरवः नन्तव्याः।
(बालकों को गुरुजनों का नमन करना चाहिए।)
(ii) कार्यं कुर्वाणा: छात्राः अङ्कान् लभन्ते। (कार्य करते छत्र अंक प्राप्त करते हैं।)
(iii) भाग्यशालिनः जनाः विश्रामं कुर्वन्ति। (भाग्यशाली लोग आराम करते हैं।)
(iv) गायिका मधुरं गायति। (गायिका मधुर गाती है।)
(v) पुस्तकानां महत्तां कः न जानाति। (पुस्तकों की महत्ता कौन नहीं जानता।)
उत्तराणि :
(i) नम् + तव्यत्
(ii) कृ + शानच्
(iii) भाग्यशाल + इन्
(iv) गायक + टाप्।
(v) महत् + तल्।

प्रश्न 14.
प्रकृतिप्रत्ययं योजयित्वा पदरचनां कुरुत।
(प्रकृति प्रत्यय को मिलाकर पदरचना कीजिये।)
(क) जन् + क्त
(ख) क्रीड् + शतृ
(ग) त्यज् + क्तवा
(घ) वि + श्रम् + ल्यप्
(ङ) भक्ष् + तुमुन्
(च) नि + वृत् + क्तिन्
(छ) प्र + यत् + तव्यत्
(ज) भुज् + शानच
(झ) गुह् + क्त + टाप्
(ब) जि + अच्
(ट) ग्रह् + ण्वुल्
(ठ) लभ् + क्तवतु
(ड) अधि + वच् + तृच्
(द) कृ + क्तवतु + ङीप्
(ण) कृ + अनीयर्
उत्तरम् :
(क) जातः
(ख) क्रीडन्
(ग) त्यक्तवा
(घ) विश्रम्य
(ङ) भक्षितुम्
(च) निवृत्तिः
(छ) प्रयतितव्यम्
(ज) भुञ्जानः
(झ) गूढ
(ब) जयः
(ट) ग्राहकः
(ठ) लब्धवान्
(ड) अधिवक्ता
(ढ) कृतती
(ण) करणीयः।

प्रश्न 15.
अधोलिखित पदेषु प्रकृतिप्रत्यय विभागः क्रियताम्।
(निम्नलिखित पदों में प्रकृति-प्रत्यय पृथक् कीजिये)
(क) प्रयुक्तम्
(ख) भवितव्यम्
(ग) गन्तुम्
(घ) पर्यटन्तः
(ङ) वहमानस्य
(च) क्रीत्वा
(छ) दृष्टिः
(ज) कर्ता
(झ) अतितराम्
(ब) प्रतीक्षमाणः
(ट) करणीया
(ठ) प्रत्यभिज्ञाय
(ड) कारकः
(ढ) कृतवती
(ण) विक्रेता।
उत्तरम् :
(क) प्रयुक्तम् = प्र + युज् + क्त
(ख) भवितव्यम् = भू + तव्यत्
(ग) गन्तुम् = गम् + तुमुन्
(घ) पर्यटन्तः = परि + अट् + शत् (प्र.ब.व.)
(ङ) वहमानस्य = वह् + शानच् (ब.ए.व.)
(च) क्रीत्वा = क्री + क्तवा
(छ) दृष्टिः = दृश् + क्तिन्
(ज) कर्ता = कृ + तृच्
(झ) अतितराम् = अति + तरप् + टाप् (द्वि.ए.व.)
(ब) प्रतीक्षमाणः = प्रति + ईक्ष् + शानच
(ट) करणीया = कृ + अनीयर् + टाप
(ठ) प्रत्यभिज्ञाय = प्रति + अभि + ज्ञा + ल्यप्
(ड) कारकः = कृ + ण्वुल्
(ढ) कृतवती = क + क्तवतु + ङीप्
(ण) विक्रेता = वि + क्री + तृच

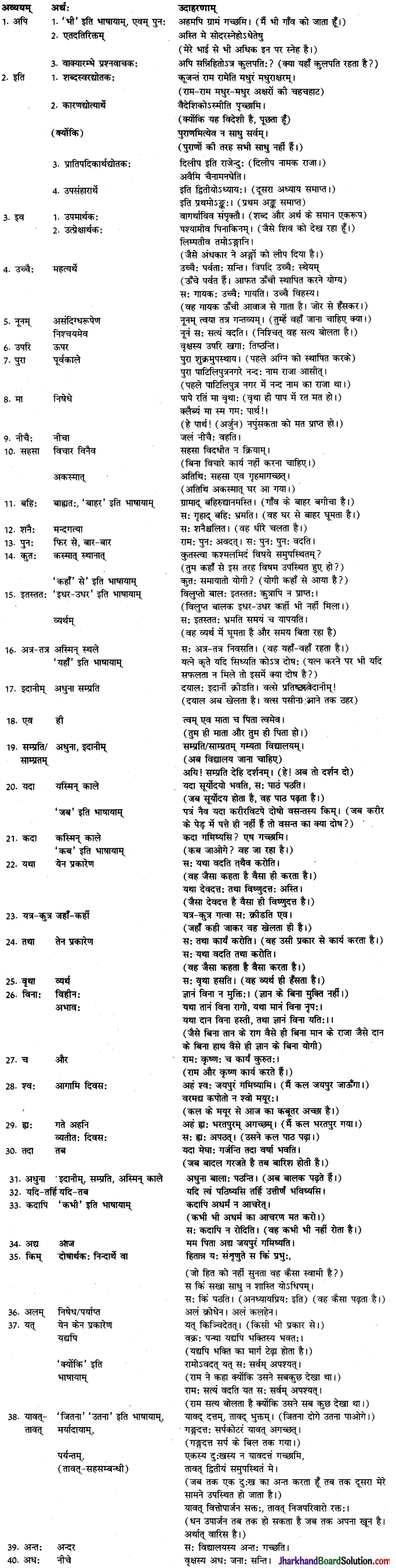
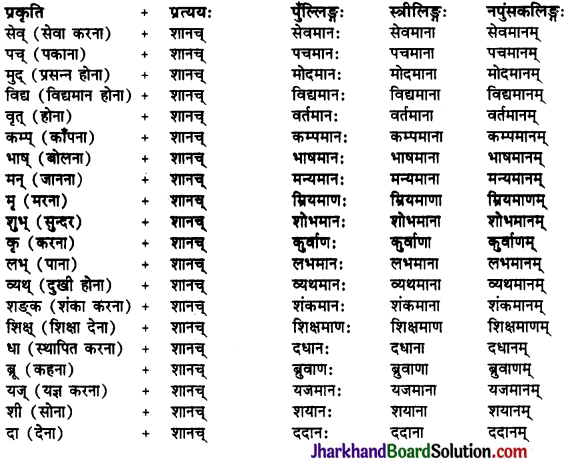
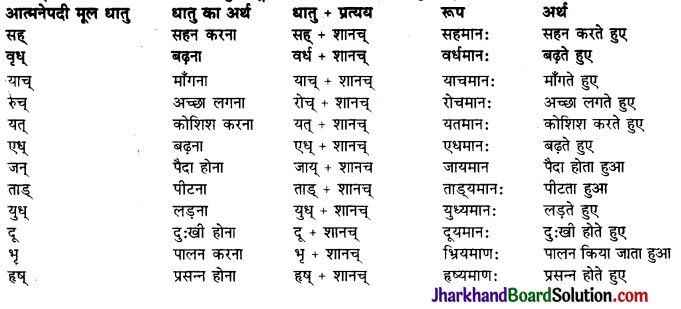
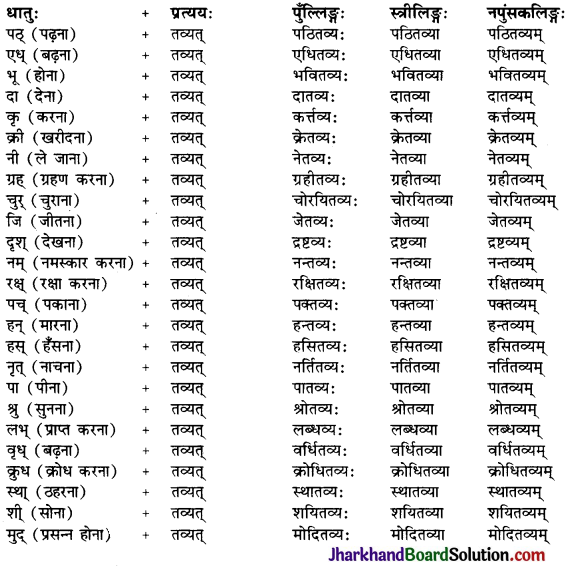
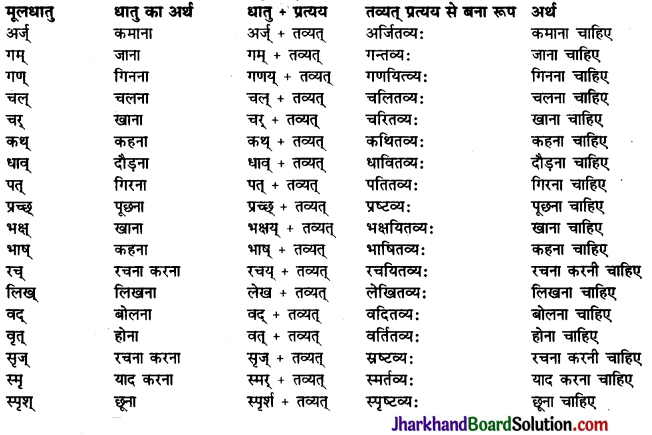
Jharkhand Board JAC Class 10 Sanskrit Solutions व्याकरणम् कारकम् Questions and Answers, Notes Pdf.

JAC Board Class 10th Sanskrit व्याकरणम् कारकम्

कारकस्य परिभाषा – क्रियाजनकं कारकम् अथवा क्रियां करोति इति कारकम्। (क्रिया का जनक कारक होता है अथवा क्रिया को करता है वह कारक है।)

अर्थात् यः क्रियां सम्पादयति अथवा यस्य क्रियया सह साक्षात् परम्परया वा सम्बन्धो भवति सः ‘कारकम्’ इति कथ्यते। (अर्थात् जो क्रिया को सम्पादित करता है अथवा जिसका क्रिया के साथ साक्षात् अथवा परम्परा से सम्बन्ध होता है वह ‘कारक’ कहा जाता है।)

क्रियया सह कारकाणां साक्षात् परम्परया व सम्बन्धः कथं भवति इति बोधयितुम् अत्र वाक्यमेकं प्रस्तूयते। यथा (क्रिया के साथ कारकों का साक्षात् अथवा परम्परा से सम्बन्ध कैसे होता है यह जानने के लिए यहाँ एक वाक्य प्रस्तुत किया जा रहा है।)

“हे मनुष्याः! नरदेवस्य पुत्रः जयदेवः स्वहस्तेन कोषात् निर्धनेभ्यः ग्रामे धनं ददाति।” अत्र क्रियया सह कारकाणां सम्बन्धं ज्ञातुम् एवं प्रकारेण प्रश्नोत्तरमार्गः आश्रयणीय: (यहाँ क्रिया के साथ कारकों का सम्बन्ध जानने के लिए इस प्रकार से प्रश्नोत्तर मार्ग का आश्रय लेना चाहिए-)

एवमेव जयदेवः इति कर्तृकारकस्य तु क्रियया सह साक्षात् सम्बन्धः अस्ति अन्येषां कारकाणां च परम्परयां सम्बन्धः अस्ति। अतः इमानि सर्वाणि कारकाणि कथ्यन्ते। परन्तु अस्य एव वाक्यस्य हे मनुष्याः, नरदेवस्य च इति पदद्वयस्य ‘ददाति’ इति क्रियया सह साक्षात् परम्परया वा सम्बन्धो नास्ति। अतः इदं पदद्वयं कारकम् नास्ति। सम्बन्धः कारकं तु नास्ति परन्तु तस्मिन् षष्ठी विभक्तिः भवति। (इसी प्रकार ‘जयदेव’ इस कर्ता कारक का तो क्रिया के साथ साक्षात् सम्बन्ध है और दूसरे कारकों का परम्परा से सम्बन्ध है। अतः ये सब कारक कहे जाते हैं। परन्तु इस वाक्य का “हे मनुष्याः , नरदेवस्य” इन दो पदों का ‘ददाति’ क्रिया के साथ साक्षात् अथवा परम्परा से सम्बन्ध नहीं है। अतः ये दो पद कारक नहीं हैं। सम्बन्ध कारक तो नहीं हैं परन्तु उसमें षष्ठी विभक्ति होती है।)

कारकाणां संख्या- इत्थं कारकाणां संख्या षड् भवति। यथोक्तम्- (इस प्रकार कारकों की संख्या छः होती है। जैसा कहा है-)

कर्ता कर्म च करणं च सम्प्रदानं तथैव च।
अपादानाधिकरणमित्याहुः कारकाणि षट्।।

अत्र कारकाणां विभक्तीनां च सामान्यपरिचयः प्रस्तूयते- (यहाँ कारकों और विभक्तियों का सामान्य परिचय प्रस्तुत किया जा रहा है-)

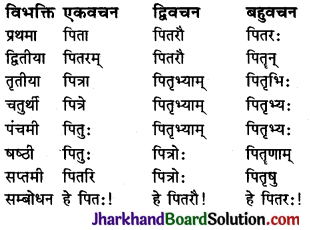
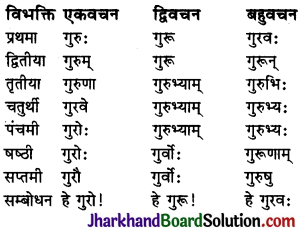
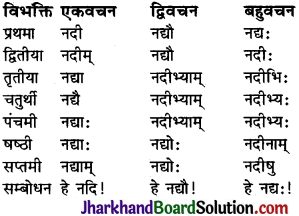
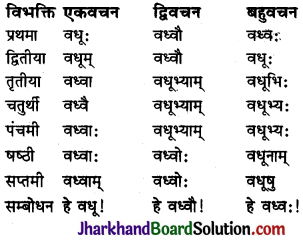
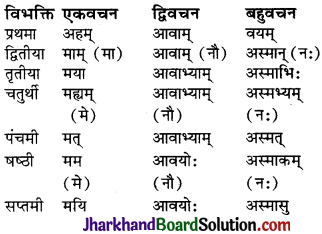
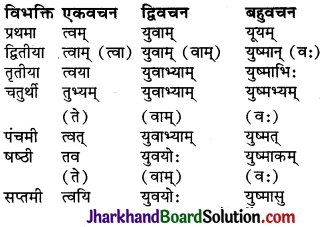
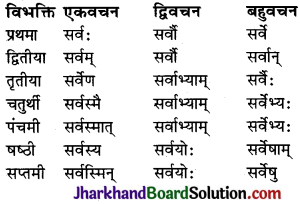
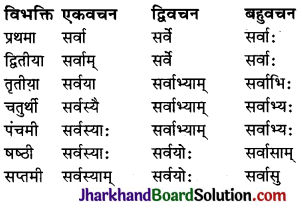
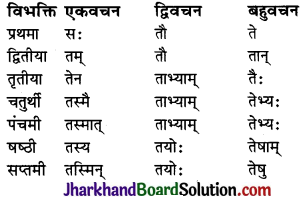
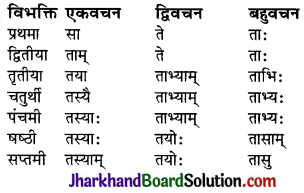
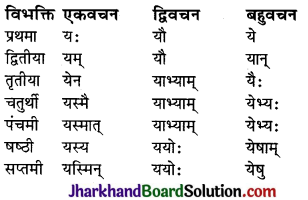
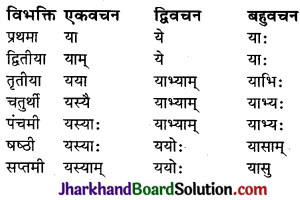
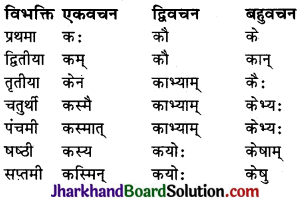
ध्यातव्यः – संस्कृत में प्रथमा से सप्तमी तक सात विभक्तियाँ होती हैं। ये सात विभक्तियाँ ही कारक का रूप धारण करती हैं। सम्बोधन विभक्ति को प्रथमा विभक्ति के ही अन्तर्गत गिना जाता है। क्रिया से सीधा सम्बन्ध रखने वाले शब्दों को ही कारक माना गया है। षष्ठी विभक्ति का क्रिया से सीधा सम्बन्ध नहीं होता है, अतः ‘सम्बन्ध’ कारक को कारक नहीं माना गया है। इस प्रकार संस्कृत में कारक छः ही होते हैं तथा विभक्तियाँ सात होती हैं। कारकों में प्रयुक्त विभक्तियों तथा उनके चिह्नों का विवरण इस प्रकार है –

प्रथमा-विभक्तिः

यः क्रियायाः करणे स्वतन्त्रः भवति सः कर्ता इति कथ्यते (स्वतन्त्रः कर्ता)। उक्तकर्तरि च प्रथमा विभक्तिः भवति। यथा-रामः पठति। (जो क्रिया के करने में स्वतन्त्र होता है, वह कर्ता कहा जाता है। (स्वतन्त्र कर्ता) और कर्ता में प्रथमा विभक्ति होती है। जैसे- रामः पठति।)

अत्र पठनक्रियायाः स्वतन्त्ररूपेण सम्पादकः रामः अस्ति। अतः अयम् एव कर्ता अस्ति। कर्तरि च प्रथमा विभक्तिः भवति। (यहाँ पठन क्रिया का स्वतन्त्र रूप से सम्पादन करने वाला ‘राम’ है। अत: यही कर्ता है और कर्त्ता में प्रथमा विभक्ति होती है।)

कर्मवाच्ये कर्मणि प्रथमा विभक्तिः भवति। (कर्मवाच्य में कर्म में प्रथमा विभक्ति होती है।) यथा- मया ग्रन्थः पठ्यते।

सम्बोधने प्रथमा विभक्तिः भवति (सम्बोधने च) ((सम्बोधन में प्रथमा विभक्ति होती है। ) यथा- हे बालकाः! यूयं कुत्र गच्छथ?

कस्यचित् संज्ञादिशब्दस्य (प्रातिपदिकस्य) अर्थं, लिङ्ग, परिमाणं, वचनं च प्रकटीकर्तुं प्रथमायाः विभक्तेः प्रयोगः क्रियते। यतोहि विभक्तेः प्रयोगं विना कोऽपि शब्दः स्वकीयमर्थं दातुं समर्थो नास्ति अत एव अस्मिन् विषये प्रसिद्ध कथनमस्ति- ‘अपदं न प्रयुञ्जीत।’

उदाहरणार्थम् – बलदेवः, पुरुषः, लघुः, लता। (किसी संज्ञा आदि शब्द के (प्रातिपदकस्य) अर्थ, लिङ्ग, परिमाण और वचन प्रकट करने के लिए प्रथमा विभक्ति का प्रयोग किया जाता है। क्योंकि विभक्ति के प्रयोग के बिना कोई भी शब्द अपना अर्थ देने में समर्थ नहीं है, इसलिए इस विषय में प्रसिद्ध कथन है- “अपदं न प्रयुञ्जीत” उदाहरण के लिए- बलदेवः, पुरुषः, लघुः, लता।)

‘इति’ शब्दस्य योगे प्रथमा विभक्तिः भवति। यथा- वयम् इम् जयन्तः इति नाम्ना जानीमः। (‘इति’ शब्द के प्रयोग में प्रथमा होती है। जैसे- “हमें इसे ‘जयन्त’ इस नाम से जानते हैं।”)

ध्यातव्यः
संस्कृत में कर्ता के तीन पुरुष, तीन वचन और तीन लिङ्ग होते हैं। यथा (जैसे) –

प्रथम पुरुष के सर्वनाम रूपों की भाँति ही राम, लता, फल, नदी आदि के रूप तीनों वचनों में प्रयोग में लाये जाते हैं। कर्ता के तीन लिङ्ग-पुल्लिङ्ग, स्त्रीलिङ्ग तथा नपुंसकलिङ्ग होते हैं। वाक्य में सामान्य रूप से कर्ता कारक को प्रथमा विभक्ति द्वारा व्यक्त करते हैं।

वाक्य में कर्ता की स्थिति के अनुसार संस्कृत में वाक्य तीन प्रकार के होते हैं –
(i) कर्तृवाच्य
(ii) कर्मवाच्य
(iii) भाववाच्य।

(i) कर्तृवाच्यः – जब वाक्य में कर्ता की प्रधानता होती है, तो कर्ता में सदैव प्रथमा विभक्ति ही होती है। जैसे-मोहनः पठति।
(ii) कर्मवाच्यः – वाक्य में कर्म की प्रधानता होने पर कर्म में प्रथमा विभक्ति होती है और कर्त्ता में तृतीया। जैसे-रामेण ग्रन्थः पठ्यते।
(iii) भाववाच्यः – वाक्य में भाव (क्रियातत्त्व) की प्रधानता होती है और कर्म नहीं होता है। कर्ता में सदैव तृतीया विभक्ति और क्रिया (आत्मनेपदी) प्रथम पुरुष एकवचन की प्रयुक्त होती है। जैसे-कमलेन गम्यते।

वाक्य में कर्ता के अनुसार ही क्रिया का प्रयोग किया जाता है अर्थात् कर्ता जिस पुरुष और वचन का होता है, क्रिया भी उसी पुरुष व वचन की होती है।

द्वितीया विभक्तिः

कर्तरीप्सिततमं कर्म – (i) कर्ता क्रियया यं सर्वाधिकम् इच्छति तस्य कर्मसंज्ञा भवति। कर्मणि च द्वितीया विभक्तिः भवति (कर्मणि द्वितीया) कर्ता क्रिया से (क्रिया के द्वारा) जिसे सबसे अधिक चाहता है उसकी कर्म संज्ञा होती है।
“कर्मणि द्वितीया” और कर्म में द्वितीया विभक्ति होती है।) यथा –

रामः ग्रामं गच्छति। (राम गाँव को जाता है।)
बालका: वेदं पठन्ति। (बालक वेद पढ़ते हैं।)
वयं नाटकं द्रक्ष्यामः। (हम नाटक देखेंगे।)
साधुः तपस्याम् अकरोत्। (साधु ने तपस्या की।)
सन्दीपः सत्यं वदेत्। (सन्दीप सत्य बोले।)

(ii) तथायुक्तं अनीप्सितम्-कर्ता जिसे प्राप्त करने की प्रबल इच्छा रखता है, उसे ईप्सितम् कहते हैं और जिसकी इच्छा नहीं रखता उसे अनीप्सित कहते हैं। अनीप्सित पदार्थ पर क्रिया का फल पड़ने पर उसकी कर्म संज्ञा होती है। जैसे-‘दिनेशः विद्यालयं गच्छन्, बालकं पश्यति’ (‘दिनेश विद्यालय को जाता हुआ, बालक को देखता है’) इस वाक्य में ‘बालक’ अनीप्सित पदार्थ है, फिर भी ‘विद्यालयं’ की तरह प्रयुक्त होने से उसमें कर्म कारक का प्रयोग हुआ है।

अधोलिखितशब्दानां योगे द्वितीयाविभक्तिः भवति। यथा – (निम्नलिखित शब्दों के योग में द्वितीय विभक्ति होती है। जैसे-)

अभित:/उभयतः (दोनों) – राजमार्गम् अभितः वृक्षाः सन्ति। (राजमार्ग (सड़क) के दोनों ओर वृक्ष हैं।)
परित:/सर्वतः (चारों ओर): – ग्रामं परितः क्षेत्राणि सन्ति। (गाँव के चारों ओर खेत हैं।)
समया/निकषा (समीप में) – विद्यालयं निकषा देवालयः अस्ति। (विद्यालय के समीप में देवालय है।)
अन्तरेण/विना (बिना) – प्रदीपः पुस्तकं विना/अन्तरेण पठति। (प्रदीप पुस्तक के बिना पढ़ता है।)
अन्तरा (बीच में) – रामं श्यामं च अन्तरा देवदत्तः अस्ति। (राम और श्याम के बीच में देवदत्त है।)
धिक् (धिक्कार) – दुष्टं धिक्। (दुष्ट को धिक्कार है।)
हा (हाय) – हा दुर्जनम् ! (हाय दुर्जन।)
प्रति (ओर) – छात्राः विद्यालयं प्रति गच्छन्ति। (छात्र विद्यालय की ओर जाता है।)
अनु (पीछे) – राजपुरुषः चौरम् अनुधावति। (राजपुरुष चोर के पीछे दौड़ता है।)
यावत् (तक) – गणेशः वनं यावत् गच्छति। (गणेश वन तक जाता है।)
अधोऽधः (सबसे नीचे) भूमिम् अधोऽधः जलम् अस्ति। (भूमि के सबसे नीचे जल है।)
अध्यधि (अन्दर-अन्दर) – लोकम् अध्यधि हरिः अस्ति। (लोक (संसार) के अन्दर-अन्दर हरि है।)
उपर्युपरि (ऊपर-ऊपर) – लोकम् उपर्युपरि सूर्यः अस्ति। (लोक (संसार) के ऊपर-ऊपर सूर्य है।)

अधि – उपसर्गपूर्वक-शीङ्-स्था-आस् धातूनां प्रयोगे एषाम् आधारस्य कर्मसंज्ञा भवति, कर्मणि च द्वितीया विभक्तिः भवति (अधिशीङ्स्थासां कर्म)। उदाहरणार्थम्- (“अधिशीस्थासां कर्म” ‘अधि’ ‘उपसर्गपूर्वक शी। ‘स्था’ (ठहरना) एवं अस्’ (बैठना) धातुओं के प्रयोग में इनके आधार की कर्म संज्ञा होती है और कर्म में द्वितीया विभक्ति होती है। उदाहरण-)

1. अधिशेते (सोता है) – सुरेशः शय्याम् अधिशेते। (सुरेश शैय्या पर सोता है।)
2. अधितिष्ठति (बैठता है) – अध्यापकः आसन्दिकाम् अधितिष्ठति। (अध्यापक कुर्सी पर बैठता है।)
3. अध्यास्ते (बैठता है) – नृपः सिंहासनम् अध्यास्ते। (राजा सिंहासन पर बैठता है।)

उप-अधि-आङ् (आ)- उपसर्गपूर्वक-वस् धातोः प्रयोगे अस्य आधारस्य कर्मसंज्ञा भवति, कर्मणि च द्वितीया विभक्तिः भवति (उपान्वध्यावास:)। (उपान्वध्यावास” उप, अधि, आङ् (अ) उपसर्गपूर्वक ‘वस्’ धातु के प्रयोग में इसके आधार की कर्म संज्ञा होती है। अर्थात् वस धातु से पहले उप, अनु, अधि और आङ् (आ) उपसर्गों में से कोई भी उपसर्ग लगता हो, तो वस् धातु के आधार की कर्म संज्ञा होती है अर्थात् सप्तमी के स्थान पर द्वितीया विभक्ति ही लगती है।

और कर्म में द्वितीया विभक्ति लगती है।)

उपवसति (पास में रहता है) – श्यामः नगरम् उपवसति। (श्याम नगर के पास में रहता है।)
अनुवसति (पीछे रहता है) – कुलदीपः गृहम् अनुवसति। (कुलदीप घर के पीछे रहता है।)
अधिवसति (में रहता है) – सुरेशः जयपुरम् अधिवसति। (सुरेश जयपुर में रहता है।)
आवसति (रहता है) – हरिः वैकुण्ठम् आवसति। (हरि वैकुण्ठ में रहता है।)

“अभि-नि” उपसर्गद्वयपूर्वक-विश्-धातोः प्रयोगे सति अस्य आधारस्य कर्म-संज्ञा भवति, कर्मणि च द्वितीया विभक्तिः भवति (अभिनिविशश्च)। (“अभिनिविशश्च” विश् धातु के प्रयोग के “अधि और नि” ये दो उपसर्ग लगने पर इसके आधार की कर्म संज्ञा होती है और कर्म में द्वितीया विभक्ति होती है।)
अभिनिविशते (प्रवेश करता है) – दिनेशः ग्रामम् अभिनिविशत। (दिनेश ग्राम में प्रवेश करता है।)

अपादानादिकारकाणां यत्र अविवक्षा अस्ति तत्र तेषां कर्मसंज्ञा भवति, कर्मणि च द्वितीयाविभक्तिः भवति (अकथितं च)। संस्कृतभाषायां एतादृशः षोडशधातवः सन्ति येषां प्रयोग एकं तु मुख्यं द्वितीया विभक्तिः भवति। इमे धातवः एक द्विकर्मकधातवः कथ्यन्ते। एतेषां प्रयोगः अत्र क्रियते- (“अकथितं च” अपादान आदि कारकों की जहाँ अविवक्षा हो वहाँ उनकी कर्म संज्ञा होती है और कर्म में द्वितीया विभक्ति होती है। संस्कृत भाषा में इस तरह की सोलह धातुएँ हैं उनके प्रयोग में एक तो मुख्य कर्म होता है और दूसरा अपादान आदि कारक से अविवक्षित गौण कर्म होता है। इस गौण कर्म में भी द्वितीया विभक्ति होती है। ये धातुएँ ही द्विकर्मक धातुएँ कही जाती हैं। इनका प्रयोग यहाँ किया जा रहा है-)

दुह् (दुहना) – गोपाल: गां दोग्धि। (गोपाल गाय से दूध दुहता है)।
याच् (माँगना) – सुरेशः महेशं पुस्तकं याचते। (सुरेश महेश से पुस्तक माँगता है)
पच (पकाना) – याचकः तण्डुलान् ओदनं पचति। (पाचक चावलों से भात पकाता है)
दण्ड् (दण्ड देना) – राजा गर्गान् शतं दण्डयति। (राजा गर्गों को सौ रुपये का दण्ड देता है)
प्रच्छ (पूछना) – सः माणवकं पन्थानं पृच्छति। (वह बालक से मार्ग पूछता है)
रुध् (रोकना) – ग्वालः व्रजं ग्राम अवरुणद्धि। (ग्वाला गाय को व्रज में रोकता है)
चि (चुनना) – मालाकारः लतां पुष्पं चिनोति। (माली लता से पुष्प चुनता है।)
जि. (जीतना) – नृपः शत्रु राज्यं जयति। (राजा शत्रु से राज्य को जीतता है)
ब्रु (बोलना) – गुरु शिष्यं धर्म ब्रूते/शास्ति। (गुरु शिष्य से धर्म कहता है।)
शास् (कहना) गुरु शिष्यं धर्मं ब्रूते/शास्ति। (गुरु शिष्य से धर्म कहता है।)
मथ् (मथना) – सः क्षीरनिधिं सुधां मध्नाति। (वह क्षीरसागर से अमृत मथता है)
मुष् (चुराना) चौरः देवदत्तं धनं मुष्णाति। (चोर देवदत्त से धन चुराता है।)
नी (ले जाना).. – सः अजां ग्रामं नयति। (वह बकरी को गाँव ले जाता है)
ह (हरण करना). – सः कृपणं धनं हरित। (वह कंजूस के धन को हरता है)
वह (ले.जाना) – कृषकः ग्रामं भारं वहति। (किसान गाँव में बोझा ले जाता है)
कृष् (खींचना) – कृषकः क्षेत्र महिर्षी कर्षति। (किसान खेत में भैंस को खींचता है)

कालवाचिनि शब्दे मार्गवाचिनि शब्द च अत्यन्तसंयोगे गम्यमाने द्वितीया विभक्तिः भवति-(कालाध्वनोरत्यन्तसंयोग)। (कालाध्वनोरत्यन्तसंयोग कालवाची शब्द में और मार्गवाची शब्द में अत्यन्त संयोग हो तो कालवाची और मार्गवाची शब्दों में द्वितीया विभक्ति आती है। जैसे-)

सुरेशः अत्र पञ्चदिनानि पठति। (सुरेश यहाँ लगातार पाँच दिन से पढ़ रहा है)
मोहनः मासम् अधीते। (मोहन लगातार महीने भर पढ़ता है)
नदी क्रोशं कुटिला अस्ति। (नदी कोस भर तक लगातार टेढ़ी है)
प्रदीपः योजनं पठति। (प्रदीप लगातार एक योजन तक पढ़ता।

ध्यातव्य –

“गत्यर्थककर्मणि द्वितीयचतुझे चेष्टायामध्वनि” यदा गत्यर्थक धातुनां कर्मः मार्ग न भवति तदां चतुर्थी द्वितीया। च भवति। यथा (अर्थात् जब गति अर्थ वाली धातुओं का कर्म मार्ग नहीं रहता, तब चतुर्थी और द्वितीया विभक्ति होती है। जैसे- ‘गृहं गृहाय वा गच्छति’ यहाँ जाने में हाथ-पैर आदि अंगों का हिलना-डुलना रहा और गृह मार्ग नहीं है। मार्ग में द्वितीया होती है- ‘पन्थानं गच्छति’ शरीर के व्यापार न करने पर – ‘चेतसां हरि ब्रजति’ (मन से ईश्वर (हरि) को भजता है)।
उदाहरण –
(i) रामः ग्रामं गच्छति। (राम गाँव को जाता है।)
(ii) सिंह वनं विचरति। (सिंह वन में विचरण करता है।)
(iii) स स्मृतिं गच्छति। (वह स्मृति को प्राप्त करता है।)
(iv) स परं विषादम् अगच्छत्। (वह परम विषाद को प्राप्त हुआ।)

“एनपा द्वितीया” अर्थात् एनप् प्रत्ययान्तस्य शब्दस्य येन समीपता प्रतीतं भवति, तस्मिन् द्वितीया षष्ठी वा भवति। यथा – (अर्थात् एनप् प्रत्ययान्त शब्द की जिससे समीपता प्रतीत होती है, उसमें द्वितीया अथवा षष्ठी विभक्ति होती हैं। जैसे-)
1. नगरं नगरस्य व दक्षिणेन (नगर के दक्षिण की ओर)
2. उत्तरेण यमुनाम् (यमुना के उत्तर में)

तृतीया विभक्तिः

(क) क्रियासिद्धौ यत् सर्वाधिकं सहायकं भवति तस्य कारकस्य करणसंज्ञा भवति (साधकतमं करणम्)। कतरि करणे च (कर्तृकरणयोस्तृतीया इति पाणिनीय सूत्रेण) तृतीया विभक्तिः भवति। यथा- (कार्य की सिद्धि में जो सबसे अधिक सहायक होता है उस कारक की ‘करण’ संज्ञा होती है। (साधकतमं करणम्।)
“कर्तृकरणयोस्तृतीया” इस पाणिनीय सूत्र से (भाववाच्य अथवा कर्मवाच्य के) कर्ताकारक में तथा करा . कारक में तृतीया विभक्ति होती है। जैसे-)
1. जागृतिः कलमेन लिखति।
(जागृति कलम से लिखती है।)

2. वैशाली जलेन मुखं प्रक्षालयति।
(वैशाली जल से मुँह धोती है।)

3. रामः दुग्धेन रोटिकां खादति।
(राम दूध से रोटी खाता है।)

4. सुरेन्द्रः पादाभ्यां चलति।
(सुरेन्द्र पैरों से चलता है।)

(ख) कर्मवाच्यस्य भाववाच्यस्य वा अनुक्तकर्तरि अपि तृतीया विभक्ति भवति। यथा (कर्मवाच्य अथवा भाववाच्य के अनुक्त कर्ता में भी तृतीया विभक्ति होती है जैसे-)

1. रामेण लेखः लिख्यते। (कर्मवाच्ये)
(राम के द्वारा लेख लिखा जाता है।)

2. मया जलं पीयते। (कर्मवाच्ये)
(मेरे द्वारा जल पीया जाता है।)

3. तेन हस्यते। (भाववाच्ये)
(उसके द्वारा हँसा जाता है।)

सह-साकम्-समम्-साधर्म-शब्दानां योगे तृतीया विभक्तिः भवति (सहयुक्तेऽप्रधाने)। यथा –
“सहयुक्तोऽप्रधाने” अर्थात् सह-साकम्, समम्, सार्धम् शब्दों के योग में तृतीया विभक्ति होती है। जैसे-)

1. जनकः पुत्रेण सह गच्छति।
(पिता पुत्र के साथ जाता है।)

2. सीता गीतया साकं पठति।
(सीता गीता के साथ पढ़ती है।)

3. ते स्वमित्रैः सार्धं क्रीडन्ति।
(वे अपने मित्रों के साथ खेलते हैं।)

4. त्वं गुरुणा सह वेदपाठं करोषि।
(तुम गुरु के साथ वेदपाठ करते हो।)

येन विकृतेन अङ्गेन अङ्गिनः विकारो लक्ष्यते तस्मिन् विकृताङ्गे तृतीया भवति (येनाङ्गविकार:)। यथा –
(“येनाङ्गविकारः” अर्थात जिस विकृत अङ्ग से अङ्ग विकार लक्षित होता है उस विकृत अङ्ग में तृतीया विभक्ति होती है। जैसे-)

1. सः नेत्रेण काणः अस्ति।
(वह आँख से काना है।)

2. बालकः कर्णेन बधिरः वर्तते।
(बालक कान से बहरा है।)

3. साधुः पादेन खञ्जः अस्ति।
(साधु पैर से लगड़ा है।)

4. श्रेष्ठी शिरसा खल्वाट: विद्यते।
(सेठ शिर से गंजा है।)

5. सूरदासः नेत्राभ्याम् अन्धः आसीत्।
(सूरदास आँखों से अन्धा था।)

येन चिह्नेन कस्यचिद् अभिज्ञानं भवति तस्मिन् चिह्नवाचिनि शब्दे तृतीया विभक्तिः भवति (इत्थंभूतलक्षणे)। यथा –
(“इत्थंभूतलक्षणे”.अर्थात् जिस चिह्न से किसी का ज्ञान होता है उस चिह्नवाची शब्द में तृतीया विभक्ति होती है। जैसे-)

1. सः जटाभिः तापसः प्रतीयते।।
(वह जटाओं से तपस्वी प्रतीत होता है।)

2. सः बालकः पुस्तकैः छात्रः प्रतीयते।
(वह बालक पुस्तकों से छात्र प्रतीत होता है।)

हेतुवाचिशब्दे तृतीया विभक्तिः भवति (हेतौ) यथा –
(हेतुवाची शब्द में तृतीया विभक्ति होती है। जैसे-)

1. पुण्येन हरिः दृष्टः।
(पुण्य से हरि को देखा।)

2. सः अध्ययनेन वसति।
(वह पढ़ने हेतु रहता है।)

3. विद्यया यशः वर्धते।
(विद्या से यश बढ़ता है।)

4. विद्या विनयेन शोभते।।
(विद्या विनय से शोभा पाती है।)

प्रकृति-आदिक्रियाविशेषणशब्देषु तृतीया विभक्तिः भवति (प्रकृत्यादिभ्यः उपसंख्यानम्)।
(“प्रकृत्यादिभ्यः उपसंख्यानाम्” प्रकृति आदि क्रियाविशेषण शब्दों में तृतीया विभक्ति होती है। जैसे-)

1. सः प्रकृत्य साधुः अस्ति।
(वह प्रकृति से साधु (सज्जन) है।)

2. गणेशः सुखेन जीवति।
(गणेश सुख से जीता है।)

3. प्रियंका सरलतया लिखति।
(प्रियंका सरलता से लिखती है।)

4. मूर्खः दुःखेन जीवति।
(मूर्ख दुःख से जीता है।)

निषेधार्थकस्य अलम् इति शब्दस्य योगे तृतीया विभक्तिः भवति। यथा –
(निषेधार्थक ‘अलम्’ शब्द के योग में तृतीया विभक्ति होती है। जैसे-)

1. अलं हसितेन। (हँसो मत)।
अलं विवादेन। (विवाद मत करो)

चतुर्थी विभक्तिः

दानस्य कर्मणा कर्ता यं सन्तुष्टं कर्तुम् इच्छति सः सम्प्रदानम् इति कथ्यते (कर्मणा यमभिप्रेति स सम्प्रदानम्), सम्प्रदाने च (चतुर्थी सम्प्रदाने इति पाणिनीयसूत्रेण) चतुर्थी विभक्तिः भवति। यथा –
(“कर्मण यमभिप्रेति स सम्प्रदानम्” अर्थात् दान के कर्म के द्वारा कर्ता जिसे सन्तुष्ट करना चाहता है, वह पदार्थ सम्प्रदान कहलाता है।
“चतुर्थी सम्प्रदाने” इस पाणिनीय सूत्र से सम्प्रदान में चतुर्थी विभक्ति होती है। जैसे-)

1. नृपः निर्धनाय धनं यच्छति। (राजा निर्धन को धन देता है।)
2. बालकः स्वमित्राय पुस्तकं ददाति। (बालक अपने मित्र को पुस्तक देता है।)

रुच्यर्थानां धातूनां प्रयोगे यः प्रीयमाणः भवति तस्य सम्प्रदानसंज्ञा भवति, सम्प्रदाने च चतुर्थी विभक्तिः भवति (रुच्यर्थानां प्रीयमाणः)। यथा – (“रुच्यर्थानां प्रीयमाण:” रुच तथा रुच् के अर्थवाली धातुओं के योग में जो प्रसन्न होता है उसकी सम्प्रदान संज्ञा होती है, सम्प्रदान में चतुर्थी विभक्ति होती है। जैसे-)

1. भक्ताय रामायणं रोचते।
(भक्त को रामायण अच्छी लगती है।)

2. बालकाय मोदकाः रोचन्ते।।
(बालक को लड्डू अच्छे लगते हैं।)

3. गणेशाय दुग्धं स्वदते।
(गणेश को दूध अच्छा लगता है।)

क्रुधादि-अर्थानां धातूनां प्रयोगे यं प्रति कोपादिकं क्रियते तस्य सम्प्रदानसंज्ञा भवति, सम्प्रदाने च चतुर्थी विभक्तिः भवति (क्रुधदुहेासूयार्थानां यं प्रति कोपः)। (‘क्रुधदुहेासूयार्थानां यं प्रति कोपः’ क्रुध आदि अर्थों की धातुओं के (क्रुध्, द्रुह, ईर्ष्ण, असूय) प्रयोग में जिस पर कोप (क्रोध) आदि किया जाता है, उसकी सम्प्रदान संज्ञा होती है और सम्प्रदान में चतुर्थी विभक्ति होती है। जैसे-)

1. क्रुध् (क्रोध करना) – पिता पुत्राय क्रुध्यति। (पिता पुत्र पर क्रोध करता है।)
2. द्रह (द्रोह करना) – किंकरः नपाय द्रहयति। (नौकर राजा से द्रोह करता है।)
3. ईर्ष्या (ईर्ष्या करना) – दुर्जनः सज्जनाय ईर्ण्यति। (दुर्जन सज्जन से ईर्ष्या करता है।)
4. असूय् (निन्दा करना) – सुरेशः महेशाय असूयति। (सुरेश महेश की निन्दा करता है।

स्पृह (ईप्सायां) धातोः प्रयोगे यः ईप्सितः भवति तस्य सम्प्रदानसंज्ञा भवति, सम्प्रदाने च चतुर्थी विभक्तिः भवति (स्पृहेरीप्सितः)। यथा – (स्पृह (चाहना) धातु के प्रयोग में (जिसे चाहा गया है) जो ईप्सित (प्रिय) होता है उसकी सम्प्रदान संज्ञा होती है, सम्प्रदान में चतुर्थी विभक्ति होती है। जैसे-)
1. स्पृह (इच्छा करना) – बालकः पुष्पाय स्पृह्यति। (बालक पुष्प की इच्छा करता है।)

नमः, स्वस्ति, स्वाहा, स्वधा, अलम्, वषट्, इति शब्दानां योगे चतुर्थी विभक्तिः भवति (नमः स्वस्तिस्वाहास्व धालंवषड्योगाच्च)। यथा- (“नमः स्वस्तिस्वहास्वधालंवषड्योगाच्च” नमः, स्वस्ति, स्वाहा, स्वधा, अलम्, वषट इन शब्दों के योग में चतुर्थी विभक्ति होती है। जैसे-)

1. नमः (नमस्कार) – रामाय नमः। (राम को नमस्कार)
2. स्वस्ति (कल्याण)। – गणेशाय स्वस्ति। (गणेश का कल्याण हो।)
3. स्वाहा (आहुति) प्रजापतये स्वाहा। . (प्रजापति के लिए आहुति)
4. स्वधा ” स्वधा (हवि का दान) – पितभ्यः स्वधा। (पितरों के लिए हवि का दान)
5. वषट् (हवि का दान) – सूर्याय वषट्। (सूर्य के लिए हवि का दान)
6. अलम् (समर्थ) – दैत्येभ्यः हरिः अलम्। (दैत्यों के लिए हरि पर्याप्त हैं।)

धृञ् (धारणे) धातोः प्रयोगे यः उत्तमर्णः (ऋणदाता) भवति तस्य सम्प्रदान संज्ञा स्यात्, सम्प्रदाने च चतुर्थी विभक्तिः , भवति (धारेरुत्तमर्णः)। यथा- (“धारेरुत्तमर्णः” धृञ् धारण करना धातु के योग में जो उत्तमर्ण (ऋणदाता) होता है उसकी सम्प्रदान संज्ञा होवे, सम्प्रदान में चतुर्थी विभक्ति होती है। जैसे-)
देवदत्तः यज्ञदत्ताय शतं धारयति। (देवदत्त यज्ञदत्त का सौ रुपये का ऋणी है।)

यस्मै प्रयोजनाय या क्रिया क्रियते तस्मिन् प्रयोजनवाचिनि शब्दे चतुर्थी विभक्तिः भवति (तादर्थ्य चतुर्थी वाच्या)।
यथा – (“तादर्थं चतुर्थी वाच्या” जिस प्रयोजन के लिए जो क्रिया की जाती है उसके प्रयोजन वाची शब्द में चतुर्थी विभक्ति होती है जैसे-)

1. सः मोक्षाय हरि भजति। (वह मोक्ष के लिए हरि को भजता है।)
2. बालकः दुग्धाय क्रन्दति। (बालक दूध के लिए रोता है।)

निम्नलिखितधातूनां योगे प्रायः चतुर्थी विभक्तिः भवति। यथा- (निम्नलिखित धातुओं के योग में प्रायः चतुर्थी विभक्ति
होती है। जैसे-)
1. कथय (कहना) – रामः स्वमित्राय कथयति। (राम अपने मित्र के लिए कहता है।)
2. निवेदय् (निवदेन करना) – शिष्यः गुरुवे निवेदयति। (शिष्य गुरु से निवेदन करता है।)
3. उपदिश् (उपदेश देना) – साधुः सज्जनाय उपदिशति। (साधु सज्जन के लिए उपदेश देता है।)

पञ्चमी विभक्तिः

अपाये सति यद् ध्रुवं तस्य अपादानसंज्ञा भवति (ध्रुवमपायेऽपादानम्), अपादाने च (अपादाने पञ्चमी इति सूत्रेण)
पञ्चमी विभक्तिः भवति। यथा – (“ध्रुवमपायेऽपादानम्” जिससे कोई वस्तु पृथक् (अलग) हो, उसकी अपादान संज्ञा होती है और “अपादाने पञ्चमी” इस सूत्र से अपादान में पंचमी विभक्ति होती है। जैसे-)

1. वृक्षात् पत्रं पतति।
(वृक्ष से पत्ता गिरता है।)

2. नृपः ग्रामात् आगच्छति।
(नृप गाँव से आता है।)

भयार्थानां रक्षणार्थानां च धातूनां प्रयोगे भयस्य यद् हेतुः अस्ति तस्य आपादान संज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (भीत्रार्थानां भयहेतुः) यथा- (“भीत्रार्थाना भयहेतुः” भय और रक्षा अर्थवाली धातुओं के साथ भय का जो हेतु है उसकी अपादान संज्ञा होती है, अपादान में पञ्चमी विभक्ति होती है। जैसे-)

1. बालकः सिंहात् विभेति।
(बालक सिंह (शेर) से डरता है।)

2. नृपः दुष्टात् रक्षति/त्रायते।
(नृप (राजा) दुष्ट से रक्षा करता है।

यस्मात् नियमपूर्वकं विद्या गृह्यते तस्य शिक्षकादिजनस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (आख्यातोपयोगे)। यथा- (“आख्यातोपयोगे” अर्थात् जिससे नियमपूर्वक विद्या ग्रहण की जाती है उस शिक्षक आदि की अपादान संज्ञा होती है और अपादान में पंचमी विभक्ति होती है। जैसे-)

1. शिष्यः उपाध्यायात् अधीते।
(शिष्य उपाध्याय से पढ़ता है।)

2. छात्रः शिक्षकात् पठति।
(छात्र शिक्षक से पढ़ता है।)

जुगुप्सा-विराम – प्रमादार्थकधातूनां प्रयोगे यस्मात् घृणादि क्रियते तस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (जुगुप्साविरामप्रमादार्थानामुपसंख्यानम्)। यथा – (“जुगुप्साविरामप्रमादार्थानामुपसंख्यानाम्” अर्थात् जुगुप्सा, घृणा करना, विराम (रुकना), प्रमाद (असावधानी करना) अर्थ वाली धातुओं के प्रयोग में जिससे घृणा आदि की जाती है, उसकी अपादान संज्ञा होती है और अपादान में पञ्चमी विभक्ति का प्रयोग होता है। जैसे-)

1. महेशः पापात् जुगुप्सते।
(महेश पाप से घृणा करता है।)

2. कुलदीपः अधर्मात् विरमति।
(कुलदीप अधर्म से रुकता है।)

3. मोहनः अध्ययनात् प्रमाद्यति।
(मोहन अध्ययन में असावधानी (प्रमाद) करता है।)

भूधातोः यः कर्ता, तस्य यद् उत्पत्तिस्थानम्, तस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (भुवः प्रभाव:)। यथा- (“भुवः प्रभावः” अर्थात् भू (होना) धातु के कर्ता का जो उद्गम स्थान होता है, उसकी अपादान संज्ञा होती है और अपादान में पञ्चमी विभक्ति होती है। जैसे-)

1. गंगा हिमालयात् प्रभवति।
(गंगा हिमालय से निकलती है।)

2. काश्मीरात् वितस्ता नदी प्रभवति।
(कश्मीर से वितस्ता नदी निकलती है।)

जन् धातोः यः कर्त्ता, तस्य या प्रकृतिः (कारणम् = हेतुः) तस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (जनिकः प्रकृतिः)। यथा-(“जनिकर्तृः प्रकृतिः” अर्थात् ‘जन’ (उत्पन्न होना) धातु का जो कर्ता है उसके हेतु (करण) की अपादान संज्ञा होती है और अपादान में पञ्चमी विभक्ति होती है। जैसे-)

1. गोमयात् वृश्चिक: जायते।
(गाय के गोबर से बिच्छू उत्पन्न होते हैं।)

2. कामात् क्रोधः जायते।
(काम से क्रोध उत्पन्न होता है।)

कर्ता, यस्मात् अदर्शनम् इच्छति, तस्य कारकस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः भवति (अन्तौँ येनादर्शनमिच्छति)। यथा-” (“अन्तौ येना दर्शनमिच्छति” अर्थात् जब कर्ता जिससे अदर्शनं (छिपना) चाहता है, तब उसे कारक की अपादान संज्ञा होती है और अपादान में पञ्चमी विभक्ति होती है। जैसे –

1. बालकः मातुः निलीयते।
(बालक माता से छिपता है।)

2. महेश: जनकात् निलीयते।
(महेश पिता से छिपता है।)

वारणार्थानां धातूनां प्रयोगे यः ईप्सितः अर्थः भवति तस्य कारकस्य अपादानसंज्ञा भवति, अपादाने च पञ्चमी विभक्तिः
(वारणार्थानामीप्सितः)। यथा- (“वारणार्थानामीप्सितः” अर्थात् वरण (हटाना) अर्थ की धातु के योग में अत्यन्त इष्ट (प्रिय) वस्तु की अपादान संज्ञा होती है और उसमें पञ्चमी विभक्ति होती है। जैसे-) कृषक: यवेभ्यः गां वारयति।
(किसान जौ से गाय को हटाता है।)

यदा द्वयोः पदार्थयोः कस्यचित् एकस्य पदार्थस्य विशेषता प्रदर्श्यते तदा विशेषणशब्दैः सह ईयसुन् अथवा तर प्रत्ययस्य योगः क्रियते, यस्मात् च विशेषता प्रदर्श्यते तस्मिन् पञ्चमी विभक्तेः प्रयोगः भवति (पञ्चमी विभक्ते)। यथा- (“पञ्चमी विभक्तेः” अर्थात् जब दो पदार्थों में से किसी एक पदार्थ की विशेषता प्रकट की जाती है, तब विशेषण शब्दों के साथ “ईयसुन” अथवा “तरप्” प्रत्यय का प्रयोग किया जाता है और जिसमें विशेषता प्रकट की जाती है उसमें पञ्चमी विभक्ति होती है। जैसे-)

1. रामः श्यामात् पटुतरः अस्ति।
(राम श्याम से अधिक चतुर है।)

2. माता भूमेः गुरुतरा अस्ति।
(माता भूमि से अधिक बढ़कर है।)

3. जननी जन्मभूमिश्च स्वर्गात् अपि गरीयसी। (जननी, जन्मभूमि स्वर्ग से भी बढ़ी है।)

अधोलिखितशब्दानां योगे पञ्चमी विभक्तिः भवति। यथा –
(निम्नलिखित के योग में पञ्चमी विभक्ति होती है। जैसे-)

1. ऋत (बिना) – ज्ञानात् ऋते मुक्तिः न भवति। (ज्ञान के बिना मुक्ति नहीं होती हैं।)
2. प्रकृति (से लेकर) – सः बाल्यकालात् प्रभृति अद्यावधि अत्रैव पठति। (वह बाल्यकाल से लेकर आज तक यहाँ ही पढ़ता है।)
3. बहिः (बाहर) छात्राः विद्यालयात् बहिः गच्छति। (छात्र विद्यालय से बाहर जाता है।)
4. पूर्वम् (पहले) – विद्यालयगमनात् पूर्व गृहकार्यं कुरु। (विद्यालय जाने से पहले गृहकार्य करो।)
5. प्राक् (पूर्व) – ग्रामात् प्राक् आश्रमः अस्ति। (ग्राम से पहले आश्रम है।) : अन्य (दूसरा)
6. रामात् अन्यः अयं कः अस्ति? (राम से दूसरा यह कौन है?) Fitik अनन्तरम् (बाद)
7. यशवन्तः पठनात् अनन्तरं क्रीडाक्षेत्रं गच्छति। (यशवन्त पढ़ने के बाद खेल के मैदान में जाता है।)
8. पृथक् (अलग) नगरात् पृथक् आश्रमः अस्ति।
9. परम् (बाद) – रामात् परम् श्यामः अस्ति।

षष्ठी विभक्तिः 

(नगर से पृथक् आश्रम है।) (राम के बाद श्याम है।)

सम्बन्धे षष्ठी विभक्तिः भवति (षष्ठि शेषे)। यथा – (“षष्ठी शेषे सम्बन्ध में षष्ठी विभक्ति होती है। जैसे-)
रमेशः संस्कृतस्य पुस्तकं पठति। (रमेश संस्कृत की पुस्तक पढ़ता है।)

यदा बहुषु कस्यचित् एकस्य जातिगुणक्रियाभिः विशेषता प्रदर्श्यते तदा विशेषणशब्दैः सह इष्ठन् अथवा तमप् प्रत्ययस्य योगः क्रियते यस्मात् च विशेषता प्रदर्श्यते तस्मिन् षष्ठी विभक्तेः अथवा सप्तमीविभक्तेः प्रयोगः भवति (यतश्च निर्धारणम्)। यथा- (“यतश्च निर्धारणम्” अर्थात् जब बहुत में से किसी एक की जाति, गुण, क्रिया के द्वारा विशेषता प्रकट की जाती है, तब विशेषण शब्दों के साथ ‘इष्ठन्’ अथवा ‘तमप्’ प्रत्यय का प्रयोग किया जाता है और जिससे विशेषता प्रकट की जाती है, उसमें षष्ठी विभक्ति अथवा सप्तमी विभक्ति का प्रयोग होता है। जैसे-)

1. कवीनां (कविषु वा) कालिदासः श्रेष्ठ अस्ति। (सभी कवियों में कालिदास सबसे श्रेष्ठ हैं।)
2. छात्राणां (छात्रेषु वा) सुरेशः पटुतमः अस्ति। (सभी छात्रों में सुरेश सबसे अधिक चतुर है।)

अधोलिखितशब्दाना योगे षष्ठीविभक्तिः भवति। यथा – (निम्नलिखित शब्दों के योग में षष्ठी विभक्ति होती है।)

1. अधः (नीचे) – वृक्षस्य अधः बालकः शेते। (वृक्ष के नीचे बालक सोता है।)
2. उपरि (ऊपर) – भवनस्य उपरि खगाः सन्ति। (भवन के ऊपर पक्षी हैं।)
3. पुरः (सामने) – विद्यालयस्य पुरः मन्दिरम् अस्ति। (विद्यालय के सामने मंदिर है।)
4. समक्षम् (सामने) – अध्यापकस्य समक्षं शिष्यः अस्ति। (अध्यापक के समक्ष शिष्य है?)
5. समीपम् (समीप) – नगरस्य समीपं ग्रामः अस्ति। (नगर के समीप ग्राम है।)
6. मध्ये (बीच में) पशूनां मध्ये ग्वालः अस्ति। (पशुओं के बीच में ग्वाला है।)
7. कृते (के लिए) बालकस्य कृते दुग्धम् आनय। (बालक के लिए दूध लाओ।)
8. अन्तः (अन्दर) – गृहस्य अन्तः माता विद्यते। (घर के अन्दर माता है।)

तुल्यवाचिशब्दानां योगे षष्ठि अथवा तृतीया विभक्तिः भवति (तुल्यार्थैरतुलोपमाभ्यां तृतीयान्यतरस्याम्)। यथा –
(“तुल्यार्थैरतुलोपमाभ्यां तृतीयान्यतरस्याम्” अर्थात् तुलनावाची शब्दों के योग में षष्ठी अथवा तृतीया विभक्ति होती है। जैसे-)

1. सुरेशः महेशस्य (महेशे वा) तुल्यः अस्ति। (सुरेश महेश के समान है।)
2. सीता गीतायाः (गीतया वा) तुल्या विद्यते। (सीता गीता के समान है।)

अन्य महत्त्वपूर्ण नियम –

‘षष्ठी हेतु प्रयोगे’ – अर्थात् हेतु शब्द का प्रयोग करने पर प्रयोजनवाचक शब्द एवं हेतु शब्द, दोनों में ही षष्ठी विभक्ति आती है। जैसे –

(i) अन्नस्य हेतोः वसति। (अन्न के कारण रहता है।)
(ii) अल्पस्य हेतोः बहु हातुम् इच्छन्। (थोड़े के लिए बहुत छोड़ने की इच्छा करता हुआ।)

‘षष्ठ्यतसर्थप्रत्ययेन’-अर्थात् दिशावाची अतस् प्रत्यय तथा उसके अर्थ वाले प्रत्यय लगाकर बने शब्दों तथा इसी प्रकार के अर्थ के, पुरस्तात् (सामने), पश्चात् (पीछे), उपरिष्टात् (ऊपर की ओर) और अधस्तात् (नीचे की ओर) आदि शब्दों के योग में षष्ठी विभक्ति होती है। जैसे –
(i) ग्रामस्य दक्षिणत: देवालयोऽस्ति। (गाँव के दक्षिण की ओर मन्दिर है।)
(ii) वृक्षस्य अधः (अधस्ताद् वा) जलम् अस्ति। (वृक्ष के नीचे की ओर जल है।)

‘अधीगर्थदयेषां कर्मणि’-अर्थात् स्मरण अर्थ की धातु के साथ कर्म में षष्ठी विभक्ति होती है। जैसे-बालकः मातुः स्मरति। (बालक माता को स्मरण करता है।)
(यहाँ खेदपूर्वक स्मरण होने के कारण कर्म के स्थान पर षष्ठी हुई है।)

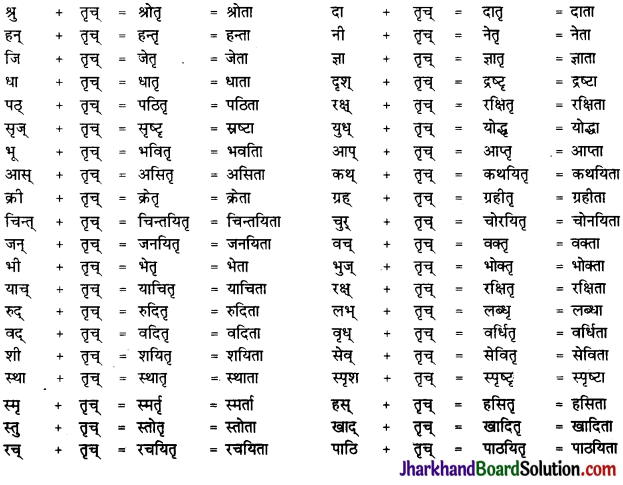
कर्तृकर्मणोः कृतिः – कृदन्त शब्द अर्थात् जिनके अन्त में कृत् प्रत्यय तृच् (तू), अच् (अ), घब् (अ), ल्युट् (अन्), क्तिन् (ति), ण्वुल (अक्) आदि रहते हैं। ऐसे शब्दों के कर्ता और कर्म में षष्ठी होती है।
यथा – (i) शिशोः रोदनम् (बच्चे का रोना।)
(ii) कालस्य गतिः। (समय की चाल।)

क्तस्य च वर्तमाने- भूतकाल का वाचक ‘क्त’ प्रत्ययान्त शब्द जब वर्तमान के अर्थ में प्रयुक्त होता है तब षष्ठी होती है। यथा-अहमेव मतो महीपतेः। (राजा मुझे ही मानते हैं।)

जासिनि प्रहणनाट क्राथपिषां हिंसायाम्-हिंसार्थक जस्, नि, तथा उपसर्गपूर्वक हन्, क्रथ, नट्, तथा पिस् धातुओं के कर्म में षष्ठी होती है। यथा – (i) बधिकस्य नाटयितुं क्राथयितुं वा (बधिक के वध करने के लिए।)
(ii) अपराधिनः निहन्तुं, प्रहन्तुं, प्राणिहन्तुं वा (अपराधी के मारने के लिए)

दिवस्तदर्थस्य-‘दिव्’ धातु का प्रयोग जुआ खेलने के अर्थ में होता है, तब उसके योग में भी कर्म में षष्ठी विभक्ति होती है। यथा – शतस्य दीव्यति। (सौ का जुआ खेलता है।)

अवयवावयविभाव होने पर अंशी तथा अवयवी में षष्ठी विभक्ति होती है।
यथा – (i) जलस्य बिन्दुः। (जल की बूंद।), (ii) रात्रेः पूर्वम्। (रात्रि के पूर्व।)

सप्तमी विभक्तिः

क्रियायाः सिद्धौ यः आधारः भवति तस्य अधिकरणसंज्ञा भवति (अधारोऽधिकरणम), अधिकरणे च (सप्तम्यधिकरणे च इति सूत्रेण) सप्तमी विभक्तिः भवति। यथा – (“आधारोऽधिकरणम्” क्रिया की सिद्धि में जो आधार होता है उसकी अधिकरण संज्ञा होती है और अधिकरण में ‘सप्तमभ्यधिकरणे च’ इस सूत्र से सप्तमी विभक्ति होती है। यथा –

1. नृपः सिंहासने तिष्ठति। (राजा सिंहासन पर बैठता है।)
2. वयं ग्रामे निवसामः। (हम गाँव में रहते हैं।)
3. तिलेषु तैलं विद्यते। (तिलों में तेल है।)

यस्मिन् स्नेहः क्रियते तस्मिन् सप्तमी विभक्तिः भवति। यथा – (जिस पर स्नेह किया जाता है उसमें सप्तमी विभक्ति होती है। जैसे-)

पिता पुत्रे स्निह्यति। (पिता पुत्र को प्रेम करता है।)

संलग्नार्थकशब्दानां चतुरार्थकशब्दानां च योगे सप्तमी विभक्तिः भवति। यथा – (संलग्नार्थक शब्दों तथा (युक्तः, व्याप्तः, तत्परः आदि) चतुरार्थक शब्दों (कुशलः, निपुणः, पटुः आदि) के साथ सप्तमी विभक्ति होती है। यथा-)
बलदेवः स्वकार्ये संलग्नः अस्ति। (बलदेव अपने कार्य में लगा है।)
जयदेवः संस्कृते चतुरः अस्ति। (जयदेव संस्कृत में चतुर है।)

यदा एकक्रियायाः अनन्तरं अपरा क्रिया भवति तदा पूर्वक्रियायाः तस्याश्च कर्तरि सप्तमी विभक्तिः भवति यस्य च
भावेन भावलक्षणम्)। यथा – (“यस्य च भावेन भावलक्षणम्” जब एक क्रिया के बाद दूसरी क्रिया होती है तब पूर्व क्रिया और उसके कर्ता में सप्तमी विभिक्ति होती है। जैसे-)

1. रामे वनं गते दशरथः प्राणान् अत्यजत्। (राम के वन जाने पर दशरथ ने प्राण त्याग दिए।)
2. सूर्ये अस्तं गते सर्वे बालकाः गृहम् अगच्छन्। (सूर्य अस्त होने पर सभी बालक घर गए।)

अन्य महत्त्वपूर्ण नियम –

‘साध्वसाधु प्रयोगे च’-अर्थात् साधु और असाधु शब्दों के प्रयोग करने पर सप्तमी विभक्ति होती है। जैसे –
कृष्ण: मातरि साधुः। (कृष्ण माता के प्रति अच्छा है।)

विषय में, बारे में तथा समयबोधक शब्दों में सप्तमी विभक्ति का प्रयोग होता है। जैसे –
(i) मम मोक्षे इच्छाऽस्ति।
(मेरी मोक्ष के विषय में इच्छा है।)
(ii) सः सायंकाले पठति।
(वह शाम को पढ़ता है।)

युज् धातु तथा उससे बनने वाले योग्य अथवा उपयुक्त आदि शब्दों के योग में सप्तमी विभक्ति होती है। जैसे –
(i) त्रैलोकस्य अपि प्रभुत्वं तस्मिन् युज्यते। (त्रैलोक्य का भी राज्य उसके लिए उचित है।)
(ii) स धर्माधिकारे नियुक्तोऽस्ति। (वह धर्माधिकार में लगाया गया है।)

‘अप’ उपसर्गपूर्वक राध् धातु और उससे बने हुए शब्दों के योग में, जिसके प्रति अपराध होता है, उसमें सप्तमी या . षष्ठी होती है। जैसे –
(i) सा पूजायोग्ये अपराद्धा। (उसने पूज्य व्यक्ति के प्रति अपराध किया है।)
(ii) सा पूजायोग्यस्य अपराद्धा। (उसने पूज्य के प्रति अपराध किया है।)
(ii) अपराद्धोऽस्मि तत्र भवतः कण्वस्य। (पूज्य कण्व के प्रति मैंने अपराध किया है।)

फेंकना या झपटना अर्थ की क्षिप, मुच् या अस् धातुओं के साथ सप्तमी विभक्ति आती है। जैसे –
(i) नृपः मृगे बाणं क्षिपति। (राजा हिरन पर बाण फेंकता है।)
(ii) मृगेषु बाणान् मुञ्चति। (मृगों पर बाण छोड़ता है।)

व्याप्त (संलग्न), तत्पर, व्यग्र, कुशल, निपुण, दक्ष, प्रवीण आदि शब्दों के योग में सप्तमी होती है। जैसे –
(i) जनाः गृहकर्मणि व्यापृताः सन्ति। (लोग गृहकार्य में संलग्न हैं।)
(ii) ते समाजसेवायां तत्पराः सन्ति। (वे समाज सेवा में लगे हुए हैं।)
(iii) मम पिता अध्यापने कुशलः, निपुणः दक्षः वा अस्ति। (मेरे पिता अध्यापन के कार्य में कुशल निपुण हैं।)

विशेष ध्यातव्य – पृथग्विनानानाभिस्तृतीयान्यतरस्याम् – पृथक्, बिना तथा नाना (बिना) के योग में द्वितीया, तृतीया तथा पंचमी में से किसी भी एक विभक्ति का प्रयोग हो सकता है।

प्रश्न 1.
अधोलिखित प्रश्नानां उत्तरस्य उचित विकल्पं चित्वा लिखत –
1. ‘अभितः’ शब्दस्य योगे विभक्तिः भवति –
(अ) चतुर्थी
(ब) पञ्चमी
(स) द्वितीया
(द) तृतीया
उत्तरम् :
(स) द्वितीया

2. ‘सह’ शब्दस्य योगे विभक्तिः भवति –
(अ) तृतीया
(ब) चतुर्थी
(स) पञ्चमी
(द) षष्ठी
उत्तरम् :
(अ) तृतीया

3. अङ्गविकारे विभक्तिः भवति –
(अ) प्रथमा
(ब) द्वितीया
(स) तृतीया
(द) सप्तमी
उत्तरम् :
(स) तृतीया

4. अधस्तनेषु चतुर्थी विभक्तेः कारणम् अस्ति –
(अ) नमः
(ब) सह
(स) अभितः
(द) प्रति
उत्तरम् :
(अ) नमः

5. अधस्तनेषु पंचमीविभक्तेः कारणम् अस्ति –
(अ) नमः
(ब) अनन्तरम्
(स) अधोऽधः
(द) खल्वाटः
उत्तरम् :
(ब) अनन्तरम्

6. अपादाने विभक्तिः भवति –
(अ) द्वितीया
(ब) तृतीया
(स) पञ्चमी
(द) षष्ठी
उत्तरम् :
(स) पञ्चमी

7. रक्षार्थकधातूनां योगे विभक्तिः भवति –
(अ) षष्ठी
(ब) सप्तमी
(स) पंचमी
(द) तृतीया
उत्तरम् :
(स) पंचमी

8. कारकाणां संख्या अस्ति –
(अ) सप्त
(ब) अष्ट
(स) षट्
(द) नव
उत्तरम् :
(स) षट्

9. सम्बोधने विभक्तिः भवति –
(अ) द्वितीया
(ब) प्रथमा
(स) तृतीया
(द) षष्ठी
उत्तरम् :
(ब) प्रथमा

10. …………… सह दीर्घकालीनानां युद्धानां कारणेन मेवाडराज्य स्थिति समीचीन नासीत् –
(अ) शत्रूणाम्
(ब) शत्रुभिः
(स) शत्रुभ्यः
(द) शत्रून्
उत्तरम् :
(ब) शत्रुभिः

11. सः …………….. निकषा गत्वा उवाच।
(अ) प्रतापम्
(ब) प्रतापस्य
(स) प्रतापेन
(द) प्रतापात्।
उत्तरम् :
(अ) प्रतापम्

12. तया सेनया च मुगलानां …………….. प्रति स्वातन्त्र्य युद्धं प्रारभत।
(अ) शासनस्य
(ब) शासनात्
(स) शासनम्
(द) शासनेन।
उत्तरम् :
(स) शासनम्

13. पितुः …………….. प्रागेव माता विपन्नाभवत्।
(अ) प्रयाणेन
(ब) प्रयाणस्य
(स) प्रयाणात्
(द) प्रयाणाय
उत्तरम् :
(स) प्रयाणात्

14. अरे धिक्……………..।
(अ) माम्
(ब) मम
(द) मयि।
उत्तरम् :
(अ) माम्

15. ……………. मल्लः सूरजमल्लः।
(अ) मल्लेषु
(ब) मल्लेभ्यः
(स) मल्ले:
(द) मल्लान्
उत्तरम् :
(अ) मल्लेषु

16. …………… सह सर्वेऽपि अनुचराः निःसरन्ति।
(अ) प्रतापस्य
(ब) प्रतापात्
(स) प्रतापाय
(द) प्रतापेन
उत्तरम् :
(द) प्रतापेन

17. रोचते ………….. एषः भद्र मयूरः।
(अ) मे
(ब) मम।
(स) माम्
(द) मयि।
उत्तरम् :
(अ) मे

18. एकस्य पशुचारकस्य …………… प्रति यात्रायाः प्रस्थान बिन्दुरासीत्।
(अ) महापुरुषत्वस्य
(ब) महापुरुषत्वम्
(स) महापुरुषत्वाय
(द) महापुरुषत्वे।
उत्तरम् :
(ब) महापुरुषत्वम्

प्रश्न 2.
कोष्ठकगतशब्देषु उचितविभक्तेः प्रयोगं कृत्वा रिक्तस्थानानि पूरयत।
1. नास्ति …………………. समः शत्रुः। (क्रोधः)
2. माता …………………. स्निहयति। (शिशु)
3. …………………. भीत: बालकः क्रन्दति। (चौर)
4. अलम् …………. (विवाद)
5. ……… ………. परितः जलम् अस्ति। (नदी)
6. …………………. रामायणं रोचते। (भक्त)
7. …………………. बहिः छात्राः कोलाहलं कुर्वन्ति। (कक्षा)
8. भिक्षुकः …………………. भिक्षां याचते। (नृप)
9. जनकः …………………. क्रुध्यति। (पुत्र)
उत्तराणि :
1. क्रोधस्य क्रोधेन वा
2. शिशौ
3. चौरात्
4. विवादेन
5. नदीम्
6. भक्ताय
7. कक्षायाः
8. नृपं
9. पुत्राय।

प्रश्न 3.
कोष्ठकेभ्यः शुद्धम् उत्तरं चित्वा रिक्तस्थानानि पूरयत –
1. …………………. सह सीता वनम् अगच्छत। (रामस्य/रामेण)
2. सुरेशः …………………. पुस्तकं यच्छति। (रामम्/रामाय)
3. …………………. नमः। (रामम्/रामाय)
4. माता …………………. क्रुध्यति। (पुत्र/पुत्राय)
5. पिता …………………. स्निह्यति। (पुत्रे/पुत्रात्)
6………………….. अभितः क्षेत्राणि सन्ति। (ग्रामस्य/ग्रामम्)
7. …………………. मोदकाः रोचन्ते। (बालकाय/बालकम्)
8. बालकः …………………. अधिशेते। (पर्यङ्के/पर्यङ्कम्)
उत्तराणि :
1. रामेण
2. रामाय
3. रामाय
4. पुत्राय
5. पुढे
6. ग्रामम्
7. बालकाय
8. पर्यङ्कम्।

प्रश्न 4.
कोष्ठाङ्कित पदे उचित विभक्तिं प्रयुज्य रिक्त स्थानं पूरयत –
(कोष्ठक में लिखे पद में उचित विभक्ति लगाकर रिक्त स्थान की पूर्ति कीजिए)
1. भवतु! अलम् …………….। (नाटक)
2. किं…………………… किञ्चिदपराद्धम् ? (भर्तृदारक)
3. रामदत्तोऽपि …………………. अनुसरति। (तद्)
4. रत्नापि ………………….. सार्धमायाति। (दारक)
5. ………………. अतितरां स्निह्यत्यसौ। (अस्मद्)
6. ………………. साकं युद्धं कृतवान्। (हम्मीरदेव)
7. सः …………………… आप …. अपि तीक्ष्णः। (पठन)
8. …………………… स्व पुस्तकं कस्मात् दत्तम् ?
9. सः ………………….. अपि रोचते। (अस्मद्)
10. …………………… साक …………… साकं मैत्रीवर्धनस्य न काप्यावश्यकता। (सोमधर)
11. अलं … (भिषगाह्वान्)
12. सहर्षं …………………… प्रति।। (रत्ना)
13. किं तस्य …………………… वा ? (जीवित)
14. पराक्रमं कुर्वाणः ………………… निःसृत्य युद्धरतोऽभवत्।
15. ………………….. अपि कमलं विकसति।
उत्तराणि :
1. नाटकेन
2. भर्तृदारकेण
3. तम्
4. दारकेण
5. मयि
6. हम्मीरदेवेन
7. पठने
8. तस्मै
9. मह्यम्
10. सोमधरेण
11. भिषगाह्वानेन
12. रत्नाम्
13. जीवितेन
14. दुर्गात्
15. पङ्के।

प्रश्न 5.
समुचितविभक्तिपदेन वार्तालापं पूरयत – (उचित विभक्ति पदों से वार्तालाप को पूर्ण कीजिए-)
मोहन: – त्वं कस्मिन् विद्यालये पठसि?
हरीश: – अहं नवोदयविद्यालये पठामि।
मोहनः – तव विद्यालयः कीदृशः अस्ति?
हरीश: – मे …………
(i) (विद्यालय) परितः वनानि सन्ति।
मोहन: – त्वं विद्यालयं कदा गच्छसि?
हरीश: – अहं विद्यालयं दशवादने गच्छामि।
मोहन: – तव मित्र महेशः तु खञ्जः अस्ति।
हरीश:- आम् सः………..(ii) (दण्ड) चलति।
मोहनः – हरीश! तव माता प्रात:काले कुत्र गच्छति?
हरीश: – मम माता प्रात:काले………….. (iii) (भ्रमण) गच्छति।
मोहन: – अतिशोभनम्………….. (iv) (स्वास्थ्यलाभ) मा प्रमदितव्यम्।
सहसा शिक्षकः कक्षे प्रवेशं करोति वदति च अलम्…………. (v) (वार्तालाप)।
उत्तरम् :
(i) विद्यालयं
(ii) दण्डेन
(iii) भ्रमणाय
(iv) स्वास्थ्यलाभात्
(v) वार्तालापेण।

प्रश्न 6.
कोष्ठके प्रदत्तशब्दानां समुचितविभक्तिपदैः अधोलिखितं वार्तालापं पूरयत। (कोष्ठक में दिये गये शब्दों की उचित विभक्ति पदों से निम्नलिखित वार्तालाप को पूर्ण कीजिए-)
कमला – महेश! किं त्वमपि (i) …………..(विद्यालय) प्रति गच्छसि?
महेशः – आम् (ii) ……………..(युष्मद्) सह कः गच्छति?
कमला – मम कक्षायाः सहपाठिनः आगच्छन्ति।
महेश: – शिक्षकः अपि अधुना गच्छति।
छात्रा: – (iii) ………….(शिक्षक) नमः।
शिक्षकः – नमस्ते। प्रसन्नाः भवन्तु। (iv) ………………(ग्राम) बहिः क्रीडास्थलं गच्छन्ति भवन्तः?
छात्राः – (v) ………(विद्यालय) पुरतः क्रीडास्थले वयं क्रीडामः।
उत्तरम् :
(i) विद्यालयं
(ii) त्वया
(iii) शिक्षकाय
(iv) ग्रामात्
(v) विद्यालयस्य।

प्रश्न 7.
कोष्ठकगतपदेषु चितविभक्तिं प्रयुज्य वाक्यानि पूरयत –
(कोष्ठक में दिये पदों में उचित विभक्ति प्रयुक्त कर वाक्यों को पूर्ण कीजिए)
(क) पुरा (i) …………..(हस्तिनापुर) शान्तनुः नाम नृपतिः अभवत्। देवव्रतः (ii) …………….(शान्तनु) गंगायाः च पुत्रः आसीत्। एकदा शान्तुनः (iii) …………..(यमुना) तीरे सत्यवतीम् अपश्यत्। यदा देवव्रतः इदं सर्व (iv) ……….(वृत्तान्त) अवागच्छत् स धीवरस्य गृहम् अगच्छत्। धीवरः सत्यवत्याः विवाहं (v) ………… (नृपति) सह अकरोत्।
उत्तरम् :
(i) हस्तिनापुरे
(ii) शान्तनोः
(iii) यमुनायाः
(iv) वृत्तान्तम्
(v) नृपतिना।

(ख) तत्र (i) …………….(ग्राम) निकषा एकः देवालयः अस्ति। देवालये बहवः जनाः आगच्छन्ति परं कोऽपि
(ii) ………(पुत्र) हीनः नास्ति।
(iii) …………..(देवालय) बहिः एक सरोवरः अस्ति। सरोवरे विकसितानि कमलानि।
(iv) ……….. (दर्शक) रोचन्ते।
(v) ………..(सरोवर) तटे एकः उद्यानम् अपि अस्ति।
उत्तरम् :
(i) ग्रामं
(ii) पुत्रैः
(iii) देवालयात्
(iv) दर्शकेभ्यः
(v) सरोवरस्य।

प्रश्न 8.
कोष्ठान्तर्गतशब्देषु उचितां विभक्तिं प्रयुज्य वाक्यानि पूरयत –
(कोष्ठक में दिये शब्दों में उचित विभक्ति प्रयुक्त कर वाक्यों को पूर्ण कीजिए-)
(i) ……………अभितः नद्यौ स्तः (ग्राम)
(ii) …………मोदकं रोचते। (बालक)
(ii) धिक्…………ये वेदान् न पठन्ति। (ब्राह्मण)
(iv) ………..योगेशः पटुः। (बालक)
उत्तरम् :
(i) ग्रामम्
(ii) बालकाय
(iii) ब्राह्मणान्
(iv) बालकेषु।

प्रश्न 9.
कोष्ठकात् उचितं पदं चित्वा रिक्तस्थानानि पूरयत – (कोष्ठक से उचित पद चुनकर रिक्तस्थानों की पूर्ति कीजिए-)
(i) ………….विना जीवनं नास्ति। (जलम्/जलस्य)
(ii) …………. भक्तिः रोचते। (हरये/हरिः)
(iii) रामः………….जुगुप्सते। (पापेन/पापात्)
(iv) सः ……………गार्योऽस्ति। (गोत्रेण/गोत्रस्य)
(v) ईश्वरः………….वर्तते। (सर्वे/सर्वस्मिन्)
उत्तरम् :
(i) जलम्
(ii) हरये
(iii) पापात्
(iv) गोत्रेण
(v) सर्वस्मिन्।

प्रश्न 10.
क खण्डं ख खण्डेन सह योजयत।
‘क खण्डः’ – ‘ख खण्डः’
1. दा धातुयोगे – 1. षष्ठी
2. रुच् धातुयोगे – 2. तृतीया
3. अङ्गविकारे – 3. चतुर्थी
4. सम्बन्धे – 4. चतुर्थी
5. अधितिष्ठति योगे – 5. सप्तमी
6. श्रद्धायोगे – 6. द्वितीया
7. प्रमाद्यति धातुयोगे – 7. प्रथमा
8. कर्मवाच्यस्य कर्मणि – 8. पञ्चमी
उत्तराणि :
‘क खण्डः’ – ‘ख खण्डः’
1. दा धातुयोगे – 1. चतुर्थी
2. रुच् धातुयोगे – 2. चतुर्थी
3. अङ्गविकारे – 3. तृतीया
4. सम्बन्धे – षष्ठी
5. अधितिष्ठतियोगे – 5. द्वितीया
6. श्रद्धायोगे – 6. सप्तमी
7. प्रमाद्यति धातुयोगे – 7. पञ्चमी
8. कर्मवाच्यस्य कर्मणि – 8. प्रथमा

प्रश्न 11.
अधोलिखितशब्दानां योगे चितविभक्तिप्रयोगं कृत्वा वाक्यरचनां कुरुत।
1. विना …………….
2. धिक् …………….
3. बहिः …………….
4. विभेति …………….
5. काणः …………….
6. अन्तरा …………
7. पटुतरः …………….
8.. पटुतमः …………….
9. स्वाहा …………….
10. उपवसति …………….
11. अधः …………….
12. कुशलः …………….
उत्तराणि :
1. प्रदीपः पुस्तकं विना पठति।
2. धिक् मूर्खम्
3. ग्रामात् बहिः मन्दिरम् अस्ति।
4. बालकः चौरात् विभेति।
5. सः नेत्रेण काणः अस्ति।
6. सः भोजनम् अन्तरेण जीवति।
7. रामः श्यामात् पटुतरः अस्ति।
8. छात्राणां छात्रेषु वा मोहनः पटुतमः अस्ति।
9. इन्द्राया स्वाहा।
10. श्यामः नगरम् उपवसति।
10. वृक्षस्य अधः सर्पः अस्ति।
11. शिक्षकेषु मुरारी लालः कुशलः।

प्रश्न 12.
अधोलिखितपदानां वाक्येषु प्रयोगं कुरुत – (निम्नलिखित शब्दों का संस्कृत वाक्यों में प्रयोग कीजिए-)
प्रति, उद्घाटितम, सह, करणीया, अलम, बहिः, कर्तव्यः, साकम्, किम्, नीता, मग्नः, जायते, सम्भवति, अन्तरेण, याचते।
उत्तरम् :

1. प्रति – श्रृगालः ग्राम प्रति धावति। (गीदड़ गाँव की ओर दौड़ता है।)
2. उद्घाटितम् – अद्य त्वया मम नेत्रयुगलम् उद्घाटितम्। (आज तुमने मेरी आँखें खोल दी।)
3. सह – रामेण सह सीतापि वनमगच्छत्। (राम के साथ सीता भी वन को गई।)
4. करणीया – सज्जापि मया एव करणीया। (सजावट भी मुझे ही करनी है।)
5. अलम् – अलं विवादेन। (विवाद मत करो।)
6. वहिः – सः दुर्गाद् बहिरागच्छत्। (वह दुर्ग से बाहर आ गया।)
7. कर्त्तव्यः – मया एव सर्वप्रथम खड्गप्रहारः कर्त्तव्यः। (मुझे ही सबसे पहले तलवार का प्रहार करना चाहिए।)
8. साकम् – दुर्गद्वारमागत्य हम्मीरदेवेन साकं युद्धं कृतवान्। (दुर्ग के द्वार पर आकर हम्मीरदेव के साथ युद्ध किया।)
9. किम् – किम् मम एतया मृत्तिका शकटिकया ? (मुझे इस मिट्टी की गाड़ी से क्या प्रयोजन ?)
10. नीता- तेन श्रेष्ठिपुत्रेण सा स्वर्णशकटिका नीता। (वह श्रेष्ठ का बेटा उस सोने की गाड़ी को ले गया।)
11. मग्न: – सः ध्याने मग्नः मां नापश्यत्। (ध्यान में डूबे हुए उसने मुझे नहीं देखा।)
12. जायते – जलात् जायते जलजः। (कमल पानी से पैदा होता है।)
13. सम्भवति – अन्नं पर्जन्यात् सम्भवति। (अन्न वृष्टि से होता है।)
14. अन्तरेण – न सुखं धनमन्तरेण। (धन के बिना सुख नहीं।)
15. याचते – रामदत्तः माम् पुस्तकं याचते। (रामदत्त मुझसे पुस्तक माँगता है।)

प्रश्न 13.
अधस्तनेषु स्थूलशब्देषु विभक्तेः कारणं लिखत –

1. ग्रामं परितः क्षेत्राणि सन्ति।
2. कविषु कालिदासः श्रेष्ठः।
3. हरये रोचते भक्तिः।
4. हरिः वैकुण्ठम् अधिशेते।
5. कृषक: ग्रामम् अजां नयति।
6. साधुः कर्णाभ्यां बधिरः अस्ति।
7. हिमालयात् गंगा प्रभवति।
8. रामः श्यामाय शतं धारयति।
9. हनुमते नमः

उत्तराणि :

1. ‘परितः”योगे द्वितीया विभक्तिः भवति (परितः के योग में द्वितीया विभक्ति होती है।)
2. ‘इष्टन्’ अथवा ‘तमप्’ प्रत्ययस्य योगे यस्मात् च विशेषता प्रदर्शयते तस्मिन् षष्ठी विभक्तेः अथवा सप्तमी विभक्ते प्रयोगः भवति। (‘इष्ठन् ‘ अथवा ‘तमप्’ प्रत्यय के योग में जिससे विशेषता प्रदर्शित की जाती है उसमें षष्ठी विभक्ति का अथवा सप्तमी विभक्ति का प्रयोग होता है।)
3. रुच्यर्थानां प्रीयमाणः अर्थात् रुच्यर्थानां धातूनां योगे चतुर्थी विभक्तिः भवति। (‘रुच’ अर्थ वाली धातुओं के योग में चतुर्थी विभक्ति होती है।)
4. अधि-उपसर्गपूर्वक शीङ् धातोः योगे द्वितीया विभक्ति भवति। (‘अधि’ उपसर्गपूर्वक ‘शीङ्’ धातु के योग में द्वितीया विभक्ति होती है।)
5. ‘नी’ धातोः योगे द्वितीया विभक्ति भवति। (‘नी’ (हो जाना) धातु के योग में द्वितीया विभक्ति होती है।
6. “येनाङ्ग विकारः” विकृताङ्गे तृतीया विभक्तिः भवति। (“येनाङ्ग विकारः” सूत्र से विकृत अङ्ग में तृतीया विभक्ति होती है।)
7. ‘भुवः प्रभाव:’ सूत्रेण उत्पत्तिस्थाने पञ्चमी विभक्तिः भवति। (‘भुवः प्रभावः’ सूत्र से उत्पत्ति स्थान में पञ्चमी विभक्ति होती है।)
8. धृञ् धातो: योगे उत्तमर्णे (ऋणदाता) चतुर्थी विभक्ति भवति। (धृञ् धातु के योग में उत्तमर्ण में (ऋणदाता में) चतुर्थी विभक्ति होती है।)
9. नमः योगे चतुर्थी विभक्तिः भवति। (नमः के योग में चतुर्थी विभक्ति होती है।)

प्रश्न 14.
रेखाङ्कित पदेषु विभक्ति निर्देशं कृत्वा कारण लिखत – (रेखांकित शब्दों में विभक्ति बताते हुए कारण बताइये।)
1. महत्सु श्रङगेषु महीधराणां विश्रम्य प्रयाति
उत्तरम् :
सप्तमी बहुवचनम्। अधिकरणे सप्तमी।

2. स्वेषाम् अपत्यानाम् उपरि सौहार्दत्वात् अनुग्रहं चकारः।
उत्तरम् :
षष्ठी-बहुवचनम् उपरि शब्दस्य योगे षष्ठी विभक्ति।

3. अनुकृतम् अनेन पितुः रूपम्।
उत्तरम् :
तृतीयाः एकवचनम्। कर्मवाच्यकर्तरि तृतीया।

4. मया इयं मृत्तिकाशकटिका दत्ता।
उत्तरम् :
तृतीया-एकवचनम्। कर्मवाच्ये कर्तरि तृतीयाः

5. धिङ् मुर्खान्।
उत्तरम् :
द्वितीया-बहवचनम। धिक योगे द्वितीया।

6. मुग्धेन मुखेन अति करुणं मन्यमसि।
उत्तरम् :
तृतीया एकवचनम्। करणे तृतीया।

7. हम्मीरदेवेन साकं युद्धं कृतवान्।
उत्तरम् :
तृतीया-एकवचनम्। सहयुक्तेऽप्रधाने तृतीया।

8. हम्मीरदेवं प्रति दूतः प्रहितः।
उत्तरम् :
द्वितीया-एकवचनम्। ‘प्रति’ योगे द्वितीया।

9. महिमासाहिना सह त्वामन्तकपुरं नेष्यामि।
उत्तरम् :
तृतीया-एकवचनम्। सहयुक्तेऽप्रधाने तृतीया।

10. सर्वे दुर्गादबहिः स्थानान्तरं गच्छत।
उत्तरम् :
पञ्चमी-एकवचनम्। बहियोगे पंचमी।।

11. अधिवक्तुः पटनी रला अपि दारकेण सार्धम् आयाति।
उत्तरम् :
तृतीया-एकवचनम्। सहयुक्तेऽप्रधाने तृतीया।

12. सोमधरः मम सुहृदस्ति।
उत्तरम् :
षष्ठी एकवचनम्। सम्बन्धे षष्ठी।।

13. सोमघरेण साकं मैत्री वर्धनस्य न काप्यावश्यकता।
उत्तरम् :
तृतीया-एकवचनम्। सहयुक्तेऽप्रधाने तृतीया।

14. त्वया सख्यमेव कस्मात् कृतम्।
उत्तरम् :
तृतीया-एकवचनम्। कर्मवाच्ये कर्तरि तृतीया।

प्रश्न 15.
रेखाङ्कित पदेषु विभक्ति निर्देशं कृत्वा कारण लिखत –
1. (i) सः लगडेन चलन्तं वृद्धम् अपश्यत्।
(i) अहम् एनं हंसम् अहनम्।
2. (i) अहं शरणार्थिनं कदापि व्याधाय न दास्यामि।
(ii) सिद्धार्थः प्रासादात. वनं निरगच्छत्।
3. (i) गंगा शान्तनोः भार्या आसीत्।
(ii) स्वां रूपवती दुहितरं मह्यं यच्छ।
4. (i) अहं सदा ब्रह्मचर्येण स्थास्यामि।
(ii) मम पित्रे स्वां दुहितरं यच्छ।
5. (i) अहं सत्यवतीं तभ्यं विवाहे. दास्यामि।
(ii) नूपतिना सह विवाहमकरोत्।
6. (i) सर्वे भूम्या सह पुत्रवत् समाचरन्तु।
(ii) प्रशासका: गुप्तसंदेशाय कपोतानाम् उपयोगम् अकुर्वन्।
7. (i) जनाः विद्यत तरंगैः संदेशं प्रेषयन्ति स्म।
(ii) सांस्कृतिक-विकासे वनानां भूमिकास्ति।
8. (i) वनानां सम्बन्धोऽपि मानवेन सह विद्यते।
(ii) सिंहः दुर्गायाः वाहनमस्ति।
9. (i) सर्वे पशुपक्षिणो देवताभिः सह सम्बद्धाः सन्ति।
(ii) पुत्रस्य नेत्राभ्याम् अश्रुधारा प्रवहति स्म।
10. (i) सः पितः चरणयोः अपतत्।
(ii) समाजे नार्याः महत्वपूर्ण स्थानं वर्तते।
11. (i) स्त्रियोऽपि पुरुषैः समं विभिन्नेषु क्षेत्रेषु प्रगतिं कुर्युः।
(ii) स राज्यकार्य विहाय समाजसेवायां प्रवृत्तोऽभवत्।
12. (i) माता पुत्रान् पोषयति।
(ii) धेनुभिः सह मातृतुलना कृता।
13. (i) सः सिंहशावकेन सह क्रीडति स्म।
(ii) गंगा-यमुना-प्रभृतयः नद्यः हिमालयात प्रभवन्ति।
14. (i) वृक्षेभ्यः नानाविधानि फलानि पुष्पाणि च उत्पद्यन्ते।
(ii) युद्धेन किं प्रयोजनम्?
15. (i) चौराद् बिभेति।
(ii) सः दण्डेन सर्प ताडितवान्।
16. (i) मेदपाटस्य महिमा देशरक्षायै विशिष्टरूपेण उल्लेखनीया।
(ii) प्रतापात भीताः शत्रवः मेदपाटं न आयाताः।
17. (i) संग्रामसिंहः युद्धे शत्रुभ्यः अक्रुध्यत्।
(ii) सः युद्धक्षेत्रे अक्ष्णा काणः अभवत्।
18. (i) सः पादेन खञ्जः।
(ii) सः पर्यकम् अधिशेते।
19. (i) सः आसन्दिकाम् अध्यास्ते।
(ii) नमः शिवाय।
20. (i) सः हस्तेन लुञ्जः अभवत्।
(ii) पिता पुत्राय क्रुध्यति।
उत्तराणि :
1. (i) करण कारके तृतीया विभक्तिः भवति।
(ii) कर्मणि द्वितीया विभक्तिः भवति।

2. (i) सम्प्रदाने चतुर्थी विभक्तिः भवति।
(ii) अपादाने पञ्चमी विभक्तिः भवति।

3. (i) सम्बन्धे षष्ठी विभक्तिः भवति।
(ii) सम्प्रदाने चतुर्थी विभक्तिः भवति।

4. (i) करण कारके तृतीया विभक्तिः भवति।
(ii) सम्प्रदाने चतुर्थी विभक्तिः भवति।

5. (i) सम्प्रदाने चतुर्थी विभक्तिः भवति।
(ii) ‘सह’ योगे तृतीया विभक्तिः भवति।

6. (i) ‘सह’ योगे तृतीया विभक्तिः भवति।
(ii) सम्प्रदाने चतुर्थी विभक्तिः भवति।

7. (i) करण कारके तृतीय विभक्तिः भवति।
(ii) अधिकरणे सप्तमी विभक्तिः भवति।

8. (i) ‘सह’ योगे तृतीया विभक्तिः भवति।
(ii) सम्बन्धे षष्ठी विभक्तिः भवति।।

9. (i) ‘सह’ योगे तृतीया विभक्तिः भवति।
(ii) अपादाने पञ्चमी विभक्तिः भवति।

10. (i) सम्बन्धे षष्ठी विभक्तिः भवति।
(ii) अधिकरणे सप्तमी विभक्तिः भवति।

11. (i) ‘समम्’ योगे द्वितीया विभक्तिः भवति।
(ii) कर्मणि द्वितया विभक्तिः भवति।

12. (i) कर्मणि द्वितीया विभक्तिः भवति।
(ii) ‘सह’ योगे तृतीया विभक्तिः भवति।

13. (i) ‘सह’ योगे तृतीया विभक्तिः भवति।
(ii) उत्पत्ति स्थाने पञ्चमी विभक्तिः भवति।

14. (i) उत्पत्ति स्थाने पञ्चमी विभक्तिः भवति।
(ii) ‘प्रयोजन’ योगे तृतीया विभक्तिः भवति।

15. (i) ‘भी’ धातोः योगे पञ्चमी विभक्तिः भवति।
(ii) करण कारके तृतीया विभक्तिः भवति।

16. (i) सम्प्रदाने चतुर्थी विभक्तिः भवति।
(ii) ‘भी’ धातोः योगे पञ्चमी विभक्तिः भवति।

17. (i) ‘कृध्’ धातोः योगे चतुर्थी विभक्तिः भवति।
(ii) येनाङ्ग विकारे तृतीया विभक्तिः भवति।

18. (i) येनाङ्ग विकारे तृतीया विभक्तिः भवति।
(ii) अधि + शी धातोः योगे द्वितीया विभक्तिः भवति।

19. (i) अधि + आस् धातोः योगे द्वितीया विभक्तिः भवति।
(ii) नमः धातोः योगे चतुर्थी विभक्तिः भवति।

20. (i) येनाङ्ग विकारे तृतीया विभक्तिः भवति।।
(i) ‘क्रुध्’ धातोः योगे चतुर्थी विभक्तिः भवति।

प्रश्न 16.
अधोलिखितवाक्यानि संशोधनीयानि –
1. राजपुरुषः चौरस्य अनुधावति।
2. ग्रामस्य परितः जलम् अस्ति।
3. साधुः दुर्जनेन जुगुप्सते।
4. अहं रेलयानात् ग्रामं गमिष्यामि।
उत्तरम् :
1. राजपुरुषः चौरम् अनुधावति।
2. ग्रामम् परितः जलम् अस्ति।
3. साधुः दुर्जनात् जुगुप्सते।
4. अहं रेलयानेन ग्रामं गमिष्यामि।

प्रश्न 17.
अधोलिखितवाक्यानि संशोधनीयानि –
1. ईश्वरं नमः।
2. अध्यापकः आसनम् तिष्ठति।
3. मह्यं मिष्टान्नं रोचते।
4. अलं विवादम्।
उत्तरम् :
1. ईश्वराय नमः।
2. अध्यापकः आसने तिष्ठति।
3. माम् मिष्टान्नं रोचते।
4. अलं विवादेन।

प्रश्न 18.
अधोलिखितवाक्यानि संशोधनीयानि –
1. विद्यालयम् अभितः वाटिका।
2. ग्रामस्य परितः जलम् अस्ति।
3. श्रमस्य विना फलं न मिलति।
4. अहं रेलयांनात् ग्रामं गमिष्यामि।
उत्तरम् :
1. विद्यालस्य अभितः वाटिका।
2. ग्रामं परितः जलम् अस्ति।
3. श्रमात, श्रम, श्रमेण वा विना फलं न मिलति।
4. अहं रेलयानेन ग्रामं गमिष्यामि।

प्रश्न 19.
अधोलिखितवाक्यानि संशोधनीयानि –
1. महावीरं नमः।
2. हरिः मथुरायाम् अधितिष्ठिति।
3. शिवः पार्वत्याः सह तिष्ठति।
4. अलं विवादम्।
उत्तरम् :
1. महावीराय नमः
2. हरिः मथुराम् अधितिष्ठति
3. शिवः पार्वत्या सह तिष्ठति
4. अलं विवादेन।

प्रश्न 20.
अधोलिखितवाक्यानि संशोधनीयानि
1. व्याघ्रः मृगेषु हन्ति।
2. सिंहः शावका: व्यांपादयति।
3. अहं तुभ्यं न पश्यामि।
4. स: गुरवे प्रणमति।
5. ग्रामस्य परितः जलम् अस्ति।
उत्तरम् :
1. व्याघ्रः मृगान् हन्ति।
2. सिंहः शावकान् व्यापादयति।
3. अहं त्वाम् न पश्यामि।
4. स: गुरुं प्रणमति।
5. ग्रामं परितः जलम् अस्ति।

प्रश्न 21.
अधोलिखितवाक्यानि संशोधनीयानि –
1. रामः शरात् रावणं हन्ति।
2. आवां कन्दुकात् क्रीडामः।
3. रामः ग्रन्थः पठ्यते।
4. सः स्वपितुः सह आपणं गच्छति।
5. शिक्षकः पादात् खञ्जः।।
उत्तरम् :
1. रामः शरेण रावणं हन्ति।
2. आवां कन्दुकेन क्रीडामः।
3. रामेण ग्रन्थः पठ्यते।
4. सः स्व पित्रा सह आपणं गच्छति।
5. शिक्षकः पादेन खञ्जः।

प्रश्न 22.
अधोलिखितवाक्यानि संशोधनीयानि –
1. सः पुष्पान् स्पृहयति।
2. धनिकः निर्धनं भोजनं ददाति।
3. नृपः विप्रान् धनं वितरति।
4. माम् मोदकं रोचते।
5. कः मित्रं द्रुह्यति।
उत्तरम् :
1. सः पुष्पेभ्यः स्पृहयति।
2. धनिकः निर्धनाय भोजनं ददाति।
3. नृपः विप्रेभ्यः धनं वितरति।
4. मह्यं मोदकं रोचते।
5. कः मित्राय द्रुह्यति ?

प्रश्न 23.
अधोलिखितवाक्यानि संशोधनीयानि –
1. मानवः सिंहेन बिभेति।
2. सुमित्रं पापेन निवारयति।
3. शिष्यः आचार्येण बिभेति।
4. ग्रामस्य बहिर् एकम् उद्यानम्।
5. ब्रह्मणा प्रजाः प्रजायन्ते।
उत्तरम् :
1. मानवः सिंहात् बिभेति।
2. सुमित्रं पापात् निवारयति।
3. शिष्यः आचार्यात् बिभेति।
4. ग्रामात् बहिर् एकम् उद्यानम्।
5. ब्रह्मणः प्रजाः प्रजायन्ते।

प्रश्न 24.
अधोलिखितवाक्यानि संशोधनीयानि
1. बालक: मातरम् स्मरति।
2. अर्जुनः पाण्डुना पुत्रः आसीत्।
3. देवदत्तः अन्नाय हेतोः वसति।
4. सर्वैः पित्रा आज्ञा पालनीया।
उत्तरम् :
1. बालकः मातुः स्मरति।
2. अर्जुनः पाण्डोः पुत्रः आसीत्।
3. देवदत्तः अन्नस्य हेतोः वसति।
4. सर्वैः पितुः आज्ञा पालनीया।

प्रश्न 25.
अधोलिखितवाक्यानि संशोधनीयानि
1. सः मया वैरं विदधाति।
2. बालकः कार्यस्य कुशलः अस्ति।
3. शिष्यः अध्ययनेन रतः।
4. सूर्यस्य अस्तंगते छात्राः गृहम् आगच्छन्।
5. शिष्यः गुरोः भक्तिं करोति।
उत्तरम् :
1. स: मयि वैरं विदधाति।
2. बालकः कार्ये कुशलः अस्ति।
3. शिष्यः अध्ययने रतः।
4. सूर्ये अस्तंगते छात्राः गृहम् आगच्छन्।
5. शिष्यः गुरौ भक्तिं करोति।

प्रश्न 26.
अधोलिखित कारकाणां लक्षणानि उदाहरणानि च लिखत।
(नीचे लिखे कारकों के लक्षण और उदाहरण लिखिए।)
(क) करणम्
(ख) सम्प्रदानम्
(ग) अपादानम्
(घ) अधिकरणम्।
उत्तरम् :
(क) करणम् – (i) साधकतमं करणम् (ii) कर्तृकरणयो स्तृतीया-गोपाल: जलेन मुखं प्रक्षालयति।
(ख) सम्प्रदानम् – (i) कर्मणा यमभिप्रेति स सम्प्रदानम् (ii) चतुर्थी सम्प्रदाने-ब्राह्मणाय गां ददाति।
(ग) अपादानम् – (i) ध्रुवमपायेऽपादानम् (ii) अपादान पञ्चमी-वृक्षात् पत्राणि पतन्ति।
(घ) अधिकरणम् – (i) आधारोऽधिकरणम् (ii) सप्तम्यधिकरणे च-आसने उपविशति।

प्रश्न 27.
कारकस्य परिभाषा लेखनीया। (कारक की परिभाषा लिखिए।)
उत्तरम् :
‘क्रियाजनकत्वं कारकम अथवा क्रियां करोति निवर्तयति इति कारकम’ अतः यः क्रियां सम्पादयति अथवा यस्य क्रियया सह साक्षात् परम्परया वा सम्बन्धो भवति सः कारक इति कथ्यते।

प्रश्न 28.
संस्कृते कति कारकाणि सन्ति? तेषां नामानि लिखत। (संस्कृत में कितने कारक हैं? उनके नाम लिखिए।)
उत्तरम् :
संस्कृते षट् कारकाणि सन्ति-कर्ता, कर्म, करणम्, सम्प्रदानम्, अपादानम्, अधिकरणम् च। सम्बोधने प्रथमा विभक्तिः एव भवति, अतः अस्य परिगणनं प्रथमायामेव भवति। सम्बन्धस्य परिगणना कारकान्तर्गते न भवति।

प्रश्न 29.
अधोलिखितशब्देषु उचितविभक्तिप्रयोगं कृत्वा वाक्यरचनां कुरुत।
(निम्नलिखित शब्दों में उचित बिभक्ति का प्रयोग करके वाक्य बनाइए-)
1. विना ………….
2. धिक ………….
3. बहिः ………….
4. बिभेति ………….
5. काणः ………….
6. अन्तरा ………….
उत्तराणि :
1. विना – ज्ञानं विना न सुखम्
2. धिक् – धिक मूर्खम
3. बहिः – नगरात्बहिः उपवनम् अस्ति।
4. बिभेति – बालकः चौरात् बिभेति
5. काण: – नेत्रेण काण:
6. अन्तर – रामम् अन्तरा न गतिः।

प्रश्न 30.
अधोलिखितशब्देषु उचितविभक्तिप्रयोगं कृत्वा वाक्यरचनां कुरुत।
1. पटुतरः ………….
2. पटुतमः ………….
3. स्वाहा ………….
4. उपवसति ………….
5. अधः ………….
6. कुशलः ………….
उत्तराणि :
1. पटुतर: – राम कृष्णात् पटुतरः
2. पटुतमः – कवीनां कविषु वा कालिदासः पटुतमः
3. स्वाहा – इन्द्राय स्वाहा
4. उपवसति – हरिः वैकुण्ठम् उपवसति।
5. अध: – वृक्षस्य अधः कृष्णसर्पः निवसतिस्म।
6. कुशल – मम पिता अध्यापने कुशलः।

Jharkhand Board JAC Class 10 Sanskrit Solutions Shemushi Chapter 11 प्राणेभ्योऽपि प्रियः सुहृद् Textbook Exercise Questions and Answers.

JAC Board Class 10th Sanskrit Solutions Shemushi Chapter 11 प्राणेभ्योऽपि प्रियः सुहृद्

JAC Class 10th Sanskrit प्राणेभ्योऽपि प्रियः सुहृद् Textbook Questions and Answers

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखिये)
(क) कः चन्दन दासं दृष्टुम् इच्छति?
(चन्दनदास से कौन मिलना चाहता है?)
उत्तरम् :
चाणक्यः।

(ख) चन्दनदासस्य वणिज्या कीदृशी आसीत्?
(चन्दनदास का व्यापार कैसा था?)
उत्तरम् :
अखण्डिता (बाधा रहित)।

(ग) किं दोषम् उत्पादयति?
(क्या दोष पैदा करता है?)
उत्तरम् :
गृहजन प्रच्छादनम्। (घरवालों को छुपाना)।

(घ) चाणक्य के द्रष्टुम् इच्छति?
(चाणक्य किससे मिलना चाहता है?)
उत्तरम् :
चन्दनदासम् (चन्दन दास का)।

(ङ) कः शङ्कनीयः भवति ?
(कौन शंका के योग्य होता है?)
उत्तरम् :
अत्यादरः (अधिक आदर)।

प्रश्न 2.
अधोलिखितप्रश्नानाम् उत्तराणि संस्कृतभाषया लिखत –
(निम्नलिखित प्रश्नों के उत्तर संस्कृत भाषा में लिखिए)
(क) चन्दनदासः कस्य गहजनं स्वगृहे रक्षति स्म ?
(चन्दनदास किसके परिवारवालों को अपने घर में रखता था ?)
उत्तरम् :
चन्दनदासः अमात्यराक्षसस्य गृहजनं स्वगृहे रक्षति स्म।
(चन्दनदास अमात्य राक्षस के परिवार के लोगों को अपने घर में रखता था।)

(ख) तृणानां केन सह विरोधः अस्ति ?
(तिनको का किसके साथ विरोध है ?)
उत्तरम् :
तृणानाम् अग्निना सह विरोधः अस्ति।
(तिनकों का अग्नि के साथ विरोध है।)

(ग) पाठेऽस्मिन् चन्दनदासस्य तुलना केन सह कृता ?
(इस पाठ में चन्दनदास की तुलना किसके साथ की गई है?)
उत्तरम् :
पाठेऽस्मिन् चन्दनदासस्य तुलना शिविना सह कृता।
(इस पाठ में चन्दनदास की तुलना शिवि के साथ की गई है।)

(घ) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियं के इच्छन्ति ?
(कौन (लोग) प्रसन्नस्वभाव वालों से उपकार का बदला चाहते हैं ?)
उत्तरम् :
प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियं राजानः इच्छन्ति। (राजा (लोग) प्रसन्न स्वभाव वालों से उपकार का बदला चाहते

(ङ) कस्य प्रसादेन चन्दनदासस्य वणिज्या अखण्डिता ? (किसकी कृपा से चन्दनदास का व्यापार निर्बाध था ?)
उत्तरम् :
आर्यचाणक्यस्य प्रसादेन चन्दनदासस्य वणिज्या अखण्डिता।
(आर्य चाणक्य की कृपा से चन्दनदास का व्यापार निर्बाध था।)

प्रश्न 3.
स्थूलाक्षरपदानि आधृत्य प्रश्ननिर्माणं कुरुत –
(मोटे छपे शब्दों के आधार पर प्रश्न-निर्माण कीजिए)
(क) शिविना विना इदं दुष्करं कार्यं कः कुर्यात्
(शिवि के बिना यह दुष्कर कर्म कौन करे।)
उत्तरम् : केन विना इदं दुष्करं कार्य कः कुर्यात् ?
(किसके बिना यह दुष्कर कर्म कौन करे ?)

(ख) प्राणेभ्योऽपि प्रियः सुहृत्।
(प्राणों से भी प्यारा मित्र (होता है)।)
उत्तरम् :
प्राणेभ्योऽपि प्रियः कः ?
(प्राणों से भी प्यारा कौन है?)

(ग) आर्यस्य प्रसादेनं मे वणिज्या अखण्डिता।
(आर्य की कृपा से मेरा व्यापार निर्बाध है।)
उत्तरम् :
कस्य प्रसादेन मे वणिज्या अखण्डिता।
(किसकी कृपा से मेरा व्यापार निर्बाध है ?)

(घ) प्रीताभ्यः प्रकृतिभ्यः राजानः प्रतिप्रियमिच्छन्ति।
(प्रसन्नस्वभाव वालों से राजा लोग प्रत्युपकार का बदला चाहते
उत्तरम् :
प्रीताभ्यः प्रकृतिभ्यः के प्रतिप्रियमिच्छन्ति ?
(प्रसन्न स्वभाव वालों से कौन प्रत्युपकार का बदला चाहते हैं ?)

(ङ) तणानाम् अग्निना सह विरोधो भवति।
(तिनकों का आग के साथ विरोध होता है।)
उत्तरम् :
केषाम् अग्निना सह विरोधो भवति ?
(किनका अग्नि के साथ विरोध होता है ?)

प्रश्न 4.
यथानिर्देशमुत्तरत् –
(क) ‘अखण्डिता मे वणिज्या’- अस्मिन् वाक्ये क्रियापदं किम्?
(ख) पूर्वम् ‘अनृतम्’ इदानीम् आसीत् इति परस्परविरुद्ध वचने – अस्मात् वाक्यात् ‘अधुना’ इति पदस्य समानार्थकपदं चित्वा लिखत।
(ग) ‘आर्य! किं मे भयं दर्शयसि’ अत्र ‘आर्य’ इति सम्बोधनपदं कस्मै प्रयुक्तम्?
(घ) ‘प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः’ अस्मिन् वाक्ये कर्तृपदं किम्?
(ङ). तस्मिन् समये आसीदस्मद्गृहे’ अस्मिन् वाक्ये विशेष्यपदं किम्?
उत्तरम् :
(क) अखण्डिता
(ख) इदानीम्
(ग) चाणक्याय
(घ) राजानः
(ङ) गृहे।

प्रश्न 5. निर्देशानुसारम् सन्धि/सन्धिविच्छेदं कुरुत –
(निर्देश के अनुसार सन्धि/सन्धि-विच्छेद कीजिए)
(क) यथा – कः + अपि = कोऽपि
प्राणेभ्यः + अपि = …………
………. + अस्मि = सज्जोऽस्मि
आत्मनः + ………. = आत्मनोऽधिकारसदृशम्।
उत्तरम् :
प्राणेभ्यः + अपि = प्राणेभ्योऽपि
सज्जः + अस्मि = सज्जोऽस्मि
आत्मनः + अधिकारसदृशम् = आत्मनोऽधिकारसदृशम्।

(ख) यथा – सत् + चित् = सच्चित्।
शरत् + चन्द्रः = ……………..।
कदाचित् + च = ……………..।
उत्तरम् :
शरत् + चन्द्रः = शरच्चन्द्रः।
कदाचित् + च = कदाचिच्च।

प्रश्न 6.
कोष्ठकेषु दत्तयोः पदयोः शुद्धं विकल्पं विचित्य रिक्तस्थानानि पूरयत –
(कोष्ठकों में दिए हुए दो पदों में से शुद्ध विकल्प चुनकर रिक्तस्थानों की पूर्ति कीजिए)
(क) …………… विना इदं दुष्करं कः कुर्यात् ? (चन्दनदासस्य/चन्दनदासेन)
उत्तरम् :
चन्दनदासेन

(ख) …………… इदं वृत्तान्तं निवेदयामि। (गुरवे/गुरोः)
उत्तरम् :
गुरवे

(ग) आर्यस्य ……….. अखण्डिता मे वणिज्या। (प्रसादात्/प्रसादेन)
उत्तरम् :
प्रसादेन

(घ) अलम् ……………। (कलहेन/कलहात्)
उत्तरम् :
कलहेन।

(ङ) वीरः …………… बालं रक्षति। (सिंहेन/सिंहात्)
उत्तरम् :
सिंहात्।

(च) ………. भीतः मम भ्राता सोपानात् अपतत्।। (कुक्कुरेण/कुक्कुरात्)
उत्तरम् :
कुक्कुरात्।

(छ) छात्रः …………… प्रश्नं पृच्छति। (आचार्यम्/आचार्येण)
उत्तरम् :
आचार्यम्।

प्रश्न 7.
अधोदत्तमञ्जूषातः समुचितपदानि गृहीत्वा विलोमपदानि लिखत –
(नीचे दिए गए मञ्जूषा (बॉक्स) से उचित पद लेकर विलोम पद लिखिए)
[असत्यम्, पश्चात्, गुणः, आदरः, तदानीम्, तत्र पदानि]
(क) अनादरः ………..
(ख) गुणः ………..
(ग) पश्चात् ………..
(घ) असत्यम् ………..
(ङ) तदानीम् ………..
(च) तत्र ………..
उत्तराणि :
(क) आदरः
(ख) दोषः
(ग) पूर्वम्
(घ) सत्यम्
(ङ) इदानीम्
(च) अत्र

प्रश्न 8.
उदाहरणमनुसृत्य अधोलिखितानि पदानि प्रयुज्य पञ्चवाक्यानि रचयत –
(उदाहरण के अनुसार निम्न पदों का प्रयोग करके पाँच वाक्य बनाइए-)
यथा – निष्क्रम्य – शिक्षिका पुस्तकालयात् निष्क्रम्य कक्षां प्रविशति।
पदानि –
(क) उपसृत्य ……………….
(ख) प्रविश्य ………………
(ग) द्रष्टुम् …………………
(घ) इदानीम् ……………..
(ङ) अत्र ………………
उत्तराणि :
(क) उपसत्य स आह, एषः श्रेष्ठी चन्दनदासः।
(ख) वने प्रविश्य रामः पर्णकुटीम् अरचयत्।
(ग) अहं त्वां द्रष्टुम् इच्छामि।
(घ) इदानीं भवान् कुत्र गच्छति ?
(ङ) अत्र मम विद्यालयः स्थितः।

JAC Class 10th Sanskrit प्राणेभ्योऽपि प्रियः सुहृद् Important Questions and Answers

शब्दार्थ चयनम् –

अधोलिखित वाक्येषु रेखांकित पदानां प्रसङ्गानुकूलम् उचितार्थ चित्वा लिखत –

प्रश्न 1.
वत्स ! मणिकारश्रेष्ठिनं चन्दनदासमिदानीं द्रष्टुमिच्छामि।
(अ) रत्नकार
(ब) तथेति
(स) श्रेष्ठिन्
(द) परिक्रामतः
उत्तरम् :
(अ) रत्नकार

प्रश्न 2.
उपाध्याय ! अयं श्रेष्ठी चन्दनदासः।
(अ) स्वागतं ते
(ब) गुरुदेव
(स) आत्मगतम्
(द) वणिज्या
उत्तरम् :
(ब) गुरुदेव

प्रश्न 3.
नन्दस्यैव अर्थसम्बन्धः प्रीतिमुत्पादयति।
(अ) नन्दराज्यम्
(ब) नन्दस्यैव
(स) धनस्य सम्बधः
(द) उत्पादयति
उत्तरम् :
(स) धनस्य सम्बधः

प्रश्न 4.
पुनरधन्यो राज्ञो विरुद्ध इति आर्येणावगम्यते ?
(अ) श्रेष्ठिन्!
(ब) आज्ञापयतु
(स) प्रथमम्
(द) नृपस्य
उत्तरम् :
(द) नृपस्य

प्रश्न 5.
अयमीदृशो विरोधः यत् त्वमद्यापि-
(अ) मतभेदः
(ब) राजापथ्यकारिणः
(स) स्वगृहे
(द) निवेदितम्
उत्तरम् :
(अ) मतभेदः

प्रश्न 6.
गृहेषु गृहजनं निक्षिप्य देशान्तरं व्रजन्ति।
(अ) इच्छतामपि
(ब) स्थापयित्वा
(स) दोषमुत्पादयति।
(द) परस्परं
उत्तरम् :
(ब) स्थापयित्वा

प्रश्न 7.
भो श्रेष्ठिन् ! शिरसि भयम्, अतिदूरं तत्प्रतिकारः।
(अ) इदानीम्
(ब) कथम् न
(स) मस्तके
(द) तंदुलः
उत्तरम् :
(स) मस्तके

प्रश्न 8.
चन्दनदास ! एष एव ते निश्चयः ?
(अ),समर्पयामि
(ब) अयम्
(स) त्वम्
(द) तव
उत्तरम् :
(द) तव

प्रश्न 9.
क इदं दुष्करं कुर्यादिदानीं शिविना विना –
(अ) कठिन।
(ब) स्वगतम्
(स) साधुः
(द) अतिदूरम्
उत्तरम् :
(अ) कठिन।

प्रश्न 10.
ननु भवता प्रष्टव्याः स्मः –
(अ) निश्चितमेव
(ब) राज्ञो विरुद्धः
(स) प्रथमम्
(घ) पिधाय
उत्तरम् :
(अ) निश्चितमेव

संस्कृतमाध्यमेन प्रश्नोत्तराणि –

एकपदेन उत्तरत (एक शब्द में उत्तर दीजिए)

प्रश्न 1.
चाणकस्य कृपया कस्य वणिज्या अखण्डिता ?
(चाणक्य की कृपा से किसका व्यापार बाधारहित था ?)
उत्तरम् :
चन्दनदासस्य (चन्दनदास का)।

प्रश्न 2.
कः सम्बन्धः प्रीतिमुत्पादयति ?
(कौनसा सम्बन्ध प्रेम पैदा करता है ?)
उत्तरम् :
अर्थसम्बन्धः (धन का संबंध)।

प्रश्न 3.
कुत्र अविरुद्धवृत्तिः ?
(कहाँ विरोध रहित स्वभाव वाले बनो ?)
उत्तरम् :
राजनि (राजा के प्रति)।

प्रश्न 4.
केन चन्दनदासो राज्ञो विरुद्ध इति अवगम्यते ?
(कौन ‘चन्दनदास राजा के विरुद्ध है’ यह जानता है? )
उत्तरम् :
चाणक्यः (चाणक्य)।

प्रश्न 5.
अमात्यराक्षसस्य गृहजनः का क्या गृहे असीत ?
(अमात्य राक्षस के घरवाले किसके घर में थे ?)
उत्तरम् :
चन्दनदासस्य (चन्दनदास के)।

प्रश्न 6.
चन्दनदासानुसारम् अलीकम चायनसाय क्रेन निवेदितम् ?
(चन्दनदास के अनुसार चाणवले मिथ्या किसने कहा ?)
उत्तरम् :
केनाप्यनार्येण (किलो दुष्ट थे)।

प्रश्न 7.
चन्दनदासस्य दुष्कर कार्य किमामील ?
(चन्दनदास का दुष्कर कार्य क्या था ?)
उत्तरम् :
निश्चयः (निश्चय)।

प्रश्न 8.
‘क इदं दुष्करं कुर्यादिदानीं शिविना विना’ अत्र किं क्रियापदम् ?
(‘क इदं दुष्करं कुर्यादिदानी शिविना विना’ यहाँ क्रियापद क्या है ?)
उत्तरम् :
कुर्यात् (करे)।

प्रश्न 9.
मणिकारश्रेष्ठिनं कः द्रष्टुम् इच्छति ?
(जौहरी सेठ से कौन मिलना चाहता है ?)
उत्तरम् :
चाणक्यः (चाणक्य)।

प्रश्न 10.
चाणक्यः कं द्रष्टुम् इच्छति ?
(चाणक्य किससे मिलना चाहता है ?)
उत्तरम् :
चन्दनदासम् (चन्दनदास से)।

प्रश्न 11.
चाणक्यानुसारं चन्दनदासः राजानं प्रति कीदृशः भवितव्य ?
(चाणक्य के अनुसार चन्दनदास राजा के प्रति कैसा हो?)
उत्तरम् :
अविरुद्धवृत्तिर्भव (विरोध रहित स्वभाव वाले।)

प्रश्न 12.
कस्तावत् प्रथमम् ? (कौन प्रमुख है?)
उत्तरम् :
भवान् (आप, चन्दनदास)।

प्रश्न 13.
के भीताः देशान्तरं व्रजन्ति ?
(डरे हुए कौन परदेश जाते हैं ?)
उत्तरम् :
राजपुरुषाः (राजपुरुष)।

प्रश्न 14.
चाणक्यानुसारं चन्दनदासस्य वचने कीदृशे आस्ताम् ?
(चाणक्य के अनुसार चन्दनदास के दोनों वचन कैसे थे ?)
उत्तरम् :
परस्परविरुद्धे (दोनों परस्पर विरुद्ध)।

प्रश्न 15.
चन्दनदासः कस्य गृहजनं न समर्पयति ?
(चन्दनदास किसके परिवारीजनों को नहीं सौंपता है?)
उत्तरम् :
राक्षसस्य (राक्षस के)।

प्रश्न 16.
अस्मिन् नाट्यांशे चन्दनदासस्य तुलना केन सह कृता ?
(इस नाट्यांश में चन्दनदास कीतुलना किसके साथ की गई है ?)
उत्तरम् :
शिविना (शिवि से)।

पूर्णवाक्येन उत्तरत (पूरे वाक्य में उत्तर दीजिए)

प्रश्न 17.
चन्दनदासः काम् आज्ञाम् इच्छति ?
(चन्दनदास क्या आज्ञा चाहता है ?)
उत्तरम् :
चन्दनदास: ‘किं कियत् च अस्मज्जनादिश्यते’ इति आज्ञाम् इच्छति।
(चन्दनदास ने ‘क्या और कितना हम लोगों को आदेश दिया जाता है’ ऐसी आज्ञा चाहता है।)

प्रश्न 18.
चन्दनदासेन चाणक्यः किं प्रष्टव्यः ?
(चन्दनदास से चाणक्य क्या पूछता है?)
उत्तरम् :
यो श्रेष्ठिन ! स चापरिक्लेशः कथमाविर्भवति ?
(सेठजी, वह सुख किस प्रकार प्राप्त होता है ?)

प्रश्न 19.
चन्दनदासः कर्णौ पिधाय किम् अवदत्?
(चन्दनदास कानों को ढंककर क्या बोला ?)
उत्तरम् :
चन्दनदासः कर्णौ पिधाय अवदत्-शान्तं पापम्, शान्तं पापम्। कीदृशस्तृणानामाग्निना सह विरोधः?
(कानों पर हाथ रखकर चन्दनदास ने कहा- पाप शान्त हो, पाप शांत हो तिनकों के साथ आग का कैसा विरोध ?)

प्रश्न 20.
अमात्यराक्षसस्य गृहजनविषये चन्दनदासः कथं स्वीकरोति ?
(अमात्य राक्षस के घरवालों के विषय में चन्दनदास कैसे स्वीकार करता है ?)
उत्तरम् :
‘तस्मिन् समये तु अमात्यराक्षसस्य गृहजनः मम गृहे आसीत्’ इदानीं क्व गतः, न जानामि।
(उस समय तो अमात्य राक्षस के घरवाले मेरे घर में थे, अब कहाँ गये, नहीं जानता हूँ।)

प्रश्न 21.
चन्दनदासः कोऽस्ति ?
(चन्दनदास कौन है ?)
उत्तरम् :
चन्दनदासः मणिकारः श्रेष्ठी अस्ति।
(चन्दनदास जौहरी सेठ है।)

प्रश्न 22.
अविरुद्धवत्तिः कस्मिन भवेत ?
(किसके प्रति अनकल व्यवहार करने वाला होना चाहिए ?)
उत्तरम् :
राजनि अविरुद्धवृत्तिर्भवेत्।
(राजा के प्रति अनुकूल व्यवहार करने वाला होना चाहिए।)

प्रश्न 23.
भीताः पूर्वराजपुरुषाः किं कुर्वन्ति ?
(डरे हुए पूर्व राजपुरुष क्या करते हैं?)
उत्तरम् :
भीताः पूर्वराजपुरुषाः पौराणामिच्छतामपि गृहेषु गृहजनं निक्षिप्य देशान्तरं व्रजन्ति।
(डरे हुए पूर्व राजपुरुष नगरवासियों के चाहने पर भी उनके घरों पर स्वजनों को रखकर परदेश चले जाते हैं।)

प्रश्न 24.
“किं मे भयं दर्शयसि” इति कः कं प्रति कथयति?
(…. कौन किसके प्रति कहता है ?)
उत्तरम् :
चन्दनदासः चाणक्यं प्रति कथयति।
(चन्दनदास चाणक्य के प्रति कहता है।)

अन्वय-लेखनम् –

अधोलिखितश्लोकस्यान्वयमाश्रित्य रिक्तस्थानानि मञ्जूषातः समुचितपदानि चित्वा पूरयत।
(नीचे लिखे श्लोक के अन्वय के आधार पर रिक्तस्थानों की पूर्ति मंजूषा से उचित पद चुनकर कीजिए।)
सुलभेष्वर्थलाभेषु ……………. …………………. शिविना विना।।

मञ्जूषा – सुलभेषु, संवेदने, शिविना, कः।

परस्य (i)……… अर्थलाभेषु (ii)……… इदं दुष्करं कर्म जने (लोके) (iii)……… विना (iv)……… कुर्यात्।
उत्तरम् :
(i) संवेदने (ii) सुलभेषु (iii) शिविनाः (iv) कः।

प्रश्ननिर्माणम् –

अधोलिखित वाक्येषु स्थूलपदमाधृत्य प्रश्ननिर्माणं कुरुत –

1. चाणक्यः मणिकारश्रेष्ठिनं चन्दनदासं द्रष्टुमिच्छति।
(चाणक्य रत्नकार चन्दनदास को देखना चाहता है।)
2. शिष्यः चन्दनदासेन सह प्रविशति।
(शिष्य चन्दनदास के साथ प्रवेश करता है।)
3. आर्यस्य प्रसादेन अखण्डिता मे वणिज्या।
(आर्य की कृपा से मेरा व्यापार निर्विघ्न है।)
4. राजानः प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति।
(राजा लोग प्रसन्न प्रकृति वाले का प्रत्युपकार करते हैं।)
5. नन्दस्य अर्थसम्बन्धः प्रीतिमुत्पादयति।
(नन्द का अर्थ सम्बन्ध प्रीति पैदा करता है।)
6. राजनि अविरुद्धवृत्तिर्भवेत्।
(राजा में विरोधी प्रवृत्ति वाला नहीं होना चाहिए।)
7. भीताः पूर्वराजपुरुषाः गृहजनं निक्षिप्य देशान्तरं व्रजन्ति।
(डरे हुए पूर्व राजपुरुष घरवालों (स्वजनों) को रखकर परदेश चले जाते हैं।)
8. अग्निना सह तृणानां विरोधः।
(अग्नि के साथ तिनकों (घास) का विरोध है।)
9. प्राणेभ्योऽपि प्रियः सुहत्।
(प्राणों से भी प्रिय स्वजन होता है।)
(माध्यमिक परीक्षा, 2013)
10. अत्यादरः शङ्कनीयः।
(अधिक आदर शंका करने योग्य होता है।)
उत्तराणि :
1. चाणक्यः कं द्रष्टुम् इच्छति ?
2. शिष्यः केन सह प्रविशति ?
3. कस्य प्रसादेन अखण्डिता मे वणिज्या ?
4. राजानः काभ्यः प्रतिप्रियमिच्छन्ति ?
5. कस्य अर्थसम्बन्धः प्रीतिम् उत्पादयति ?
6. कस्मिन् अविरुद्धवृत्तिर्भवेत् ?
7. के गृहजनं निक्षिप्य देशान्तरं व्रजन्ति ?
8. केन सह तृणानां विरोधः ?
9. कः प्राणेभ्योऽपि प्रियः ?
10. कः शङ्कनीयः ?

भावार्थ-लेखनम् –

अधोलिखित पद्यांश संस्कृते भावार्थं लिखत सुलभेष्वर्थलाभेषु ……………………………कुर्यादिदानीं शिविना विना।।

भावार्थ – अन्यस्य वस्तु समर्पिते कृते, धन प्राप्तेषु, सहजेषु सत्सु एतत् स्वार्थं त्यक्त्वा परस्य वस्तु रक्षणं-कर्त्तव्यम् लोके कठिनम्, शिविमन्तरेण कः सम्पादयेत्।।

अधोलिखितानां सूक्तीनां भावबोधनं सरलसंस्कृतभाषया लिखत –
(निम्नलिखित सूक्तियों का भावबोध सरल संस्कृत भाषा में लिखिए-)

(i) अत्यादरः शङ्कनीयः।

भावार्थः – यः मनुष्यः अत्यधिकम् आदरं करोति, सः वञ्चनप्रयोजनेन करोति अतः अत्यधिक: आदरः शङ्कां जनयति। (जो मनुष्य अत्यधिक आदर करता है, वह छलने के प्रयोजन से करता है। अत: अधिक आदर शंका को पैदा करता है।)

(ii) प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः।

भावार्थ: – प्रसन्नेभ्यः प्रजाजनेभ्यः नृपाः प्रतिकाररूपेण आत्मानं प्रति अपि प्रियम् एव इच्छन्ति।
(प्रसन्न प्रजाजनों से राजा लोग बदले में अपने लिए भी प्रिय ही चाहते हैं।)

(iii) राजनि अविरुद्धवृत्तिर्भव।

भावार्थ: – प्रजाजनैः सदैव राजानं प्रति अनुकूलवृत्तिः एव भवेत्।
(प्रजाजनों को सदैव राजा के प्रति अनुकूल व्यवहार वाला ही होना चाहिए।)

(iv) कः पुनरधन्यो राज्ञो विरुद्धः।

भावार्थ: – कोऽपि मनुष्यः नृपस्य प्रतिकूलं कार्यं न कुर्यात्। यः नृपस्य विरुद्धः भवति सः धन्यः न भवति। (किसी भी मनुष्य को राजा के प्रतिकूल कार्य नहीं करना चाहिए। जो राजा के विरुद्ध होता है वह धन्य नहीं होता।)

(v) कीदृशस्तृणानाम् अग्निना सह विरोधः।

भावार्थ: – अग्निः तु तृणान् ज्वालयति, यतः असौ सामर्थ्यवान् भवति अत: अग्निना सह तृणानां विरोधः कथं सम्भवति तथैव नृपैः सह अपि प्रजाजनानां वैरम् अपि असम्भवः। (आग तो घास को जलाती है। क्योंकि वह सामर्थ्यवान् होती है अतः आग के साथ तिनकों का विरोध कैसे सम्भव हो सकता है। उसी प्रकार राजाओं के साथ प्रजाजनों का वैर भी असम्भव है।)

प्राणेभ्योऽपि प्रियः सुहृद् Summary and Translation in Hindi

पाठ-परिचय – ‘काव्येषु नाटकं रम्यम्’ ऐसी उक्ति प्रसिद्ध है। संस्कृत साहित्य में नाटकों की एक लम्बी श्रृंखला है जिसमें विविध नाटकों की कड़ियाँ जुड़ी हुई हैं। इन्हीं नाटकों में कूटनीति एवं राजनीति से भरपूर एक प्रसिद्ध नाटक है ‘मुद्राराक्षसम्’। प्रस्तुत पाठ ‘प्राणेभ्योऽपि प्रियः सुहृद्’ महाकवि विशाखदत्त रचित ‘मुद्राराक्षसम्’ के प्रथम अंक से सङ्कलित है। नन्दवंश का विनाश करने के बाद उसके हितैषियों को खोज-खोजकर पकड़वाने के क्रम में चाणक्य, अमात्य राक्षस एवं उसके परिजनों की जानकारी प्राप्त करने के लिए चन्दनदास से वार्तालाप करते हैं किन्तु चाणक्य को अमात्य राक्षस के विषय में कोई सुराग न देता हुआ चन्दनदास अपनी मित्रता पर दृढ़ रहता है।

उसके मैत्री भाव से प्रसन्न होते हुए भी चाणक्य जब उसे राजदण्ड का भय दिखाता है तब चन्दनदास राजदण्ड भोगने के लिए सहर्ष प्रस्तुत हो जाता है। इस प्रकार अपने मित्र के लिए प्राणों का भी उत्सर्ग करने के लिए तत्पर चन्दनदास अपनी सुहृद्-निष्ठा का एक ज्वलंत उदाहरण प्रस्तुत करता है।

मूलपाठः,शब्दार्थाः, सप्रसंग हिन्दी-अनुवादः

1.

• चाणक्यः – वत्स ! मणिकारश्रेष्ठिनं चन्दनदासमिदानीं द्रष्टुमिच्छामि।
• शिष्यः – तथेति (निष्क्रम्य चन्दनदासेन सह प्रविश्य) इतः इतः श्रेष्ठिन् (उभौ परिक्रामतः)
• शिष्यः – (उपसृत्य) उपाध्याय ! अयं श्रेष्ठी चन्दनदासः।
• चन्दनदासः – जयत्वार्यः
• चाणक्यः – श्रेष्ठिन् ! स्वागतं ते। अपि प्रचीयन्ते संव्यवहाराणां वृद्धिलाभाः ?
• चन्दनदासः – (आत्मगतम्) अत्यादरः शङ्कनीयः। (प्रकाशम्) अथ किम्। आर्यस्य प्रसादेन अखण्डिता मे वणिज्या।
• चाणक्यः – भो श्रेष्ठिन् ! प्रीताभ्यः प्रकृतिभ्यः प्रतिप्रियमिच्छन्ति राजानः।
• चन्दनदासः – आज्ञापयतु आर्यः, किं कियत् च अस्मज्जनादिष्यते इति।

शब्दार्थाः = वत्स ! = पुत्र ! (बेटा)। मणिकारश्रेष्ठिनम् = रत्नकारं वणिजम्, रत्नानां व्यवसायिनम् (रत्नों के व्यापारी)। चन्दनदासमिदानीम् = चन्दनदास इत्याख्यम् अधुना (चन्दनदास नामक को अब)। द्रष्टुमिच्छामि = परामृष्टुं वाञ्छामि (मिलना चाहता हूँ )। तथेति = तथैव भवतु (वैसा ही हो)। निष्क्रम्य = बहिर्गत्वा (बाहर निकलकर)। चन्दनदासेन सह प्रविष्य = चन्दनदासेन श्रेष्ठिना सार्धं प्रवेशं कृत्वा (चन्दनदास के साथ प्रवेश करके)। इतः इतः = अत्र एहि (इधर-इधर आएँ)।

श्रेष्ठिन् = हे धनिक ! (हे सेठ जी !)। उभौ = द्वावेव (दोनों)। परिक्रामतः = घूमते हैं। उपसृत्य = समीपं गत्वा (पास जाकर)। उपाध्याय ! = हे गुरुदेव ! (हे गुरु जी !)। अयम् = एषः (यह)। श्रेष्ठी = धनिकः (सेठ)। जयत्वार्यः = विजयतामार्यः (आर्य की जय हो)। स्वागतं ते = अभिनन्दन भवतः (आपका स्वागत है)। अपि = किम् (क्या)। प्रचीयन्ते = वृद्धिं प्राप्नुवन्ति (बढ़ रहे हैं)। संव्यवहाराणां = व्यापाराणाम् (व्यापारों का)। वृद्धिलाभाः = लाभ वृद्धयः (लाभांशों की वृद्धि)। आत्मगतम् = मनसि एव (मन ही मन)। अत्यादरः = अत्यधिक: सम्मानः (अत्यधिक आदर)।

शङ्कनीयः = सन्देहास्पदम् (शंका करने योग्य है)। प्रकाशम् = प्रकटम् (सबके समक्ष)। अथ किम् = आम् कथन्न (जी हाँ, क्यों नहीं)। आर्यस्य = श्रीमतः (आर्य की)। प्रसादेन = कृपया (कृपा से)। अखण्डिताः = निर्बाधः (बाधा रहित हैं)। मे = मम (मेरे)। वणिज्या = व्यवसायाः वाणिज्यम् (व्यापार)। भो श्रेष्ठिन्! = रे धनिक ! (अरे सेठ जी !)। प्रीताभ्यः = प्रसन्नाभ्यः (प्रसन्नजनों के प्रति)। प्रकृतिभ्यः = प्रजायैः (प्रजा के लिये)। प्रतिप्रियमिच्छन्ति = प्रत्युपकारम् वाञ्छन्ति (उपकार के बदले उपकार करना चाहते हैं)। राजानः = नृपाः (राजा लोग)। आज्ञापयतु आर्यः = श्रेष्ठजनः आज्ञां देहि, आदिशतु (आर्य आज्ञा दें, आदेश दें)। किं कियत् च = किं कियन्मानञ्च (क्या और कितना)। अस्मज्जनादिष्यते = अस्मभ्यम् आज्ञां दीयते (हमें आज्ञा दी जाती है)।

सन्दर्भ-प्रसङ्गश्च – यह नाट्यांश हमारी शेमुषी पाठ्य-पुस्तक के ‘प्राणेभ्योऽपि प्रियः सहृद’ पाठ से लिया गया है। मूलतः यह पाठ महाकवि विशाखदत्त रचित ‘मुद्राराक्षसम्’ नाटक के पहले अंक से सङ्कलित है। इस नाट्यांश में चाणक्य मणिकार चन्दनदास से मिलना चाहता है परन्तु चन्दनदास इस अत्यादर में शङ्का करता है।

हिन्दी-अनुवादः :

• चाणक्य – बेटा (वत्स) ! अब मैं रत्नों के व्यापारी चन्दनदास से मिलना चाहता हूँ।
• शिष्य – वैसा ही हो। (बाहर निकलकर और चन्दनदास के साथ प्रवेश करके) इधर, इधर (आइए) सेठ जी ! (दोनों घूमते हैं)।
• शिष्य – (पास जाकर) गुरुदेव ! यह सेठ चन्दनदास है।
• चन्दनदास – आर्य की जय हो।
• चाणक्य – सेठ जी ! आपका स्वागत है। क्या व्यापार में आपकी लाभवृद्धियाँ बढ़ रही हैं ?
• चन्दनदास – (मन ही मन) अत्यधिक आदर शंका करने योग्य होता है। (प्रकट में) जी हाँ, आर्य की कृपा से मेरे व्यापार बाधारहित हैं।
• चाणक्य – अरे सेठ जी ! प्रसन्न स्वभाव से लोगों के लिए राजा प्रत्युपकार चाहते हैं।
• चन्दनदास – आर्य आज्ञा दें, क्या और कितना हमारे लिए आदेश दिया जाता है।

2 चाणक्यः – भो श्रेष्ठिन् ! चन्द्रगुप्तराज्यमिदं न नन्दराज्यम्। नन्दस्यैव अर्थसम्बन्धः प्रीतिमुत्पादयति।
चन्द्रगुप्तस्य तु भवतामपरिक्लेश एव।
चन्दनदासः – (सहर्षम्) आर्य ! अनुगृहीतोऽस्मि।
चाणक्यः – भो श्रेष्ठिन् ! स चापरिक्लेशः कथमाविर्भवति इति ननु भवता प्रष्टव्याः स्मः।
चन्दनदासः – आज्ञापयतु आयः।।
चाणक्यः – राजनि अविरुद्धवृत्तिर्भव।
चन्दनदासः – आर्य ! कः पुनरधन्यो राज्ञो विरुद्ध इति आर्येणावगम्यते ?
चाणक्यः – भवानेव तावत् प्रथमम्।
चन्दनदासः – (कर्णी पिधाय) शान्तं पापम्, शान्तं पापम्। कीदृशस्तृणानामग्निना सह विरोध: ?

शब्दार्थाः – भो श्रेष्ठिन् = हे धनिक ! (अरे सेठ जी)। चन्द्रगुप्तराज्यमिदम् = चन्द्रगुप्तस्य एतद् शासनम् (यह चन्द्रगुप्त का राज्य है)। न नन्दराज्यम् = न तु नंदस्य शासनम् (न कि नन्द का राज्य)। नन्दस्यैव = नन्दस्य राज्यम् एव (नंद के राज्य में ही)। अर्थसम्बन्धः = धनस्य सम्बन्धः (धन के प्रति लगाव)। प्रीतिमुत्पादयति = स्नेहं जनयति (स्नेह पैदा करता है)। चन्द्रगुप्तस्य तु = चन्द्रगुप्तमौर्यस्य तु (चन्द्रगुप्त मौर्य का तो)। भवताम् = युष्माकम् (आपका)। अपरिक्लेश एव = दुःखाभावः एव (दुःख का अभाव ही है)। सहर्षम् = प्रसन्नतासहितम् (प्रसन्नता के साथ)। अ = श्रीमन् ! (हे श्रीमान् जी!)।

अनगृहीतोऽस्मि = सानुकम्पोऽस्मि (अनुगृहीत हुआ हूँ )। भो श्रेष्ठिन! = हे वणिक ! (अरे सेठ जी!)। स चापरिक्लेशः = असौ च दुःखाभावः (और वह दुःख का अभाव)। कथमाविर्भवति = कथम् अवतरितः (कैसे अवतरित होता है)। इति ननु भवता = एवं निश्चितमेव त्वया (इस प्रकार निश्चय ही आपके द्वारा)। प्रष्टव्याः स्मः = प्रष्टुं योग्याः स्मः (पूछने योग्य हैं)। आज्ञापयतु आर्यः = आर्यः आदिशतु (आर्य आदेश दें)। राजनि = नृपे (राजा में, राजा के प्रति)। अविरुद्धवत्तिर्भव = अविरुद्धस्वभावः भव (विरोध-रहित स्वभाव वाले बनो)।

आर्य ! = हे श्रीमन् !(हे श्रीमान् जी!)। कः पुनरधन्यो = पुनः कः हतभाग्यः (फिर कौन अभागा)। राज्ञो विरुद्धः = नृपस्य विरोधे (राजा के विरोध में)। अस्ति = है। इति आर्येणावगम्यते – इति देवेन ज्ञायते (इसे श्रीमान् द्वारा जाना जाता है, अर्थात् आप इसे जानते हैं)। भवान् एव = त्वम् एव, श्रीमान् एव (आप ही)। तावत् = तर्हि (तो)। प्रथमम् = प्रमुखः (प्रमुख हैं)। कर्णी = श्रवणौ (कानों को)। पिधाय = आच्छाद्य (बन्द करके)। शान्तं पापम् = अघः नश्यतु (पाप शान्त हो)। कीदृशस्तृणानामग्निना सह विरोधः = अनलेन सह घासस्य/तृणस्य कीदृशः मतभेदः (अग्नि के साथ तिनके का क्या विरोध)।

सन्दर्भ-प्रसङ्गश्च – यह नाट्यांश हमारी शेमुषी पाठ्य-पुस्तक के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से लिया गया है। मूलत: यह पाठ महाकवि विशाखदत्त रचित ‘मुद्राराक्षसम्’ नाटक के प्रथम अंक से सङ्कलित है। इस नाट्यांश में चाणक्य और चन्दनदास के संवाद के बहाने प्रसंग आरंभ किया जाता है।

हिन्दी-अनुवादः –

• चाणक्य – अरे सेठ जी ! यह चन्द्रगुप्त मौर्य का राज्य है न कि नन्द का राज्य। नन्द के राज्य में ही धन के प्रति लगाव स्नेह पैदा करता है। चन्द्रगुप्त मौर्य के (राज्य में) तो आपको दुःख का अभाव ही है।
• चन्दनदास – (प्रसन्नता के साथ) आर्य ! मैं अनुगृहीत हुआ।
• चाणक्य – अरे सेठ जी ! और वह दुःख का अभाव अति सुख कैसे उत्पन्न होता है, यह आपको निश्चित ही हमसे पूछना चाहिए।
• चन्दनदास – आर्य ! आदेश दें।
• चाणक्य – राजा के प्रति अविरोधी (विरोधहीन अर्थात् अनुकूल) व्यवहार वाले बनो।
• चन्दनदास – आर्य ! फिर ऐसा कौन अभागा है जो राजा का विरोधी हो। ऐसा श्रीमान् जानते ही हैं आप ही बताएँ।
• चाणक्य – प्रथम (प्रमुख) तो आप ही हैं।
• चन्दनदास – (कानों को बन्द करके अर्थात् कानों पर हाथ रखकर) पाप शान्त हो, पाप शान्त हो (अरे राम, राम) तिनकों के साथ आग का कैसा विरोध ?

3 चाणक्यः – अयमीदृशो विरोधः यत् त्वमद्यापि राजापथ्यकारिणोऽमात्यराक्षसस्य गृहजनं स्वगृहे रक्षसि।
चन्दनदासः – आर्य ! अलीकमेतत्। केनाप्यनार्येण आर्याय निवेदितम्।।
चाणक्यः – भो श्रेष्ठिन् ! अलमाशङ्कया। भीताः पूर्वराजपुरुषाः पौराणामिच्छतामपि गृहेषु गृहजनं निक्षिप्य देशान्तरं व्रजन्ति। ततस्तत्तच्छादनं दोषमुत्पादयति।
चन्दनदासः – एवं नु इदम्। तस्मिन् समये आसीदस्मद्गृहे अमात्यराक्षसस्य गृहजन इति।
चाणक्यः – पूर्वम् ‘अनृतम्’, इदानीम् ‘आसीत्’ इति परस्परविरुद्ध वचने।
चन्दनदासः – आर्य ! तस्मिन् समये आसीदस्मद्गृहे अमात्यराक्षस्य गृहजन इति।

शब्दार्थाः – अयम् = एषः (यह)। ईदृशो = अस्य प्रकारस्य, एतद्विधः (ऐसा, इस प्रकार का)। विरोधः = मतभेदः (विरोध)। यत् त्वमद्यापि = यद् भवान् अधुनापि (कि आप अब, आज भी)। राजापथ्यकारिणः = नृपस्य अपकारिणः (राजा का अहित करने वाले)। अमात्यराक्षसस्य = मन्त्रिणः राक्षसस्य (मन्त्री राक्षस के)। गृहजनम् = परिवारिजनम् (परिवार वालों की)। स्वगृहे = आत्मनः भवने (अपने घर में)। रक्षसि = रक्षां करोति (रक्षा करते हो)। आर्य ! = (हे महोदय!)। अलीकमेतत् = असत्यम् इदम्, अनृतमिदम् (यह झूठ है)। केनाप्यनार्येण = कोऽपि दुष्टः (किसी दुष्ट ने)।

आर्याय = महोदयाय (आर्य से)। निवेदितम् = निवेदितवान् (निवेदन किया है; कहा है)। भो श्रेष्ठिन् = रे धनिक ! (अरे सेठजी)। अलमाशङ्कया = सन्देहस्य आवश्यकता न वर्तते, सन्देहं मा कुरु (शङ्का मत करो)। भीताः = भयाक्रान्ताः (डरे हुए)। पूर्वराजपुरुषाः = पूर्वराज्ञः सैनिकाः, पूर्वनृपस्य सेवकाः (भूतपूर्व राजा के सैनिक)। पौराणाम् = नगरवासिनाम् (नगरवासियों के)। इच्छतामपि = वाञ्छतामपि, इच्छुकानामपि (चाहने वालों के भी)। गृहेषु = भवनेषु (घरों में)। गृहजनम् = परिवारिजनान् (परिवार के लोगों को)। निक्षिप्य = स्थापयित्वा (रखकर)।

देशान्तरम् = परदेशम् (परदेश को)। व्रजन्ति = गच्छन्ति, प्रस्थानं कुर्वन्ति (चले जाते हैं)। ततः = तत्पश्चात् (उसके बाद)। तत् आच्छादनम् = तस्य गोपायनम् (उसे छिपाना, छुपाकर रखना)। दोषमुत्पादयति = अपराधं जनयति (अपराध को जन्म देता है, पैदा करता है)। एवं नु इदम् = नैवम् एत् (ऐसा नहीं है)। तस्मिन् समये = तदा (उस समय)। अस्मद् गृहे = अस्माकम् आवासे (हमारे घर पर)। अमात्यराक्षसस्य = मन्त्रिणः राक्षसस्य (अमात्य राक्षस के)। गृहजनः = परिजनः (परिवार के लोग)। आसीत् = अवर्तत (थे)। पूर्वम् = पूर्वकाले, प्रथमस्तु (पहले तो)। अनृतम् = मिथ्या, असत्यम् (झूठ)। इदानीम् = अधुना (अब)।

आसीत् = अवर्तत (था)। इति परस्परं = एवम् अन्यान्ययोः (इस प्रकार एक दूसरे .के)। विरुद्ध वचने = विपरीतकथने (विपरीत वचन होने पर)। आर्य ! = हे श्रीमन् ! (हे महोदय!)। तस्मिन् समये = तस्मिन् काले, तदा (तब, उस समय)। अस्मद्गृहे = अस्माकम् आवासे (हमारे घर में)। अमात्यराक्षसस्य = मन्त्रिणः राक्षसस्य (अमात्य राक्षस के)। गृहजनः = परिजनः (परिवार के लोग)। आसीत् = अवर्तत (था/थे)।

सन्दर्भ-प्रसङ्गश्च – यह नाट्यांश हमारी शेमुषी पाठ्य-पुस्तक के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से लिया गया है। मूलतः यह पाठ महाकवि विशाखदत्त रचित ‘मुद्राराक्षसम्’ नाटक के प्रथम अंक से सङ्कलित है। इस नाट्यांश में चाणक्य अपने कथ्य को चन्दनदास से कहता है और अन्वेषण आरम्भ कर देता है।।

हिन्दी-अनुवादः :

• चाणक्य – यह ऐसा विरोध है कि आप अब भी राजा का अहित करने वाले मन्त्री राक्षस के परिवारवालों को अपने घर में छुपाकर रक्षा करते हैं।
• चन्दनदास – आर्य ! यह (बिल्कुल) झूठ है। किसी दुष्ट ने (आपसे) ऐसा कह दिया है।
• चाणक्य – अरे सेठ जी ! शंका मत करो। भूतपूर्व राजा के डरे हुए सैनिक चाहने वाले नगरवासियों के घरों में अपने परिजनों को भी रखकर परदेश को जाते हैं। तब उस अमात्य राक्षस का छुपाना दोष या अपराध को जन्म देता है।
• चन्दनदास – ऐसा नहीं है, उस समय हमारे घर में अमात्य राक्षस के परिवार के लोग थे।
• चाणक्य – पहले ‘अनृतम्’ (झूठ) अब ‘आसीत्’ (थे) इस प्रकार आपस में (परस्पर) विरोधी वचन है।
• चन्दनदास – आर्य ! उस समय (तब) हमारे घर में अमात्य राक्षस के परिवार वाले थे (अब नहीं हैं)।

4. चाणक्यः – अथेदानी क्व गतः ?
चन्दनदासः – न जानामि।
चाणक्यः – कथं न ज्ञायते नाम ? भो श्रेष्ठिन् ! शिरसि भयम्, अतिदूरं तत्प्रतिकारः।
चन्दनदासः – आर्य! किं मे भयं दर्शयसि ? सन्तमपि गेहे अमात्यराक्षसस्य गृहजनं न समर्पयामि, किं पुनरसन्तम् ?
चाणक्यः – चन्दनदास ! एष एव ते निश्चयः ?
चन्दनदासः – बाढम्, एष एव मे निश्चयः।
चाणक्यः – (स्वगतम्) साधु ! चन्दनदास साधु।

सुलभेष्वर्थलाभेषु परसंवेदने जने।
क इदं दुष्करं कुर्यादिदानीं शिविना विना।।

शब्दार्थाः – अथ = एतत्पश्चात् (तो फिर)। इदानीम् = अधुना (अब)। क्व – कुत्र (कहाँ)। गतः = प्रस्थितः यातः (गए)। न जानामि = न मया ज्ञायते (नहीं जानता, मुझे पता नहीं)। कथम् न = कस्मात् न (क्यों नहीं)। ज्ञायते नाम = अवगम्यते (जानते हो)। भो श्रेष्ठिन् ! = रे धनिक ! (अरे सेठजी)। शिरसि = मस्तके (सिर पर)। भयम् = भीतिः (डर है)। तत्प्रतिकारं = तस्योपचारम् (उसका उपचार)। अतिदूरम् = अत्यधिकं दूरे स्थितम् (बहुत दूर पर है)। आर्य! = (हे महोदय)। किं मे भयं दर्शयति = अपि मां भयभीतं करोषि (क्या मुझे डरा रहे हो)।

सन्तमपि गेहे = गृहे विद्यमानं अपि (घर में होते हुए भी)। अमात्यराक्षसस्य = मन्त्रिणः राक्षसस्य (अमात्य राक्षस के)। गृहजनम् = परिवारस्य सदस्यान् (परिवारीजनों को)। न समर्पयामि = न प्रत्यर्पयामि (नहीं लौटाता)। किं पुनरसन्तम् = किं पुनः न निवसन्तम् (न रहने वालों का तो कहना क्या)। एष एव = अयमेव (यही)। ते = तव (तेरा)। निश्चयः = संकल्पः (निश्चय है)। बाढम् = आम् (हाँ)। एषः एव = अयमेव (यही)। मे = मम (मेरा)। निश्चयः = दृढसंकल्पः (निश्चय है)। स्वगतम् = आत्मगतम् (मन ही मन)। साधुः धन्यः = अतिसुन्दरम् (बहुत अच्छे, निश्चय ही, धन्य हो)। चन्दनदास साधु = धन्योऽसि चन्दनदास! (चन्दनदास, तुम धन्य हो)।

सुलभेष्वर्थलाभेषु …………………………. शिविना विना।।

अन्वयः – परस्य संवेदने अर्थलाभेषु सुलभेषु इदं दुष्करं कर्म जने (लोके) शिविना विना कः कुर्यात्।

शब्दार्थाः – परस्य = अन्यस्य (दूसरे की वस्तु को)। संवेदने = समर्पणे कृते सति (समर्पित करने पर)। सुलभेषु = धन प्राप्तेषु सहजेषु सत्सु (धन की प्राप्ति आसान हो जाने पर भी)। इदम् = एतद् स्वार्थं त्यक्त्वा परस्य वस्तुरक्षणम् (यह)। कर्म = कर्त्तव्यम् (कार्य)। जने = लोके (मनुष्यों में)। दुष्करम् = कठिनम् (मुश्किल है)। शिविना विना = शिविमन्तरेण (दानवीर शिवि के अतिरिक्त)। कः कुर्यात् = कः सम्पादयेत् (कौन करे)।

सन्दर्भ-प्रसङ्गश्च – यह नाट्यांश हमारी शेमुषी पाठ्य-पुस्तक के ‘प्राणेभ्योऽपि प्रियः सुहृद्’ पाठ से लिया गया है। मूलतः यह पाठ महाकवि विशाखदत्त रचित नाटक ‘मुद्राराक्षसम्’ नाटक के प्रथम अंक से सङ्कलित किया गया है। इस अंश में चाणक्य और चन्दनदास का संवाद विवाद में परिवर्तित हो जाता है।

हिन्दी-अनुवादः :

• चाणक्य – तो अब कहाँ गए ?
• चन्दनदास – मैं नहीं जानता (मुझे पता नहीं)।
• चाणक्य – क्यों नहीं जानते हो। अरे सेठजी, डर तो सिर पर सवार है और (उसका) उपाय बहुत दूर है।
• चन्दनदास – आर्य ! क्या मुझे डरा रहे हैं ? घर में होते हुए भी अमात्य राक्षस के परिवार के लोगों को नहीं दे सकता हूँ फिर न होने पर तो कहना ही क्या ?
• चाणक्य – चन्दनदास ! क्या तुम्हारा यही निश्चय है ?
• चन्दनदास – हाँ, मेरा यही निश्चय है।
• चाणक्य – (मन ही मन) धन्य हो चन्दनदास, तुम धन्य हो।
  दूसरे की वस्तु को समर्पित करने पर धन की प्राप्ति आसान हो जाने पर भी यह (स्वार्थ त्यागकर दूसरे की वस्तु की रक्षा करने का) कार्य मनुष्यों में अत्यन्त कठिन कार्य है। दानवीर शिवि के (तुम्हारे) अलावा (अतिरिक्त) इसे और कौन करे।