Jharkhand Board JAC Class 9 Maths Solutions Chapter 7 Triangles Ex 7.4 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.4
Page-132
Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side
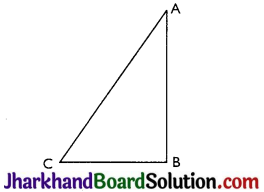
Answer:
ABC is a triangle right angled at B.
Now,
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠C = 90° (∵ ∠B = 90°)
So ∠A < 90° and ∠C < 90°
⇒ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB [As side opposite to larger angle is longer]
Question 2.
In Fig, sides AB and AC of AABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
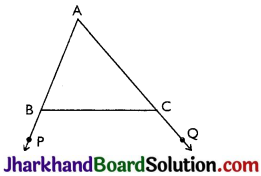
Answer:
Given: ∠PBC < ∠QCB
Proof: ∠ABC + ∠PBC = 180°
⇒ ∠PBC = 180° – ∠ABC …(i)
Also, ∠ACB + ∠QCB = 180°
⇒ ∠QCB = 180° -∠ACB
⇒ ∠PBC < ∠QCB (Given)
⇒ 180° – ∠ABC < 180° – ∠ACB
(From (i) and (ii))
⇒ – ∠ABC < – ∠ACB
⇒ ∠ABC > ∠ACB
⇒ AC > AB (As sides opposite to larger angle is longer.)
![]()
Question 3.
In Fig, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
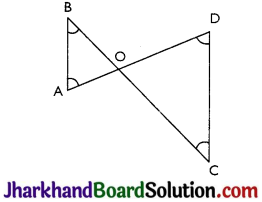
Answer:
Given: ∠B < ∠A and ∠C < ∠D
Proof: In ΔAOB,
∠B < ∠A ⇒ AO < BO ……….(i)
(Side opposite to smaller angle is smaller)
In ΔCOD
∠C < ∠D ⇒ DO < CO…(ii)
(Side opposite to smaller angle is smaller)
Adding (i) and (ii)
AO + OD < BO + OC
⇒ AD < BC
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig). Show that ∠A > ∠C and ∠B > ∠D.
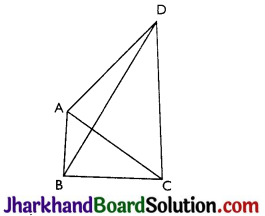
Answer:
In ΔABD,
AB < AD (As AB is the shortest side)
∴ ∠ADB < ∠ABD ……..(i) (Angle opposite to longer side is larger.)
Now, in ΔBCD,
BC < DC (As CD is the longest side)
∴ ∠BDC < ∠CBD …..(ii) (Angle opposite to longer side is larger.)
Adding (i) and (ii), we get
∠ADB + ∠BDC < ∠ABD + ∠CBD
⇒ ∠ADC < ∠ABC
⇒ ∠B > ∠D
Similarly, in Δ ABC,
AB < BC (As AB is the smallest side)
∠ACB < ∠B AC …(iii) (Angle opposite to longer side is larger)
Now, in ΔADC,
AD < DC (As CD is the longest side)
∠DCA < ∠DAC …(iv) (Angle opposite to longer side is larger)
Adding (iii) and (iv), we get
∠ACB + ∠DCA < ∠BAC + ∠DAC
⇒ ∠BCD < ∠BAD
⇒ ∠A > ∠C
Question 5.
In Fig, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ
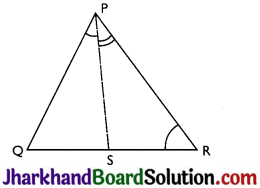
Answer:
Given: PR > PQ and PS bisects ∠QPR
To prove: ∠PSR > ∠PSQ
Proof: ∠PQR > ∠PRQ …….(i)
(PR > PQ as angle opposite to longer side is larger)
∠QPS = ∠RPS …(ii) (PSbisects ∠QPR)
∠PSR = ∠PQR + ∠QPS ………(iii)
(exterior angle of a triangle equals the sum of opposite interior angles)
∠PSQ = ∠PRQ + ∠RPS …(iv)
(exterior angle of a triangle equals the sum of opposite interior angles)
Adding (i) and (ii)
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [from (iii) and (iv)]
![]()
Page-133
Question 6.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
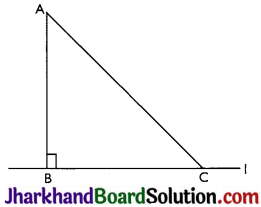
Answer:
Given: Let l is a line segment and B is a point lying on it. We draw a line segment AB perpendicular to 1. Let C be any other point on 1.
To prove: AB < AC
Proof: In ∆ABC,
∠B = 90°
Now, ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒ ∠C < 90° (∠B = 90°)
⇒ ∠C < ∠B
∴ ∠C must be acute angle or ∠C < ∠B
⇒ AB < AC (Side opposite to the larger angle is longer.)