Month: February 2023

Jharkhand Board JAC Class 10 Science Important Questions Chapter 5 Periodic Classification of Elements Important Questions and Answers.

JAC Board Class 10 Science Important Questions Chapter 5 Periodic Classification of Elements

Additional Questions and Answers

Question 1.
Answer the following questions in short:
(1) From the following elements :
20^Ca, 3^Li, 11^Na, 10^Ne
(a) Select the element which has two shells, both of which are completely filled with electrons.
(b) Select two elements of the same group.
Answer:
(a) Element in which two shells are completely filled with electrons is 10^Ne (2, 8).
(b) Two elements of the same group are 3^Li(2, 1) and 11^Na (2, 8, 1).

(2) Answer the following questions [for an element having atomic number 17] :
(a) Name the element.
(b) In which period will you find this element?
(c) To which group of the periodic table does this element belong?
(d) State the electronic configuration of the element.
Answer:
(a) Chlorine
(b) Third period
(c) Group 17
(d) Electronic configuration : 2, 8, 7

(3) An element X (atomic number 17) reacts with an element Y (atomic number 20) to form a divalent halide.
(a) What is the position of elements X and Y in the periodic table?
(b) What will be the nature of oxide of element Y? Identify the nature of bonding in the compound formed.
Answer:
Element X is a non-metal while element Y is a metal.
Molecular formula of dihalide is YX₂.
(a)

Position	Element X	Element Y
In a group	17	2
In a period	3	4

(b) Basic oxide : YO
Nature of the bond : Ionic

(4) Two elements M and N belong to the same period of the modern periodic table and are in group I and group II respectively. Compare their following properties:
(a) Atomic size
(b) Metallic character
(c) Valency of oxides
(d) Molecular formula of their chlorides
Answer:
(a) Element ‘M’ has larger atomic size than that of ‘N’.
(b) Element ‘M’ possess more metallic? character than that of ‘N’.
(c) Group I : Valency : 1
Group II : Valency : 2
(d) MCl, MCl₂

(5) A part of the periodic table has been shown below :

Answer the following questions on the basis of position of elements in the above table:
(a) Which element is a noble gas? Give reason.
(b) Which element is most electronegative? Give reason.
(c) Write the electronic configuration of B and E.
Answer:
(a Element G is a noble gas, because it is present in group 18 and has zero valency.
(b) Element E is the most electronegative element due to its small size and greater tendency to gain electrons.
(c) Electronic configuration of ‘B’ = 2,8, 1 Electronic configuration of ‘E’ = 2, 7

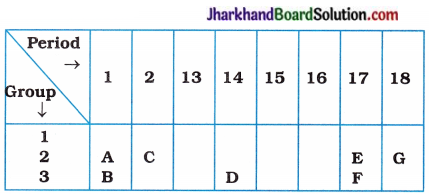
(6) The positions of elements A, B, C, D, E, F, G and H in their respective groups are as follows :

Group	1	2	13	14	15	16	17	18
Element	A	B	C	D	E	F	G	H

Answer the following questions:
(a) Which elements have the largest and smallest atomic size?
(b) Which elements have the valency 3 and 0 respectively?
Answer:
(a) Largest atomic size : A
Smallest atomic size : G
(b) Valency 3 : Element C
Valency O : Element H

(7) Consider the part of periodic table given below and answer the following questions :

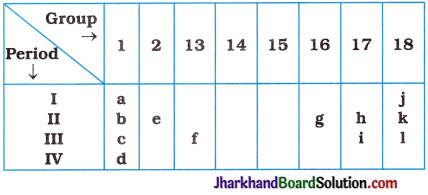
(i) State the most reactive metal.
(ii) How many shells does element d have?
(iii) Identify the element having valency 2.
(iv) Write the number of electrons in the valence shell of j.
(v) Out of h and i, which element is more non-metallic in nature?
(vi) Out of e and h, which element possess large atomic size?
Answer:
(i) d
(ii) 4
(iii) e and g
(iv) 2
(v) h
(vi) e

(8)

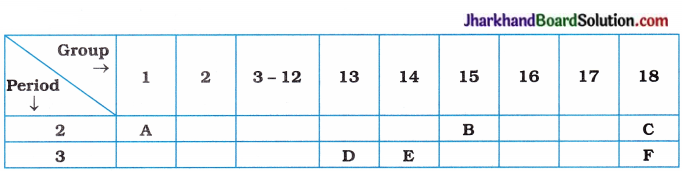
Using the above table, answer the following questions:
(i) Which element will form only covalent compounds?
(ii) Which element is a metal with valency 3?
(iii) Which element is a non-metal with valency 3?
(iv) Out of D and E, which one has a bigger atomic size?
(v) Write common name for the family of elements, C and F.
Answer:
(i) E
(ii) D
(iii) B
(iv) D
(v) Inert gases or noble gases

Question 2.
Distinguish between the following :
(1) Elements of a group and Elements of a period
Answer:

Elements of a group	Elements of a period
1. The atomic number of elements increases on moving down the group.	1. The atomic number of elements increases on moving from left to right along a period.
2. All the elements in a group have same number of valence electrons.	2. The number of valence electrons of the elements in a period increases.
3. The chemical reactivity of elements in a group are same or identical.	3. The chemical reactivity of elements in a period are not identical.
4. The atomic radius and metallic character increase on moving down the group.	4. The atomic radius and metallic character decrease on moving from left to right along a period.

(2) Mendeleev’s periodic table and the Modern periodic table
Answer:

Mendeleev’s periodic table	Modern periodic table
1. Mendeleev’s periodic table consists of seven periods and eight groups.	1. Modern periodic table consists of seven periods and eighteen groups.
2. Transition elements are not separated in the Mendeleev’s periodic table.	2. Transition elements are placed in a separate groups in the modern periodic table.
3. In Mendeleev’s periodic table, elements are arranged in increasing order of their atomic masses.	3. In the modern periodic table, elements are arranged in increasing order of their atomic numbers.
4. Period number and group number of an element cannot be predicted.	4. Period number and group number of an element can be determined easily.
5. Mendeleev’s periodic table has descripancies and limitations.	5. Modern periodic table is almost errorless.
6. Periodicity in the properties of elements cannot be explained.	6. Periodicity in the properties of elements can be explained.

(3) Metallic elements and Non-metallic elements
Answer:

Metallic elements	Non-metallic elements
1. They are electropositive elements.	1. They are electronegative elements.
2. Metals have tendency of losing the electrons during the bond formation process.	2. Non-metals have tendency of gaining the electrons during the bond formation process.
3. Oxides of metals are basic.	3. Oxides of non-metals are acidic.
4. Metals possess 1, 2 or 3 electrons in their respective valence shells.	4. Non-metals possess 5, 6 or 7 electrons in their respective valence shells.

Question 3.
Give scientific reasons for the following statements:
(1) Dobereiner’s triads could not arrange all the elements known at that time.
Answer:
In Dobereiner’s triads, three elements were arranged in the order of increasing atomic masses of elements in which the atomic mass of the middle element is the average of the atomic masses of the other two elements.

Dobereiner could identify triads from the elements known at that time was only a coincidence. Thus, this classification of elements into triads could not be applied to all the elements known at that time.

(2) Newlands’ law of octaves could not classify all the elements known at that time.
Answer:
Newlands’ law of octaves was applicable upto calcium. After calcium, every eighth element s did not possess properties similar to that of the first element.

• Newlands’ assumed that only 56 elements existed s in nature.
• Newlands’ law of octaves was found correct only to lighter elements.
• Thus, all the elements could not be classified s by the Newlands’ law of octaves.

(3) No fixed position can be assigned to hydrogen in the periodic table.
Answer:
Electronic configuration of hydrogen resembles with alkali metals.

• Like alkali metals, hydrogen combines with halogens, oxygen and sulphur to form compounds having similar formulae.
• Hydrogen also resembles halogens as it exists in the form of diatomic molecules.
• Hydrogen combines with metals and non-metals to form ionic and covalent bonds respectively.
• Thus, hydrogen cannot be assigned fixed position in the periodic table.

(4) The atomic size decreases in a period on moving from left to right.
Answer:
As moving from left to right in a period, the atomic number of elements increases by 1.

• As atomic number increases, nuclear charge also increases.
• Due to this increased nuclear charge, the electrons are attracted strongly towards the nucleus and hence the atomic size decreases.

(5) On moving down in a group, the atomic radii of elements increases gradually.
Answer:
On moving down in a group, the atomic number of element increases.

• A new shell of electrons is added with increase in atomic numbers of elements.
• Thus, the distance between the valence shell and nucleus increases and atomic size increases down the group inspite of the increase in nuclear charge.

Objective Questions and Answers

Question 1.
Answer the following questions in one word:

1. How many elements are known till date?
2. How many amongst the known elements are naturally occurring?
3. In which two types the elements were classified in early attempts?
4. By which name the law proposed by Dobereiner is known?
5. How many elements were classified by Dobereiner’s triads?
6. Cl, X and I are the elements of Dobereiner’s triad, then what would be the element X?
7. Name the elements Newlands started and ended the classification of elements.
8. With what Newlands’ law of octaves was compared?
9. Name the element having similar property with lithium in Newlands’ law of octaves.
10. Which element possess similar property with boron in Newlands’ law of octaves?
11. Name two elements which were placed in the same slot in Newlands’ octaves.
12. How many elements were known when Mendeleev started the classification of elements?
13. Name two elements which formed compound on which Mendeleev had concentrated.
14. What are the vertical columns and the horizontal rows called in Mendeleev’s periodic table?
15. Which Sanskrit prefix was used by Mendeleev in the naming of elements which were not discovered at that time?
16. Which element was not placed in Mendeleev’s periodic table properly?
17. Which scientist proposed tire ‘periodic law’ for the modern periodic table?
18. Write the number of elements present in first, third and fourth period in the modern periodic table.
19. State the number of elements present in sixth period of the modern periodic table.
20. How many groups are present in the modern periodic table?
21. How many elements exist as gases in the modern periodic table?
22. By what names the elements of group I are known in the modern periodic table?
23. By which formula the maximum number of electrons that can be accommodated in a shell determines?
24. Write the valency of an element having atomic number 13.
25. Name the elements in the modern periodic table having lowest and highest atomic radii.
26. State the radius of a hydrogen atom.

Answer:

1. 118
2. 98
3. Metals and non-metals
4. Law of Triads
5. 9
6. Br
7. Hydrogen and thorium
8. Indian musical notes
9. Sodium
10. Aluminium
11. Cobalt and nickel
12. 63
13. Hydrogen and oxygen
14. Groups and periods
15. Eka
16. Hydrogen
17. Henry Moseley
18. 2, 8, 18
19. 32
20. 18
21. 11
22. Alkali metals
23. 2n²
24. 3
25. He and Fr
26. 39

Question 2.
Define :
(1) Isotopes
Answer:
Atoms of the same element having same atomic number but different atomic masses are known as isotopes.

(2) Periodic properties
Answer:
Properties of the elements which are periodic function of their electronic configuration and are repeated after definite interval of atomic numbers.
OR
Properties which show the regular gradation in the same group (moving from top to bottom) or along a period (moving from left to right) are known as periodic properties.

(3) Valency
Answer:
The valency is the combining capacity of an atom of an element to acquire noble gas configuration.

(4) Atomic radius
Answer:
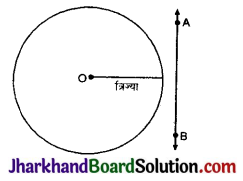
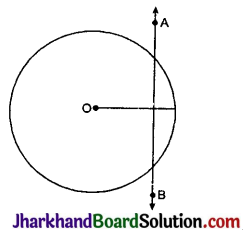
The distance between the centre of the nucleus and the outermost shell of an isolated atom is called atomic radius.

(5) Metalloids (Semi-metal)
Answer:
Elements which possess intermediate properties of both metals and non-metals are called metalloids or semi-metals.

Question 3.
Fill in the blanks :

1. Lithium, sodium and …………………. are the members of Dobereiner’s triad.
2. Newlands’ law of octaves is applicable for …………………. elements.
3. According to Newlands, …………………. elements occur in nature.
4. Mendeleev named scandium as ………………….
5. The element known as eka-silicon is ………………….
6. The position of cobalt in Mendeleev’s periodic table is prior to ………………….
7. If the valency of an element is 2, then it lies in group ………………….
8. The electronic configuration of an element is 2, 8, 3, then it is an element of …………………. period.
9. In the modern periodic table, noble gases are placed in group ………………….
10. Modern periodic table consists of …………………. periods and …………………. groups.
11. Position of …………………. in the periodic table is controversial.
12. The valency of noble gases is ………………….
13. On moving down in any group, the metallic character of the elements ………………….
14. Oxides of non-metallic elements are …………………. in nature.
15. Oxides of …………………. elements are basic in nature.

Answer:

1. potassium
2. lighter
3. 56
4. eka-boron
5. germanium
6. nickel
7. 2
8. third
9. 18
10. 7, 18
11. hydrogen
12. zero
13. increases
14. acidic
15. metallic

Question 4.
State whether the following statements are true or false:

1. At present, naturally occurring elements are 98.
2. The atomic masses of elements form a Dobereiner’s triad are 14 u, 31 u and 74.9 u respectively.
3. Calcium, strontium and barium form a Dobereiner’s triad.
4. According to the Newlands’ law of octaves, every eighth element had properties similar to that of the first element.
5. Sodium is the eighth element after lithium.
6. Oxygen is the eighth element after sulphur.
7. Phosphorus is tire eighth element after nitrogen.
8. Dobereiner’s triads are observed in Newlands’ octaves.
9. Mendeleev’s periodic law was based on atomic number of element.
10. Molecular formula of oxide of barium is BaO.
11. Mendeleev named gallium for eka-silicon.
12. An element having atomic number 3.5 can be placed between Be and B.
13. There are three valence electrons present in the elements of group I.
14. Electrons are filled in K, L and M shells in the elements of the third period.
15. Each period starts with the filling of electrons in a new shell.

Answer:

1. True
2. False
3. True
4. True
5. True
6. False
7. False
8. True
9. False
10. True
11. False
12. False
13. False
14. True
15. True

Question 5.
Match the following properly :
(1)

Column I	Column II
1. Dobereiner	a. Law of octaves
2. Newlands	b. Periodic law
3. Mendeleev	c. Modern periodic table
4. Henry Moseley	d. Law of triads

Answer:
(1-d), (2-a), (3- b), (4 – c).

(2)

Column I	Column II
1. Li, Na, K	a. Metalloids
2. S, E Cl	b. Noble gases
3. B, Si, Ge	c. Non-metallic elements
4. He, Ne, Ar	d. Metallic elements

Answer:
(1-d), (2-c), (3-a), (4-b).

Question 6.
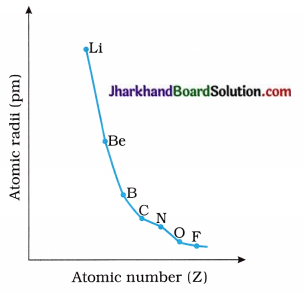
Draw the following graphs :
1. Draw the graph of Atomic radii → Atomic numbers for the elements of second period.
Answer:

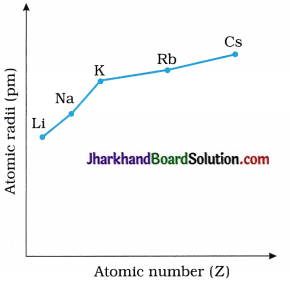
2. Draw the graph of Atomic radii → Atomic numbers for the alkali metal elements.
Answer:

Question 7.
Which one of the following depict the correct representation of atomic radius of an atom?

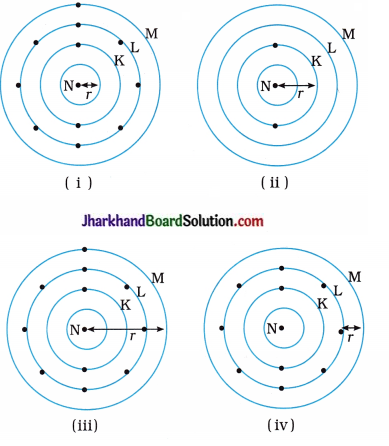
Answer:
(ii) and (iii)

Question 8.
(A) Choose the correct option from those given below each question:
1. For which of the following element, Mendeleev didn’t left gap in his periodic table?
A. Gallium
B. Beryllium
C. Germanium
D. Scandium
Answer:
B. Beryllium

2. Newlands’ law of octaves was found to be applicable upto …………………
A. nickel
B. cobalt
C. phosphorus
D. calcium
Answer:
D. calcium

3. According to Mendeleev’s periodic law, the elements were arranged in the periodic table in the order of…
A. increasing atomic number.
B. decreasing atomic number.
C. increasing atomic masses.
D. decreasing atomic masses.
Answer:
C. increasing atomic masses.

4. The elements Si, B and Ge are …………………
A. metallic elements
B. non-metals
C. metalloids
D. metal, non-metal and metalloid respectively
Answer:
C. metalloids

5. In Mendeleev’s periodic table, gaps were left for the elements to be discovered later. Which of the following elements found a place in the periodic table later?
A. Be
B. Ge
C. Si
D. Se
Answer:
B. Ge

6. The three imaginary elements X, Y and Z represent a Dobereiner’s triad. If the atomic mass of element X is 14 u and that of element Y is 46 u, then the atomic mass of element Z will be …………………
A. 28
B. 60
C. 78
D. 72
[Hint: According to the law of Dobereiner’s triad,
Atomic mass of Y

Answer:
C. 78

7. The atomic numbers of four elements R Q, R and S are 6, 8, 14 and 16 respectively. Out of these, the element known as metalloid is ……….
A. P
B. Q
C. R
D. S
[Hint: Elements in which generally four? electrons are present in outermost shell are called metalloids.]
Answer:
C. R

8. Which of the following statements is correct with regard to the classification of elements?
A. Elements in modern periodic table are arranged on the basis of increasing atomic masses.
B. Elements in modern periodic table are arranged on the basis of decreasing atomic numbers.
C. In modern periodic table, the element nickel of lower atomic mass is kept before the element cobalt of higher atomic mass.
D. In modern periodic table, the isotopes of chlorine having different atomic masses are kept in the same group.
Answer:
D. In modern periodic table, the isotopes of chlorine having different atomic masses are kept in the same group.

9. Which of the following statements about the modern periodic table is correct?
A. It has 18 horizontal rows known as periods.
B. It has 8 vertical columns known as periods.
C. It has 18 vertical columns known as groups.
D. It has 7 horizontal rows known as groups.
Answer:
B. It has 8 vertical columns known as periods.

10. An element X forms an oxide X₂O₃. In which : group of Mendeleev’s periodic table is this element placed?
A. Group II
B. Group III
C. Group V
D. Group VIII
Answer:
B. Group III

11. Who proposed the ‘Modern periodic law’ for the modern periodic table?
A. Dobereiner
B. Newlands
C. Henry Moseley
D. Mendeleev
Answer:
C. Henry Moseley

12. Which fundamental particle forms the real basis for the modern classification of elements?
A. Proton
B. Electron
C. Neutron
D. Nucleon
Answer:
A. Proton

13. Which of the following is not correct about the trends when going from left to right across the periods of the periodic table?
A. The elements become more non-metallic in nature.
B. The number of valence electrons increases.
C. The atoms lose their electrons easily.
D. The oxides become more acidic.
Answer:
C. The atoms lose their electrons easily.

14. The electronic configuration of the atom of an element X is 2, 8, 4. In modern periodic table, the element X is placed in
A. Group 2
B. Group 14
C. Group 4
D. Group 8
Answer:
B. Group 14

15. The atomic number of an element is 20. In modern periodic table, this element is placed in ……………..
A. 2nd period
B. 3rd period
C. 1st period
D. 4th period
Answer:
D. 4th period

16. The elements A, B, C, D and E have atomic numbers of 2, 3, 7, 10 and 18 respectively. The elements which belong to the same period of the periodic table are
A. A, B, C
B. B, C, D
C. A, D, E
D. B. D, E
Answer:
B. B, C, D

17. The elements A, B, C, D and E have atomic numbers 9, 11, 17, 12 and 13 respectively. The pair of elements which belong to the same group of the periodic table is ……………..
A. A and B
B. B and D
C. D and E
D. A and C
Answer:
D. A and C

18. Which of the following element would lose an electron easily?
A. Mg
B. Na
C. K
D. Ca
Answer:
C. K

19. Which of the following element will gain an electron easily?
A. Na
B. F
C. Mg
D. Al
Answer:
B. F

20. Where would you place the element with electronic configuration 2, 8 in the modern periodic table?
A. Group 8
B. Group 2
C. Group 18
D. Group 10
Answer:
C. Group 18

21. An element which is an essential constituent of all organic compounds belong to ……………..
A. Group 4
B. Group 10
C. Group 16
D. Group 14
Answer:
D. Group 14

22. Which of the following is the valence shell for the elements of second period of the modern periodic table?
A. M-shell
B. K-shell
C. N-shell
D. L-shell
Answer:
D. L-shell

23. The element which has the maximum number of valence electrons is ……………..
A. 15^P
B. 11^Na
C. 14^Si
D. 13^Al
Answer:
A. 15^P

24. The correct increasing order of the atomic radii of the elements oxygen, fluorine and nitrogen is ……………..
A. O, F, N
B. N, F, O
C. O, N, F
D. F, O, N
Answer:
D. F, O, N

25. Which one of the following does not increase while moving down the group of the periodic table?
A. Atomic radius
B. Metallic character
C. Valence electrons
D. Basicity of oxides
Answer:
C. Valence electrons

(B) Choose more than one correct options from those given below each question:
1. Mention the drawbacks of Mendeleev’s periodic table.
A. Position of hydrogen
B. Position of isotopes
C. Arrangement of Noble gases
D. Arrangement of more than one elements in the same slot.
Answer:
A, B, C, D

2. Which of the following increase while moving down the group 17 elements?
A. Atomic radius
B. Valence electrons
C. Metallic character
D. Acidity of oxides
Answer:
A, C

3. Which of the following statements are correct for modern periodic table?
A. New elements can be easily arranged.
B. Predictions of properties of the elements become easy.
C. The elements have been divided into metals and non-metals by the thick zig-zag line running diagonally across the periodic table.
D. Atomic volume of elements decreases on moving down in the group.
Answer:
A, B, C

4. The electronic configuration of the atom of an element is 2, 8, 7. In this reference, which of the following statements are correct?
A. This element belong to group 17.
B. This element has a tendency to gain one electron.
C. This element belongs to fourth period.
D. The element fluorine is placed above this element.
Answer:
A, B, D

(C) In each of the following questions, a statement of Assertion A is given, followed by a Reason R. Read the statements carefully and choose the correct option as under:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.
B. Assertion A and reason R are true, but reason R is not the correct explanation of assertion A.
C. Assertion A is corret but reason R is false.
D. Assertion A is false but reason R is true.
1. Assertion A: The position of hydrogen in modern periodic table is a matter of controversy.
Reason R : The properties of hydrogen resembles with the properties of alkali metals and halogens.
Answer:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.

2. Assertion A: In the modern periodic table, metallic character of elements increases on moving down the group.
Reason R: In the modern periodic table, the elements are arranged in order of their increasing atomic masses.
Answer:
C. Assertion A is corret but reason R is false.

3. Assertion A : Newlands arranged the then known elements in order of musical notes.
Reason R: According to Newlands, proton is responsible for the arrangement of elements in the periodic table.
Answer:
C. Assertion A is corret but reason R is false.

4. Assertion A : Chemical reactivity of the element of group 18 is very less.
Reason R : Their outermost shell is completely filled with electrons.
Answer:
A. Assertion A and reason R are true, and reason R is the correct explanation of assertion A.

Value Based Questions With Answers

Question 1.
Six elements of periodic table A, B, C, D, E and F have atomic numbers of 2, 12, 20, S 18, 4 and 10 respectively (where A, B, C,? D, E and F are not the chemical symbols of s these elements). Based on this information, answer the following questions :
(1) Which of these elements belong to the same groups of the periodic table? Why?
(2) Which of these elements belong to the same periods of the periodic table? Why?
(3) Which of these elements are (i) metals and (ii) non-metals?
(4) Which of these elements are chemically (i) reactive and (ii) unreactive?
(5) What values are indicated in a student in answering the above questions?
Answer:
First of all, write the electronic configurations? of all the given six elements as follows :

Element	Atomic number	Electronic configuration
		K	L	M	N
A	2	2
B	12	2	8	2
C	20	2	8	8	2
D	18	2	2	8
E	4	2	8
F	10	2	8

(1) (i) Elements B, C and E belong to the s group 2 of the periodic table because all of them have an equal number of valence electrons equal to 2.

(ii) Elements A, D and F also belong to the group 18 because they are all inert gases having completely filled outermost electron shells with 8 valence electrons.

(2) (i) Element B (2, 8, 2) and element D (2, 8, 8) belong to the third period because they both have 3 electron shells – K, L and M each.

(ii) Element E (2, 2) and element F (2, 8) belong to the second period because they both have 2 electron shells – K and L each.

(3) (i) Elements B, C and E belonging to group 2 are metals.
(ii) Elements A, D and F belonging to group 18 are non-metals (noble gases).

(4) (i) Elements B, C and E of group 2 are chemically reactive elements.
(ii) Elements A, D and F of group 18 are chemically unreactive elements.

(5) Answering these questions by a student are indicating awareness towards modern periodic classification of the elements and ability to apply his knowledge in solving the related questions.

Question 2.
In his periodic table, Mendeleev arranged all the then known 63 elements in the order of increasing atomic masses in horizontal rows but in such a way that elements having similar properties came directly under one another in the same vertical column. In the classification of the then known elements, Mendeleev was guided mainly by two factors.

In order to make sure that the elements having similar properties fall in the same vertical column, Mendeleev left some gaps in his periodic table. Though leaving gaps in the periodic table was considered to be a drawback of his classification of elements at that time but Mendeleev was firm on his decision.
Answer the following questions:
(1) What are the horizontal rows of Mendeleev’s periodic table known as? How many horizontal rows of elements were there in Mendeleev’s periodic table?

(2) What are the vertical columns of Mendeleev’s periodic table known as? How many vertical columns were there? in Mendeleev’s periodic table?

(3) What were the similar properties used by Mendeleev to classify the then known elements into vertical columns?

(4) What were the two main guiding factors for Mendeleev in the classification of the then known elements?

(5) For what purpose were some gaps left by Mendeleev in his periodic table? Does the modern periodic table also have the 5 gaps left by Mendeleev?

(6) What values were displayed by Mendeleev in presenting his classification of elements?
Answer:
(1) The horizontal rows of elements in the Mendeleev’s periodic table are called periods. There were seven periods in s Mendeleev’s periodic table.

(2) The vertical columns of Mendeleev’s periodic table are called groups. There were eight groups in Mendeleev’s periodic s table.

(3) The similar properties used by Mendeleev to classify the elements into vertical columns were the similar formulae of S their oxides and hydrides.

(4) The two main guiding factors for Mendeleev in the classification of the then known elements were

• increasing t order of atomic masses
• grouping together the elements having similar properties.

(5) These gaps were left for the elements which had not been discovered at that time. He thought that these elements would be discovered later in future. The modern periodic table does not have any gaps.

(6) The various values displayed by Mendeleev were-

• self-confidence
• courage
• foresight
• prophecy.

Question 3.
There are three elements X, Y and Z having atomic numbers of 6, 16 and 19 respectively. Based on this information, Het has been asked to answer the following questions :
(1) In which group of the periodic table would you expect to find (i) element X (ii) element Y and (iii) element Z?
(2) Which two elements will form ionic bonds? Why?
(3) What will be the formula of ionic compound formed?
(4) Which two elements will form covalent bonds? Why?
(5) What will be the formula of covalent compound formed?
(6) What values are displayed by Het in answering the above questions?
Answer:
In order to answer these questions, Het first wrote down the electronic configurations of the elements X, Y and Z by using their atomic numbers, as follows :

Element	Atomic number	Electronic configuration
		K	L	M	N
X	6	2	4
Y	16	2	8	6
Z	19	2	8	8	1

(1) (i) Element X has 4 valence electrons in its atom, so it will be placed in group 4 + 10 = 14 of the modern periodic table.
(ii) Element Y has 6 valence electrons in its atom, so it will be placed in group 6 + 10 = 16 of the modern periodic table.
(iii) Element Z has 1 valence electron in its atom, so it will be placed in group 1 of the modern periodic table.

(2) An ionic bond is formed between a metal element and a non-metal element. Here, the elements Z and Y will combine to form ionic bond.

(3) The element Z has 1 valence electron, so its valency is +1 (after losing this electron). The element Y need two electrons to complete its octet. So, element Y will gain two electrons and form Y^2- ion. Here, two Z⁺ ions will combine with one Y^-2 ion, so that the formula of ionic compound formed will be Z₂Y.

(4) A covalent bond is formed between two non-metallic elements. Here, element X of group 14 is a non-metal and element Y of group 16 is also a non-metal. Therefore, the elements X and Y will combine together to form covalent bonds.

(5) The element X has 4 valence electrons, so its valency is 4. The element Y has 6 valence electrons, so its valency is 2. So, one atom of element X will combine with two atoms of element Y to form a covalent compound having the formula XY₂.

(6) The values displayed by Het in answering these questions are (1) knowledge of modern classification of elements, and (2) understanding of periodic table.

Practical Skill Based Questions With Answers

Question 1.
Complete the following cross-word puzzle :

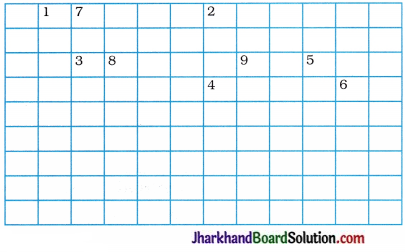
Across:
(1) An element with atomic number 12.
(3) Metal used in making cans and member of group 14.
(4) A lustrous non-metal which has 7 electrons ; in its outermost shell.

Down:
(2) Highly reactive and soft metal which imparts yellow colour when subjected to flame and is kept in kerosene.
(5) The first element of second period.
(6) An element which is used in making fluorescent bulbs and is second member of group 18 in the modern periodic table.
(7) A radioactive element which is the last member of halogen family.
(8) Metal which is an important constituent of steel and forms rust when exposed to moist air.
(9) The first metalloid in modern periodic table whose fibres are used in making bullet-proof vests.
Answer:

Question 2.
In this ladder, symbols of elements are jumbled up.
(a) Rearrange these symbols of elements in the increasing order of their atomic numbers in the periodic table.
(b) Arrange them in the order of their group also.

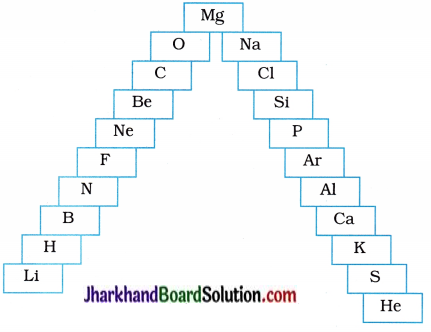
Answer:
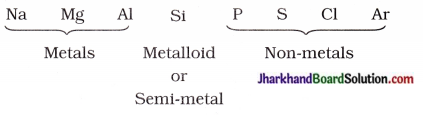
(a) H, He, Li, Be, B, C, N, O, F, Ne, Na, Mg, Al, Si, E S, Cl, Ar, K, Ca.
(b)

Group	Elements
1	H, Li, Na, K
2	Be, Mg, Ca
13	B, Al
14	C, Si
15	N, P
16	O, S
17	F, Cl
18	He, Ne, Ar

Memory Map

Students should go through these JAC Class 10 Maths Notes Chapter 15 प्रायिकता will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 15 प्रायिकता

भूमिका :
कक्षा IX में हमने किसी घटना के प्रायोगिक या अनुभाविक प्रायिकता के बारे में अध्ययन किया था। स्मरण करें जिस प्रायिकता का अनुमापन हम वास्तविक प्रयोगों के परिणामों तथा घटनाओं के घटित होने की पर्याप्त रिकार्डिंग के आधार पर करते हैं, उस प्रायिकता को प्रायोगिक या आनुभाविक प्रायिकता कहते हैं।

प्रायिता-एक सैद्धान्तिक दृष्टिकोण :
उदाहरण के लिए-जब हम एक सिक्का उछालें तो यह समतल पर गिरेगा। यह एक क्रिया या प्रयोग है जिससे दो परिणाम प्राप्त हो सकते हैं-चित (अशोक वाला) तल दिखायी दे अथवा पट (दूसरा तल) दिखायी दे ये दो सम्भव घटनाएँ (Events) हैं।
(i) इस प्रकार हम देखते हैं कि सिक्का उछालने के किसी प्रयोग में कुल सम्भावित घटनाएँ दो हैं चित गिरने की सम्भावना 2 घटनाओं में से 1 है और पट गिरने की सम्भावना भी उतनी ही है। तब गणित की भाषा में हम कहते हैं कि सिक्के के चित गिरने की प्रायिकता \(\frac{1}{2}\) है। सिक्के के पट गिरने की भी प्रायिकता \(\frac{1}{2}\) है।

(ii) किसी चुनाव में A, B, C, D चार उम्मीदवार खड़े हैं, तब सफल प्रत्याशी के चुनाव की कुल 4 सम्भावनाएँ हैं, क्योंकि चारों प्रत्याशियों में से कोई भी सफल हो सकता है, तब प्रत्याशी A की सफलता की सम्भावना 4 में से 1 है।
हम गणित की भाषा में कह सकते हैं कि प्रत्याशी A की सफलता की प्रायिकता \(\frac{1}{4}\) है; शेष प्रत्याशियों B, C व D की सफलता की भी प्रायिकता उतनी ही है। यहाँ हम कह सकते हैं कि किसी प्रत्याशी की असफलता की प्रायिकता है क्योंकि एक प्रत्याशी के सफल होने की दशा में शेष 3 के असफल होने की घटना अवश्य घटित होगी।

(iii) ताश की गड्डी में से पत्ता खींचिए। इसके लाल होने की प्रायिकता पर विचार कीजिए। कुल 52 पत्तों की गड्डी में 26 लाल और 26 काले पत्ते होंगे, तब पत्ते के लाल होने की प्रायिकता \(\frac{26}{52}\) या \(\frac{1}{2}\) है। खींचे गए पत्ते के लाल न होने की भी प्रायिकता \(\frac{26}{52}\)या \(\frac{1}{2}\) ही है।
→ प्रायिकता (Probability) : जब किसी घटना के घटित होने की सम्भावना संख्यात्मक रूप में व्यक्त की जाती है तो उसे प्रायिकता कहते हैं।

→ प्रयोग (Experiment) : वह विधि जिसके द्वारा हमें किसी प्रेक्षण का परिणाम प्राप्त होता है प्रयोग कहलाता है।

→ परिणाम (Outcome) : किसी प्रयोग के विशिष्ट निष्कर्ष को परिणाम कहते हैं।

→ यादृच्छया प्रयोग (Random Experiment) : ऐसे प्रयोग जिनके निश्चित परिणाम नहीं हों यादृच्छया प्रयोग कहलाते हैं।

→ अभिप्रयोग (Trial) : किसी भी यादृच्छिक प्रयोग को करने की प्रक्रिया को एक अभिप्रयोग (trial) कहते है।

→ पूरक घटनाएँ (Complimentary events) : यदि ‘E’ किसी घटना के घटित होने की प्रायिकता है तथा ‘E नहीं’ न घटित होने की प्रायिकता है तब E और ‘E नहीं’ पूरक घटनाएँ कहलाती हैं।
∴ P(E) + P(E नहीं) = 1.

→ मिश्रित घटनाएँ (Compound events ) : किसी यादृच्छिक प्रयोग से जुड़ी ऐसी घटनाएँ जो दो या दो से अधिक प्रारम्भिक घटनाओं के मिश्रण से प्राप्त होती हैं, मिश्रित घटनाएँ कहलाती हैं।

→ अनुकूल प्रारंभिक घटना (Favourable elementary event) एक ऐसी प्रारम्भिक घटना जो किसी मिश्रित घटना के अनुकूल हो अनुकूल प्रारम्भिक घटना कहते हैं।

→ पासा (Dice or die) : एक छोटा घन जिसके पृष्ठों पर 1 से 6 तक संख्याएँ लिखी हों पासा कहलाता है। प्रायिकता एक सैद्धान्तिक दृष्टिकोण

→ यादृच्छया उछाल (Random toss) : किसी सिक्के को बिना किसी पक्षपात (bias) या रुकावट के स्वतन्त्रता पूर्वक गिरने दिया जाता है तो उसे यादृच्छया उछाल कहते हैं।

→ समप्रायिक (Equally likely) जब किसी यादृच्छया प्रयोग में किसी घटना E के सभी परिणामों के प्राप्त होने की सम्भावना समान होती है तो यह परिणाम समप्रायिक कहलाते हैं।
जैसे- किसी सिक्के को उछालने में चित या पट आना अथवा पाँसे की उछाल में पासे पर अंकित अंकों में से कोई अंक प्राप्त होने की घटना समप्रायिक घटनाएँ हैं।

→ सैद्धान्तिक प्रायिकता (Theoretical Probability) किसी प्रयोग में यदि एक घटना E घटित होती है और यह कल्पना करने पर प्रयोग में घटना E के सभी परिणाम बिल्कुल एक हों तो.

इस प्रकार से अवकलित प्रायिकता को सैद्धान्तिक प्रायिकता कहते हैं।

→ प्रारम्भिक घटना (Elementary event) : वह घटना है जिसका केवल एक ही परिणाम है। किसी पासे को उछालने पर 5 प्राप्त होना प्रारम्भिक घटना है क्योंकि 5 प्राप्त होने का केवल एक ही परिणाम है।
परन्तु विषम या सम संख्या प्राप्त होना प्रारम्भिक घटना नहीं है क्योंकि विषम संख्या प्राप्त होने की घटना के 1, 3, 5 तीन परिणाम हैं। ऐसे ही सम संख्या या 5 से छोटी संख्या प्राप्त होने की घटना भी प्रारम्भिक घटना नहीं है क्योंकि इनके परिणाम 1 से अधिक हैं।
किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्राथकिताओं का योग होता है।

→ असम्भव घटना (Impossible event) : ऐसी घटना जिसकी प्रायिकता शून्य होती है अर्थात् उस घटना का घटित होना असम्भव हो तो उस घटना को असम्भव घटना (Impossible Event) कहते हैं।
किसी पासे की उछाल में “6 से बड़ा अंक प्राप्त होने की घटना” असम्भव घटना है।

→ निश्चित घटना (Sure event) यदि किसी घटना की प्रायिकता हो तो उस घटना को निश्चित घटना (Sure event) कहते हैं।
जैसे-किसी पासे की फेंक में 7 से छोटी संख्या प्राप्त होने की घटना के सभी परिणाम 1, 2, 3, 4, 5, 6 सम्भव हैं। यह एक निश्चित घटना है।

→ घटना (E) घटित नहीं हो : इसे E1 या \(\bar{E}\) से व्यक्त करते हैं तथा घटना को “E नहीं” से जाना जाता है। यदि किसी घटना की प्रायिकता सदैव शून्य के बराबर या उससे अधिक तथा के बराबर या उससे कम होती है।
0 ≤ P(E) ≤ 1

ताश के पत्ते (Playing Cards) :
ताश की गड्डी में कुल पत्तों की संख्या = 52
कुल पत्ते 4 समूहों में विभाजित होते हैं-
(1) हुकुम (Spades), (2) पान (Hearts), (3) ईट (Diamonds), (4) चिड़ी (Clubs)

प्रत्येक समूह में तेरह पत्ते होते हैं अर्थात्
हुकुम के 13, पान के 13, ईंट के 13 और चिड़ी के 13 पत्ते होते हैं।
काले रंग के पत्ते : हुकुम 13 व चिड़ी 13 = कुल 26
लाल रंग के पत्ते : पान 13 व ईंट 13 = कुल 26
प्रत्येक समूह में इक्का (ace), बादशाह (king), बेगम (queen) और गुलाम (jack) उच्च क्रम के पत्ते होते हैं। इक्का (ace) पहले क्रम का पत्ता है और बादशाह (king), बेगम (queen) तथा गुलाम (jack) फेस पत्ते (face cards) कहलाते हैं।

ध्यान देने योग्य बिन्दु :

उक्त प्रकार से अवकलित प्रायिकता को सैद्धान्तिक प्रायिकता कहते हैं।
→ किसी प्रयोग की सभी प्रारम्भिक घटनाओं की प्रायिकता का योग 1 है। यह व्यापक रूप में भी सत्य है।
→ व्यापक रूप में किसी घटना E के लिए सत्य है कि P(\(\bar{E}\)) = 1 – P(E)
→ एक निश्चित या निर्धारित घटना की प्रायिकता 1 होती है।
→ एक असम्भव घटना की प्रायिकता 0 होती है।
→ घटना E की प्रायिकता एक ऐसी संख्या है, कि (PE)
0 ≤ P(E) ≤ 1
→ किसी भी घटना E के लिए P(E) + P(\(\bar{E}\)) = 1 होता है।
जहाँ \(\bar{E}\) घटना ‘E नहीं’ को व्यक्त करता है। E और \(\bar{E}\) पूरक घटनाएँ कहलाती हैं।
→ एक असम्भव घटना की प्रायिकता 0 (या 0%) होती है। जैसे-सूर्य के कभी अस्त नहीं होने की प्रायिकता 0 है।

Jharkhand Board JAC Class 10 Science Solutions Chapter 5 Periodic Classification of Elements Textbook Exercise Questions and Answers.

JAC Board Class 10 Science Solutions Chapter 5 Periodic Classification of Elements

Jharkhand Board Class 10 Science Periodic Classification of Elements Textbook Questions and Answers

Question 1.
Which of the following statements is not a correct statement about the trends when going from left to right across the periods of periodic table :
(a) The elements become less metallic in nature.
(b) The number of valence electrons increases.
(c) The atoms lose their electrons more easily.
(d) The oxides become more acidic.
Answer:
The atoms lose their electrons more easily.

Question 2.
Element X forms a chloride with the formula XCl₂, which is a solid with a high melting point. X would most likely be in the same group of the periodic table as…
(a) Na
(b) Mg
(c) Al
(d) Si
Answer:
Mg

Question 3.
Which element has
(a) two shells, both of which are completely filled with electrons?
(b) the electronic configuration 2, 8, 2?
(c) a total of three shells, with four electrons in its valence shell?
(d) a total of two shells, with three electrons in its valence shell?
(e) twice as many electrons in its second? shell as in its first shell?
Answer:
(a) Neon (2, 8)
(b) Magnesium (2, 8, 2)
(c) Silicon (2, 8, 4)
(d) Boron (2, 3)
(e) Carbon (2, 4)

Question 4.
(a) What property do all elements in the same column of the periodic table as boron have in common?
(b) What property do all elements in the same column of the periodic table as fluorine have in common?
Answer:
(a) In the modern periodic table, Boron is an element of group 13. Its valency is 3. Thus, all other elements of this group have valency 3.

(b) In the modern periodic table, fluorine is an element of group 17. All the elements of this group have 7 electrons in their valence shells. Therefore, the valency of all elements of this group is 1.

Question 5.
An atom has electronic configuration 2, 8, 7.
(a) What is the atomic number of this element?
(b) To which of the following elements would it be chemically similar? (Atomic numbers are given in parentheses.)
N (7) F (9) P (15) Ar (18)
Answer:
(a) The atomic number of this element is 17(2 + 8 + 7).
(b) F (9) [ ∵ Electronic configuration of F is 2, 7.]

Question 6.
The position of three elements A, B and C in the periodic table are shown below:

Group	Group 17
–	–
–	A
–	–
B	C

(a) State whether A is a metal or non-metal.
(b) State whether C is more reactive or less reactive than A.
(c) Will C be larger or smaller in size than B?
(d) Which type of ion, cation or anion, will be formed by element A?
Answer:
(a) Element A is an element of group 17. There are 7 electrons in their valence shell and thus by gaining one more electron it acquire a complete octet. Thus, an element A is a non-metal.

(b) On going down in a group, the atomic s size increases. Therefore, the force of attraction of the nucleus on the incoming electron decreases. As a result, reactivity decreases down the group. Since element C has larger atomic size than A, the element C is less reactive than the element A. In reference of forming positive ion, element C is more reactive than the element A.

(c) Elements B and C belong to the same period. On moving left to right in a period, atomic size (volume) decreases. Thus, the atomic size of C is smaller than B.

(d) Since element A has 7 electrons in the valence shell, it has a tendency to gain one electron to complete its octet. Thus, element A forms an anion.
A + \(\overline{\mathrm{e}}\) → A^–

Question 7.
Nitrogen (atomic number 7) and phosphorus (atomic number 15) belong to group 15 of the periodic table. Write the electronic configuration of these two elements. Which of these will be more electronegative? Why?
Answer:
The electronic configuration of nitrogen and phosphorus are as follows:

Element	Atomic number	Electronic configuration
		K	L	M
Nitrogen (N)	7	2	5	–
Phosphorus (P)	15	2	8	5

Nitrogen is more electronegative than phosphorus because electronegative character decreases on moving down a group.

Question 8.
How does the electronic configuration of an atom relate to its position in the modern periodic table?
Answer:
In the periodic table, position of an element depends on its electronic configuration. The position of an element can be determined by knowing the number of valence electron in its electronic configuration.
For example,

Possesses one electron in its valence shell. Hence, it belongs to group 1.
→ The number of shells in the electronic configuration of an element determines its position in a period.
For example,

has three shells (K, L and M). So, it belongs to 3rd period of the periodic table.

Question 9.
In the modern periodic table, calcium (atomic number 20) is surrounded by elements with atomic numbers 12, 19, 21 and 38. Which of these have physical and chemical properties resembling calcium?
Answer:

Element	Atomic number	Electronic configuration
		k	L	M	N	O
Calcium	20	2	8	8	2	–
Magnesium	12	2	8	2	–	–
Potassium	19	2	8	8	1	–
Scandium	21	2	8	8	3	–
Strontium	38	2	8	18	8	–

Elements with atomic number 12 and 38 have 2 electrons in their last shell like calcium. So, they will resemble Ca in their chemical properties.

Question 10.
Compare and contrast the arrangement of elements in Mendeleev’s periodic table and the modern periodic table.
Answer:

Mendeleev’s periodic table	Modern periodic table
1. Mendeleev’s periodic table consists of seven periods and eight groups.	1. Modern periodic table consists of seven periods and eighteen groups.
2. Transition elements are not separated in the Mendeleev’s periodic table.	2. Transition elements are placed in a separate groups in the modern periodic table.
3. In Mendeleev’s periodic table, elements are arranged in increasing order of their atomic masses.	3. In the modern periodic table, elements are arranged in increasing order of their atomic numbers.
4. Period number and group number of an element cannot be predicted.	4. Period number and group number of an element can be determined easily.
5. Mendeleev’s periodic table has descripancies and limitations.	5. Modern periodic table is almost errorless.
6. Periodicity in the properties of elements cannot be explained.	6. Periodicity in the properties of elements can be explained.

Jharkhand Board Class 10 Science Periodic Classification of Elements InText Questions and Answers

Question 1.
Did Dobereiner’s triads also exist in the columns of Newlands’ octaves? Compare and find out.
Answer:
Dobereiner’s triads also exist in the columns of Newlands’ octaves.

• Lithium, sodium and potassium forms a Dobereiner’s triad.
• Lithium, the first element of this triad is considered as the first element as Newlands’ octave, then the eighth element from it is sodium. These elements possesses similar properties according to the law of triads and the law of octaves.
• Similarly, if sodium is considered as the first element then the eighth element from it is potassium.  Moreover, sodium and potassium possess similar properties according to both the laws.
• Apart from these, some other elements beryllium (Be), magnesium (Mg) and calcium (Ca) obeys law of triads and the law of octaves.
• Thus, Dobereiner’s triads also exist in the columns of Newlands’ octaves.

Question 2.
What were the limitations of Dobereiner’s classification?
Answer:
The limitations of Dobereiner’s classification are as follows:

• All the elements known at that time could not be arranged as Dobereiner’s triad. Hence this method of classification of elements into triads was not found to be successful.
• Three elements nitrogen (N), phosphorus (P) and arsenic (As) were then known elements, but these elements could not be classified as Dobereiner’s triad.

Question 3.
What were the limitations of Newlands’ law of octaves?
Answer:

• Newlands’ law of octaves was applicable only to lighter elements having atomic masses up to 40 u.
  The law of octaves was applicable only s upto calcium, because after calcium every eighth element did not possess properties similar to that of the first element.
• Newlands assumed that only 56 elements s existed in nature and no new elements would be discovered in the future. But, later on, several new elements were discovered whose properties did not fit into the law of octaves.
• In order to fit elements into his table, Newlands adjusted two elements in the same slot, but also put some unlike elements under the same column.

For example, cobalt (Co) and nickel S (Ni) are placed in the same slot and these are placed in the same column as fluorine, chlorine and bromine which have very different properties S than these elements. Iron, which resembles cobalt and nickel in properties, has been placed far away from these elements.

Question 4.
Use Mendeleev’s periodic table to predict the formulae for the oxides of the following elements:
K, C, Al, Si, Ba
Answer:

Element	Group number (Valency)	Molecular formula of oxide
K	1	K<sub>2</sub>O
C	4	CO2
Al	3	Al2O3
Si	4	SiO2
Ba	2	BaO

Question 5.
Besides gallium, which other elements have since been discovered that were left by Mendeleev in his periodic table? (any two)
Answer:
Besides gallium, Mendeleev had left gaps for germanium and scandium in his periodic table.

Question 6.
What were the criteria used by Mendeleev in creating his periodic table?
Answer:
The following criteria was used by Mendeleev in creating his periodic table :

• The properties of elements are the periodic function of their atomic masses.
• Elements with similar properties are arranged in the same group.
• The formula of oxides and hydrides formed by an element.

Question 7.
Why do you think the noble gases are placed in a separate group?
Answer:
Noble gases like helium (He), neon (Ne) and argon (Ar) are chemically very inert and are present in extremely low concentrations in our atmosphere. Hence they are placed in a separate s group.

Question 8.
How could the modern periodic table remove various anomalies of Mendeleev’s periodic table?
Answer:
The modern periodic table removed three main anomalies of Mendeleev’s periodic table as discussed below:
(1) Position of isotopes : All the isotopes of an element have the same atomic number. Therefore, they are placed at one place in the same group of the periodic table.

(2) Anomalous position of some pairs of elements: In the Mendeleev’s periodic table, elements with similar properties are placed in the same group. For example, cobalt (atomic mass 58.9 u) placed first and nickel (atomic mass 58.7 u) placed later while in the modern periodic table elements are arranged in increasing order of their atomic numbers, therefore, cobalt with atomic number 27 placed first and nickel with atomic number 28 placed later.

(3) Uncertainty in discovery of new elements: Since atomic masses do not increase in a regular manner in going from one element to the next, therefore, in Mendeleev’s periodic table, it was not possible to predict as to how many new elements could be discovered between two known elements.

Since, modern periodic table is formed on the basis of atomic numbers of elements, discovery of new element become easy.

Question 9.
Name two elements you would expect to show chemical reactions similar to magnesium. What is the basis for your choice?
Answer:
In the modern periodic table, elements having same number of electrons in the valence shell show similar chemical properties.
Magnesium has two electrons in the valence shell, hence all the elements such as beryllium (Be), calcium (Ca) and strontium (Sr) having two electrons in the valence shell show similar chemical properties.

Elements of group 2
Element	Atomic number	Electronic configuration
		K	L	M	N	O
Beryllium (Be)	4	2	2
Magnesium (Mg)	12	2	8	2
Calcium (Ca)	20	2	8	8	2
Strontium (Sr)	38	2	8	18	8	2

Question 10.
Name :
(a) three elements that have a single electron in their outermost shells.
(b) two elements that have two electrons in their outermost shells.
(c) three elements with filled outermost shells.
Answer:
(a) Lithium (Li), sodium (Na) and potassium (K)
(b) Magnesium (Mg) and calcium (Ca)
(c) Neon (Ne), argon (Ar) and krypton (Kr)

Question 11.
(a) Lithium, sodium, potassium are all metals that react with water to liberate hydrogen gas. Is there any similarity in the? atoms of these elements?
(b) Helium is an unreactive gas and neon is a gas of extremely low reactivity. What, if anything, do their atoms have in common?
Answer:
(a) Lithium, sodium and potassium are alkali metals which react with water to form metal hydroxides with the release of hydrogen gas.
2M + 2H₂O → 2MOH + H₂
Where, M = Li, Na and K
All these metals have one electron in their respective valence shells.

(b) Helium and neon are noble gases. Both the elements have their outermost shells completely filled. Helium has only K shell which is complete with 2 electrons while neon has two shells, K and L. Both these shells are complete, i.e., K s shell has 2 electrons and L shell has 8 electrons.

Question 12.
In the modern periodic table, which are the metals among the first ten elements?
Answer:
The first ten elements of the modern periodic table are as follows :
₁H, ₂He, ₃Li, ₄Be, ₅B, ₆C, ₇N, ₈O, ₉F and ₁₀Ne.
Among these elements Li and Be are metals.

Question 13.
By considering their position in the periodic table, which one of the following elements would you expect to have maximum metallic characteristics?
Ga Ge As Se Be
Answer:
Among the given elements, Be and Ga will show maximum metallic characteristics.
The arrangement of given elements in different groups and periods is as follows :

Activity 5.1 [T. B. Pg. 84]

Looking at its resemblance to alkali metals and the halogen family, try to assign hydrogen a : correct position in Mendeleev’s periodic table.
To which group and period should hydrogen be assigned ?

Discussion:

• Hydrogen is an element having lowest atomic number (Z = 1) and lowest atomic mass (1.008 u).
• The electronic configuration of hydrogen resembles with alkali metals.
• Like alkali metals, hydrogen combines with halogens, oxygen and sulphur to form compounds having similar molecular formulae. Hence, hydrogen can be placed along with alkali metals of group (IA).
• Hydrogen exists as a diatomic molecule like halogens and it combines with alkali metals to form ionic compounds and with non-metals to form covalent compounds.
• Thus, hydrogen should be placed along with halogens in group (VII).

Conclusion :
The position of hydrogen in the periodic table is controversial, however, it would be more appropriate to place it in group I and period I.

Activity 5.2 [T. B. Pg. 85]

• Consider the isotopes of chlorine, Cl-35 and Cl-37.
• There are two known isotopes of chlorine : Cl-35 and Cl-37.
• The atomic number of these two isotopes is 17, hence they have similar electronic configuration and chemical properties, but their atomic masses are different.

Questions :

Question 1.
Would you place them in different slots because their atomic masses are different?
Answer:
According to Mendeleev’s periodic table, “The properties of elements are the periodic function of their atomic masses.”

• According to Mendeleev, if these two isotopes are arranged in the order of increasing atomic masses, then their position should be before K(39.1u), but there is no vacant position available for Cl-37 in between Cl-35 and K(39.1u). Therefore they cannot be placed at the different position.

Question 2.
Would you place them in the same position because their chemical properties are the same?
Answer:
As they have similar chemical properties, they should be placed at the same position in group 17.

Activity 5.3 [T. B. Pg. 85]

Questions:

Question 1.
How were the positions of cobalt and nickel resolved in the modern periodic table?
Answer:

• In modern periodic table, elements are arranged in increasing order of their atomic numbers.
• The atomic number of cobalt and nickel are 27 and 28 respectively. Hence, on the basis of increasing order of their atomic numbers, cobalt is placed s in group 9 and nickel is placed in group 10.

Question 2.
How were the positions of isotopes of various elements decided in the modern periodic table?
Answer:
In the modern periodic table, positions of isotopes of different elements are not fixed separately. Since the various isotopes of an element have the same atomic number, they are assigned the same position in the modern periodic table.

Question 3.
Is it possible to have an element with atomic number 1.5 placed between hydrogen and helium?
Answer:

• The atomic number of an element is always definite and whole number.
• In the modern periodic table, elements are arranged in increasing order of their atomic numbers.
• The atomic number cannot be represented in fraction number. Thus, an element with atomic number 1.5 cannot be placed between hydrogen S and helium.

Question 4.
Where do you think should hydrogen be placed in the modern periodic table?
Answer:
Hydrogen should be placed in period and group 1 in the modern periodic table, $ since it has atomic number one.

Activity 5.4 [T. B. Pg. 87]

Questions:

Question 1.
Look at the group 1 of the modern periodic table and name the elements present in it.
Answer:
The names of the elements present in group 1 are: hydrogen (H), lithium (Li), sodium (Na), potassium (K), rubidium (Rb), cesium (Cs) and francium (Fr).

Question 2.
Write down the electronic configuration of the first three elements of group 1.
Answer:
The electronic configuration of the first three elements are as follows :

Element	H	Li	Na
Shell	K	K, L	K, L, M
Electronic configuration	1	2, 1	2, 8, 1

Question 3.
What similarity do you find in their electronic configurations?
Answer:
These elements possesses same number of electrons in their valence shell.

Question 4.
How many valence electrons are present in these three elements?
Answer:
These three elements have one electron in their respective valence shell.

Activity 5.5 [T. B. Pg. 87]

Questions:

Question 1.
If you look at the modern periodic table, you will find that the elements Li, Be, B, C, N, O, F and Ne are present in the second period. Write down their electronic configurations.
Answer:

Element	3Li	4Be	5B	6C	7NN	8O	9F	10Ne
Shell	K, L	K, L	K, L	K, L	K, L	K, L	K, L	K, L
Electronic configuration	2, 1	2, 2	2, 3	2, 4	2, 5	2, 6	2, 7	2, 8

Question 2.
Do these elements also contain the same number of valence electrons?
Answer:
These elements do not contain the same number of valence electrons.

Question 3.
Do they contain the same number of shells?
Answer:
These elements contain the same number of shells (2, K and L).

Activity 5.6 [T. B. Pg. 88]

Questions :

Question 1.
How do you calculate the valency of an element from its electronic configuration?
Answer:
The valency of an element is determined by the number of valence electrons present in the outermost shell of the atom.
For elements of group 1, 2, 13 and 14, the valency is equal to the number of valence electrons and for elements of group 15, 16, 17 and 18, the valency is equal to 8 minus number of valence electrons.

Question 2.
What is the valency of magnesium with atomic number 12 and sulphur with atomic number 16?
Answer:
Electronic configuration of Mg with atomic number 12 is K L M 2 8 2
∴ Valency of Mg = 2
Electronic configuration of S with atomic number 16 is K L M 2 8 6
∴ Valency of S = 8 – 6 = 2

Question 3.
Find the valency of the first twenty elements.
Answer:

Element	Atomic number	Group number	Electronic configuration				Number of valence electrons	Valency of the element
			K	L	M	N
H	1	1	1				1	1
He	2	18	2				2	2-2 = 0
Li	3	1	2	1			1	1
Be	4	2	2	2			2	2
B	5	13	2	3			3	3
C	6	14	2	4			4	4
N	7	15	2	5			5	8-5 = 3
O	8	16	2	6			6	8-6 = 2
F	9	17	2	7			7	8-7=1
Ne	10	18	2	8			8	8-8 = 0
Na	11	1	2	8	1		1	1
Mg	12	2	2	8	2		2	2
Al	13	13	2	8	3		3	3
Si	14	14	2	8	4		4	4
P	15	15	2	8	5		5	8-5 = 3
S	16	16	2	8	6		6	8-6 = 2
Cl	17	17	2	8	7		7	8-7=1
Ar	18	18	2	8	8		8	8-8 = 0
K	19	1	2	8	8	1	1	1
Ca	20	2	2	8	8	2	2	2

Question 4.
How does the valency vary in a period on going from left to right?
Answer:
In a period, the valency first increases and then decreases. In a period, the valency first increases from 1 to 4 and then decreases from 4 to 0.

Question 5.
How does the valency vary in going down a group?
Answer:
On moving down the group, the valency does not change. It remains constant.

Activity 5.7 [T. B. Pg. 88]

Questions:

Question 1.
Atomic radii of the elements of the second period are given below:

Period II elements:	B	Be	O	N	Li	C
Atomic radius (pm):	88	111	66	74	152	77

Arrange them in decreasing order of their atomic radii.
Answer:
Decreasing order of the atomic radii:
Period II elements : Li > Be > B > C > N > O
Atomic radius (pm) : 152  111 88 77 74 66

Question 2.
Are the elements now arranged in the pattern of a period in the periodic table?
Answer:
Now, the above elements are arranged in the pattern of a period in the periodic table.

Question 3.
Which elements have the largest and the smallest atoms?
Answer:
Lithium (Li) has the largest and oxygen (O) has the smallest atoms.

Question 4.
How does the atomic radius change as you go from left to right in a period?
Answer:
The atomic radii decreases as we move from left to right in a period.

Activity 5.8 [T. B. Pg. 89]

Questions:

Question 1.
Study the variation in the atomic radii of ? first group elements given below and arrange them in an increasing order.

Group I elements :	Na	Li	Rb	Cs	K
Atomic radius (pm):	186	152	244	262	231

Answer:
Increasing order of the atomic radii:
Group I elements : Li < Na < K < Rb < Cs
Atomic radius (pm): 152 186 231 244 262

Question 2.
Name the elements which have the smallest and the largest atoms.
Answer:
Lithium (Li) has the smallest atoms while Cesium (Cs) has the largest atoms.

Question 3.
How does the atomic size vary as you go down a group ?
Answer:
As we go down a group, the atomic size increases gradually.

Activity 5.9 [T. B. Pg. 89 ]

Questions:

Question 1.
Examine elements of the third period and classify them as metals and non-metals.
Answer:
The elements of the third period :

Question 2.
On which side of the periodic table do you find the metals?
Answer:
Metals are present on the left side of the periodic table.

Question 3.
On which side of the periodic table do you find the non-metals?
Answer:
Non-metals are present on the right side of the periodic table.

Activity 5.10 [T. B. Pg. 89]

Questions:

Question 1.
How do you think the tendency to lose electrons changes in a group?
Answer:
As we move from top to bottom in a group, the tendency to lose electrons increases.

Question 2.
How will this tendency change in a period?
Answer:
As we move from left to right in a period, the tendency to lose electrons decreases.

Activity 5.11 [T.B.Pg. 90]

Questions:

Question 1.
How would the tendency to gain electrons change as you go from left to right across a period?
Answer:
As we go from left to right across a period, the tendency to gain electrons increases.

Question 2.
How would the tendency to gain electrons change as you go down a group?
Answer:
As we go down a group, the tendency to gain electrons decreases.

Students should go through these JAC Class 10 Maths Notes Chapter 14 सांख्यिकी will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 14 सांख्यिकी

भूमिका :
पिछली कक्षाओं में आपने विभिन्न आलेखों जैसे कि दंड आलेख, आयत चित्र, बारम्बारता बहुभुज के माध्यम से दिए हुए आँकड़ों को अवर्गीकृत एवम् वर्गीकृत बारम्बारता बंटनों में व्यवस्थित करना सीखा था तथा अवर्गीकृत आँकड़ों की केन्द्रीय प्रवृत्ति की मापें जैसे कि माध्य, माध्यक, बहुलक के बारे में भी अध्ययन किया था। इस अध्याय में हम वर्गीकृत आँकड़ों के माध्य, माध्यक और बहुलक कैसे ज्ञात किया जाता है सीखेंगे और संचयी बारम्बारता, संचयी बारम्बारता वक्रों, जो तोरण कहलाती है, को किस प्रकार खींचा जाता है, सीखेंगे।
→ सांख्यिकी (Statistics) : सांख्यिकी वह विज्ञान है, जिसमें आँकड़ों का संग्रह तथा वर्गीकरण किया जाता है तथा उनका विश्लेषण करके उनकी व्याख्या की जाती है।
सांख्यिकी को लैटिन शब्द ‘स्टेट्स (Status) या जर्मन शब्द स्टे (Statistic ) या इटेलियन शब्द स्टेटिस्टा (Statista) से लिया गया है।
→ प्रेक्षण (Observation) : सांख्यिकीय आँकड़ों का प्रत्येक पद प्रेक्षण कहलाता है।
→ बारम्बारता (Frequency) : किसी सारणी में किसी पद की बारम्बारता कई बार हो, तो वह पद जितनी बार आता है उसे पद की बारम्बारता कहते हैं।
→ बारम्बारता सारणी (Frequency table) : वर्ग अन्तराल के अनुसार वर्गीकरण करके जो सारणी बनती है उसे बारम्बारता सारणी कहते हैं।
→ वर्ग की सीमाएँ (Class limits) : वर्ग को निश्चित करने के लिए दो संख्याएँ प्रयोग की जाती हैं, जो उस वर्ग की सीमाएँ कहलाती हैं।
पहली संख्या वर्ग की निम्न सीमा तथा दूसरी संख्या वर्ग की उच्च सीमा कहलाती है।
→ वर्ग अन्तराल (Class size) : किसी वर्ग की उच्च सीमा तथा निम्न सीमा का अन्तर वर्ग अन्तराल कहलाता है।
→ वर्ग चिह्न (Class marks) : एक वर्ग अन्तराल का मध्य बिन्दु या वर्ग चिह्न उसकी उच्च और निम्न सीमाओं का औसत मान होता है।

→ संचयी बारम्बारता (Cumulative Frequency) : किसी वर्ग की संचयी बारम्बारता उस वर्ग तथा उस वर्ग तक के सभी वर्गों की बारम्बारताओं के योग बराबर होती है।
(i) समान्तर माध्य (Arithmetic Mean) : “वह मान है जो दिये हुए आँकड़ों के योगफल को, आँकड़ों की संख्या से भाग देने पर प्राप्त होता है।”
(ii) बहुलक (Mode) : सांख्यिकीय आँकड़ों में जिस पद की बारम्बारता सबसे अधिक होती है, बहुलक कहलाता है अथवा दिए गए आँकड़ों (प्रेक्षणों) में सबसे अधिक बार आने वाले आँकड़ों को बहुलक कहते हैं।
(iii) माध्यक (Median) : केन्द्रीय प्रवृत्ति का ऐसा मापक जो आँकड़ों में सबसे बीच के प्रेक्षण का मान देता है माध्यक कहलाता है।
केन्द्रीय प्रवृत्ति-“आँकड़ों में से किसी एक आँकड़े के पास जाने की उनकी प्रवृत्ति को केन्द्रीय प्रवृत्ति कहते हैं।”

1. प्राप्त आँकड़ों से समान्तर माध्य ज्ञात करना :
इस प्रकार यदि किसी चर राशि के n मान क्रमश: x₁, x₂, ……, x_n हों तो उनका
समान्तर माध्य = \(\frac{x_1+x_2+\ldots \ldots+x_n}{n}\) या \(\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\) [सूत्र रूप] …..(i)
प्रतीक : (i) Σ (सिग्मा) ग्रीक वर्णमाला का एक अक्षर है और गणित में इसको योग या संकलन (Summation) की प्रक्रिया दर्शाने के लिए प्रयोग में लाया जाता है।
\(\sum_{i=1}^n x_i=x_1+x_2+\ldots \ldots \ldots+x_n\)
(ii) \(\bar{x}\) [x bar] द्वारा समान्तर माध्य प्रकट किया जाता है।
(iii) समान्तर माध्य को संक्षेप में माध्य भी कहते हैं।

2. यदि आँकड़े बारम्बारता सारणी के रूप में दिए हों तो माध्य का अवकलन निम्न प्रकार किया जाता है:
(i) प्रत्यक्ष विधि (Direct Method)
(ii) कल्पित माध्य विधि (Assumed Mean Method) या संक्षेप विधि (Shortcut Method)
(iii) पद-विचलन विधि (Step-deviation Method)
अवर्गीकृत बारम्बारता बंटन से समान्तर माध्य :
क्रिया पद (Working Steps) :
पद I : प्रत्येक विचर को उसकी बारम्बारता से गुणा (f_i × x_i) कीजिए।
पद II : ऐसे सभी गुणनफलों का योगफल ज्ञात कीजिए।
पद III : उपर्युक्त योगफल में बारम्बारता के योगफल का भाग दीजिए।
पद IV : इस प्रकार प्राप्त भागफल समान्तर माध्य होगा।
प्रत्यक्ष विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है:
माध्य = \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}\)

वर्गीकृत आँकड़ों का समान्तर माध्य :
क्रिया पद (Working Steps) :
पद I : वर्गीकृत बंटन में प्रत्येक वर्ग के मध्यमानों को ज्ञात कर उन्हें विचर x से प्रदर्शित कीजिए।

पद II : प्रत्येक वर्ग के मध्यमान को उसकी संगत बारम्बारता से गुणा कीजिए। (किसी वर्ग का मध्यमान उस वर्ग की निम्न एवं उच्च, दोनों सीमाओं के योगफल का आधा होता है।)
पद III : उपर्युक्त सभी गुणनफलों के योगफल में बारम्बारताओं के योगफल का भाग दीजिए।
पद IV : यह भागफल ही समान्तर माध्य होगा।
प्रत्यक्ष विधि में निम्नलिखित सूत्र का प्रयोग किया जाता है :
माध्य x \(\bar{x}=\frac{\sum f_i x_i}{\sum f_i}\)

कल्पित माध्य विधि (Assumed mean method) या संक्षेप विधि (Short-cut method) :
समान्तर माध्य (\(\bar{x}\)) = \(A+\frac{\sum f_i d_i}{\sum f_i}\)
जहाँ di = x_i – A, A = कल्पित माध्य
Σf_i = N = बारम्बारताओं का योग
नोट : सामान्यतः कल्पित माध्य विचर x का वह मान (अथवा मध्यमान) लिया जाता है जिसकी बारम्बारता अधिकतम हो। ऐसा करने से गणितीय परिकलन सरल हो जाता है।

पद-विचलन विधि (Step-deviation method) : इस विधि में विचलनों d_i = x_i – A के सभी मानों को किसी एक उभयनिष्ठ संख्या (माना h) से भाग देते हैं। ऐसी स्थिति में इन सभी विचलनों को h से विभाजित करते हुए नये विचलन \(u_i=\frac{x_i-A}{h}\) के रूप में लेते हैं।

जहाँ \(u_i=\frac{x_i-A}{h}\)
A = कल्पित माध्य
h = वर्ग माप
Σf_i = N = बारम्बारताओं का योगे

वर्गीकृत आँकड़ों का बहुलक :
आँकड़ों के किसी संग्रह या संकलन में जिस प्रेक्षण की बारम्बारता (आवृत्ति) अधिकतम होती है, उस प्रेक्षण के मान को बहुलक कहते हैं।
जैसे: (i) एक कक्षा के 20 छात्रों की आयु वर्षों में निम्न प्रकार हैं, इसका बहुलक ज्ञात करना है :
15 16 13 14 14 13 15 14 13 13
14 12 15 14 16 13 14 14 13 15
उक्त बंटन से स्पष्ट है कि आयु 14 वर्ष सबसे अधिक 7 बार आया है। इसकी बारम्बारता सबसे अधिक है। अतः बहुलक 14 होगा।
(ii) कुछ विद्यार्थियों के प्राप्तांक निम्न प्रकार हैं, इनका बहुलक ज्ञात करना है :

हल: यहाँ प्राप्तांक 34 की बारम्बारता सबसे अधिक 20 है।
अतः बहुलक = 34 अंक होगा।

वर्गीकृत बारम्बारता बंटन से बहुलक :
(Mode from Grouped Frequency Distribution)
वर्गीकृत बारम्बारता बंटन से बहुलक निकालने के लिए अग्र क्रिया पद हैं:
पद I. वर्गीकृत बारम्बारता बंटन के जिस वर्ग की बारम्बारता सबसे अधिक होती है, उसे बहुलक वर्ग (modal class) कहते हैं। सर्वप्रथम बहुलक वर्ग को ज्ञात करते हैं।
पद II. बहुलक वर्ग के माध्यम से निम्न सूत्र का प्रयोग करते हुए बहुलक ज्ञात करते हैं:
बहुलक = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
जहाँ l = बहुलक वर्ग की निम्न सीमा
f₁ = बहुलक वर्ग की बारम्बारता
f₀ = बहुलक वर्ग से ठीक पूर्व वर्ग की बारम्बारता
f₂ = बहुलक वर्ग के ठीक बाद के वर्ग की बारम्बारता
h = बहुलक वर्ग का अन्तराल

माध्यिका या माध्यक (Median) :
1. अवर्गीकृत या व्यक्तिगत श्रेणी से माध्यिका (Median from Ungrouped or Individual Series) : यदि किसी चर राशि x के मानों को आरोही (ascending) या अवरोही (descending) क्रम में रखा जाए, तो इस श्रेणी के मध्य (बीच) के पद को श्रेणी की माध्यिका या माध्यक (Median) कहते हैं।
(i) यदि पदों की संख्या विषम है, तो मध्य में एक ही पद \(\frac{n+1}{2}\) वाँ होगा।
माध्यक (M) = \(\frac{n+1}{2}\) वाँ होगा।
(ii) यदि पदों की संख्या सम है, तो

संचयी बारम्बारता बंटन का आलेखीय निरूपण (Graphical Representation of Cumulative Frequency) :
बारम्बारता बहुभुज तथा वक्र बनाने की दो विधियाँ हैं :
(1) ‘से कम’ विधि, (2) ‘से अधिक’ विधि।
(1) ‘से कम विधि’ (‘Less than’ method) : (i) वर्ग अन्तरालों की उच्च सीमा से प्रारम्भ करते हैं तथा वर्ग बारम्बारताओं को जोड़कर संचयी बारम्बारता (c.f.) बनाते हैं।
(ii) एक उचित पैमाना लेकर वर्गों की उच्च सीमा को X-अक्ष के अनुदिश निरूपित करते हैं।
(iii) एक उचित पैमाना लेकर संचयी बारम्बारताओं को Y-अक्ष के अनुदिश निरूपित करते हैं।
(iv) ग्राफ पर बिन्दुओं (x_i, f_i) को अंकित करते हैं, जहाँ x_i किसी वर्ग की उच्च सीमा तथा f_i संगत संचयी बारम्बारता है।
(v) चरण (iv) से प्राप्त बिन्दुओं को हाथ से वक्र के रूप में जोड़कर संचयी बारम्बारता वक्र अथवा तोरण प्राप्त करते है।

(2) से अधिक’ विधि (‘More than’ method) :
(i) वर्ग अन्तरालों की निम्न सीमा से प्रारम्भ करते हैं तथा बारम्बारताओं के योग में से प्रत्येक वर्ग की बारम्बारता घटाकर संचयी बारम्बारता बंटन प्राप्त करते हैं।
(ii) एक उचित पैमाना लेकर वर्गों की निम्न सीमा को X-अक्ष के अनुदिश निरूपित करते हैं।
(iii) एक उचित पैमाना लेकर संचयी बारम्बारताओं को Y-अक्ष के अनुदिश निरूपित करते हैं।
(iv) ग्राफ पर बिन्दुओं (x_i, f_i) को अंकित करते हैं, जहाँ x_i किसी वर्ग की निम्न सीमा तथा fi संगत संचयी बारम्बारता हैं।
(v) चरण (iv) से प्राप्त बिन्दुओं को हाथ से वक्र से रूप में जोड़कर बारम्बारता वक्र अथवा तोरण प्राप्त करते हैं।

तोरण अथवा वक्र द्वारा माध्यक ज्ञात करने की विधि : (i) ग्राफ पेपर पर दो प्रकार के बारम्बारता वक्रों में से एक खींचते हैं।
(ii) \(\frac{N}{2}\)(N = Σf_i) ज्ञात कर, Y-अक्ष पर संगत बिन्दु अंकित करते हैं।
(iii) इस संगत बिन्दु से X-अक्ष के समान्तर रेखा खींचते हैं जो वक्र को एक बिन्दु (माना P) पर काटती है।
(iv) यह बिन्दु P का भुज अर्थात् बिन्दु P का x-निर्देशांक माध्यिका होगी।

Students should go through these JAC Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

भूमिका (Introduction) :
पिछली कक्षाओं में हम ठोस आकृतियों जैसे घनाभ, घन, शंकु, बेलन और गोला के पृष्ठीय क्षेत्रफल तथा आयतन के बारे में अध्ययन कर चुके है। इस अध्याय में पिछले ज्ञान का उपयोग करते हुए दो या दो से अधिक ठोस आकृतियों के संयोजन से बनी आकृतियों के पृष्ठीय क्षेत्रफल तथा आयतन का अध्ययन करेंगे। हम ऐसी ठोस आकृतियों के बारे में भी अध्ययन करेंगे जो एक शंकु को उसके आधार के समान्तर एक तल द्वारा काटने पर प्राप्त होते है। उदाहरण के लिए बाल्टी, ग्लास, फ्रिक्शन क्लच आदि।
→ ठोस (Solid) : वस्तुएँ जिनकी अन्तरिक्ष में तीन भुजाएँ अर्थात् (लम्बाई, चौड़ाई, ऊँचाई) हों ठोस कहलाते हैं।
→ आयतन (Volume) : किसी ठोस द्वारा अन्तरिक्ष के घेरे गए स्थान के परिमाण को उसका आयतन कहते हैं।
→ पृष्ठीय क्षेत्रफल (Surface area) : किसी ठोस के सभी पृष्ठों के क्षेत्रफलों के योग को उसका पृष्ठीय क्षेत्रफल कहते हैं।
→ वक्त पृष्ठीय क्षेत्रफल (Lateral surface area) : किसी ठोस के आधार क्षेत्रफलों को छोड़कर शेष बचे सभी पृष्ठों के क्षेत्रफलों के योग को वक्र पृष्ठीय क्षेत्रफल कहते हैं।
→ घनाभ (Cuboid): छ: आयताकार पृष्ठों से घिरी ठोस बन्द आकृति को घनाभ कहते हैं।
→ घन (Cube) : यदि घनाभ की प्रत्येक कोर लम्बाई में समान हो, तो उसे घन कहते हैं।
→ लम्ब वृत्तीय शंकु का छिन्नक (Frustum of a right circular cone) : यदि किसी लम्ब वृत्तीय शंकु को उसके आधार के समान्तर किसी तल द्वारा काटा जाये तो कटने वाले तल तथा आधार के बीच के भाग को शंकु का छिन्नक कहते हैं।

घन (Cube) और घनाभ (Cuboid) :
घनाभ (Cuboid) : यदि समान्तर षट्फलक का प्रत्येक फलक आयत हो, तो उसे घनाभ कहते हैं। घनाभ को आयतफलकी ठोस भी कहते हैं जैसे ईंट, सन्दूक, कमरा आदि घनाभ हैं घनाभ में छः पृष्ठ (फलक), 8 शीर्ष व 12 कोरें होती हैं।
चित्र से स्पष्ट है कि घनाभ के आमने-सामने के फलक परस्पर समान होते हैं।

1. घनाभ के फलक ABCD का क्षेत्रफल = फलक A’B’CD’ का क्षेत्रफल = लम्बाई × चौड़ाई
2. घनाभ के फलक ADD’A’ का क्षेत्रफल = फलक BCC’B’ का क्षेत्रफल = चौड़ाई × ऊँचाई
3. घनाभ के फलक ABB’A’ का क्षेत्रफल = फलक DCC’D’ का क्षेत्रफल = ऊँचाई × ऊँचाई
4. घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई) वर्ग इकाई
5. घनाभ की चारों दीवारों का क्षेत्रफल = 2 × ऊँचाई (लम्बाई + चौड़ाई) वर्ग इकाई
अथवा
= (ऊँचाई × परिमाप) वर्ग इकाई।

घन (Cube) : यदि घनाभ का प्रत्येक फलक वर्गाकार हो, तो उसे घन कहते हैं। अर्थात् घन की लम्बाई, चौड़ाई और ऊँचाई बराबर होती हैं।
∴ घन का प्रत्येक पृष्ठ वर्गाकार होता है।
घन के एक पृष्ठ का क्षेत्रफल = (भुजा)²
∴ घन के 6 पृष्ठों का क्षेत्रफल = 6(भुजा)²
अतः घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6(भुजा)² वर्ग इकाई

घन और घनाभ के विकर्ण (Diagonals of Cube and Cuboid)
घन या घनाभ के समान्तर फलक के दो सम्मुख शीर्षों को मिलाने वाली रेखा विकर्ण कहलाती है अतः घन एवं मैं कुल 4 विकर्ण होते हैं।
1. घनाभ के विकर्ण की लम्बाई =
2. घन के विकर्ण की लम्बाई = भुजा \(\sqrt{3}\) इकाई
घन और घनाभ का आयतन (Volume of Cube and Cuboid)
प्रत्येक ठोस आकृति स्थान घेरती है। अतः ठोस आकृति द्वारा घेरे गये स्थान की माप को आयतन कहा जाता है।
घनाभ का आयतन = (लम्बाई × चौड़ाई × ऊँचाई ) घन इकाई तथा घन का आयतन = (भुजा)³ घन इकाई।

लम्बवृत्तीय बेलन और शंकु :
लम्बवृत्तीय बेलन (Right Circular Cylinder) :
परिभाषा- किसी ‘आयत’ की एक भुजा को स्थिर रखकर उसके परित: आयत को घुमाने पर बने ठोस को लम्बवृत्तीय बेलन कहते हैं।
संलग्न चित्र में आयत OABC की भुजा OA को स्थिर मानकर उसके परितः आयत को घुमाने पर बने लभ्यवृत्तीय बेलन को दिखाया गया है।
स्थिर भुजा OA की लम्बाई को बेलन की ऊँचाई कहते हैं तथा बिन्दु O और A इसके वृत्तीय सिरों के केन्द्र कहलाते हैं। OC अथवा AB इसके वृत्तीय आधार की त्रिज्या हैं। आयत को उसकी किसी एक भुजा के परितः घुमाने पर लम्बवृत्तीय बेलन प्राप्त होता है।

लम्बवृत्तीय बेलन से सम्बन्धित सूत्र
1. बेलन के आधार का क्षेत्रफल = वृत्त का क्षेत्रफल = πr² वर्ग इकाई
2. बेलन के आधार की लम्बाई = वृत्त की परिधि = 2πr इकाई
3. बेलन के वक्रपृष्ठ का क्षेत्रफल (C.S.A.) = आधार की परिधि × ऊँचाई
= 2πrh वर्ग इकाई
4. बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) = वक्रपृष्ठ का क्षेत्रफल + दोनों वृत्तीय आधारों का क्षेत्रफल
= 2πrh + 2πr² = 2πr (h + r) वर्ग इकाई
5. बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई = πr² × h = πr2h घन इकाई

खोखला बेलन (Hollow Cylinder)- यदि r₁ व r₂ खोखले बेलन की बाह्य और अन्तः त्रिज्याएँ हों तथा ऊँचाई h हो तो :
1. खोखले बेलन के प्रत्येक सिरे का क्षेत्रफल = π(r₁² – r₂²)
2. खोखले बेलन के वक्रपृष्ठ का क्षेत्रफल = बाह्य पृष्ठ का क्षेत्रफल + अन्तः पृष्ठ का क्षेत्रफल
= 2πr₁h + 2πr₂h = 2π(r₁ + r₂)h
3. खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्रपृष्ठ का क्षेत्रफल + 2 × (एक सिरे का क्षेत्रफल)
= 2π(r₁ + r₂)h + 2π(r₁² – r₂²)
= 2π(r₁ + r₂)h + 2π(r₁ + r2) (r₁ – r₂)
= 2π(r₁ + r₂) (h + r₁ – r₂)
4. खोखले बेलन का आयतन = बाह्य बेलन का आयतन – अन्तः बेलन का आयतन
= πr₁²h – πr₂²h = π(r₁² – r₂²)h

लम्बवृत्तीय शंकु (Right Circular Cone) :
परिभाषा- किसी समकोण त्रिभुज की समकोण बनाने वाली दो भुजाओं में से एक को स्थिर मानकर, त्रिभुज को उसके परितः घुमाने पर बने ठोस को लम्बवृत्तीय शंकु कहते हैं।
चित्र में समकोण ΔVOA को भुजा OV के परित: घुमाने पर प्राप्त लम्बवृत्तीय शंकु को दिखाया गया है, जिसका शीर्ष V तथा वृत्तीय आधार का केन्द्र O है।

यहाँ शंकु की ऊँचाई = OV = h
शंकु की तिरछी ऊँचाई = VA = l
शंकु के आधार की त्रिज्या = ∠OAP = α
शंकु का अर्द्ध-शीर्ष कोण
समकोण ΔVOA में, VA² = OV² + OA²
l² = h² + h²
l = \(\sqrt{h^2+r^2}\)
शंकु की तिरछी ऊँचाई (l) = \(\sqrt{h^2+r^2}\)

लम्बवृत्तीय शंकु से सम्बन्धित सूत्र :
1. शंकु का वक्रपृष्ठीय क्षेत्रफल (C.S.A.) = \(\frac{1}{2}\) × वृत्तीय आधार की परिधि × तिरछी ऊँचाई
= \(\frac{1}{2}\) × 2πr × l = πrl
2. शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) = वक्र पृष्ठ + वृत्तीय आधार का क्षेत्रफल
= πrl + πr² = πr(l + r)
3. शंकु का आयतन = \(\frac{1}{3}\) × वृत्तीय आधार का क्षेत्रफल × ऊँचाई = \(\frac{1}{3}\)πr²h
यदि शंकु का अर्द्ध-शीर्ष कोण α हो तो उसकी :
(i) ऊँचाई (h) = r cot α
(ii) तिर्यक ऊँचाई (l) = r cosec α

गोला (Sphere) :
जब किसी वृत्त या अर्द्धवृत्त को उसके व्यास के सापेक्ष परिक्रमण कराया जाता है, तो एक ठोस आकृति प्राप्त होती है जिसे गोला कहते हैं। वृत्त का केन्द्र, त्रिज्या और व्यास गोले के केन्द्र, त्रिज्या और व्यास होंगे।

यदि गोले की त्रिज्या r हो, तो
1. गोले का पृष्ठीय क्षेत्रफल = 4πr²
2. गोले का आयतन = \(\frac{4}{3}\)πr³

यदि अर्द्ध गोले की त्रिज्या r हो, तो
1. अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल = 2πr²
2. अर्द्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2πr² + πr² = 3πr²
3. अर्द्ध गोले का आयतन = \(\frac{2}{3}\)πr³

गोलीय कोश (खोखला गोला) (Spherical shell)- दो संकेन्द्रीय गोलों से सीमाबद्ध आकृति को गोलीय कोश कहते हैं।
यदि गोलीय कोश की बाह्य त्रिज्या r₁ और अन्तः त्रिज्या r₂ हो, तो
1. गोलीय कोश का आयतन = \(\frac{4}{3}\)π(r₁³ – r₂³)
2. गोलीय कोश की मोटाई = r₁ – r₂.

ठोसों के संयोजन का पृष्ठीय क्षेत्रफल :
निम्नांकित चित्रों में बनी आकृतियों पर ध्यान दीजिए:

चित्र (1) में दो घनों को संयुक्त करके एक आयतफलकी बनाया गया है।
चित्र (2) में दी गई आकृति एक बेलन के दोनों सिरों पर समान परिच्छेद क्षेत्रफल के दो शंकु जोड़कर बनाई गई है।
चित्र (3) में दी गई आकृति एक बेलन के दोनों सिरों पर समान परिच्छेद क्षेत्रफल के दो अर्द्धगोलों को संयुक्त कर बनाई गई है।
चित्र (4) में दी गई आकृति समान आधार वाले अर्द्धगोले पर शंकु के संयोजन से बनाई गई है।
नोट : (1) किसी संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल (T.S.A.) उसके खण्डों के सम्पूर्ण पृष्ठीय क्षेत्रफलों के योग से कम होता है और क्षेत्रफल में यह कमी उस क्षेत्रफल के बराबर होती है जो खण्डित भागों को संयुक्त करने पर विलुप्त हो जाता है।
(2) यदि संयुक्त ठोस के सभी खण्ड वक्र संयुक्त पृष्ठीय हैं, तो
संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = संयुक्त ठोस के खण्डों के वक्र पृष्ठों के क्षेत्रफल का योग
तथा संयुक्त ठोस का आयतन = संयुक्त ठोस के खण्डों के आयतनों का योग।

ठोसों के संयोजन का आयतन :
दो ठोसों के संयोजन से बने ठोस आकृति का आयतन वास्तव में दोनों के आयतनों के योग के बराबर होता है।
आयतन से सम्बन्धित सूत्र :
1. घनाभ का आयतन = ल. × चौ. × ॐ.
2. घन का आयतन = भुजा³
3. बेलन का आयतन = πr²h
4. शंकु का आयतन = \(\frac{1}{3}\)πr²h
5. खोखले बेलन का आयतन = π(r₁² – r₂²)h, जहाँ r₁ > r₂
6. गोले का आयतन = \(\frac{4}{3}\)πr³
7. अर्द्धगोले का आयतन = \(\frac{2}{3}\)πr³
8. खोखले गोले (गोलीय कोश) का आयतन = \(\frac{4}{3}\)π(r₁³ – r₂³), जहाँ r₁ > r₂

आयतन सम्बन्धी इकाइयाँ
1 लीटर = 1000 घन सेमी
1000 लीटर = 1 घन मीटर
1 किलो लीटर = 1 घन मीटर
1 घन सेमी = 10 × 10 × 10 = 1000 घन मिमी
1 घन मीटर = 100 × 100 × 100
= 1000000 घन सेमी

एक ठोस का एक आकार से दूसरे आकार में रूपान्तरण :
इस खण्ड में हम एक ठोस को एक रूप से दूसरे रूप में परिवर्तित करते हैं, तो इस पूरी स्थिति में दोनों आकारों का आयतन समान रहता है।
जैसे-जूस की एक बोतल को कुछ गिलासों में समान मात्रा में बाँट दें। अब हम गिलासों की संख्या ज्ञात करना चाहेंगे।
[जूस की बोतल का आयतन] = n[गिलासों का आयतन],
जहाँ गिलासों की संख्या है।

लम्बवृत्तीय शंकु का छिन्नक (Frustum of a Right Circular Cone) :
छिन्नक : यदि किसी लम्बवृत्तीय शंकु को उसके आधार के समान्तर तल द्वारा काटा जाता है, तो वह भाग जो शंकु के आधार तथा काटने वाले तल के बीच है, छिन्नक कहलाता है।

चित्र (i) में लम्बवृत्तीय शंकु VAB को उसके वृत्तीय आधार के समान्तर एक तल द्वारा काटा जाता है जिसका केन्द्र O तथा व्यास AB है। शीर्ष / वाले भाग को हटा दिया जाता है, जैसा कि चित्र (ii) में दिखाया गया है। शेष हुआ भाग ABB ‘A’ चित्र (iii) में दिखाया गया है, यह शंकु VAB का छिन्नक है वृत्तीय पृष्ठ AOB तथा A’O’B’ छिन्नक के वृत्तीय सिरे कहलाते हैं।
अतः लम्बवृत्तीय शंकु के छिन्नक के दो असमान वृत्तीय आधार होते हैं और एक वक्र पृष्ठ होता है।
छिन्नक की ऊँचाई: छिन्नक की ऊँचाई या मोटाई दोनों वृत्तीय आधारों के बीच की लम्बीय दूरी होती है।
छिन्नक की ऊँचाई OO’ = VO – VO’ (चित्र iii)
छिन्नक की तिर्यक ऊंचाई : छिन्नक के दोनों वृत्तीय आधारों पर एक ही दिशा में खींची समान्तर त्रिज्याओं के बाहरी बिन्दुओं को मिलाने वाले रेखाखण्ड की लम्बाई को छिन्नक की तिर्यक ऊँचाई कहते हैं।
चित्र में, छिन्नक ABA’B’ की तिर्यक ऊँचाई AA’ या BB’ हैं।
स्पष्ट है कि AA’ = VA – VA’
तथा BB’ = VB – VB’
अतः छिन्नक की तिर्यक ऊँचाई शंकुओं VAB और VA’B’ की तिर्यक ऊँचाइयों के अन्तर के बराबर होती है।

लम्बवृत्तीय शंकु के छिन्नक का आयतन और पृष्ठीय क्षेत्रफल :
शंकु के छिन्नक का आयतन = \(\frac{1}{3}\)π(r₁² – r₁ r₂ + r₂²)h
शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π(r₁ + r₂)l

शंकु के छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + वृत्तीय आधारों का पृष्ठीय क्षेत्रफल
= π(r₁ + r₂)l + πr₁² + πr₁²
= π[(r₁ + r₂)l + r₁² + r₂²]
शंकु के छिन्नक की (तिर्यक) ऊँचाई = \(\sqrt{\left(r_1-r_2\right)^2+h^2}\)

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 2 बहुपद

लयूत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
बहुपद ax² + bx + c के आलेखों की आकृतियाँ, चित्र में दी गयी हैं। प्रत्येक आकृति में a, b और c के चिह्न ज्ञात कीजिए:

हल :
(i) बहुपद y = ax² + bx + c का परवलय नीचे की ओर खुलता है।
∴ a < 0 होगा तथा परवलय का शीर्ष प्रथम चतुर्थांश में है। –\(\frac{b}{2a}\) > 0 ⇒ – b < 0 ⇒ b > 0
परलवय y-अक्ष को बिन्दु P पर प्रतिच्छेद करता है। y-अक्ष पर x = 0 होता हैं। x = 0 का मान समीकरण y = ax² + bx + c में रखने पर हम y = c प्राप्त करते हैं। अतः P के निर्देशांक (o, c) हैं। ∵ P, y- अक्ष की धनात्मक दिशा में है । अतः
∴ c > 0.
∴ a < 0, b > 0 तथा c > 0

(ii) दिशा है : y = ax² + bx + c परवलय ऊपर की ओर खुलता है। अत: a > 0 हैं। परवलय के शीर्ष चौथे चतुर्थाश में हैं।
∴ – \(\frac{b}{2a}\) > 0 ⇒ b < 0 ⇒ b < 0
परवलय y-अक्ष को बिन्दु p पर प्रतिच्छेद करता है। x = 0, अत: y = ax 2 + bx + c में x = 0 रखने पर y = c प्राप्त होता हैं।
∴ p के निर्देशांक (0, c) हैं।
∵ बिन्दु P, OY’ पर स्थित है। अतः c < 0 होगा। a > 0, b < 0 ओर c <0

(iii) बहुपद y = ax² + bx + c का परवलय ऊपर की ओर खुलता है। अतः a > 0 है।
परवलय का शीर्ष OX पर स्थित है।
∴ – \(\frac{b}{2a}\) > 0 ⇒ – b > 0 ⇒ b < 0 परवलय y = ax² + bx + c Y-अक्ष को बिन्दु P पर प्रतिच्छेद करता है जो OY पर स्थित है। समीकरण y = ax² + bx + c में x = 0 रखने पर, y = c प्राप्त होता है। अत: बिन्दु P के निर्देशांक (0, c) हैं। ∵ P, OY अक्ष पर स्थित है। ∴ c > 0 होगा।
∴ a > 0, b < 0 और c > 0.

(iv) परवलय y = ax² + bx + c नीचे की ओर खुलता है। अत: a < 0 है।
परवलय का शीर्ष (\(\frac{-b}{2a}\), \(\frac{-D}{4a}\))OX’ पर स्थित है।
∴ – \(\frac{b}{2a}\) < 0 ⇒ b > 0
परवलय y = ax² + bx + c, Y-अक्ष को P(0, c) पर प्रतिच्छेद करता है जो OY’ पर है। अतः c < 0 होगा।
∴ a < 0, b > 0 तथा c < 0.

प्रश्न 2.
यदि बहुपद p(x) = 2x² + 5x + k के शून्यक α तथा β, सम्बन्ध α² + β² + αβ = \(\frac{21}{4}\) को सन्तुष्ट करते हैं, तो k का मान ज्ञात कीजिए।
हल :
∵ αβ बहुपद p(x) = 2x² + 5x + k के शून्यक हैं।
∴ α + β = \(\frac{-5}{2}\)
तथा α × β = \(\frac{k}{2}\) ………(1)
α² + β² + αβ = \(\frac{21}{4}\) (दिया है)
⇒ α² + β² + 2αβ – αβ = \(\frac{21}{4}\) (αβ जोड़ने तथा घटाने पर)
⇒ (α + β)² – αβ = \(\frac{21}{4}\)
⇒ (\(\frac{-5}{2}\))² – \(\frac{k}{2}\) = \(\frac{21}{4}\)
[समी. (1) का प्रयोग करने पर]
⇒ \(\frac{25}{4}-\frac{k}{2}\) = \(\frac{21}{4}\)
\(\frac{25}{4}-\frac{21}{4}\) = \(\frac{k}{2}\)
\(\frac{4}{4}\) = \(\frac{k}{2}\)
\(\frac{k}{2}\) = 1
⇒ k = 2
अतः k = 2

प्रश्न 3.
यदि α और β द्विघात बहुपद f(x) = x² – px + g के शून्यक हैं तो निम्न के मान ज्ञात कीजिए :
(i) α² + β²
(ii) \(\frac{1}{α}=\frac{1}{β}\)
हल :
∵ α और β बहुपद f(x) = x² – px + q के शून्यक हैं।
∴ शून्यकों का योग (α + β) = – (\(\frac{-p}{1}\)) = p
शून्यकों का गुणनफल (αβ) = \(\frac{q}{1}\) = q

(i) α² + β² = (α + β)² – 2αβ
= p² – 2q

(ii) \(\frac{1}{α}=\frac{1}{β}\) = \(\frac{\alpha+\beta}{\alpha \beta}\) = \(\frac{p}{q}\)

प्रश्न 4.
यदि α, β द्विघात बहुपद f(x)= 2x² – 5x + 7 के शून्यक हों तो एक बहुपद ज्ञात कीजिए जिसके शून्यक 2α + 3β और 3α + 2β हों।
हल
∵ α और β द्विघात बहुपद f(x) = 2x² – 5x + 7 के शून्यक हैं।
∴ α + β = -(\(\frac{-5}{2}\)) = \(\frac{5}{2}\) और αβ = \(\frac{7}{2}\)
माना अभीष्ट बहुपद के शून्यकों के योग व गुणनफल को S व P से व्यक्त करें तो :
S = (2α + 3β) + (3α + 2β)
= 5(α + β) = 5 × \(\frac{5}{2}=\frac{25}{2}\)
या P = (2α + 3β) × (3α + 2β)
या P = 6(α² + β²) + 13αβ
या P = 6α² + 6β² + 12αβ + αβ
या P = 6 (α + β)² + αβ
या P = 6(\(\frac{5}{2}\))² + \(\frac{7}{2}\)
या P = 6 × \(\frac{25}{4}+\frac{7}{2}=\frac{75}{2}+\frac{7}{2}\)
∴ P = \(\frac{75+7}{2}=\frac{82}{2}\) = 41
अत: अभीष्ट बहुपद g(x) निम्न होगा :
g(x) = k(x² – Sx + P)
⇒ g (x) = k(x² – \(\frac{25}{2}\)x + 41)
जहाँ k एक अशून्य वास्तविक संख्या है।

प्रश्न 5.
बहुपद f(x) = 3x³ + ax² + 4x + b का एक गुणनखण्ड (x + 2) है। यदि इसमें (x – 3) का भाग दिया जाये तो शेषफल – 5 बचता है। a तथा b के मान ज्ञात कीजिए।
हल :
यहाँ f(x) = 3x³ + ax² + 4x + b का एक गुणनखण्ड (x + 2) है।
अत: x + 2 = 0
⇒ x = – 2 रखने पर
f(-2) = 0 होगा।
यहाँ f(x) = 3x³ + ax² + 4x + b
∴ f(-2) = 3(-2)³ + a(-2)² + 4(-2) + b
⇒ 0 = 3(-8) + a(4) – 8 + b
⇒ 0 = – 24 + 4a – 8 + b
⇒ 0 = 4a + b – 32
⇒ 4a + b = 32 ……..(i)
पुन: (x – 3) से भाग देने पर शेषफल – 5 बचता है।
अत: f(3) = – 5.
∵ f(x) = 3x³ + ax² + 4x + b
∴ f(3) = 3(3)³ + a(3)² + 4(3) + b
⇒ – 5 = 3 × 27 + a(9) + 12 + b
⇒ – 5 = 81 + 9a + 12 + b
⇒ – 5 = 93 + 9a + b
⇒ 9a + b = – 5 – 93
⇒ 9a + b = – 98 ….(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर,

∴ a = \(\frac{-130}{5}\) = – 26
a का मान समीकरण (i) में रखने पर,
⇒ 4(-26) + b = 32
⇒ – 104 + b = 32
∴ b = 32 + 104 = 136
अतः a = – 26 और b = 136 होगा।

प्रश्न 6.
3x³ + x² + 2x + 5 को 1 + 2x + x² से भाग दीजिए।
हल :
3x³ + x² + 2x + 5 ÷ 1 + 2x + x²
1 + 2x + x² को x² + 2x + 1 लिख सकते है

जाँच-
(3x – 5) (1 + 2x + x²) + 9x + 10
= 3x + 6x² + 3x² – 5 – 10x – 5x² + 9x + 10
= 3x³ + x² – 7x – 5 + 9x + 10
= 3x³ + x² + 2x + 5

प्रश्न 7.
x³ – 3x² + 3x – 5 को x – 1 – x² से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए।
हल :
माना कि
f(x) = x³ – 3x² + 3x – 5
तथा g(x) = x – 1 – x² = – x² + x + 1
अब f(x) को g(x) से विभाजित करेंगे।

अत: भागफल q(x) = – x + 2
तथा शेषफल (x) = – 3
विभाजन एल्गोरिथ्म के प्रयोग से भाग्य = भाजक × भागफल + शेषफल
⇒ x³ – 3x² + 3x – 5 = (- x² + x – 1) (- x + 2) – 3
⇒ x³ – 3x² + 3x – 5 = (x³ – 2x² – x² + 2x + x – 2) – 3
⇒ x³ – 3x² + 3x – 5 = x³ – 3x² + 3x – 2 – 3
⇒ x³ – 3x² + 3x – 5 = x³ – 3x² + 3x – 5
चूँकि बायाँ पक्ष = दायाँ पक्ष
अतः विभाजन एल्गोरिथ्म सत्यापित होता है।

प्रश्न 8.
वह प्रतिबन्ध ज्ञात कीजिए कि बहुपद p(x) = ax² + bx + c के शून्यक एक दूसरे के व्युत्क्रम हैं।
हल :
माना कि α बहुपद p(x) = ax² + bx + c का प्रथम शून्यक है।
प्रश्नानुसार बहुपद p(x) का दूसरा शून्यक (β) = \(\frac{1}{α}\)
α × β = \(\frac{c}{a}\)
⇒ α × \(\frac{1}{α}\) = \(\frac{c}{a}\)
⇒ 1 = \(\frac{c}{a}\)
⇒ c = a
अतः प्रतिबन्ध c = a है ।

प्रश्न 9.
x³ – 6x² + 11x – 6 को x – 2 से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए ।
हल :

अतः भागफल = x² – 4x + 3 तथा शेषफल = 0
विभाजन एल्गोरिथ्य की सत्यता
भागफल भाजक + शेषफल
= (x² – 4x + 3) × (x – 2) + 0
= x³ – 4x² + 3x – 2x² + 8x – 6
= x³ – 6x² + 11x – 6
= भाज्य
अतः भागफल × भाजक + शेपफल = भाज्य
इति सिद्धम्

प्रश्न 10.
यदि त्रिघातीय बहुपद x³ – 3x² – 10x + 24 का एक शून्यक 4 है, तो इसके अन्य दो शून्यक ज्ञात कीजिए।
हल :
माना p(x) = x³ – 3x² – 10x + 24
दिया है, 4, p(x) का एक शून्यक है।
∴ (x – 4), p(x) का एक गुणनखंड होगा।

भागफल = x² + x – 6 तथा शेषफल = 0
∴ x³ – 3x² – 10x + 24 = (x – 4)(x² + x – 6).
अब p(x) के अन्य शून्यक ज्ञात करने के लिए भागफल (x² + x – 6) = 0 रखकर गुणनखंड करने पर,
x² + x – 6 = 0
⇒ x² + 3x – 2x – 6 = 0
⇒ x(x + 3) – 2(x + 3) = 0
⇒ (x + 3) (x – 2) = 0
यदि x + 3 = 0, तो x = – 3
और यदि x – 2 = 0, तो x = 2
अत: – 3 और 2 बहुपद x³ – 3x² – 10x + 24 के अन्य दो गुणनखंड है।

प्रश्न 11.
एक अध्यापक ने अपने 10 विद्यार्थियों में से प्रत्येक को एक कागज पर एक चर वाला एक बहुपद लिखकर देने को कहा। विद्यार्थियों के उत्तर निम्न थे :
2x + 3, 3x² + 7x + 2, 4x² + 3x² + 2,
x² + \(\sqrt{3}\)x + 7, 5x³ – 7x + 2,
2x² + 3 – \(\frac{5}{x}\), 5x – \(\frac{1}{2}\),
ax³ + bx³ + cx + d, x + \(\frac{1}{x}\), x³ – 3
निम्न प्रश्नों के उत्तर दीजिए:
(i) उपरोक्त दस में कितने बहुपद नहीं हैं?
(ii) उपरोक्त दस में कितने द्विघात बहुपद हैं?
हल :
(i) तीन, x² + \(\sqrt{3x}\) + 7, 2x² + 3 – \(\frac{5}{x}\), x + \(\frac{1}{x}\) बहुपद नहीं है।
(ii) एक 3x² + 7x + 2 एक द्विघातीय बहुपद है।

प्रश्न 12.
यदि बहुपद f(x) = x² – 8x + k के शून्यकों के वर्गों का योग 40 है, तो का मान ज्ञात कीजिए।
हल :
दिया है, f(x) = x² – 8x + k
माना f(x) के शून्यक α और β हैं।
∴ शून्यकों का योग = – \(\frac{b}{a}\)
α + β = \(\frac{-(-8)}{1}\)
और शून्यकों का गुणन = \(\frac{c}{a}\)
αβ = \(\frac{k}{1}\)
प्रश्नानुसार, α² + β² = 40
हम जानते हैं कि
(α + β)² = α² + β² + 2αβ
⇒ (8)² = 40 + 2k
⇒ 64 – 40 = 2k
⇒ 24 = 2k
⇒ k = \(\frac{24}{2}\) = 12

प्रश्न 13.
बहुपद p(x) = 2x⁴ – x³ – 11x² + 5x + 5 के दो शून्यक \(\sqrt{5}\) और – \(\sqrt{5}\) है। इस बहुपद के अन्य दो शून्यक ज्ञात कीजिए।
हल :
\(\sqrt{5}\) और – \(\sqrt{5}\) दिए गए बहुपद के शून्यक है।
∴ (x – \(\sqrt{5}\))(x + \(\sqrt{5}\)) = x² – 5, दिए गए बहुपद का एक गुणनखंड होगा।

विभाजन एल्गोरिथ्य प्रमेय से
2x⁴ – x³ – 11x² + 5x + 5 = (2x² – x – 1)(x² – 5)
अब p(x) के अन्य दो शून्यक ज्ञात करने के लिए भागफल (2x² – x – 1) = 0 रखकर गुणनखंड करने पर
2x² – x – 1 = 0
⇒ 2x² – 2x + x – 1 = 0
⇒ 2x(x – 1) + 1 (x – 1) = 0
⇒ (x – 1) (2x + 1) = 0
यदि x – 1 = 0, तो x = 1
और यदि 2x + 1 = 0, तो x = – \(\frac{1}{2}\)
अतः 1 और – \(\frac{1}{2}\) व्यंजक p(x) के अन्य दो गुणनखंड है।

प्रश्न 14.
बहुपद 2x³ – 3x² + 6x + 7 में कम-से-कम क्या जोड़ा जाए कि प्राप्त बहुपद x² – 4x + 8 से पूर्णतया विभाजित हो जाए?
हल :
माना p(x) = 2x³ – 3x² + 6x + 7
और q(x) = x² – 4x + 8
अब p(x) को q(x) से भाग देने पर

यहाँ शेषफल 10x – 33 प्राप्त होता है। यदि 2x³ – 3x² + 6x +7 में 10x – 33 घटा दिया जाए तो जो बहुपद प्राप्त होगा वह q(x) से पूर्णतया विभाजित हो जाएगा।

प्रश्न 15.
यदि α तथा β बहुपद f(x) = 5x² – 7x + 1 के शून्यक है, तो (\(\frac{α}{β}=\frac{β}{α}\)) का मान ज्ञात कीजिए।
हल :
दिया, f (x)= 5x² – 7x + 1

प्रश्न 16.
k के किस मान के लिए, बहुपद
f(x) = 3x⁴ – 9x³ + x² + 15x + k,
माना, g(x) = 3x² – 5
g(x) से f(x) को भाग करने पर,

∵ f(x), g(x) से पूर्णतया विभाजित होता है, इसलिए शेषफल को शून्य के बराबर रखने पर,
k + 10 = 0
k = – 10

प्रश्न 17.
3x³ + 10x² – 9x – 4 के सभी शून्यक ज्ञात कीजिए यदि इसका एक शून्य 1 है।
हल :
दिया गया बहुपद है –
3x³ + 10x² – 9x – 4
माना, इस बहुपद के शून्यक α, β तथा γ है तथा α = 1 है।
दिए गए समीकरण को, ax³ + bx² + cx + d = 0 से तुलना करने पर प्राप्त होता है,
a = 3 b = 10, c = – 9 तथा d = – 4

⇒ 3β² + 4 = – 13β
⇒ 3β² + 13β + 4 = 0
⇒ 3β² + 12β + β + 4 = 0
⇒ 3β(β + 4) + 1(β + 4) = 0
⇒ (β + 4) (3β + 1) = 0
β = – 4 या β = \(\frac{-1}{3}\)
तब समीकरण (ii) से,
βγ = \(\frac{4}{3}\)
– 4 × γ = \(\frac{4}{3}\) या – \(\frac{1}{3}\) × γ = \(\frac{4}{3}\)
γ = –\(\frac{1}{3}\)
γ = – 4
अतः इसके शून्यक 1, – 4, – \(\frac{1}{3}\) या 1, – \(\frac{1}{3}\), – 4 होंगे।

प्रश्न 18.
p का यह मान ज्ञात कीजिए जिसके लिए बहुपद px² – 14x + 8 = 0 का एक शून्यक दूसरे का 6 गुना है।
हल :
दिया गया समीकरण है
px² – 14x + 8 = 0
माना, एक मूल = α
दूसरा मूल = 6α
मूलों का योग = – \(\frac{b}{a}\)
α + 6α = \(\frac{-(-14)}{p}\)
7α = \(\frac{14}{p}\)
α = \(\frac{14}{p \times 7}\)
α = \(\frac{2}{p}\) ……(i)
मूलों का गुणनफल = \(\frac{c}{a}\)
(α) (6α) = \(\frac{8}{p}\)
6α² = \(\frac{8}{p}\) ……(ii)
α का मान समीकरण (ii) में रखने पर,
6(\(\frac{2}{p}\))² = \(\frac{8}{p}\)
⇒ 6 × \(\frac{4}{p^2}\) = \(\frac{8}{p}\)
⇒ 24p = 8p²
⇒ 8p² – 24p = 0
⇒ 8p (p – 3) = 0
⇒ 8p = 0 ⇒ p = 0
या p – 3 = 0 ⇒ p = 3
p = 0 दिए द्विघात समीकरण px² – 14x + 8 = 0 की सन्तुष्ट नहीं करती है।
अत: p = 3

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क)

1. बहुपद में चर राशि की उच्चतम घात वाले पद के घातांक को बहुपद की …………… कहते हैं।
2. …………… बहुपद की कोई घात नहीं होती है।
3. यदि ग्राफ x-अक्ष के दो भिन्न बिन्दुओं पर काटता है, तो बहुपद के ……………. शून्यक होते हैं।
4. 1 घात के बहुपद के अधिकतम …………………. वास्तविक शून्यक हो सकते हैं।
5. ऐसे बहुपद जिसमें चर राशि की उच्चतम घात 1 हो, …………….. बहुपद कहलाते हैं।

हल:

1. घात,
2. शून्य,
3. दो,
4. 1,
5. रैखिक ।

निम्न में सत्य / असत्य बताइए :

प्रश्न (ख)

1. ऐसे बीजीय व्यजंक जिनमें चर राशियों की घात धनात्मक, ऋणात्मक अथवा शून्य हो, बहुपद कहलाते हैं।
2. बहुपद 5y³ + 2y² + 4y⁵ + y + 7 की घात 3 है।
3. बीजीय व्यंजक \(\frac{3}{4}\)x³ – \(\frac{5}{4}\)x² + 2x – 5 चर x का परिमेय संख्याओं पर बहुपद है।
4. ऐसे बहुपद को, जिसमें चर राशि की उच्चतम घात 2 हो विघातीय बहुपद कहलाता है।
5. यदि कोई व्यजंक f(x), x में बहुपद है, तब एक वास्तविक संख्या, बहुपद (x) का शून्यक कहलाती है, यदि और केवल यदि (k) = 0 हो ।

हल :

1. असत्य,
2. असत्य,
3. सत्य,
4. असत्य,
5. सत्य ।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
यदि द्विघात बहुपद x² + 3x + k का एक शून्यक 2 है, तो k का मान है:
(A) 10
(B) – 10
(C) – 7
(D) – 2
हल :
माना p(x) = x² + 3x + k
∵ 2, p(x) का एक शून्यक है।
∴ p(2) = 0
⇒ (2)² + 3(2) + k = 0
⇒ 4 + 6 + k = 0
⇒ k = – 10
अत: सही विकल्प (B) है।

प्रश्न 2.
वह द्विघात बहुपद जिसके तथा गुणनफल 6 है, है :
(A) x² + 5x + 6
(B) x² – 5x + 6
(C) x² – 5x – 6
(D) – x² + 5x + 6
हल :
बहुपद = x² – (शून्यकों का योग)x + शून्यकों का गुणनफल
= x² – (- 5)x + 6
= x² + 5x + 6
अत: सही विकल्प (A) है।

प्रश्न 3.
निम्न आकृति में, बहुपद p(x) का आलेख दिया है। बहुपद के शून्यकों की संख्या है।

(A) 1
(B) 2
(C) 3
(D) 0
हल :
∵ बहुपद का आलेख x अक्ष को दो बिन्दुओं पर काटता है।
∴ बहुपद के दो शून्यक हैं।
अतः सही विकल्प (B) है।

प्रश्न 4.
बहुपद p(x) को x² – 4 से विभाजित करने पर भागफल तथा शेषफल क्रमशः x तथा 3 पाए गए। बहुपद p(x) है:
(A) 3x² + x – 12
(B) x³ – 4x + 3
(C) x² + 3x – 4
(D) x³ – 4x – 3
हल :
∵ भाज्य = भागफल × भाजक + शेषफल
p(x) = x × (x² – 4) + 3
= x³ – 4x + 3
अत: सही विकल्प (D) है।

प्रश्न 5.
ऐसे बहुपद जिनके शून्यक केवल 3 तथा 4 हैं, की घात है :
(A) 2
(B) 1
(C) 3 से अधिक
(D) 3
हल :
ऐसा बहुपद जिसके दो शून्यक होते हैं, द्विघातीय बहुपद होता है।
अत: सही विकल्प (A) है।

प्रश्न 6.
यदि α और β बहुपद x² + 2x + 1 के शून्यक हैं, तो \(\frac{1}{\alpha}+\frac{1}{\beta}\) बराबर है।
(A) – 2
(B) 2
(C) 0
(D) 1
हल :
दिया है, बहुपद = x² + 2x + 1
∴ α + β = \(\frac{-b}{a}=\frac{-2}{1}\) = – 2
और αβ = \(\frac{c}{a}=\frac{c}{a}=\frac{1}{1}\) = 1
अब \(\frac{1}{\alpha}+\frac{1}{\beta}\) = \(\frac{\beta+\alpha}{\alpha \beta}\) = \(\frac{-2}{1}\) = – 2
अत: सही विकल्प (A) है।

प्रश्न 7.
यदि बहुपद (3x² + 8x + k) का एक शून्यक दूसरे का व्युत्क्रम है, तो k का मान है :
(A) 3
(B) – 3
(C) \(\frac{1}{3}\)
(D) \(\frac{-1}{3}\)
हल :
दिया है,
बहुपद = 3x² + 8x + k
माना एक शून्यक α है, तब दूसरा शून्यक α होगा।
शून्यकों का गुणनफल = \(\frac{c}{a}\)
⇒ α × \(\frac{1}{α}\) = \(\frac{k}{3}\)
⇒ 1 = \(\frac{k}{3}\)
⇒ k = 3
अत: सही विकल्प (A) है।

प्रश्न 8.
एक तीन घात वाले बहुपद के शून्यकों की अधिकतम संख्या है :
(A) 1
(B) 4
(C) 2
(D) 3
हल :
किसी बहुपद के शून्यकों की अधिकतम संख्या उसके घात के बराबर होती है।
अत: सही विकल्प (D) है।

प्रश्न 9.
यदि बहुपद kx² + 2x + 3 के शून्यकों का योग उनके गुणनफल के बराबर है, तो k बराबर है:
(A) \(\frac{1}{3}\)
(B) \(\frac{-1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{-2}{3}\)
हल :
शून्यकों का योग = \(\frac{-b}{a}=\frac{-2}{k}\)
शून्यकों का गुणनफल = \(\frac{c}{a}=\frac{3 k}{k}\) = 3
प्रश्नानुसार,
शून्यकों का योग = शून्यकों का गुणनफल
⇒ \(\frac{-2}{k}\) = 3
⇒ k = \(\frac{-2}{3}\)
अत: सही विकल्प (D) है।

प्रश्न 10.
द्विघात समीकरण x² + 99x + 127 के शून्यक होंगे:
(A) दोनों धनात्मक
(B) दोनों ऋणात्मक
(C) एक धनात्मक और एक ऋणात्मक
(D) दोनों समान।
हल :
∵ a > 0, b > 0 तथा c > 0 तब दोनों शून्यक ऋणात्मक होते हैं। अतः विकल्प (B) सही है।

प्रश्न 11.
चित्र में बहुपद f(x) = ax² + bx + c का आलेख दर्शाया गया हो तो :

(A) a > 0, b > 0 तथा c > 0
(B) a > 0 b < 0 तथा c < 0
(C) a > 0, b < 0 तथा c > 0
(D) a > 0, b > 0 तथा c < 0.
हल :
विकल्प (B) सही है।

प्रश्न 12.
चित्र में बहुपद f (x) = ax² + bx + c का आलेख दर्शाया गया हो तो :

(A) a < 0, b < 0 तथा c > 0
(B) a < 0, b < 0 तथा c < 0
(C) a < 0, b > 0 तथा c > 0
(D) a < 0, b > 0 तथा c < 0.
हल :
विकल्प (A) सही है।

प्रश्न 13.
त्रिघात बहुपद ax³ + bx² + cx+ d के दो शून्यक 0 दिए हैं। तीसरा शून्यक है:
(A) \(\frac{-b}{a}\)
(B) \(\frac{b}{a}\)
(C) \(\frac{c}{a}\)
(D) \(\frac{-d}{a}\)
हल :
बहुपद ax³ + bx² + cx + d के दो शून्यक 0 हैं। माना कि तीसरा शून्यक α है।
अतः शून्यकों का योग = α + 0 + 0 = \(\frac{-b}{a}\)
= α = \(\frac{-b}{a}\)
अंत: विकल्प (A) सही है।

प्रश्न 14.
यदि a – b, a तथा a + b बहुपद x³ – 3x² + x + 1 के शून्यक हैं तो (a + b) का मान होगा :
(A) 1 ± \(\sqrt{2}\)
(B) – 1 ± \(\sqrt{2}\)
(C) – 1 – \(\sqrt{2}\)
(D) 3
हल :
शून्यकों का योगफल = – \(\frac{b}{a}\)
⇒ a – b + a + a + b = \(\frac{-(-3)}{1}\)
⇒ 3a = 3
⇒ a = 1
तथा (a – b)a + a(a + b) + (a + b) (a – b) = \(\frac{c}{a}\)
⇒ (1 – b) × 1 + 1(1 + b) + (1 + b) (1 – b) = \(\frac{1}{1}\)
⇒ 1 – b + 1 + b + 1 – b² = 1
⇒ 3 – b² = 1
⇒ b² = 2
⇒ b = ± \(\sqrt{2}\)
अब a + b = 1 ± \(\sqrt{2}\)
अतः सही विकल्प (A) है।

प्रश्न 15.
यदि बहुपद f(x) = x² – 5x + k के शून्यक α तथा β इस प्रकार हों कि α – β = 1 तो k की मान होगा:
(A) 6
(B) 4
(C) 3
(D) शून्य।
हल :
बहुपद x² – 5x + k के शून्यक α, β हों तो
α + β = – (\(\frac{-5}{1}\)) = 5
αβ = \(\frac{k}{1}\) = k
अब α – β = 1
या (α – β)² = 1
या (α + β)² – 4αβ = 1
या 25 – 4k = 1
या 24 = 4k
∴ k = 6
अत: विकल्प (A) सही है।

Students should go through these JAC Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

भूमिका :
पिछली कक्षाओं में हमने समान्तर चतुर्भुअत : समचतुर्भुज तथा वर्ग के परिमाप तथा क्षेत्रफल के बारे में पढ़ा था। इस अध्याय में हम प्रारम्भ में वृत्त के परिमाप तथा क्षेत्रफल का पुनरावलोकन करेंगे तथा त्रिज्यखण्ड, वृत्तखण्ड का क्षेत्रफल ज्ञात करने के बारे में सीखेंगे। हम वृत्तों के भागों तथा वृत्तों से सम्बद्ध समतल आकृतियों के कुछ संयाजनों के क्षेत्रफलों के बारे में भी अध्ययन करेंगे।
→ वृत्त (Circle) : वृत्त एक ऐसे बिन्दु का बिन्दु पथ है जो एक समतल में एक नियत बिन्दु से सदैव समान (अचर) दूरी पर गति करता है।
→ केन्द्र (Centre) : निश्चित बिन्दु को वृत्त का केन्द्र (O) कहते हैं।
→ त्रिज्या (Radius) : एक रेखाखण्ड जो वृत्त पर एक बिन्दु तथा इसके केन्द्र को जोड़ती है. त्रिज्या कहलाती है।
→ व्यास (Diameter) : केन्द्र से होकर गुजरने वाली जीवा जिसके अन्तः बिन्दु वृत्त पर होते हैं, वृत्त का व्यास कहलाता है।
व्यास = 2 × त्रिज्या
→ जीवा (Chord) : वृत्त पर दो बिन्दुओं को जोड़ने वाले रेखाखण्ड को वृत्त की जीवा कहते हैं।
→ चाप (Arc) : वृत्त पर दो बिन्दुओं के बीच की दूरी को वृत्त का चाप कहते हैं।
→ वृत्तीय क्षेत्र (Circular region) : वह क्षेत्र जिसमें सभी बिन्दु या तो वृत्त पर या वृत्त के अन्दर स्थित होते हैं वृत्तीय क्षेत्र कहलाता है।
→ अर्द्धवृत्तीय क्षेत्र (Semi circular region) : जब दो चाप बराबर होते हैं तब प्रत्येक एक अर्द्धवृत्त होता है तथा दोनों वृत्तखण्ड व त्रिज्यखण्ड बराबर होते हैं और प्रत्येक को अर्द्धवृत्तीय क्षेत्र से जाना जाता है।
→ संकेन्द्रीय वृत्त (Concentric Circles) : ऐसे दो या दो से ज्यादा वृत्त जिनका केन्द्र समान हो तथा त्रिज्याएँ विभिन्न हों, संकेन्द्रीय वृत्त कहलाते हैं।

वृत्त का परिमाप और क्षेत्रफल – एक समीक्षा
वृत्त की परिधि (Circumference of Circle) :
वृत्त का एक चक्कर लगाने पर तय की गई दूरी को वृत्त का परिमाप या परिधि कहते हैं। किसी भी वृत्त की परिधि और व्यास का अनुपात एक निश्चित अचर राशि होती है। इस अनुपात की अचर राशि को ग्रीक अक्षर π द्वारा प्रदिर्शित करते हैं।

अतः π = परिधि / व्यास
परिधि = π × व्यास
= π × 2 = 2πr
वृत्त की परिधि = 2πr
व्यवहार में π का मान प्रायः \(\frac{22}{7}\) अथवा 3.14 लिया जाता है परन्तु π एक अपरिमेय संख्या है जिससे इसका दशमलव अनावर्ती और असान्त है। आर्यभट्ट ने इसका मान 3.1416 ज्ञात किया था जो दशमलव के 4 स्थानों तक शुद्ध है।

वृत्त का क्षेत्रफल (Area of Circle) :

वृत्त का क्षेत्रफल = \(\frac{1}{2}\) × r × (वृत्त की परिधि)
= \(\frac{1}{2}\) × r × (2πr) = πr²
अतः वृत्त का क्षेत्रफल = π(त्रिज्या)²
वृत्त का व्यास वृत्त को दो समान भागों में विभाजित करता है। अतः
अर्द्धवृत्त का परिमाप = πr + 2r
अर्द्धवृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr²

वलयिका का क्षेत्रफल (Area of an Annullus) :

चित्र में, एक वलयिका का केन्द्र O है और जिसकी बाह्य और अन्तः त्रिज्याएँ क्रमशः r₁ और r₂ (r₁ > r₂) हैं।
वलयिका का क्षेत्रफल = दोनों वृत्तों के बीच का क्षेत्रफल
= बड़े वृत्त का क्षेत्रफल – छोटे वृत्त का क्षेत्रफल
= πr₁² – πr₂²
= π(r₁² – r₂²)
= π × (त्रिज्याओं के वर्गों का अन्तर)
अतः वलयिका का क्षेत्रफल = π(r₁² – r₂²)

त्रिज्यरखण्ड और वृत्तरखण्ड के क्षेत्रफल :
वृत्त के त्रिज्यखण्ड का क्षेत्रफल (Area of a Sector of a Circle) :
किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (Sector) कहते हैं।
चित्र में, वृत्त का एक त्रिज्यखण्ड AOB है। माना कि ∠AOB = θ है और θ < 180° जब कोण 6 का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है। जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो

चाप की लम्बाई = अर्द्धवृत्त के चाप की लम्बाई
= πr
∵ केन्द्र पर 180° कोण अन्तरित करने वाले चाप की लम्बाई = πr
∴ केन्द्र पर θ कोण अन्तरित करने वाले चाप की लम्बाई = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
इसी प्रकार, जब कोई चाप वृत्त के केन्द्र पर 180° का कोण अन्तरित करता है, तो उसके संगत त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi r^2}{2}\)
∴ वृत्त के केन्द्र पर θ कोण अन्तरित करने पर बने त्रिज्यखण्ड का क्षेत्रफल
= \(\frac{\pi r^2 \theta}{2 \times 180^{\circ}}\)
= \(\frac{\pi r^2 \theta}{360^{\circ}}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
यदि r त्रिज्या के वृत्त में कोण θ के त्रिज्यखण्ड के चाप की लम्बाई L और क्षेत्रफल A है, तो
L = \(\frac{\pi r \theta}{180^{\circ}}=2 \pi r \times \frac{\theta}{360^{\circ}}\)
और A = \(\frac{\pi r^2 \theta}{360}=\pi r^2 \times \frac{\theta}{360^{\circ}}\)
चाप की लम्बाई (L) और त्रिज्यखण्ड के क्षेत्रफल (A) में सम्बन्ध :
A = \(\frac{1}{2}\)Lr
यहाँ कोण θ को डिग्री में लेते हैं।

वृत्तखण्ड का क्षेत्रफल (Area of Segment of a Circle) :
वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है। इससे बने प्रत्येक भाग को वृत्तखण्ड कहते हैं। छोटे भाग को लघु वृत्तखण्ड तथा बड़े भाग को दीर्घ वृत्तखण्ड कहते हैं।
चित्र में, वृत्त का केन्द्र O हैं और इसकी त्रिज्या r है। जीवा PQ वृत्त को दो भागों में विभाजित करती है। हमें लघु वृत खण्ड PRQ का क्षेत्रफल ज्ञात करना है।

माना ∠POQ = θ
ΔΡΟΜ ≅ ΔQΟΜ (RHS सर्वांगसमता नियम से)
∠POM = ∠QOM = \(\frac{\theta}{2}\)
त्रिज्यखण्ड OPRQ का क्षेत्रफल = लघु वृत्तखण्ड PRQ का क्षेत्रफल + ΔPOQ का क्षेत्रफल
∴ लघु वृत्तखण्ड PRQ का क्षेत्रफल = त्रिज्यखण्ड OPRQ का क्षेत्रफल – ΔPOQ का क्षेत्रफल

यदि हम दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करना चाहें, तो वृत्त के क्षेत्रफल में से लघु वृत्तखण्ड का क्षेत्रफल घटाकर ज्ञात कर सकते हैं।
अतः दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड PRQ का क्षेत्रफल
= πr² – \(\left[\frac{\pi r^2 \theta}{360^{\circ}}-\frac{r^2}{2} \sin \theta\right]\)
∴ दीर्घ वृत्तखण्ड PSQ का क्षेत्रफल = πr² – \(\frac{r^2}{2}\left[\frac{\pi \theta}{180^{\circ}}-\sin \theta\right]\)

समतल आकृतियों के संयोजन के क्षेत्रफल (Areas of Combinations of Plane Figures) :
समतल आकृतियों के छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए निम्न सूत्रों की आवश्यकता होगी :

Students should go through these JAC Class 10 Maths Notes Chapter 11 रचनाएँ will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 11 रचनाएँ

भूमिका :
कक्षा IX में, हमने कुछ रचनाओं के बारे में सीखा था जैसे कि किसी रेखाखण्ड का लम्ब समभाजक खींचना, किसी कोण का समद्विभाजक खींचना, त्रिभुजों की रचनाएँ करना इत्यादि और उनका औचित्य भी दिया था। इस अध्याय में पिछली रचनाओं के ज्ञान का उपयोग करते हुए कुछ और रचनाओं के बारे में अध्ययन करेंगे। जैसे एक रेखाखण्ड का विभाजन, किसी त्रिभुज के समरूप दूसरे त्रिभुज की रचना, वृत्त पर स्पर्श रेखा की रचना इत्यादि।

→ रचना (Construction) : कल्पना करने और बनाने की कला।

→ समरूप आकृतियाँ (Similar figures) : ऐसी ज्यामितीय आकृतियाँ जिनका रूप (shape) समान है, परन्तु जरूरी नहीं कि आकार भी समान हो, समरूप आकृतियाँ कहलाती हैं।

→ चाप (Arc) : वक्र रेखा पर दो बिन्दुओं के बीच की दूरी चाप कहलाता है।

→ स्पर्श रेखा (Tangent) : एक सीधी रेखा जो वृत्त को सिर्फ एक बिन्दु पर स्पर्श करती है, स्पर्श रेखा कहलाती है।

→ स्पर्श बिन्दु (Point of Contact) : वह बिन्दु जिस पर स्पर्श रेखा वृत्त को स्पर्श करती है, स्पर्श बिन्दु कहलाता है।

→ संकेन्द्रीय वृत्त (Concentric circles) : यदि दो वृत्तों का केन्द्र एक हो तथा विभिन्न त्रिज्याएँ हो, संकेन्द्रीय वृत्त कहलाते हैं।

Students must go through these JAC Class 10 Science Notes Chapter 16 Management of Natural Resources to get a clear insight into all the important concepts.

JAC Board Class 10 Science Notes Chapter 16 Management of Natural Resources

→ Natural resources : The naturally occurring resources which are used by human beings for various purposes are called natural resources. Soil, water, air, forests, wildlife, coal, petroleum, etc. are the examples of natural resources.

→ In 1985, Ganga Action Plan was started for cleaning and maintaining the quality of water in the river Ganga.
The presence of faecal coliform bacteria in water indicates contamination by disease causing microorganisms.

→ There are some measurable factors which are used to quantify pollution or the quality of water.
The pH of water can be easily checked using universal indicator. Water with a pH level between 6.5-8.5 is safe for drinking.

→ Conservation is controlled utilization of natural resources for the benefit of all life forms.

→ The five R’s to save the environment are:

• Refuse : It means not to buy product that can harm the environment.
• Reduce : It means use less and save natural resources.
• Reuse : It means use things again and again instead of throwing away.
• Repurpose : It means a product can be used for other purpose, when it is no more useful for its primary and main purpose.

→ Recycle : It means the processing of things that are considered waste and turning them into useful products.

→ The concept of sustainable development encourages eco-friendly approach that meets current basic human needs. Economic development is linked to environmental conservation.

→ The natural resources need to be managed due to following reasons :

• They should last for future generation
• They should be equally distributed
• The resource are used in such a way that the environment should not be harmed.

→ Forests are important renewable natural resources. A wide range of different life forms are found there. They are biodiversity hot spots.

→ The different stakeholders in a forest are :

• People who live in or around forests
• The Forest Department of the Government
• The industrialists
• The wildlife and nature enthusiasts.

→ The Government of India has instituted an ‘Amrita Devi Bishnoi National Award for Wildlife Conservation’, in the memory of Amrita Devi Bishnoi. who in 1731 sacrificed her life along with 363 others for the protection of ‘Khejri’ trees.

→ Chipko Andolan (‘Hug the Trees Movement’) was started in early 1970 from Reni village, in Garhwal.
Chipko Andolan was the result of a grass root level effort to end the alienation of people from forests.

→ Sal forests in the Arabari forest range of Midnapore district of West Bengal were saved by the involvement of the local villagers.

→ Monoculture of pine, teak and eucalyptus in the forest area are an important source of revenue for the Forest Department, but such practise destroys biodiversity.

→ Water is a basic necessity for all terrestrial forms of life.

• Rain is a very important source of fresh water.
• Large dams can ensure the storage of adequate water mainly for irrigation and for generating electricity.
• Large dams cause social, economic and environmental problems.

→ Water harvesting means storing rainwater where it falls or storing run off water in a local areas. Dr Rajendra Singh won the Stockholm Water Prize in 2015. He is known as India’s ‘Waterman’.

→ Fossil fuels, i.e., coal and petroleum were formed from the degradation of biomass millions of years ago. Energy needs have been largely met by the reserves of coal and petroleum.

We would need to look for alternative sources of energy because coal and petroleum are exhaustible energy resources.

Students should go through these JAC Class 10 Maths Notes Chapter 10 वृत्त will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 10 वृत्त

भूमिका :
कक्षा IX में हम वृत्त से सम्बन्धित अवधारणाएँ जैसे-जीवा, वृत्तखण्ड, त्रिज्यखण्ड, चाप आदि के बारे में पढ़ चुके हैं। इस अध्याय में हम समतल में स्थित एक वृत्त तथा एक रेखा की विभिन्न स्थितियों पर विचार करेंगे।
→ अभिलम्ब (Normal): किसी वृत्त के किसी बिन्दु पर अभिलम्ब वह सरल रेखा है जो दिए गए बिन्दु से गुजरती है तथा उस बिन्दु पर स्पर्श रेखा के लम्बवत होती है।
→ सम्पूरक कोण (Supplementary angles) : यदि दो कोणों का योग 180° हो, तो वे सम्पूरक कोण कहलाते हैं।
→ अन्तः कोण (Co-interior angles) : ऐसे कोण जो तिर्यक रेखा के एक ही ओर स्थित होते हैं, अन्तः कोण कहलाते हैं।
→ समान्तर चतुर्भुज (Parallelogram) : वह चतुर्भुज जिसकी सम्मुख भुजाएँ समान्तर व बराबर होती हैं, समान्तर चतुर्भुज कहलाता है।
→ समचतुर्भुज (Rhombus ) : वह चतुर्भुज जिसकी सभी भुजाएँ बराबर होती हैं, समचतुर्भुज कहलाता है।
→ परिवृत्त (Circumscribed circle) : बहुभुज के सभी शीर्षों से होकर गुजरने वाला वृत्त परिवृत्त कहलाता है।
→ अन्तः वृत्त (Inscribed circle) : बहुभुज के अन्तर्गत खींचा जा सकने वाला वह बड़े से बड़ा वृत्त जो बहुभुज की प्रत्येक भुजा को एक बिन्दु पर छूता हो, अन्तः वृत्त कहलाता है।

छेदक रेखा और स्पर्श रेखा :
यदि एक समतल में एक वृत्त तथा कोई रेखा AB खींची जाए, तो वृत्त के सापेक्ष यह रेखा तीन स्थितियों में हो सकती है :
स्थिति I. अप्रतिच्छेदी रेखा (Non intersecting line) : रेखा AB वृत्त को स्पर्श नहीं करती है अर्थात् रेखा और वृत्त के मध्य कोई सम्बन्ध नहीं होता है। इस स्थिति में रेखा AB को वृत्त के सापेक्ष अप्रतिच्छेदी रेखा कहते हैं। जैसा कि संलग्न चित्र में दर्शाया गया है।

स्थिति II. छेदक रेखा (Secant) रेखा AB वृत्त को दो भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करती है, यह रेखा वृत्त को अधिकतम दो बिन्दुओं पर ही प्रतिच्छेद कर सकती है, क्योंकि वृत्त तीन या तीन से अधिक सरेखीय बिन्दुओं से नहीं गुजर सकता है। अतः एक ऐसी सरल रेखा जो एक वृत्त को दो भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करती है, छेदक रेखा (Secant) कहलाती है। जैसा कि संलग्न चित्र में दर्शाया गया है।

स्थिति III. स्पर्श रेखा (Tangent) : रेखा AB वृत्त को दो सम्पाती बिन्दुओं पर प्रतिच्छेद करती है, अर्थात् रेखा वृत्त को एक बिन्दु पर स्पर्श करती है। अतः एक सरल रेखा जो वृत्त को केवल एक बिन्दु पर स्पर्श करे, वृत्त की स्पर्श रेखा (Tangent) कहलाती है। वृत्त के समतल में स्पर्श रेखा और वृत्त में केवल एक बिन्दु उभयनिष्ठ होता है। यह उभयनिष्ठ बिन्दु स्पर्श बिन्दु (Point of contact) कहलाता है। जैसा कि संलग्न चित्र में दिखाया गया है।

छेदक रेखा के समान्तर स्पर्श रेखा (Tangent Parallel to Secant) : एक छेदक रेखा के समान्तर वृत्त की अधिकतम दो स्पर्श रेखाएँ खींची जा सकती हैं।

चित्र में l, m, n, o छेदक रेखाएँ हैं। AB तथा CD वृत्त पर स्पर्श रेखाएँ जो वृत्त को क्रमश: P और Q बिन्दु पर स्पर्श करती हैं।

Students should go through these JAC Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग will seemingly help to get a clear insight into all the important concepts.

JAC Board Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग

भूमिका :
इस अध्याय में हम उन विधियों के विषय में पढ़ेंगे जिनमें त्रिकोणमिति का प्रयोग हमारे आसपास के जीवन से जुड़ा होता है। त्रिकोणमिति की आवश्यकता रवगोलकी में पृथ्वी से ग्रहों और तारों की दूरियाँ परिकलित करने में होती थी। त्रिकोणमिती का प्रयोग भूगोल और नौचालन, मानचित्र बनाने और देशांतर और अक्षांश के सापेक्ष एक द्वीप की स्थिति ज्ञात करने में की जाती है।

इस अध्याय में हम अध्ययन करेंगे कि वास्तविक माप के बिना, त्रिकोणमिति का प्रयोग विभिन्न वस्तुओं की ऊँचाइयाँ और दूरियाँ ज्ञात करने में किया जाता है।

ऊंचाइयाँ और दूरियाँ :
दृष्टि रेखा (Line of sight) : प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिन्दु को मिलाने वाली रेखा को दृष्टि रेखा कहते हैं, अथवा जब हम किसी वस्तु (object) को देखते हैं, तो हमारी आँख और वस्तु को जोड़ने वाली रेखा को दृष्टि रेखा कहते हैं।

चित्र में आँख बिन्दु पर है और वस्तु की स्थिति P है। अत: OP दृष्टि रेखा होगी।

पूरक कोण (Complimentary angles) : यदि दो कोणों का योग 90° हो, तो ये कोण पूरक कोण कहलाते हैं।

आन्तरिक एकान्तर कोण (Alternate interior angles) : यदि दो रेखाओं को एक तिर्यक रेखा काटती है तो दोनों रेखाओं के अन्दर तिर्यक रेखा के विपरीत दिशा में बने कोण एकान्तर कोण कहलाते हैं, यदि दोनों रेखाएँ परस्पर समान्तर हैं, तो बने आन्तरिक एकान्तर कोण बराबर होते हैं।

उन्नयन कोण (Angle of elevation): जब कोई वस्तु, आँख से ऊपर हो, तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनता है उसे उन्नयन या उन्नतांश या उन्नति कोण कहते हैं।

चित्र में आँख बिन्दु पर है और वस्तु (object) की स्थिति P है। अतः OP दृष्टि रेखा है जो क्षैतिज रेखा OX से कोण ∠XOP बनाती है। अतः उन्नयन कोण = ∠XOP

अवनमन कोण (Angle of depression) : जब कोई वस्तु, आँख से नीचे हो, तो दृष्टि रेखा, क्षैतिज के साथ जो कोण बनता है उसे अवनमन या अवनति कोण कहते हैं।

चित्र में आँख बिन्दु पर और वस्तु (object) की स्थिति P है अतः OP दृष्टि रेखा है जो क्षैतिज रेखा OX’ से कोण X’OP बनाती है। अतः अवनमन कोण = X’OP
ऊँचाई एवं दूरी की समस्याओं को हल करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिए :
(i) सर्वप्रथम प्रश्न को ध्यानपूर्वक पढ़ने के उपरान्त चित्र बनाकर समकोण त्रिभुज का निर्माण करते हैं।
(ii) समकोण त्रिभुज में ज्ञात कोण के त्रिकोणमितीय अनुपातों (sine, cosine, tangent) आदि को ज्ञात भुजा के पदों में व्यक्त करते हैं।
(iii) चित्र में स्पष्ट है कि O का P के सापेक्ष उन्नयन कोण = P का O के सापेक्ष अवनमन कोण।

चित्र में वस्तुओं द्वारा प्रेक्षक की आंख पर अन्तरित अवनमन कोणों के उदाहरण :