Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 Circles Ex 10.6 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.6
Page-186
Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
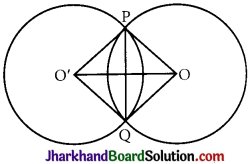
Answer:
Given: Two intersecting circles, in which OO’ is the line of centres and P and Q are two points of intersection.
To prove: ∠OPO’ = ∠OQO’
Construction: Join PO, QO, PO’ and QO’.
Proof: In APOO’ and AQOO,’
we have PO = QO [Radii of the same circle]
PO’ = QO'[Radii of the same circle]
OO’ = OO’ [Common]
APOO’ = AQOO’ [SSS axiom]
⇒ ∠OPO’ ≅ ∠OQO’ [CPCT]
Hence, the line of centres of two intersecting circles subtends equal angles at the two points of intersection. Proved.
Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
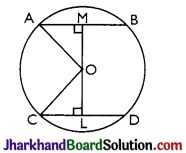
Answer:
Let O be the centre of the circle and let its radius be r cm.
Draw OM ⊥ AB and OL ⊥ CD.
Then, AM = \(\frac{1}{2}\) AB = \(\frac{5}{2}\) cm
[As perpendicular from centre to the chord bisects the chord]
Similarly, CL = \(\frac{1}{2}\) CD = \(\frac{11}{2}\) cm
Now, LM = 6 cm
Let OL = x cm.
Then OM = (6 – x) cm Join OA and OC.
Then OA = OC = r cm.
Now, from right-angled ∆OMA and ∆OLC, we have
OA2 = OM2 + AM2
and OC2 = OL2 + CL2
[By Pythagoras Theorem]
r2 = (6 – x)2 + \(\frac{5}{2}\)2
and r2 = x2 + \(\frac{11}{2}\)2
⇒ (6 – x)2 + \(\frac{5}{2}\)2 = x2 + \(\frac{11}{2}\)2
⇒ 36 +x2 – 12x + \(\frac{25}{4}\) = x2 + \(\frac{121}{4}\)
⇒ -12x = \(\frac{121}{4}\) – \(\frac{25}{4}\) – 36
⇒ -12x = \(\frac{96}{4}\) – 36
⇒ -12x = 24 – 36
⇒ -12x = -12
⇒ x = 1
Substituting x = 1 in (i), we get
r2 = (6 – x)2 + \(\frac{5}{2}\)2
r2 = (6 – 1)2 + \(\frac{5}{2}\)2
⇒ r2 = (5)2 + \(\frac{5}{2}\)2 = 25 + \(\frac{25}{4}\)
⇒ r2 = \(\frac{125}{4}\)
⇒ r = \(\frac{5 \sqrt{5}}{2}\) cm
Hence, radius r = \(\frac{5 \sqrt{5}}{2}\) cm
![]()
Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
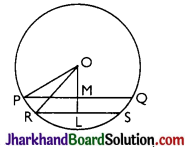
Answer:
Let PQ and RS be two parallel chord of a circle with centre O.
We have, PQ = 8 cm and RS = 6 cm.
Draw perpendicular bisector OL of RS which meets PQ of M.
Since, PQ || RS, therefore, OM is also perpendicular bisector of PQ.
Also, OL = 4 cm
RL = \(\frac{1}{2}\) RS [As perpendicular from centre to the chord bisects the chord]
= \(\frac{1}{2}\) (6)
= 3 cm
Similarly, PM = \(\frac{1}{2}\) PQ
In ORL, we have
OR2 = RL2 + OL2 [Pythagoras theorem]
⇒ OR2 = 32 + 42 = 9 + 16
⇒ OR2 = 25
⇒ OP = 5 cm
∴ OR = OP [Radii of the circle]
⇒ OP = 5 cm
Now, in ∆OPM
OM2 = OP2 – PM2 [Pythagoras theorem]
⇒ OM2 = 52 – 42 = 25 – 16 = 9
OM = \( \sqrt{9} \) = 3 cm
Hence, the distance of the other chord from the centre is 3 cm.
Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
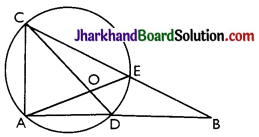
Answer:
Given: Two equal chords AD and CE of a circle with centre O meet at B when produced.
To prove: ∠ABC = \(\frac{1}{2}\) (∠AOC – ∠DOE)
Proof: Let ∠AOC = x, ∠DOE = y, and ∠AOD = ∠EOC = z [Equal chords subtends equal angles at the centre]
∴ x + y + 2z = 360° …(i)
OA = OD ⇒ ∠OAD = ∠ODA
[Angles opposite to equal sides]
∴ In ∆OAD, we have
∠OAD + ∠ODA + z = 180°
⇒ 2 ∠OAD = 180° – z [.’. ∠OAD = ∠ODA]
⇒ ∠OAD = 90° – \(\frac{z}{2}\) …(ii)
Similarly, ∠OCE = 90° – – …(iii)
⇒ ∠ODB = ∠OAD + ∠AOD
[Exterior angle property]
⇒ ∠ODB = 90° – \(\frac{z}{2}\) + z [From (ii)]
⇒ ∠ODB = 90° + \(\frac{z}{2}\) …(iv)
Also, ∠OEB = ∠OCE + ∠COE
[Exterior angle property]
⇒ ∠OEB = 90° – \(\frac{z}{2}\) + z [From (iii)]
⇒ ∠OEB = 90° + \(\frac{z}{2}\) …(v)
In ∆DOE,
OD = OE [Radii of the circle]
⇒ ∠ODE = ∠OED [Angles oposite to equal sides are equal]
Also,
∠ODE + ∠OED + ∠DOE = 180°
[Angle sum property]
⇒ ∠ODE + ∠OED + y = 180°
⇒ 2∠ODE = 180° – y
⇒ ∠ODE = 90° – \(\frac{y}{2}\)
⇒ ∠ODE = ∠OED = 90° – \(\frac{y}{2}\) …(vi)
Now, ∠BED = ∠BEO – ∠OED
= 90 + \(\frac{z}{2}\) – 90 + \(\frac{y}{2}\) [From (v) and (vi)]
= \(\frac{1}{2}\)(y + z)
Also, ∠BDE = ∠BDO – ∠ODE
= 90 + \(\frac{z}{2}\) – 90° + \(\frac{y}{2}\) [From (iv) and (vi)]
= \(\frac{1}{2}\)(y + z)
In ∆BDE,
∠BDE + ∠BED + ∠B = 180°
[Angle sum property]
=> \(\frac{1}{2}\) (y+ z) + \(\frac{1}{2}\) (y + z) + ∠ABC = 180°
⇒ y + z + ∠ABC = 180°
⇒ ∠ABC = 180 – y – z …(vii)
Consider,
\(\frac{1}{2}\)(∠AOC – ∠DOE) = \(\frac{1}{2}\)(x – y)
= \(\frac{1}{2}\)[360° – y – 2z – y] From (i)
= 180° – (y + z) …(viii)
From (vii) and (viii)
∠ABC = \(\frac{1}{2}\) (∠AOC – ∠DOE)
![]()
Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
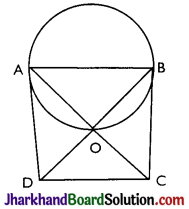
Answer:
Given: A rhombus ABCD whose diagonals intersect each other at O.
To prove: A circle with AB as diameter passes through O.
Proof: ∠AOB = 90°
[Diagonals of a rhombus bisect each other at 90°]
⇒ ∆AOB is a right triangle right angled at O.
⇒ AB is the hypotenuse of right ∆AOB.
⇒ If we draw a circle with AB as diameter, then it will pass through O because angle in semicircle is 90° and ∠AOB = 90°.
Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Answer:
Given: ABCD is a parallelogram.
To Prove: AE = AD.
Construction: Draw a circle which passes through ABC and intersect CD produced E.
Proof: As ABCD is a parallelogram,
∠B = ∠ADC …(i)
[Opposite angles of parallelogram]
Also, ∠ADC + ∠ADE = 180°
[Linear Pair]
⇒ ∠B + ∠ADE = 180° …(ii) [From (i)]
Also, ∠B + ∠E = 180° …(iii) [Opposite angles of cyclic quadrilateral]
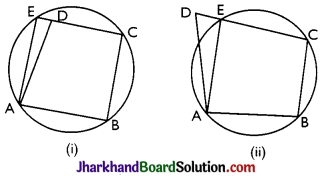
From (ii), (iii)
∠B = 180° – ∠ADE = 180° – ∠E
⇒ 180° – ∠ADE = 180° – ∠E
⇒ ∠ADE = ∠E
In ∆ADE, AD = AE [Sides opposite to equal angles]
Similarly, we can prove for fig. (ii).
Question 7.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is rectangle.
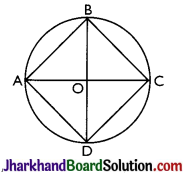
Answer:
Given: A circle with chords AC and BD which bisect each other at O.
To Prove: (i) AC and BD are diameters (ii) ABCD is a rectangle.
Proof: In ∆OAB and ∆OCD, we have
OA = OC [Given]
OB = OD [Given]
∠AOB = ∠COD
[Vertically opposite angles]
∠∆AOB = ∆COD [SAS congruence]
∠ABO = ∠CDO [CPCT]
and angles ∠ABO, ∠CDO are alternate interior angles
∴ AB || DC …(i)
Similarly, we can prove BC || AD …(ii)
Hence, ABCD is a parallelogram.
[As opposite sides are parallel]
⇒ ∠A = ∠C [Opposite angles of parallelogram]
and ∠B = ∠D
Also, as ABCD is cyclic
⇒ ∠A + ∠C = 180°
[Opposite angles of cyclic quadrilateral]
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
So, ABCD is a parallelogram in which one angle is 90°
⇒ ABCD is a rectangle
⇒ ∠ABC = 90° and ∠BCD = 90°.
⇒ AC and BD are diameters.
![]()
Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are
90° – \(\frac{1}{2}\) A, 90° – \(\frac{1}{2}\) B and 90° – \(\frac{1}{2}\) C.
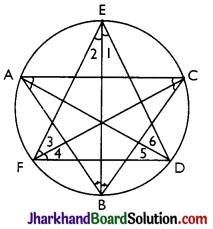
Answer:
Given: AABC and its circumcircle. AD, BE, CF are bisectors of ∠A, ∠B, ∠C respectively.
Construction: Join DE, EF and FD.
Proof: We know that angles in the same segment are equal.
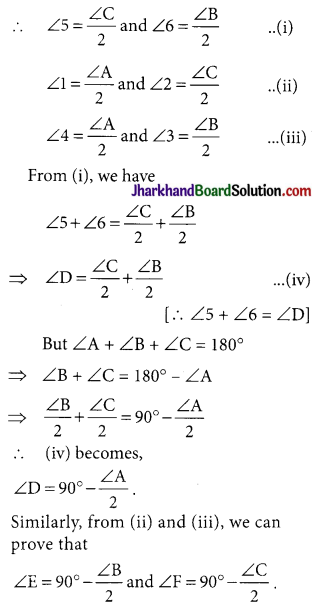
Page-187
Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
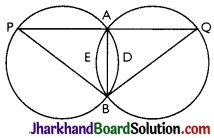
Answer:
Given: Two congruent circles which intersect at A and B. PAQ is a line through A.
To Prove: BP = BQ.
Construction: Join AB.
Proof: AB is a common chord of both the circles.
As the circles are congruent,
arc ADB = arc AEB
⇒ ∠APB = ∠AQB [Angles subtended by equal arcs]
So, in APBQ, BP = BQ [Sides opposite to equal angles are equal]
Question 10.
If any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.

Answer:
(i) Let bisector of ∠A meet the circumcircle of ∆ABC at M.
Join BM and CM.
∴ ∠MBC = ∠MAC [Angles in same segment]
and ∠BCM = ∠BAM [Angles in the same segment]
But ∠BAM = ∠CAM [∴ AM is bisector of ∠A]
∴ ∠MBC = ∠BCM So, MB = MC [Sides opposite to equal angles are equal].
⇒ M lies on the perpendicular bisector of BC
Hence, angle bisector of ∠A and perpendicular bisector of BC intersect on the circumcircle of ∆ABC.
(ii) Let M be a point on the perpendicular bisector of BC which lie on circumcircle of ∆ABC
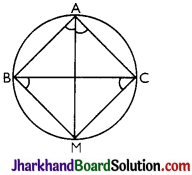
Join AM,
∴ M lies on perpendicular bisector of BC.
∴ BM = CM
∠MBC = ∠MCB [Angle opposite to equal sides are equal]
But ∠MBC = ∠MAC [Angles in the same segment]
and ∠MCB = ∠BAM [Angles in the same segment]
So, from (i)
∠BAM = ∠CAM AM is bisector of ∠A
⇒ bisector of ∠A and perpendicular bisector of BC intersect at M which lies on circumcircle of ∆ABC.