Jharkhand Board JAC Class 9 Maths Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 11 Constructions Ex 11.1
Page-191
Question 1.
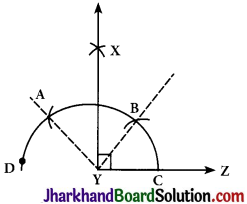
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Answer:
Steps of construction:
Step 1: A ray YZ is drawn.
Step 2: With Y as a centre and any radius, an arc CD is drawn cutting YZ at C.
Step 3: With C as a centre and the same radius, mark a point B on the arc ABC. Step 4: With B as a centre and the same radius, mark a point A on the arc CD. Step 5: With A and B as centres, draw two arcs intersecting each other with the same radius at X.
Step 6: X and Y are joined and a ray YX making an angle 90° with YZ is formed.
Justification for construction:
We constructed ∠BYZ = 60° and also ∠AYB = 60°.
Thus, ∠AYZ = 120°.
Also, bisector of ∠AYB is constructed such that:
∠AYB = ∠XYA + ∠XYB
⇒ ∠XYB = \(\frac{1}{2}\) ∠AYB (∠XYA = ∠XYB as XY bisects ∠AYB)
⇒ ∠XYB = \(\frac{1}{2}\) × 60°
⇒ ∠XYB = 30°
Now,∠XYZ = ∠BYZ + ∠XYB
= 60° + 30° = 90°
![]()
Question 2.
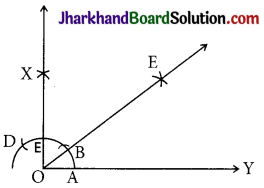
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Answer:
Steps of construction:
Step 1: A ray OY is drawn.
Step 2: With O as a centre and any radius, an arc AD is drawn cutting OY at A.
Step 3: With A as a centre and the same ‘ radius, mark a point B on the arc AC.
Step 4: With B as a centre and the same radius, mark a point C on the arc AD.
Step 5: With C and B as centres, draw two arcs intersecting each other with the same radius at X.
Step 6: X and O are joined and a ray making an angle 90° with OY is formed.
Step 7: With A and E as centres, two arcs are marked intersecting each other at E and the bisector of ∠XOY is drawn such that ∠EOY = 45°.
Justification for construction:
By construction,
∠XOY = 90°
We constructed the bisector of ∠XOY as ∠EOY.
Thus,
∠EOY = \(\frac{1}{2}\) ∠XOY
ZEOY = \(\frac{1}{2}\) × 90° = 45°
![]()
Question 3.
Construct the angles of the following measurements:
(i) 30° (ii) 22.5° (iii) 15°
Answer:
(i) 30°
Steps of construction:
Step 1 : A ray OY is drawn.
Step 2: With O as a centre and any radius, an arc AC is drawn cutting OY at A.
Step 3: With A as centre and the same radius, mark a point B on arc AC.
Step 4: With A and B as centres, two arcs are marked intersecting each other at X and join OX.
Thus, Z∠XOY is the required angle making 30° with OY.
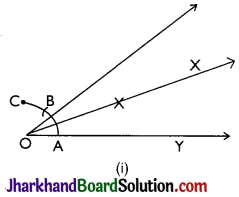
(ii) 22.5°
Steps of construction:
Step 1: An angle ∠XOY = 90° is drawn.
Step 2: Bisector of ∠XOY is drawn such that ∠BOY = 45° is constructed.
Step 3: Again, ∠BOY is bisected such that ∠AOY is formed.
Thus, ∠AOY is the required angle making 22.5° with OY.
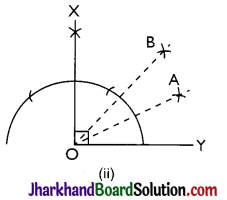
![]()
(iii) 15°
Steps of construction:
Step 1: An angle ∠AOY = 60° is drawn.
Step 2: Bisector of ∠AOY is drawn such that ∠BOY = 30° is constructed.
Step 3: With C and D as centres, two arcs are marked intersecting each other at X and the bisector of ∠BOY is drawn.
Thus, ∠XOY is the required angle making 15° with OY.
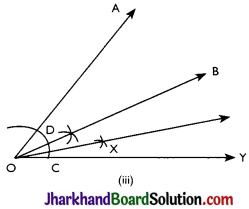
Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75° (ii) 105° (iii) 135°
Answer:
(i) 75°
Steps of construction:
Step 1: A ray OY is drawn.
Step 2: An arc BAE is drawn with O as a centre and OE as radius.
Step 3: With E as a centre, and the same radius, mark point A on the arc BAE.
Step 4: With A as centre and the same radius, mark a point C on the arc BAE.
Step 5: With A and C as centres, arcs are made to intersect at X and ∠XOY = 90° is made.
Step 6: With A and F as centres, arcs are made to intersect at D.
Step 7: OD is joined and and ∠DOY = 75° is constructed.
Thus, ∠DOY is the required angle making 75° with OY.
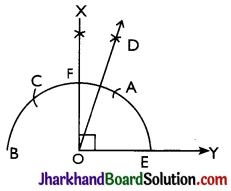
![]()
(ii) 105°
Steps of construction:
Step 1: A ray OY is drawn.
Step 2: An arc is drawn with O as a centre.
Step 3: With E as a centre and the same radius mark point A on the arc BAE.
Step 4: With A as centre and the same radius, mark a point C on the arc BAE.
Step 5: With A and C as centres, arcs are made to intersect at D and ∠DOY = 90° is made. Join DO to intersect EAC at M.
Step 6: With C and M as centres, arcs are made to intersect at X.
Step 7: OX is joined and and ∠XOY = 105° is constructed.
Thus, ∠XOY is the required angle making 105° with OY.
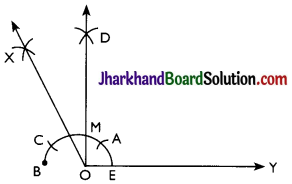
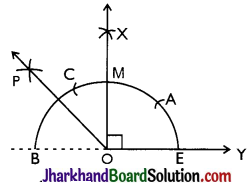
(iii) 135°
Steps of construction:
Step 1: A ray OY is drawn.
Step 2: An arc is drawn with O as a centre to intersect OY at E and YO produced to B.
Step 3: With E as a centre and the same radius mark point A on the arc BAE.
Step 4: With A as centre and the same radius, mark a point C on the arc BAE.
Step 5: With A and C as centres, arcs are made to intersect at X and ∠XOY = 90° is made.
Step 6: With M and B as centres, arcs are made to intersect at P or bisector of ∠XOB is constructed.
Step 7: OP is joined and ∠POY = 135° is constructed.
![]()
Question 5.
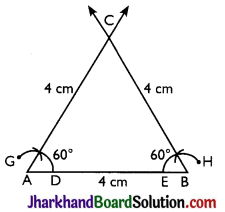
Construct an equilateral triangle, given its side and justify the construction.
Ans. Steps of construction:
Step 1: A line segment AB = 4 cm is drawn.
Step 2: With A and B as centres, two arcs DG and EH are made.
Step 3: With D and E as centres, arcs with previous radius are made to cut the previous arcs respectively and forming angle of 60° each.
Step 4: Lines from A and B are extended to meet each other at C.
Thus, ABC is the required triangle formed.
Justification:
By construction,
AB = 4 cm, ∠A = 60° and ∠B = 60° We know that,
∠A + ∠B + ∠C = 180° (Sum of the angles of a triangle)
⇒ 60° + 60° + ∠C = 180°
⇒ 120° + ∠C = 180°
⇒ ∠C = 60°
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm ∠A = ∠B = ∠C = 60°