Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4
Page-164
Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
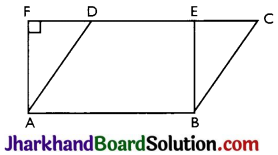
Answer:
In ∆AFD,
∠F = 90° [Each angle of a rectangle is equal to 90°]
∠F + ∠A + ∠D = 180°
(Angle sum property)
⇒ 90° + ∠A + ∠D = 180°
⇒ ∠A + ∠D = 180° – 90° = 90°
⇒ ∠D < 90° ( v ∠F = 90°)
⇒ ∠D < ∠F
⇒ AF < AD [Since side opposite to larger angle is longer] Adding AB to both the sides AD + AB > AF + AB
Multiplying by 2
2 [AD + AB] > 2 [AF + AB]
⇒ Perimeter of the parallelogram ABCD > Perimeter of the Rectangle ABEF.
Question 2.
In Figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
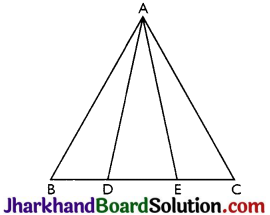
Answer:
In ∆ABE, AD is median [∵ BD = DE]
So, ar (ABD) = ar (AED) ………..(i)
[∵ Median of a triangle divides it into two parts of equal areas.]
Similarly,
In ∆ADC, AE is median [∵ DE = EC]
So, ar (ADE) = ar (AEC) ………..(ii)
From equations (i) and (ii), we get
ar (ABD) = ar (ADE) = ar (AEC)
![]()
Page-165
Question 3.
In figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
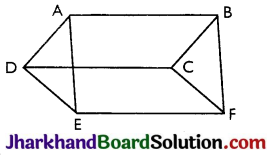
Answer:
In ∆ADE and ∆BCF,
AD = BC [∵ Opposite sides of parallelogram ABCD]
DE = CF [∵ Opposite sides of parallelogram DCFE]
AE = BF [∵ Opposite sides of parallelogram ABFE]
So, ∆ADE ≅ ∆BCF [∵ SSS Congruence theorem]
∴ ar (ADE) = ar (BCF) [∵ Congruent triangles have equal areas]
Question 4.
In Fig, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
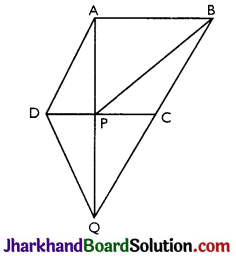
Answer:
In ∆ADP and ∆QCP,
∠APD = ∠QPC [∵ Vertically Opposite Angles]
∠ADP = ∠QCP [∵ Alternate angles]
AD = CQ [∵ Given]
So, ∆APD ≅ ∆CPQ [∵ AAS Congruence theorem]
So, DP = CP [∵ CPCT]
In ∆CDQ, QP is median. [∵ DP = CP]
So, ar (DPQ) = ar (QPC) …(i)
[∵ Median of a triangle divides it into two parts of equal areas.]
Similarly,
In ∆PBQ, PC is median.
[∵ AD = CQ and AD = BC ⇒ BC = QC]
So, ar (QPC) = ar (BPC) …(ii)
From equations (i) and (ii), we get
ar (BPC) = ar (DPQ)
Question 5.
In Figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
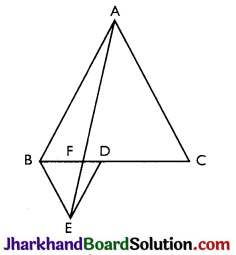
(i) ar (BDE) = \(\frac{1}{4}\) ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\) ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\) ar (AFC)
[Hint: Join EC and AD. Show that BE 11 AC and DE|| AB, etc.]
Answer:
(i) Construction: Join EC and AD
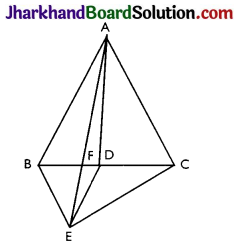
Let, BC = x
So, ar(∆ABC) = \(\frac{\sqrt{3}}{4}\) x2
[∵ Area of a equilateral triangle = \(\frac{\sqrt{3}}{4}\) (Side)2
and ar (∆BDE) = \(\frac{\sqrt{3}}{4}\left(\frac{x}{2}\right)^2\)
[∵ D is the mid-point of BC]
= \(\frac{1}{4}\) [\(\frac{\sqrt{3}}{4}\) x2] = \(\frac{1}{4}\) [ar(AABC)]
![]()
(ii) In ∆BEC, ED is median
[∵ D is the mid-point of BC]
So, ar (BDE) = \(\frac{1}{2}\) ar (∆BEC) …(i)
[∵ Median of a triangle divides it into two parts of equal areas.]
∠EBC = 60° and ∠BCA = 60°
[∵ Angles of equilateral triangle]
So, ∠AEBC = ∠BCA
Since, alternate angles (∠EBC = ∠BCA) are equal, so BE || AC
Triangles BEC and BAE are on the same base BE and between same parallels BE || AC
So, ar (∆BEC) = ar (∆BAE) …(ii)
[∵ Triangles on the same base and between same parallels are equal in area]
From equation (i) and (ii), we get
So, ar (∆BDE) = \(\frac{1}{2}\) ar (∆BAE)
(iii) In ∆BEC, ED is median
[∵ D is the mid-point of BC]
So, ar (∆BDE) = \(\frac{1}{2}\) ar (∆BEC) …(iii)
[∵ Median of a triangle divides it into two parts of equal areas.]
ar (∆BDE) = \(\frac{1}{2}\) ar (∆ABC) ………..(iv)
[∵ Proved in (i)]
From the equations (iii) and (iv), we get
ar (∆ABC)= 4 ar (∆BDE) = 4 (\(\frac{1}{2}\)) ar(∆BEC) = 2 ar (∆BEC)
(iv) ∠ABD = 60° and ∠BDE = 60°
[∵ Angles of equilateral triangle]
So, ∠ABD = ∠BDE
Since, alternate angles (∠ABD = ∠BDE) are equal, so BA || ED Triangles BDE and AED are on the same base ED and between same parallels BA || ED.
So, ar (∆BDE) = ar (∆AED)
[∵ Triangles on the same base and betwee same parallels are equal in area]
Subtracting ar (∆FED) from both the sides
ar (∆BDE) – ar (∆FED) = ar (∆AED) – ar (∆FED)
⇒ ar (∆BEF) = ar (∆AFD)
(v) ΔADF is also right angled at D. [As in equilateral triangle, median and altitude are same]
⇒ AB2 = AD2 + BD2
⇒ AD2 = AB2 – BD2
Let AB = a and hence BD = \(\frac{a}{2}\)
(as AD is the median)
⇒ AD = \(\frac{\sqrt{3}a}{2}\)
In ΔFED,
EF2 = DE2 – DF2 = (\(\frac{a}{2}\))2 – (\(\frac{a}{4}\))2
= \(\frac{a^{2}}{4}\) – \(\frac{a^{2}}{10}\) = \(\frac{3a^{2}}{16}\)
⇒ EF = \(\frac{\sqrt{3}a}{2}\)

(vi) ar (ΔBDE) = \(\frac{1}{4}\) ar (ΔABC) [∵ From Part (i)]
⇒ ar (ΔBEF) + ar (ΔFED) = \(\frac{1}{4}\) ar (ΔABC)
⇒ ar (ΔBEF) + ar (ΔFED) = \(\frac{1}{4}\) [2 ar (ΔADC)]
[∵ ar (ΔABC) = 2 ar (ΔADC)]
⇒ 2 ar (ΔFED) + ar (ΔFED) = \(\frac{1}{2}\) ar (ΔADC) [∵ From Part (v)]
⇒ 3 ar (ΔFED) = \(\frac{1}{2}\) [ar (ΔAFC) – ar (ΔAFD)]
⇒ 3 ar (ΔFED) = \(\frac{1}{2}\) [ar (ΔAFC) – 2ar (ΔFED)] [∵ From Part (vii)]
⇒ 3 ar (ΔFED) = \(\frac{1}{2}\) ar (ΔAFC) – \(\frac{1}{2}\) × 2ar (ΔFED)
⇒ 3 ar (ΔFED) = \(\frac{1}{2}\) ar (ΔAFC) – ar (ΔFED)
⇒ 4 ar (ΔFED) = \(\frac{1}{2}\) ar (ΔAFC)
⇒ ar (ΔFED) = \(\frac{1}{8}\) ar (ΔAFC)
![]()
Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint: From A and C, draw perpendiculars to BD]
Answer:
Construction: From A and C, draw perpendiculars AM and CN to BD.
ar (ΔAPB) × ar (ΔCPD) = \(\frac{1}{2}\) × BP × AM × \(\frac{1}{2}\) × PD × CN …(i)
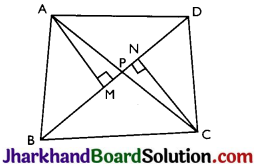
ar (ΔAPD) × ar (ΔBPC) = \(\frac{1}{2}\) × PD × AM × \(\frac{1}{2}\) × BP × CN …(ii)
From (i) and (ii), we get
ar (ΔAPB) × ar (ΔCPD) = ar (ΔAPD) × ar (ΔBPC)
Question 7.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar (PRQ) = \(\frac{1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Answer:
Construction: Join AQ, PC, RC and RQ.
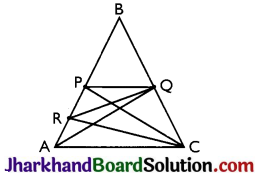
(i) In ΔAPQ, QR is median [∵ Given]
So, ar (ΔPQR) = \(\frac{1}{2}\) ar (ΔAPQ) …(i)
[∵ Median of a triangle divides it into two parts of equal areas.]
Similarly,
In ΔAQB, QP is median [∵ Given]
[∵ So, ar (ΔAPQ) = \(\frac{1}{2}\) ar (ΔABQ) ……(ii)
and in ΔABC, AQ is median [∵ Given]
So, ar (ΔABQ) = \(\frac{1}{2}\) ar (ΔABC) ……..(iii)
Form (i), (ii) and (iii), we get
ar (ΔPQR) = \(\frac{1}{2}\) ar (ΔAPQ)
= \(\frac{1}{2}\)[\(\frac{1}{2}\) ar(ΔABQ)]
= \(\frac{1}{4}\)[\(\frac{1}{2}\)ar(ΔABC)]
= \(\frac{1}{8}\) ar (ABC) ………(iv)
In ΔAPC, CR is median. [∵ Given]
So, ar (ΔARC) = \(\frac{1}{2}\) ar (APC) ……(v)
[∵ Median of a triangle divides it into two parts of equal areas.]
Similarly,
In ΔABC, CP is median [∵ Given]
So, ar (ΔAPC) = \(\frac{1}{2}\) ar (ΔABC) ……..(vi)
Form (v) and (vi), we get
ar (ΔARC) = \(\frac{1}{2}\) ar (ΔAPC)
= \(\frac{1}{2}\)[\(\frac{1}{2}\) ar(ΔABC)]
= \(\frac{1}{2}\)[\(\frac{1}{2}\) ar(ΔABC)]
= \(\frac{1}{4}\) ar(ΔABC) ……..(vii)
Form (iv) and (vii), we get
ar (ΔPQR) = \(\frac{1}{8}\) ar (ΔABC)
= \(\frac{1}{2}\)[\(\frac{1}{4}\) ar(ΔABC)]
= \(\frac{1}{2}\)[\(\frac{1}{2}\) ar(ΔABC)]
= \(\frac{1}{8}\) ar(ΔARC)
(ii) ar (∆RQC) = = ar (∆RQA) + ar (∆AQC) – ar (∆ARC) ……(viii)
In ∆PQA, QR is median [∵ Given]
So, ar (RQA) = \(\frac{1}{2}\) ar (PQA) …(ix)
In ∆AQB, PQ is median. [∵ Given]
So, ar (PQA) = \(\frac{1}{2}\) ar (AQB) …….(x)
In ABC, AQ is median [∵ Given]
So, ar (∆AQB) = \(\frac{1}{2}\) ar (∆ABC) …(xi)
From (ix), (x) and (xi), we get

(iii) In ΔABQ, PQ is median [∵ Given]
So, ar (ΔPBQ) = \(\frac{1}{2}\) ar (ΔABQ) ……..(xvii)
In ΔABC, AQ is median
So, ar (ΔABQ) = \(\frac{1}{2}\) ar (ΔABC) ……..(xviii)
Form (xvi), (xvii) and (xviii), we get
ar (ΔARC) = \(\frac{1}{4}\) ar (ΔABC)
= \(\frac{1}{4}\)[2 ar(ΔABQ)]
= \(\frac{1}{2}\) (2) ar(ΔPBQ)
= ar(ΔPBQ)
Question 8.
In the figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
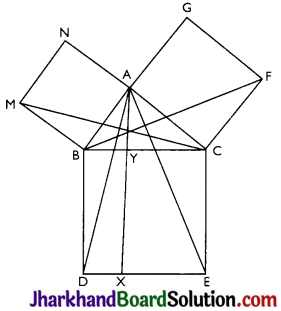
(i) ∆MBC ≅ ∆ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Answer:
(i) In ∆MBC and ∆ABD,
BC = BD [ v Sides of square]
∠MBC = ∠ABD = 90° + ∠ABC
MB = AB [∵ Sides of square]
So, ∆MBC ≅ ∆ABD
[∵ SAS Congurence theorem]
![]()
(ii) YX || BD
[Opposite sides of square are parallel]
Triangle ABD and parallelogram BYXD are on the same base BD and lie between the same parallels AX j | BD.
So, ar (AABD) = \(\frac{1}{2}\) ar (BYXD) …(i)
[∵ If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.]
But, ∆MBC ≅ ∆ABD
[∵ Proved above]
So, ar (MBC) = ar (ABD) …(ii)
From (i) and (ii), we get
ar (∆MBC) = ar (∆ABD)
= \(\frac{1}{2}\) ar (BYXD) …(iii)
⇒ 2 ar (MBC) = ar (BYXD)
(iii) MB || NA (Opposite sides of square are parallel)
Triangle MBC and square ABMN are on the same base MB and lie between the same parallels MB || NC.
So, ar (∆MBC) = \(\frac{1}{2}\) ar (ABMN)…(iv)
[∵ If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.]
From (iii) and (iv), we get
ar (BYXD) = 2 ar (MBC) = ar (ABMN)
(iv) In ∆ACE and ∆BCF,
CE = BC [∵ Sides of square]
∠ACE = ∠BCF = 90° + ∠ACB
AC = CF [∵ Sides of square]
So, ΔACE ≅ ΔBCF
[∵ SAS Congruence rule]
(v) EC || XY (Opposite sides of square are parallel)
Triangle ACE and square CYXE are on the same base CE and lie between same parallels CE || AX.
So, ar (ACE) = \(\frac{1}{2}\) ar (CYXE)
[∵ If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.]
⇒ ar (AFCB) = \(\frac{1}{2}\) ar (CYXE) …(v)
[As ΔACE ≅ ΔBCF ⇒ ar (FCB) = ar (AACE)]
⇒ 2 ar (AFCB) = ar (CYXE)
![]()
(vi) CF || AG (Opposite sides of square are parallel)
Triangle BCF and square ACFG are on the same base CF and lie between same parallels CF || FG.
So, ar (ABCF) = \(\frac{1}{2}\) ar (ACFG) …(vi)
[∵ If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.]
From (v) and (vi), we get
⇒ ac (CYXE) = 2ar (FCB)
= 2 (\(\frac{1}{2}\))ar (ACFG) = ar (ACFG)
(vii) From part (iii) and (vi), we get
ar (BYXD) = ar (ABMN)
and ar (CYXE) = ar (ACFG)
Adding both, we get
ar (BYXD) + ar (CYXE) = ar (ABMN) + ar (ACFG)
⇒ ar (BCED) = ar (ABMN)+ ar (ACFG)