Jharkhand Board JAC Class 9 Maths Solutions Chapter 3 Coordinate Geometry Ex 3.1 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 3 Coordinate Geometry Ex 3.1
Page – 54
Question 1.
How will you describe the position of a table lamp on your study table to another person?
Answer:
To describe the position of a table lamp on the study table, we have to take two lines, a perpendicular and other horizontal. Considering the table as a plane and taking perpendicular line as y-axis and horizontal as x-axis. Take one corner of table as origin where both x and y axes intersect each other. Now, the length of table is y axis and breadth is x axis. From the origin, join the line to the lamp and mark a point. Calculate the distance of this point from both x and y axes and then write it in terms of coordinates.
Let the distance of point from y-axis is x and from x-axis is y then the the position of the table lamp in terms of coordinates is (x, y).
![]()
Question 2.
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North – South direction and another in the East – West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North – South direction and 5th in the East – West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
(i) how many cross – streets can be referred to as (4, 3).
(ii) how many cross – streets can be referred to as (3, 4)
Answer:
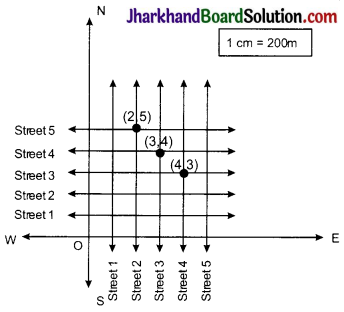
(i) Only one cross-street can be referred to as (4, 3) as we see from the figure.
(ii) Only one cross-street can be referred to as (3, 4) as we see from the figure.