Jharkhand Board JAC Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.3 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.3
Page-74
Question 1.
Draw the graph of each of the following linear equations in two variables:
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
Answer:
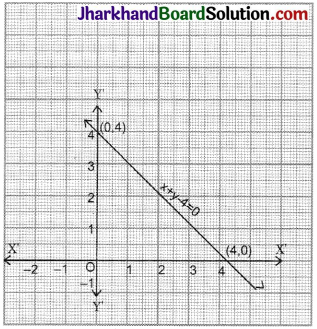
(i) x + y = 4
Put x = 0 then y = 4
Put x = 4 then y = 0
| x | 0 | 4 |
| y | 4 | 0 |
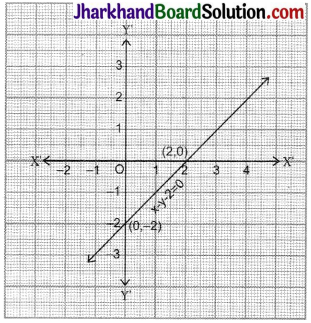
(ii) x – y = 2
Put x = 0 then y = -2
Put x = 2 then y = 0
| x | 0 | -2 |
| y | -2 | 0 |
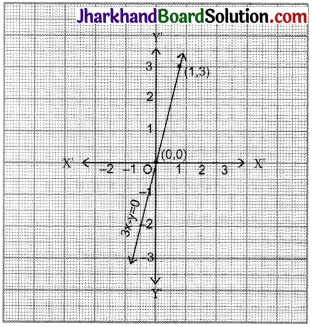
(iii) y = 3x
Put x = 0 then y = 0
Put x = 1 then y = 3
| x | 0 | 1 |
| y | 0 | 3 |
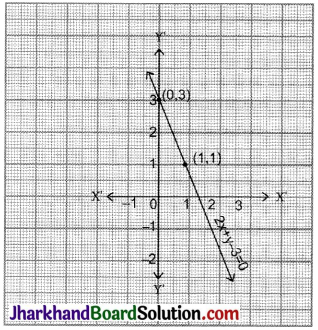
(iv) 3 = 2x + y
Put x = 0 then y =3
Put x = 1 then y = 1
| x | 0 | 1 |
| y | 3 | 1 |
![]()
Question 2.
Give the equations of two lines passing through (2, 14). How many more such lines are there, and why?
Answer:
Here, x = 2 and y = 14.
Thus, x + y = 16
also, y = 7x (∵ x = 2, y = 14)
⇒ y – 7x = 0
∴ The equations of two lines passing through (2, 14) are x + y = 16 and y – 7x = 0.
There will be infinite such lines because infinite number of lines can pass through a given point.
Question 3.
If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
Answer:
The point (3, 4) lies on the graph of the equation 3y = ax + 7.
∴ Putting x = 3 and y = 4 in the equation
3y = ax + 7, we get
3 × 4 = a × 3 + 7
⇒ 12 = 3a + 7
⇒ 3a = 12 – 7
⇒ a = \(\frac{5}{3}\)
Question 4.
The taxi fare in a city is as follows: For the first kilometre, the fare is ₹8 and for the subsequent distance it is ₹5 per km. Taking the distance covered as x km and total fare as ₹y, write a linear equation for this information, and draw its graph.
Answer:
Total fare = ₹y
Total distance covered = x kilometre
Fair for the subsequent distance after 1st kilometre = ₹5
Fair for 1st kilometre = ₹8
y = 8 + 5(x – 1)
⇒ y = 8 + 5x – 5
⇒ y = 5x + 3
| x | 0 | \(\frac{-3}{5}\) |
| y | 3 | 0 |
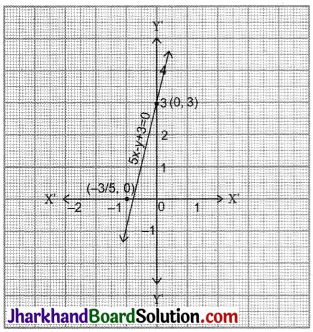
![]()
Question 5.
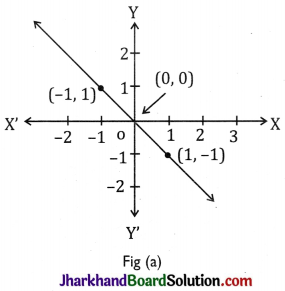
From the choices given below, choose the equation whose graphs are given in Fig (a) and Fig (b).
For Fig (a)
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
For Fig (b)
(i) y = x + 2
(ii) y = x – 2
(iii) y = -x + 2
(iv) x + 2y = 6
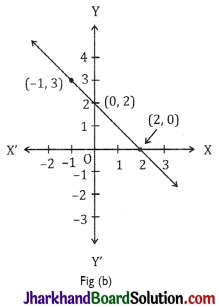
Answer:
In fig. (a), points are (0, 0), (-1, 1) and (1,-1).
∴ Equation (ii) x + y = 0 is correct as it satisfies all the values of the points.
In fig. (b), points are (-1, 3), (0, 2) and (2, 0).
∴ Equation (iii) y = -x + 2 is correct as it satisfies all the values of the points.
Page-75
Question 6.
If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body,
(i) 2 units (ii) 0 unit
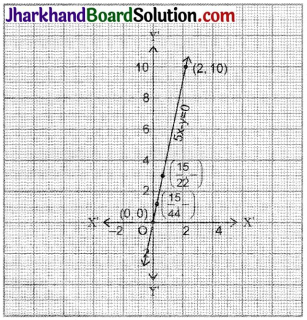
Answer:
Let the distance traveled by the body be x and y be the work done by the force.
y ∝ x (Given)
⇒ y = 5x (To equate the proportional, we need a constant).
Here, it was given 5
When x = \(\frac{1}{4}\), y = \(\frac{5}{4}\)
When x = \(\frac{1}{2}\) , y = \(\frac{5}{2}\)
| x | \(\frac{1}{4}\) | \(\frac{1}{2}\) |
| y | \(\frac{5}{4}\) | \(\frac{5}{2}\) |
(i) When x = 2 units then y = 10 units
(ii) When x = 0 unit then y = 0 unit
Question 7.
Yamini and Fatima, two students of Class IX of a school, together contributed ? 100 towards the Prime Minister’s Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You may take their contributions as ₹ x and ₹ y.) Draw the graph of the same.
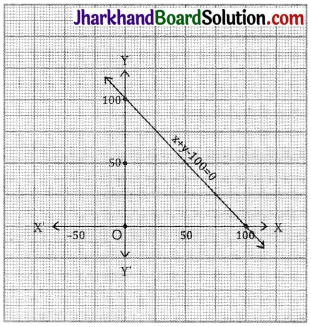
Answer:
Let the contribution amount by Yamini be ₹ x and contribution amount bv Fatima be ₹ y.
x + y = 100
When x = 0 then y = 100
When x = 50 then y = 50
When x = 100 then y = 0
| x | 0 | 50 | 100 |
| y | 100 | 50 | 0 |
Question 8.
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:
F = (\(\frac {9}{5}\))C + 32
(i) Draw the graph of the linear equation above using Celsius for x-axis and Fahrenheit for y-axis.
(ii) If the temperature is 30°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 95°F, what is the temperature in Celsius?
(iv) If the temperature is 0°C, what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
Answer:
(i) F = (\(\frac {9}{5}\))C + 32
When C = 0 then F = 32
also, when C = -10 then F = 14
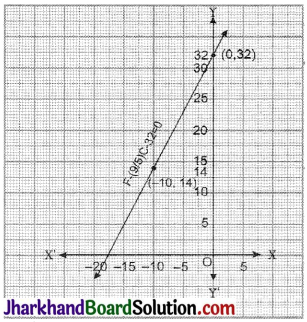
(ii) Putting the value of C = 30° in
F = (\(\frac {9}{5}\))C + 32, we get
F = \(\frac {9}{5}\) × 30 + 32
⇒ F = 54 +32
⇒ F = 86
![]()
(iii) Putting the value of F = 95 in
F = (\(\frac {9}{5}\))C + 32, we get
95 = (\(\frac {9}{5}\))C + 32
⇒ \(\frac {9}{5}\)C = 95 – 32
⇒ C = 63 × \(\frac {5}{9}\) = 35
(iv) Putting the value of F = 0 in
F = (\(\frac {9}{5}\))C + 32, we get
0 = (\(\frac {9}{5}\))C + 32
⇒ \(\frac {9}{5}\)C = – 32
⇒ C = – 32 × \(\frac {5}{9}\)
⇒ C = \(\frac{-160}{9}\)
Putting the value of C = 0 in
F = (\(\frac {9}{5}\))C + 32, we get
F = (\(\frac {9}{5}\)) × 0 + 32
⇒ F = 32
(v) Here, we have to find when F = C
Therefore, putting F = C in F = \(\frac {9}{5}\)C + 32, we get
F = \(\frac {9}{5}\)F + 32
⇒ F – \(\frac {9}{5}\)F = 32
⇒ –\(\frac {4}{5}\)F = 32
⇒ F = -40
Therefore at -40, both Fahrenheit and Celsius are numerically the same.