Jharkhand Board JAC Class 9 Maths Solutions Chapter 6 Lines and Angles Ex 6.2 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.2
Page-103
Question 1.
Fig, find the values of x and y and then show that AB || CD.
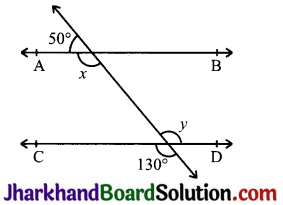
Answer:
x + 50°=180° (Linear pair)
⇒ x = 130°
Also, y = 130° (Vertically opposite angle)
Now, x = y = 130°
Alternate interior angles are equal. Therefore, AB || CD.
Page-104
Question 2.
In Fig, if AB || CD, CD || EF and y : z = 3 : 7, find x.
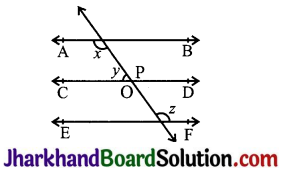
Answer:
Given, AB || CD end CD || EF y : z = 3 : 7
Now, x + y = 180°
(Angles on the same side of transversal.)
also, p = z (Corresponding angles)
and, y + p = 180° (Linear pair)
⇒ y + z = 180°
Let y = 3w and z = 7w
3w + 7w = 180°
⇒ 10 w = 180°
⇒ w = 18°
∴ y = 3×18° = 54° and, z = 7 × 18° = 126°
Now, x + y = 180°
⇒ x + 54° = 180°
⇒ x = 126°
![]()
Question 3.
In Fig, if AB || CD, EF || CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
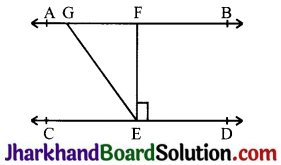
Answer:
Given, AB || CD EF || CD ∠GED = 126°
∠FED = 90° (v EF || CD)
Now, ∠AGE = ∠GED
(Since, AB || CD and GE is transversal.
∴ ∠AGE = 126°
(Alternate interior angles.)
Also, ∠GEF = ∠GED – ∠FED
⇒ ∠GEF = 126° – 90°
⇒ ∠GEF = 36°
Now, ∠FGE + ∠AGE = 180°
⇒ ∠FGE = 180° – 126°
⇒ ∠FGE = 54°
Question 4.
In Fig, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.

[Hint: Draw a line parallel to ST through point R.]
Answer:
Given, PQ 11 ST, ∠PQR =110° and ∠RST = 130°
Construct, a line XY parallel to PQ and ST
∠PQR + ∠QRX= 180°
(Angles on the same side of transversal.)
⇒ 110° + ∠QRX = 180°
⇒ ∠QRX = 70°
Also, ∠RST + ∠SRY = 180°
(Angles on the same side of transversal.)
⇒ 130° + ∠SRY = 180°
⇒ ∠SRY = 50°
Now, ∠QRX + ∠SRY + ∠QRS = 180°
⇒ 70° + 50° + ∠QRS = 180°
⇒ ∠QRS = 60°
Question 5.
In Fig, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
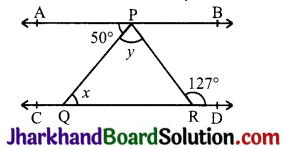
Answer:
Given, AB || CD, ∠APQ = 50° and ∠PRD = 127°
∠PQR = ∠APQ
∴ x = 50° (Alternate interior angles)
∠PRD + ∠RPB = 180°
(Angles on the same side of transversal)
⇒ 127° + ∠RPB = 180°
⇒ ∠RPB = 53°
Now, y + 50° + ∠RPB = 180°
(AB is a straight line.)
⇒ y+50°+ 53°= 180°
⇒ y+ 103° = 180°
⇒ y = 77°
Question 6.
In Fig, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
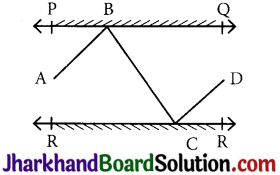
Answer:
Let us draw BE ⊥ PQ and CF ⊥ RS.
As PQ || RS
So, BE || CF
By laws of reflection we know that,
Angle of incidence = Angle of reflection
Thus, ∠1 = ∠2 and ∠3 = ∠4 ……….. (i)
also, ∠2 = ∠3 …………. (ii)
(alternate interior angles because BE || CF and a transversal BC cuts them at B and C)
From (i) and (ii),
∠1 + ∠2 = ∠3 + ∠4
⇒ ∠ABC = ∠DCB
AB || CD
(Alternate interior angles are equal)