Jharkhand Board JAC Class 9 Maths Solutions Chapter 6 Lines and Angles Ex 6.3 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.3
Page-107
Question 1.
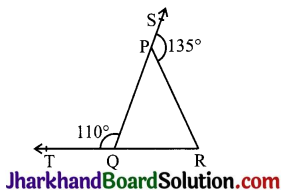
In Fig, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
Answer:
Given, ∠SPR = 135° and ∠PQT = 110°
∠SPR + ∠QPR = 180° (SQ is a straight line)
⇒ 135° + ∠QPR = 180°
⇒ ∠QPR = 45°
Also, ∠PQT +∠PQR = 180° (TR is a straight line)
⇒ 110° + ∠PQR= 180°
⇒ ∠PQR = 70°
Now, ∠PQR + ∠QPR + ∠PRQ = 180°
(Sum of the interior angles of the triangle)
⇒ 70° + 45° + ∠PRQ = 180°
⇒ 115° + ∠PRQ = 180°
⇒ ∠PRQ = 65°
Question 2.
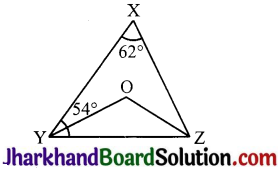
In Fig, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
Answer:
Given ∠X = 62°, ∠XYZ = 54°
YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.
∠X + ∠XYZ + ∠XZY = 180° (Sum of the interior angles of the triangle)
⇒ 62° + 54° + ∠XZY = 180°
⇒ 116° + ∠XZY = 180°
⇒ ∠XZY = 64°
Now, ∠OZY = \(\frac {1}{2}\) ∠XZY (ZO bisector.)
⇒ ∠OZY = 32°
also, ∠OYZ = \(\frac {1}{2}\) ∠XYZ (YO is the bisector.)
⇒ ∠OYZ = 27°
Now, ∠OZY + ∠OYZ + ∠YOZ = 180° (Sum of the interior angles of the triangle)
⇒ 32° + 27° + ∠YOZ = 180°
⇒ 59° + ∠YOZ = 180°
⇒ ∠YOZ = 121°
![]()
Question 3.
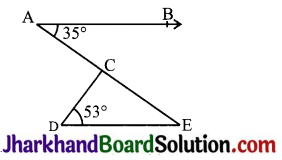
In, Fig , if AB || DE, ∠BAC = 35° and ∠CDE = 53° and ∠DCE.
Answer:
Given, AB || DE, ∠BAC = 35° and ∠CDE = 53°
∠BAC = ∠CED (Alternate interior angles.)
∴ ∠CED = 35°
Now, ∠DCE + ∠CED + ∠CDE = 180° (Sum of the interior angles of the triangle)
⇒ ∠DCE + 35° + 53° = 180°
⇒ ∠DCE + 88° = 180°
⇒ ∠DCE = 92°
Question 4.
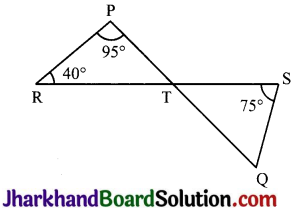
In Fig, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
Answer:
Given, ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°
∠PRT + ∠RPT + ∠PTR = 180° (Sum of the interior angles of the triangle)
⇒ 40° + 95° + ∠PTR = 180°
⇒ 135° + ∠PTR = 180°
⇒ ∠PTR = 45°
∠STQ = ∠PTR = 45° (Vertically opposite angles)
Now, ∠TSQ + ∠STQ + ∠SQT = 180° (Sum of the interior angles of the triangle)
⇒ 75° + 45° + ∠SQT = 180°
⇒ 120° + ∠SQT = 180°
⇒ ∠SQT = 60°
Page-108
Question 5.
In Fig, if PQ || PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
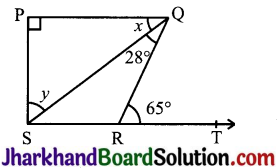
Answer:
Given, PQ || PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°
x + ∠SQR = ∠QRT (Alternate angles as QR is transversal)
⇒ x + 28° = 65°
⇒ x = 37°
also, ∠QSR = x (Alternate angles)
⇒ ∠QSR = 37°
also, ∠QRS+∠QRT=180°(Linear pair)
⇒ ∠QRS + 65° = 180°
⇒ ∠QRS =115°
Now, ∠P + ∠Q+ ∠R + ∠S = 360°
(Sum of the angles in a quadrilateral)
⇒ 90° + 65° + 115° + ∠S = 360°
⇒ 270° + y + ∠QSR = 360°
⇒ 270° + y + 37° = 360°
⇒ 307° + y = 360°
⇒ y = 53°
![]()
Question 6.
In Fig, the side QR of APQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = \(\frac{1}{2}\) ∠QPR.
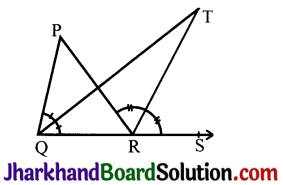
Answer:
Given: Bisectors of ∠PQR and ∠PRS meet at point T.
To prove: ∠QTR = \(\frac{1}{2}\) ∠QPR.
Proof: ∠TRS = ∠TQR + ∠QTR (Exterior angle of a triangle equals the sum of its interior opposite angles.)
⇒ ∠QTR = ∠TRS – ∠TQR …………(i) also,
∠SRP = ∠QPR + ∠PQR
∵ 2 ∠TRS = ∠QPR + 2 ∠TQR
⇒ ∠SRP = 2∠TRS and ∠PQR = 2∠TQR
⇒ ∠QPR = 2 ∠TRS – 2 ∠TQR
⇒ \(\frac{1}{2}\) QPR = ∠TRS – ∠TQR …………(ii)
Equating (i) and (ii)
∠QTR = \(\frac{1}{2}\) ∠QPR
∴ Hence, proved.