Jharkhand Board JAC Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.9 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.9
Question 1.
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see Fig. 13.31). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
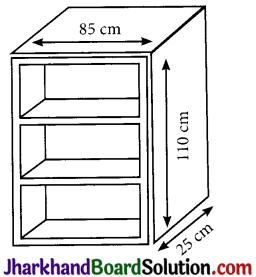
Solution:
Let L, B, H be the external length, breadth and height of the bookshelf
Here L= 110 cm, B= 85 cm, H = 25 cm
let l, b, h be the internal length, breadth and height of the bookshelf
Thickness of the plank = 5cm
l = (110 – 5 – 5) cm = 100cm
b = (85 – 5 – 5) cm = 75cm,
h = (25 – 5) cm = 20 cm
External surface area of the bookshelf = LB + 2 (BH + RL)
= 110 × 85 cm2 + 2(85 × 25 + 25 × 110) cm2
= (9350 ÷ 9750) cm2 = 19100 cm2
Surface area of the border
= (4 × 75 × 5 + 110 × 5 × 2) cm2
= (1500 + 1100) cm2 =2600 cm2
∴ Total surface area to be polished
= (19100 + 2600) cm2
= 21700 cm2
Rate of polishing per cm2 = 20 paise = ₹ \(\frac{20}{100}\)
∴ Cost of polishing the outer surface = ₹ \(\frac{21700 \times 20}{100}\) = ₹ 4340 ……(i)
Area to be painted = lb + 2 (bh + hl)
= 100 × 75 + 2 (75 × 20 + 20 × 100)
= 7500 + 7000
= 14500 cm2
Surface area of two rack = 4 × 75 × 20 = 6000 cm2
Inner Surface area covered by rack = (75 × 5 × 2 + 20 × 5 × 4)
= 1150 cm2
Total Surface area to be painted = 14500 + 6000 – 1150 = 19350 cm2
Cost of painting the inner surface at the rate of 10 paise per cm2
= ₹ \(\frac{19350 \times 10}{100}\) = ₹ 1935
Form (i) and (ii), we have
Total expenses required for polished and painting the surface of the bookshelf.
= ₹ 4340 + ₹ 1935 = ₹ 6275
![]()
Page-237
Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in Fig. 13.32. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.
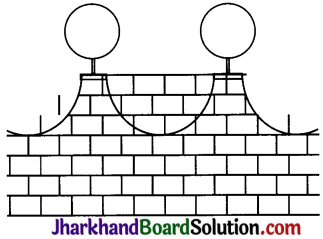
Solution:
Let R be the radius of the sphere and R, H be the radius and height of cylinder.
Radius of sphere (R) = \(\frac{21}{2}\) = 10.5 cm
Surface area of a sphere = 4πr2
= 4 × \(\frac{22}{7}\) × 10.5 × 10.5 cm2
Area of the top of the cylinder (support) = πR2
= π(1.5)2 = cm2
= 7.07 cm2
Area of the sphere to be painted silver = (1386 – 7.07) cm2
= 1378. 93 cm2
Cost of silver paint per cm2 = 25 paise
Cost of painting spheres = ₹ \(\frac{8 \times 1387.93 \times 25}{100}\)
= ₹ 2757.86 (approx.)
Curved surface area of a cylinder (support) = 2πRH
= 2 × \(\frac{22}{7}\) × 1.5 × 7 cm2
Cost of black paint per cm2 = 5 paise
Curved surface area of 8 supports = 8 × 2 × \(\frac{22}{7}\) × 1.5 × 7 cm2
Cost of painting the supports
= ₹ 8 × 2 × \(\frac{22}{7}\) × 1.5 × 7 × \(\frac{5}{100}\)
= ₹ 26.40
Total cost = ₹ (2757.86 + 26.40)
= ₹ 2784.26.
![]()
Question 3.
The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution:
Let the diameter of sphere be 2r.
Then, Radius of the sphere =r
Surface area of sphere = 4πr2 …..(i)
New diameter of the sphere = 2r – 2r × \(\frac{25}{100}\) = \(\frac{3r}{2}\)
New radius of the sphere = \(\frac{3r}{4}\)
Surface area of the new sphere
= \(=4 \pi\left(\frac{3 r}{4}\right)^2=\frac{9 \pi r^2}{4}\)
Decrease in surface area = 4πr2 – \(\frac{9 \pi r^2}{4}\) = \(\frac{7 \pi r^2}{4}\)
Percent decrease
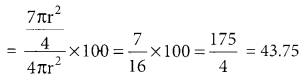
Hence, the surface area decrease by 43.75%.