Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2
Page-159
Question 1.
In Fig, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
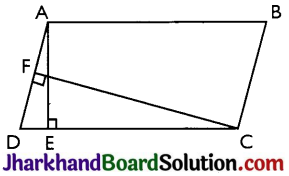
Answer:
Given: AB = CD = 16 cm (Opposite sides of a parallelogram)
CF = 10 cm and AE = 8 cm
Now, Area of parallelogram = Base × Altitude = CD × AE = AD × CF
⇒ 16 × 8 = AD × 10
⇒ AD = \(\frac{128}{10}\) cm
⇒ AD = 12.8 cm
![]()
Question 2.
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that
ar(EFGH) = \(\frac{1}{2}\) ar(ABCD)
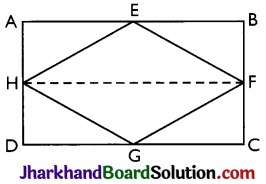
Answer:
Given: E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD.
To Prove: ar (EFGH) = \(\frac{1}{2}\) ar(ABCD)
Construction: H and F are joined.
Proof: AD || BC and AD = BC (Opposite sides of a Parallelogram)
⇒ AH || BF and \(\frac{1}{2}\) AD = \(\frac{1}{2}\) BC
⇒ AH || BF and AH = BF (Hand Fare mid points)
Thus, ABFH is a parallelogram.
[Since a pair of lines is equal and parallel]
⇒ AB || HF
Now, AEFH and ||gm ABFH lie on the same base FH and between the same parallel lines AB and HF.
∴ area of AEFH = \(\frac{1}{2}\) area of ABFH ……..(i)
AD || BC and AD = BC [Opposite sides of a parallelogram ABCD]
⇒ DH CF and \(\frac{1}{2}\) AD = \(\frac{1}{2}\) BC
⇒ DH || CFand DH = CF [As Hand Fare mid-point of AD and BC respectively]
⇒ CDHF is a parallelogram [Since a pair of opposite sides is equal and parallel]
Now, AFGH and parallelogram CDHF lie an same base HF and between the same parallel lines HF and CD
∴ area of AFGH = \(\frac{1}{2}\) area of CDHF ……..(ii)
Adding (i) and (ii),
area of AEFH + area of AGHF
= \(\frac{1}{2}\) area of ABFH + \(\frac{1}{2}\) area of HFCD
⇒ area of EFGH = \(\frac{1}{2}\) area of ABCD
⇒ ar (EFGH) = \(\frac{1}{2}\) ar(ABCD)
Question 3.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB) = ar(BQC).
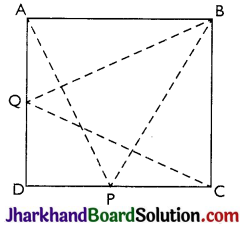
Answer:
∆APB and ||gm ABCD are on the same base AB and between same parallels AB and DC.
Therefore, (∆APB) = ar(||gm ABCD) ……….(i)
Similarly,
ar(∆BQC) = \(\frac{1}{2}\) ar(||gm ∆BCD) ………(ii)
From (i) and (ii),
we have, ar(∆APB) = ar(∆BQC)
Question 4.
In Fig, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(∆APB) + ar(∆PCD) = \(\frac{1}{2}\) ar(||gm ABCD)
(ii) ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)
[Hint: Through P, draw a line parallel to AB.]
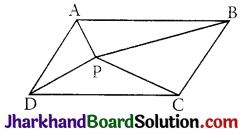
Answer:
Img 5
(i) Draw a line GH is drawn parallel to AB passing through P.
In parallelogram ABCD
AB || GH (by construction) …………(i)
AD || BC (Opposite sides of parallelogram ABCD)
⇒ AG || BH …(ii)
From equations (i) and (ii),
ABHG is a parallelogram.
Now, ∆APB and parallelogram ABHG are lying on the same base AB and between the same parallel lines AB and GH.
∴ ar(∆APB) = \(\frac{1}{2}\) ar(∆BHG) …(iii)
Now, AB || GH (By construction)
AB || CD (Opposite sides of parallelogram)
⇒ CD || GH (Lines parallel to same line are parallel to each other)
Also, CH || GD (as AD || BC)
∴ CDGH is a parallelogram.
Now, APCD and parallelogram CDGH are lying on the same base CD and between the same parallel lines CD and GH.
ar(APCD) = \(\frac{1}{2}\) ar(CDGH)
Adding equations (iii) and (iv),
ar(AAPB) + ar(APCD) = \(\frac{1}{2}\) [ar(ABHG) + ar(CDGH)]
⇒ ar(AAPB) + ar(APCD) = \(\frac{1}{2}\) ar(||gm ABCD).
(ii) A line EF is drawn parallel to AD passing through P.
In a parallelogram ABCD
AD || EF (by construction) ……..(v)
Also, AB || CD
⇒ AE || DF ………..(vi)
From equations (v) and (vi), AEFD is a parallelogram.
Now, ∆ APD and parallelogram AEFD are lying on the same base AD and between the same parallel lines AD and EF.
ar(∆APD) = \(\frac{1}{2}\) ar(AEFD) ……(vii)
Now, AD || EF (By construction) AD||BC (Opposite sides of parallelogram)
⇒ BC || EF
Also, AB || CD
⇒ BE || CF
BCFE is a parallelogram.
Also, ∆PBC and parallelogram BCFE are lying on the same base BC and between the same parallel lines BC and EF.
∴ ar(∆PBC) = \(\frac{1}{2}\) ar(BCFE) …(viii)
Adding equations (vii) and (viii),
ar(∆APD) + ar(∆PBC)
= \(\frac{1}{2}\) [ar(AEFD) + ar(BCFE)]
= \(\frac{1}{2}\) ar(ABCD)
⇒ ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)
Question 5.
In Fig, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(∆AXS) = \(\frac{1}{2}\) ar(PQRS)
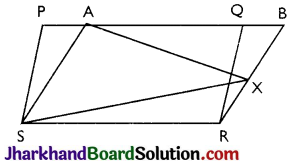
Answer:
(i) Parallelogram PQRS and ABRS lie on the same base SR and between the same parallel lines SR and PB.
∴ ar(PQRS) = ar(ABRS) …………(i)
(ii) ∆AXS and parallelogram ABRS are lying on the same base AS and between the same parallel lines AS and BR.
ar(∆AXS) = \(\frac{1}{2}\) ar(ABRS) …(ii)
From (i) and (ii),
ar(∆AXS) = \(\frac{1}{2}\) ar(PQRS)
Page-160
Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In howT many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow7 wheat and pulses in equal portions of the field separately. How should she do it?
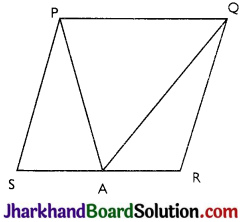
Answer:
The field is divided into three parts. The three parts are in the shape of triangles.
These are ∆PSA, ∆PAQ and ∆QAR.
Area of ∆PSA + ∆PAQ + ∆QAR = Area of PQRS …….(i)
Area of APAQ = \(\frac{1}{2}\) area of PQRS ……….(ii)
(v Triangle and parallelogram are on the same base and between the same parallel lines.)
From (i) and (ii),
Area of ∆PSA + Area of ∆QAR = \(\frac{1}{2}\) area of PQRS … (iii)
Clearly from (ii) and (iii),
Farmer must sow wheat or pulses in ∆PAQ or in both ∆PSA and ∆QAR.