Jharkhand Board JAC Class 9 Maths Solutions Chapter 6 Lines and Angles Ex 6.1 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 6 Lines and Angles Ex 6.1
Page-96
Question 1.
In Fig, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
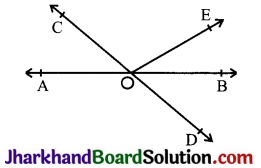
Answer:
Given,
∠AOC + ∠BOE = 70° and ∠BOD = 40°
∠AOC + ∠BOE + ∠COE = 180° (Forms a straight line)
⇒ 70° + ∠COE = 180°
⇒ ∠COE = 110°
∴ Reflex ∠COE = 360° – ∠COE = 360°- 110° = 250°
Also, ∠COE + ∠BOD + ∠BOE = 180° (Forms a straight line)
⇒ 110° + 40° + ∠BOE = 180°
⇒ 150° + ∠BOE = 180°
⇒ ∠BOE = 30°
Page-97
Question 2.
In Fig, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
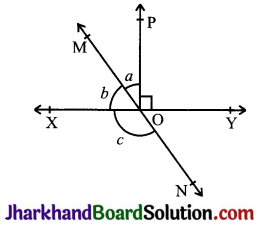
Answer:
Given, ∠POY = 90° and a : b = 2 : 3
∠POY + a + b = 180°
⇒ 90° + a + b = 180°
⇒ a + b = 90°
Let a be 2x and b be 3x.
∴ 2x + 3x = 90°
⇒ 5x = 90°
⇒ x = 18°
∴ a = 2 × 18° = 36° and b = 3 × 18° = 54°
Also, b + c = 180° (Linear Pair)
⇒ 54° + c = 180°
⇒ c = 126°
![]()
Question 3.
In Fig, if ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
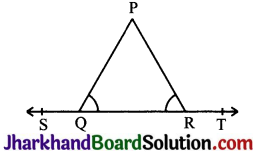
Answer:
Given: ∠PQR = ∠PRQ
To prove: ∠PQS = ∠PRT
Proof: ∠PQR + ∠PQS = 180° (Linear Pair)
⇒ ∠PQS = 180° – ∠PQR …….(i)
also, ∠PRQ + ∠PRT = 180° (Linear Pair)
⇒ ∠PRT = 180°- ∠PRQ
∠PRT = 180° – ∠PQR (∠PQR = ∠PRQ)…(ii)
From (i) and (ii)
∠PQS = ∠PRT = 180° – ∠PQR
Therefore, ∠PQS = ∠PRT
Question 4.
In Fig, if x + y = w + z, then prove that AB is a line.
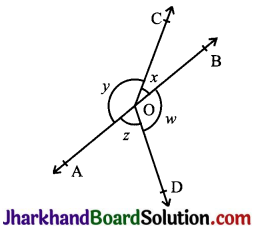
Answer:
Given: x + y = w + z
To prove: AB is a line or x + y = 180° (linear pair)
Proof: x + y + w + z = 360° (Angles around a point)
⇒ (x + y) + (x + y) = 360° (Given x + y = w + z)
⇒ 2(x + y) = 360°
⇒ (x + y) = 180°
Hence, x + y makes a linear pair. Therefore, AB is a straight line.
Question 5.
In Fig, if PQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR.
Prove that ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
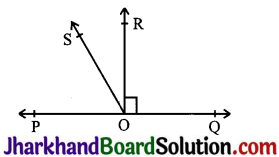
Answer:
Given: OR is perpendicular to line PQ
To prove: ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS).
Proof: ∠POR = ∠ROQ = 90° (Perpendicular)
∠QOS=∠ROQ+∠ROS=90°+∠ROS ……(i)
∠POS = ∠POR – ∠ROS = 90° – ∠ROS …….(ii)
Subtracting (ii) from (i)
∠QOS – ∠POS = (90° + ∠ROS) – (90° – ∠ROS)
⇒ ∠QOS – ∠POS = 90° + ∠ROS – 90° + ∠ROS
⇒ ∠QOS – ∠POS = 2 ∠ROS
⇒ ∠ROS = \(\frac{1}{2}\) (∠QOS – ∠POS)
Hence, proved.
![]()
Question 6.
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
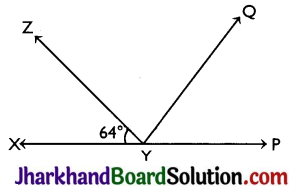
Answer:
Given ∠XYZ = 64°
YQ bisects ∠YP
∠XYZ + ∠ZYP = 180° (Linear Pair)
⇒ 64° + ∠ZYP = 180°
⇒ ∠ZYP = 116°
Also, ∠ZYP = ∠ZYQ + ∠QYP
∠ZYQ = ∠QYP (YQ bisects ZYP)
⇒ ∠ZYP = 2 ∠ZYQ
⇒ 2 ∠ZYQ =116°
⇒ ∠ZYQ = 58° = ∠QYP
Now, ∠XYQ = ∠XYZ + ∠ZYQ
⇒ ∠XYQ = 64° + 58°
⇒ ∠XYQ = 122°
Also, reflex ∠QYP = 180° + ∠XYQ
= 180° + 122° = 302°