JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4

by

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2.4

Question 1.
Determine which of the following polynomials has (x + 1) a factor:
(i) x3 + x2 + x + 1
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
(iv) x3 – x2 – (2 + \( \sqrt{2} \))x + \( \sqrt{2} \)
Answer:
(i) If (x + 1) is a factor of p(x)
=x3 + x2 + x + 1, p(-1) must be zero.
p(-1) = (-1)3 + (-1)2 + (-1) + 1
= – 1 + 1 – 1 + 1 = 0
Therefore, x + 1 is a factor of this polynomial.

(ii) If (x+ 1) is a factor of p(x)
= x4 + x3 + x2 + x + 1, p(-1) must be zero.
∴ p(-1) = (-1)4 + (-1)3 + (-1)2 + (-1) + 1
= 1 – 1 + 1 – 1 + 1 = 1 ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

(iii) If (x + 1) is a factor of polynomial
x4 + 3x3 + 3x2 + x + 1, p(-1) must be 0.
P(-1) = (-1)4 + 3(-1)3 + 3(-1)2 + (-1) + 1
= 1 – 3 + 3 – 1 + 1 = 1 ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

(iv) If (x + 1) is a factor of polynomial
p(x) = x3 – x2 – (2 + \( \sqrt{2} \))x + \( \sqrt{2} \) , p(-1) must be 0.
p(-1) = (-1)3 – (-1)2 – (2 + \( \sqrt{2} \))(-1) + \( \sqrt{2} \)
= -1 – 1 + 2 + \( \sqrt{2} \) + \( \sqrt{2} \)
= 2\( \sqrt{2} \) ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4

Question 2.
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
(iii) p(x) = x3 – 4x2 + x + 6, g(x) = x – 3
Answer:
(i) If g(x) = x + 1 is a factor of given polynomial p(x), then p(- 1) must be zero.
P(-1) = 2(-1)3 + (-1)2 – 2(-1) – 1
= 2(-1) + 1 + 2 – 1 = 0
Hence, g(x) = x + 1 is a factor of p(x).

(ii) If g(x) = x + 2 is a factor of given polynomial p(x),then p(-2) must be 0.
p(-2) = (-2)3 + 3(-2)2 + 3(-2) + 1
= – 8 + 12 – 6 + 1 = -1 ≠ 0
Hence g(x) = x + 2 is not a factor of p(x).

(iii) If g(x) = x – 3 is a factor of given polynomial p(x), then p(3) must be 0.
p(3) = (3)3 – 4(3)2 + 3 + 6 = 27 – 36 + 9 = 0

Therefore, g(x) = x – 3 is a factor of p(x).

Page – 44

Question 3.
Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2 + x + k
(ii) p(x) = 2x2 + kx + \( \sqrt{2} \)
(iii) p(x) = kx2 – \( \sqrt{2} \) x + 1
(iv) p(x) = kx2 – 3x + k
Answer:
(i) If x – 1 is a factor of polynomial p(x)
= x2 + x + k, then p(1) = 0
⇒ (1)2+ 1 + k = 0
⇒ 2 + k = 0
⇒ k = – 2
Therefore, value of k is – 2.

(ii) If x – 1 is a factor of polynomial p(x) = 2x2 + kx + \( \sqrt{2} \) , then p(1) = 0
⇒ 2(1)2 + k(1) + = 0
⇒ 2 + k + \( \sqrt{2} \) = 0
⇒ k = – 2 – \( \sqrt{2} \) = – (2 + \( \sqrt{2} \))
Therefore, value of k is – (2 + \( \sqrt{2} \) ).

(iii) If x – 1 is a factor of polynomial p(x) = kx2 – \( \sqrt{2} \) x + 1, then p(1) = 0
⇒ k(1)2 – \( \sqrt{2} \) (1) + 1 = 0
⇒ k – \( \sqrt{2} \) +1 = 0
⇒ k = \( \sqrt{2} \) – 1
Therefore, value of k is \( \sqrt{2} \) – 1.

(iv) If x – 1 is a factor of polynomial p(x) = kx2 – 3x + k, then p(1) = 0
⇒ k(1)2 – 3(1) + k = 0
⇒ k – 3 + k= 0
⇒ 2k – 3 = 0
Therefore, value of k is \(\frac{3}{2}\)

Question 4.
Factorise:
(i) 12x2 – 7x + 1
(ii) 2x2 + 7x + 3
(iii) 6x2 + 5x – 6
(iv) 3x2 – x – 4
Answer:
(i) 12x2 – 7x + 1
= 12x2 – 4x – 3x+ 1
= 4x (3x – 1) – 1 (3x – 1)
= (3x – 1) (4x – 1)

(ii) 2x2 + 7x + 3
= 2x2 + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x + 1)

(iii) 6x2 + 5x – 6
= 6x2 + 9x – 4x – 6
= 3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)

JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4

(iv) 3x2 – x – 4
= 3x2 – 4x + 3x – 4
= x (3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)

Question 5.
Factorise:
(i) x3 – 2x2 – x + 2
(ii) x3 – 3x2 – 9x – 5
(iii) x3 + 13x2 + 32x + 20
(iv) 2y3 + y2 – 2y – 1
Answer:
(i) Let p(x) = x3 – 2x2 – x + 2
Factors of 2 are ±1 and ± 2
By trial method, we find that p(-1) = 0
So, (x + 1) is factor of p(x)
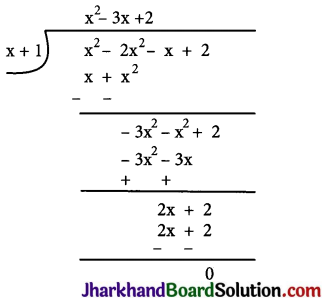
JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 - 1
Now, Dividend = Divisor × Quotient + Remainder
= (x + 1) (x2 – 3x + 2)
= (x + 1) (x2 – x – 2x + 2)
= (x+ 1) {x(x – 1) – 2(x – 1)}
= (x + 1) (x – 1) (x – 2)

(ii) Let p(x) = x3 – 3x2 – 9x – 5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x – 5) is factor of p(x)
JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 - 2
Now, Dividend = Divisor × Quotient + Remainder
= (x – 5) (x2 + 2x + 1)
= (x – 5) (x2 + x + x + 1)
= (x – 5) {x(x + 1) +l(x + 1)}
= (x – 5) (x + 1) (x + 1)

(iii) Let p(x) = x3 + 13x2 + 32x + 20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
P(-1) = 0
So, (x+1) is factor ofp(x)
JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 - 3
Now, Dividend = Divisor × Quotient + Remainder
= (x + 1) (x2 + 12x + 20)
= (x + 1) (x2 + 2x + 10x + 20)
= (x + 1) {x(x+2) +10(x+2)}
= (x + 1) (x+2) (x+10)

JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4

(iv) Let p(y) = 2y3 + y2 – 2y – 1
Factors of ab = 2 × (-1) = – 2 are ±1 and ±2
By trial method, we find that p(1) = 0
So, (y – 1) is factor of p(y)
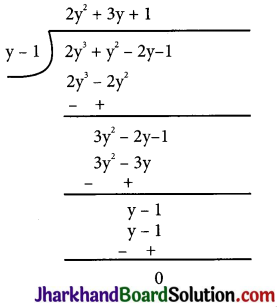
JAC Class 9 Maths Solutions Chapter 2 Polynomials Ex 2.4 - 4
Now, Dividend = Divisor × Quotient + Remainder
= (y – 1) (2y2 + 3y + 1)
= (y – 1) (2y2 + 2y + y + 1)
= (y – 1) {2y(y + 1) + 1(y + 1)}
= (y – 1 )(2y + 1) (y + 1)

Leave a Comment