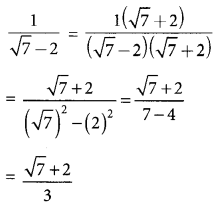JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.5

Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.5 Textbook Exercise Questions and Answers.

JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.5

Question 1.
Classify the following numbers as rational or irrational:
(i) 2 – \(\sqrt{5}\)
(ii) (3 + \( \sqrt{23}\)) – \(\sqrt{23}\)
(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
(iv) \(\frac{1}{\sqrt{2}}\)
(v) 2π
Answer:
(i) 2 – \(\sqrt{5}\) = 2 – 2.2360679…
= -0.2360679…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

(ii) (3 + \(\sqrt{23}\)) – \(\sqrt{23}\)
3 + \( \sqrt{23}\) – \(\sqrt{23}\)
= 3 = \(\frac{3}{1}\)
The number is rational number as it can represented in \(\frac{p}{q}\) form, where p, q ∈ Z, q ≠ 0

(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
The number is rational number as it can represented in \(\frac{p}{q}\) form, where p, q ∈ Z, q ≠ 0

(iv) \(\frac{1}{\sqrt{2}}\)
= 0.7071067811…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

(v) 2π = 2 × 3.1415… = 6.2830…
Since the number is non-terminating non-recurring therefore, it is an irrational number.

Question 2.
Simplify each of the following expressions:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))²
(iv) (\(\sqrt{5}\) – \(\sqrt{2}\))(\(\sqrt{5}\) + \(\sqrt{2}\))
Answer:
(i) (3 + \(\sqrt{3}\)) (2 + \(\sqrt{2}\))
= 3 × 2 + 2\(\sqrt{3}\) + 3\(\sqrt{2}\) + \(\sqrt{3}\) ×\(\sqrt{2}\)
= 6 + 2\(\sqrt{3}\) + 3\(\sqrt{2}\) + \(\sqrt{6}\)

(ii) (3 + \(\sqrt{3}\)) (3 – \(\sqrt{3}\))
= 3²– (\(\sqrt{3}\))² = 9 – 3 = 6
[∵ (a + b) (a – b) = a² – b²]

(iii) (\(\sqrt{5}\) + \(\sqrt{2}\))²
= (\(\sqrt{5}\))² + (\(\sqrt{2}\))² + 2 × \(\sqrt{5}\) × \(\sqrt{2}\)
[∵ (a + b)² = a² + b² + 2ab]
= 5 + 2 + 2 × \(\sqrt{5}\) ×\(\sqrt{2}\)
= 7 + 2\(\sqrt{10}\)

(iv) (\(\sqrt{5}\) – \(\sqrt{2}\))(\(\sqrt{5}\) + \(\sqrt{2}\))
= (\(\sqrt{5}\))² – (\(\sqrt{2}\))²
= 5 – 2 = 3
[∵ (a + b) (a – b) = a² – b²]

Question 3.
Recall, 7t is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, n = c/d. This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Answer:
There is no contradiction. When we measure a value with a scale, we only obtain an approximate value. We never obtain an exact value. Therefore, we may not realise that either c or d is irrational. The value of n is almost equal to 22/7 or 3.14159…

Question 4.
Represent \(\sqrt{9.3}\) on the number line.
Answer:
Step 1: Draw a line segment AB of 9.3 units. Extend it to C so that BC is of 1 unit.
Step 2: Now, AC = 10.3 units. Find the midpoint of AC and name it as O.
Step 3: Draw a semicircle with radius OC and centre O.
Step 4: Draw a perpendicular line segment BD to AC at point B which intersects the semicircle at D. Also, Join OD.
Step 5: Now, OBD is a right angled triangle.

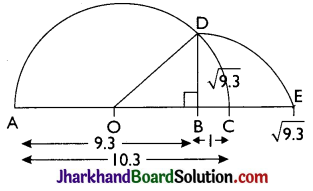
Here, OD = 10.3/2 (radius of semicircle),
OC = \(\frac{10.3}{2}\), BC = 1
OB = OC – BC = (\(\frac{10.3}{2}\)) – 1 = \(\frac{8.3}{2}\)
Using Pythagoras theorem
OD² = BD² + OB²

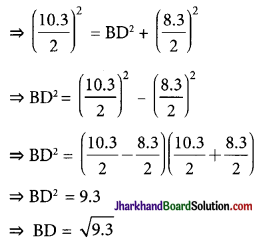
Thus, the length of BD is \(\sqrt{9.3}\) units.

Step 6: Taking BD as radius and B as centre draw an arc which touches the line segment AC extended at the point E. The point E is at a distance of \(\sqrt{9.3}\) from B as shown in the figure.

Question 5.
Rationalise the denominators of the following:
(i) \(\frac{1}{\sqrt{7}}\)
(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
(iv) \(\frac{1}{\sqrt{7}-2}\)
Answer:
(i) \(\frac{1}{\sqrt{7}}\) = \(\frac{1 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}\) = \(\frac{\sqrt{7}}{7}\)

(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)

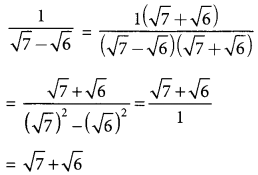
(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)

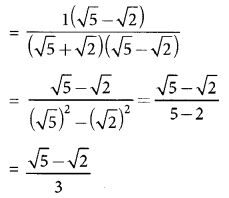
(iv) \(\frac{1}{\sqrt{7}-2}\)