Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 Number Systems Ex 1.2 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 1 Number Systems Exercise 1.2
Question 1.
State whether the following statements are true or false. Justify your Answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form \(\sqrt{m}\) , where m is a natural number.
(iii) Every real number is an irrational number.
Answer:
(i) True, since the collection of real numbers is made up of rational and irrational numbers.
(ii) False, since negative numbers cannot be expressed as square roots.
(iii) False, as real numbers include both rational and irrational numbers. Therefore, every real number cannot be an irrational number, e.g. 2 is a real number but not an irrational number.
Question 2.
Are the square roots of all positive inte-gers irrational? If not, give an example of the square root of a number that is a rational number.
Answer:
No, the square roots of all positive integers are not irrational. For example \(\sqrt{4}\) = 2, which is rational number.
![]()
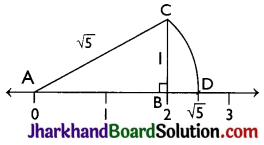
Question 3.
Show how \(\sqrt{5}\) can be represented on the number line.
Answer:
Step 1: Let AB be a line segment of length 2 units on number line.
Step 2: At B, draw a perpendicular line BC of length 1 unit. Join CA.
Step 3: Now, ABC is a right angled triangle. Applying Pythagoras theorem,
AB2 + BC2 = CA2
⇒ 22 + 12 = CA2
⇒ CA2 = 5
⇒ CA = \(\sqrt{5}\)
Thus, CA is a line of length \(\sqrt{5}\) units.
Step 4: Taking CA as a radius and A as a centre draw an arc touching the number line. The point D at which number line gets intersected by arc of length AC is at \(\sqrt{5}\) distance from 0.
Thus, \(\sqrt{5}\) is represented on the number line as shown in the figure.