JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 11 Constructions Ex 11.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 11 Constructions Exercise 11.2

In each of the following, give also the justification of the construction:

Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution :

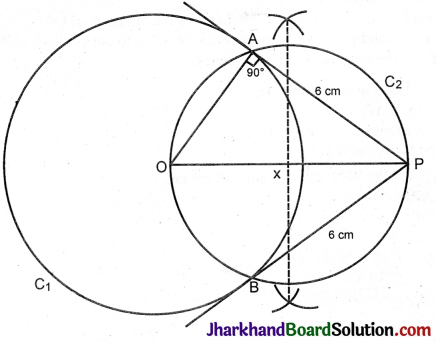
Steps of construction:
1. Draw a line segment OP = 10 cm.
2. With O as centre and 6 cm as radius draw a circle C₁.
3. Draw the perpendicular bisector of OP. Let x be the midpoint of OP.
4. With x as centre and xO or XP as radius draw circle C₂ to cut circle C₁ at A and B.
5. Join PA and PB.
PA and PB are the tangents to the circle from P.
P\(\hat{A}\)O = 90° (Angle in a semicircle)
∴ PA ⊥ radius OA.
∴ PA is a tangent to the circle.

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution :

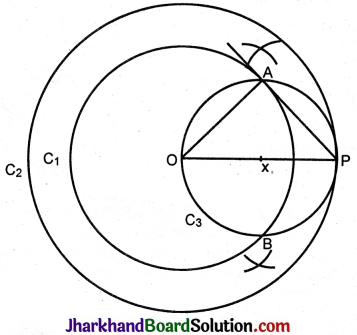
Steps of construction:
1. With O as centre and 4 cm as radius draw circle C₁.
2. With O as centre and 6 cm as radius draw circle C₂.
3. Take a point P on circle C₂.
4. Draw the perpendicular bisector of OP. Let x be the midpoint of OP.
5. With x as centre and xO or xP as radius draw circle C₃ to cut circle C₁ at A and B.
Join PA. PA is the tangent to circle C₁ from P.
O\(\hat{A}\)P = 90° (Angle in the semicircle)
∴ Radius OA ⊥ AP.
Hence PA is a tangent ∴ PA = 4.5 cm.
Verification by calculation:
In ΔOAP, O\(\hat{A}\)P = 90°. OA = 4 cm, OP = 6 cm.
OA² + AP² = OP²
4² + AP² = 6²
AP² = 6² – 4²
= (6 + 4) (6 – 4)
= 10 × 2 = 20
AP = \(\sqrt{20}\)
= \(\sqrt{4 \times 5}\) = 2\(\sqrt{5}\)
= 2 × 2.3 = 4.6 cm.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution :

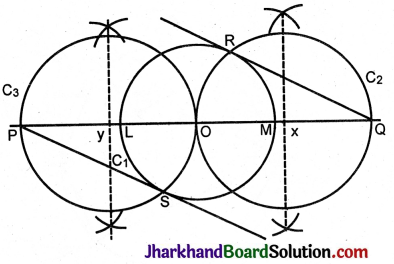
Steps of construction:
1. Draw circle C₁ with centre O and radius = 3 cm.
2. Take a diameter LM in the circle.
3. Take a point P to the left of O at a distance of 7 cm.
4. Take a point Q to the right of O at a distance of 7 cm.
5. From P draw a tangent PS to C₁.
6. From Q draw a tangent RQ to C₂.
PS and RQ are tangents drawn to the circle from points P and Q respectively.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution :

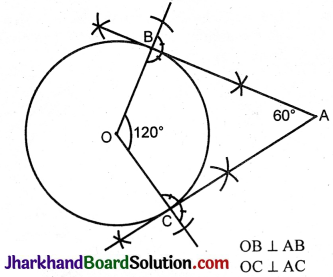
B\(\hat{A}\)O = 60°
∴ B\(\hat{A}\)C = 180° – 60° = 120°
Steps of construction:
1. Draw a circle of radius 5 cm with centre O.
2. At O make an angle BC = 120°.
3. At B and C draw perpendiculars to the radii OB and OC.
4. Let the perpendiculars meet at A.
AB and AC are tangents drawn to the circle from A such that the angle between them is 60°.

Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution :
AC and AD are tangents, drawn from centre A to C₂.
BE and BF are tangents drawn from centre B to C₁.
AC = AD = 7.2 cm, BE = BF = 6.8 cm.
Steps of construction:
1. Draw a line segment AB – 8 cm.
2. With A as centre and radius 4 cm draw circle C₁.
3. With B as centre and radius 3 cm draw circle C₂.

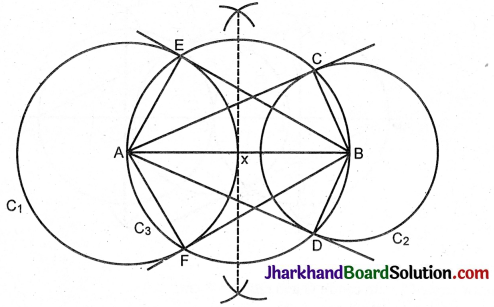
4. Draw the perpendicular bisector of AB. Let x be the midpoint of AB.
5. With x as centre and radius xA or xB draw circle C₃.
6. Let it cut C, at E and F and cut C₂ at C and D.
7. Join AC, AD, BE, BF.
AC and AD are tangents drawn from A, the centre of circle C₁ to circle C₂.
BE and BF are tangents drawn from B, the centre of circle C₂ to circle C₁.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution :

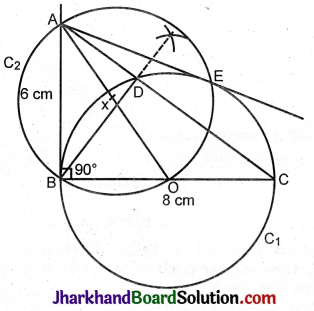
Steps of construction:
1. Construct ΔABC given AB = 6 cm, BC = 8 cm, A\(\hat{B}\)C = 90°.
2. From B draw perpendicular BD to AC.
3. Let O be the midpoint of BC.
4. With O as centre and OB or OC as radius, draw C₁ to pass through B, D and C.
5. Join AO.
6. Draw its perpendicular bisector. Let x be the midpoint of AO.
7. With x as centre and xA or xO as radius, draw circle C₂. Let it cut C₁ at E and B.
8. Join AE. AB is already joined.
AB and AE are tangents to circle C₁ from A.
AE = AB = 6 cm.

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution :

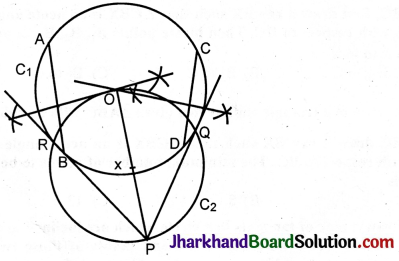
A circle is drawn keeping the bangle on the paper. We have to find its centre.
Draw any two chords AB and CD in it.
Draw their perpendicular bisectors. The point of intersection O of these bisectors gives the centre of the circle.
(The perpendicular bisector of a chord passes through the centre).
Let P be the external point. Join PO. Draw the perpendicular bisector of PO. Let x be the midpoint.
With x as centre and xO or xP as radius draw circle C₂. Let it cut circle C₁ at Q and R.
Join PQ and PR. These are the tangents to the circle C₁.