JAC Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.1

Jharkhand Board JAC Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.1 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 12 Areas Related to Circles Ex 12.1

Unless stated otherwise, use π = \(\frac{22}{7}\)

Question 1.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Solution :
Circumference of circle 1 = 2πr
= 2 × π × 19 cm = 2π × 19
Circumference of circle 2 = 2 × π × 9 cm = 2π × 9
Sum of the circumferences = (2π × 19) + (2π × 9)
= 2π(19 + 9)
= 2π 28
= 56 π.
Circumference of circle 3 = 56π.
2πr = 56π
r = \(\frac{56π}{2π}\)
= 28 cm.

Alternative Method:
r₁ = 19 cm, r₂ = 9 cm, R = ?
2πr₁ + 2πr₂ = 2πR (given)
2π(г₁ + r₂) = 2πR
(19 + 9) = R
∴ R = 28 cm.

Question 2.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Solution :
Area of circle 1 = π × 8² cm²
Area of circle 2 = π × r² = π × 6²
Sum of the areas = π(8² + 6²)
= π(64 + 36)
= 100π
Area of circle 3 = 100 π
πr² = 100 π
r² = \(\frac{100π}{π}\) = 100
∴ r = 10 cm.

Alternative Method:
πr₁² + πr₂² = πR²
π(r₁² + r₂²) = πR²
8² + 6² = R²
64 + 36 = R²
\(\sqrt{100}\) = R
∴ R = 10 cm.

Question 3.
The figure depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Solution :

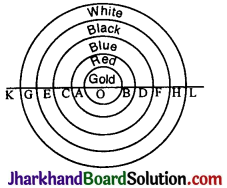
KG = GE = EC = CA = AO = OB = 10.5 cm
Area of the gold band = πr²
= \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}\)
r = \(\frac{AB}{2 }=\frac{21}{2}\) = 10.5
= \(\frac{33 \times 21}{2}=\frac{693}{2}\)
= 346.5 cm².

Area of the red band d = 21 + 10.5 + 10.5 = 42 cm.
= (\(\frac{22}{7} \times \frac{42}{2} \times \frac{42}{2}\)) – 346.5(area of the gold circle)
= (66 × 21) – 346.5
= 1386 – 346.5 = 1039.5 cm².

Area of the blue band d = 6 × 10.5 = 63
= (\(\frac{22}{7} \times \frac{63}{2} \times \frac{63}{2}\)) – area of the red circle
= \(\frac{99 \times 63}{2}\) – (66 × 21)
= \(\frac{6237}{2}\) – 1386
= 3118.5 – 1386.0 = 1732.5 cm²

Area of the black band = d = GH = 8 × 10.5 = 84
= (\(\frac{22}{7} \times \frac{84}{2} \times \frac{84}{2}\)) – area of the blue circle
= \(\frac{22}{7} \times \frac{84}{2} \times \frac{84}{2}\) – (\(\frac{22}{7} \times \frac{63}{2} \times \frac{63}{2}\))
= (132 × 42) – \(\frac{99 \times 63}{2}\)
= 5544.0 – 3118.5 = 2425.5 cm²

Area of the white band = d = KL = 10 × 10.5 = 105
= (\(\frac{22}{7} \times \frac{105}{2} \times \frac{105}{2}\)) – (132 × 42) (area of black circle)
= \(\frac{165 \times 105}{2}\) – (132 × 42)
= \(\frac{17325}{2}\) – 5544
= 8662.5 – 5544.0 = 3118.5 cm².

Question 4.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Solution :
Distance travelled in one revolution = Circumference of the wheel
= 2πr d = 80
= 2 × \(\frac{22}{7} \times \frac{80}{2}=\frac{22 \times 80}{7}\) cm
Distance travelled by the car in 10 min — ?
Speed of the car = 66 km/hr.
Speed of the car = \(\frac{66}{60}\) × 10 = 11 km/min.
= 11 × 1000 mts./min.

Question 5.
Tick the correct answer in the following and justify your choice: If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units.
Solution :
2πr = πr²
2r = r²
Solution :
(A). r = 2 units.