JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

Jharkhand Board JAC Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.2

Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically:
1. 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
2. 5 pencils and 7 pens together cost 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
1. Let the number of boys be x and the number of girls be y.
Then, the equations formed as follows:
x + y = 10 ……. (1)
and y = x + 4,
i.e., y – x = 4 …… (2)
To draw the graphs of these equations,
we find two solutions for each equation.
For equation (1), x + y = 10 gives y = 10 – x.

x	0	5
y	10	5

For equation (2), y – x = 4 gives y = x + 4.

x	0	2
y	4	6

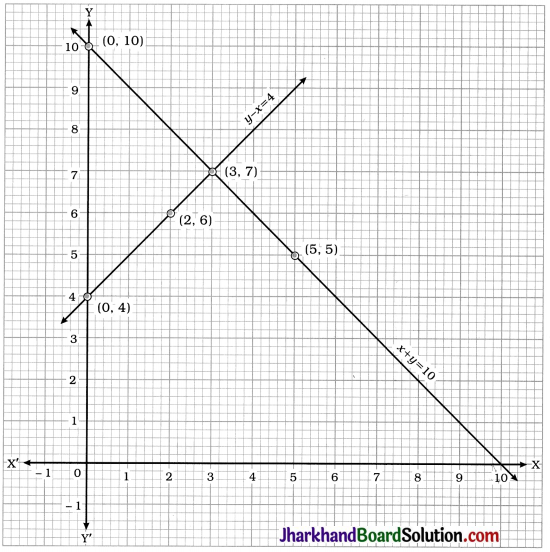
Two lines intersect at point (3, 7). Hence, x = 3 and y = 7 is the required solution of the pair of linear equations.
Thus, 3 boys and 7 girls took part in the quiz.
Verification : x = 3 and y = 7 satisfy both the equations x + y = 10 and y – x = 4.

2. Let the cost of each pencil be ₹ x and the cost of each pen be ₹ y.
Then, from the given information, we receive the following equations:
5x + 7y = 50 ……… (1)
7x + 5y = 46 ……….. (2)
To draw the graphs of these equations, we find two solutions for each equation.
For equation (1), 5x + 7y = 50 gives
y = \(\frac{50-5 x}{7}\)

x	3	10
y	5	0

For equation (2), 7x + 5y = 46 gives
y = \(\frac{46-7 x}{5}\)

x	3	8
y	5	-2

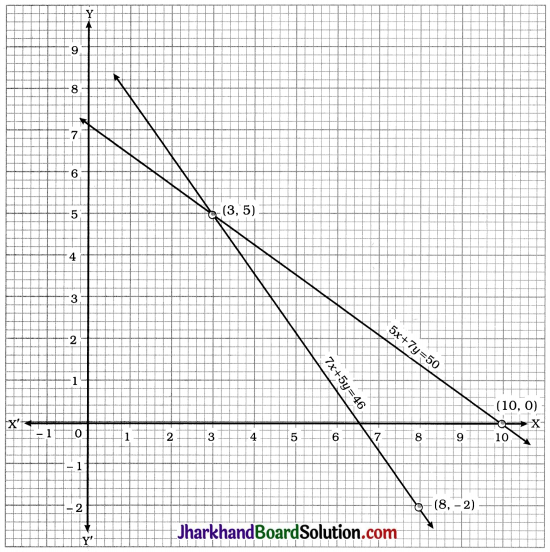
Two lines intersect at point (3, 5). Hence, x = 3 and y = 5 is the required solution of the pair of linear equations.
Thus, the cost of each pencil is ₹ 3 and the cost of each pen is ₹ 5.
Verification : x = 3 and y = 5 satisfy both the equations 5x + 7y = 50 and 7x + 5y = 46.

Question 2.
On comparing the ratios \(\frac{a_1}{a_2}, \frac{b_1}{b_2}\) and \(\frac{c_1}{c_2}\), find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
1. 5x – 4y + 8 = 0; 7x + 6y – 9 = 0
2. 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
3. 6x – 3y + 10 = 0; 2x – y + 9 = 0
Solution:
5x – 4y + 8 = 0; 7x + 6y – 9 = 0
For the given pair of linear equations,
a₁ = 5, b₁ = -4, c₁ = 8, a₂ = 7, b₂ = 6 and c₂ = -9
Now, \(\frac{a_1}{a_2}=\frac{5}{7}, \quad \frac{b_1}{b_2}=\frac{-4}{6}=-\frac{2}{3}\)
and \(\frac{c_1}{c_2}=\frac{8}{-9}=-\frac{8}{9}\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the lines representing the given pair of linear equations intersect at a point.

2. 9x + 3y + 12 = 0; 18x + 6y + 24 = 0
For the given pair of linear equations, a₁ = 9, b₁ = 3, c₁ = 12, a₂ = 18, b₂ = 16 and c₂ = 24.
Now, \(\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the lines representing the given pair of linear equations are coincident lines.

3. 6x – 3y + 10 = 0; 2x – y + 9 = 0
For the given pair of linear equations, a₁ = 6, b₁ = -3, c₁ = 10, a₂ = 2, b₂ = -1 and c₂ = 9.
Now, \(\frac{a_1}{a_2}=\frac{6}{2}=3, \quad \frac{b_1}{b_2}=\frac{-3}{-1}=3\)
and \(\frac{c_1}{c_2}=\frac{10}{9}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the lines representing the given pair of linear equations are parallel lines.

Question 3.
On comparing the ratios \(\frac{a_1}{a_2}, \frac{b_1}{b_2}\) and \(\frac{c_1}{c_2}\), find out whether the following pair of linear equations are consistent or inconsistent:
1. 3x + 2y = 5; 2x – 3y = 7
2. 2x – 3y = 8; 4x – 6y = 9
3. \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
4. 5x – 3y = 11; -10x + 6y = -22
5. \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
Solution:
1. 3x + 2y = 5; 2x – 3y = 7
For the given pair of linear equations, a₁ = 3, b₁ = 2, c₁ = -5, a₂ = 2, b₂ = -3 and c₂ = -7.
Now, \(\frac{a_1}{a_2}=\frac{3}{2}, \frac{b_1}{b_2}=\frac{2}{-3}=-\frac{2}{3}\)
and \(\frac{c_1}{c_2}=\frac{-5}{-7}=\frac{5}{7}\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the given pair of linear equations is consistent.

2. 2x – 3y = 8: 4x – 6y = 9
For the given pair of linear equations,
a₁ = 2, b₁ = -3, c₁ = -8, a₂ = 4, b₂ =-6 and c₂ = -9.
Now, \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{-8}{-9}=\frac{8}{9}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given pair of linear equations is inconsistent.

3. \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
Multiplying the first equation by 6 and expressing both the equations in the standard form, we get following equations:
9x + 10y – 42 = 0; 9x – 10y – 14 = 0
For the given pair of linear equations, a₁ = 9, b₁ = 10, c₁ = -42, a₂ = 9, b₂ = -10 and c₂ = -14.
Now, \(\frac{a_1}{a_2}=\frac{9}{9}=1, \frac{b_1}{b_2}=\frac{10}{-10}=-1\)
and \(\frac{c_1}{c_2}=\frac{-42}{-14}=3\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the given pair of linear equations is consistent.

4. 5x – 3y = 11; -10x + 6y = -22
For the given pair of linear equations, a₁ = 5, b₁ =-3, c₁ = -11, a₂ = -10, b₂ = 6 and c₂ = 22.
Now, \(\frac{a_1}{a_2}=\frac{5}{-10}=-\frac{1}{2}, \frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{-11}{22}=-\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the given pair of linear equations is consistent and dependent.

5. \(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
For the given pair of linear equations, a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = -8, a₂ = 2, b₂ = 3 and c₂ = -12.
Now, \(\frac{a_1}{a_2}=\frac{\frac{4}{3}}{2}=\frac{2}{3}, \quad \frac{b_1}{b_2}=\frac{2}{3}\)
and \(\frac{c_1}{c_2}=\frac{-8}{-12}=\frac{2}{3}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the given pair of linear equations is consistent and dependent.

Question 4.
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
1. x + y = 5; 2x + 2y = 10
2. x – y = 8; 3x – 3y = 16
3. 2x + y – 6 = 0; 4x – 2y – 4 = 0
4. 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
Solution:
1. x + y = 5; 2x + 2y = 10
For the given pair of linear equations,
a₁ = 1, b₁ = 1, c₁ = -5, a₂ = 2, b₂ = 2 and c₂ = -10.
Now, \(\frac{a_1}{a_2}=\frac{1}{2}, \quad \frac{b_1}{b_2}=\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{-5}{-10}=\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Hence, the given pair of linear equations is consistent and dependent.
Now, we draw the graphs of both the equations.
x + y = 5 gives y = 5 – x.

x	0	5
y	5	0

2x + 2y = 10 gives y = \(\frac{10-2 x}{2}\)

x	1	3
y	4	2

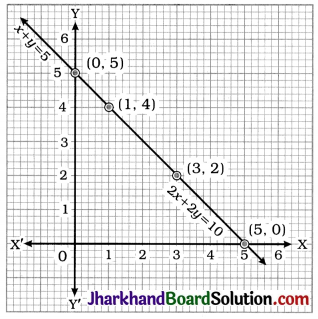
Here, lines representing both the equations. are coincident. Hence, any point on the line gives a solution. In general, y = 5 – x, where x is any real number is a solution of the given pair of linear equations.

2. x – y = 8; 3x – 3y = 16
For the given pair of linear equations, a₁ = 1, b₁ = -1, c₁ = -8, a₂ = 3, b₂ = -3 and c₂ = -16.
Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \quad \frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}\)
and \(\frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given pair of linear equations is inconsistent.

3. 2x + y – 6 = 0; 4x – 2y – 4 = 0
For the given pair of linear equations, a₁ = 2, b₁ = 1, c₁ = -6, a₂ = 4, b₂ = -2 and c₂ = -4.
Now, \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \quad \frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{-6}{-4}=\frac{3}{2}\)
Here, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
Hence, the given pair of linear equations is consistent.
Now, we draw the graphs of both the equations.
2x + y – 6 = 0 gives y = 6 – 2x.

x	0	3
y	6	0

4x – 2y – 4 = 0 gives y = \(\frac{4 x-4}{2}\) = 2x – 2.

x	0	1
y	-2	0

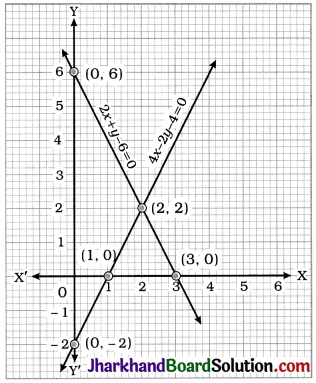
Here, the lines intersect at point (2, 2). Hence, x = 2 and y = 2 is the unique solution of the given pair of linear equations.

4. 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
For the given pair of linear equations, a₁ = 2, b₁ = -2, c₁ = -2, a₂ = 4, b₂ = -4 and c₂ = -5.
Now, \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \quad \frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}\)
and \(\frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}\)
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Hence, the given pair of linear equations is inconsistent.

Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let the length and breadth of the rectangular garden be x m and y m respectively.
Then, from the given data, x = y + 4 and 36 = \(\frac{1}{2}\)[2(x + y)] i.e., x + y = 36 as the perimeter of a rectangle = 2 (length + breadth).
To draw the graphs, we find two solutions of each equation.
x = y + 4 gives y = x – 4

x	8	24
y	4	20

x + y = 36 gives y = 36 – x

x	12	24
y	24	12

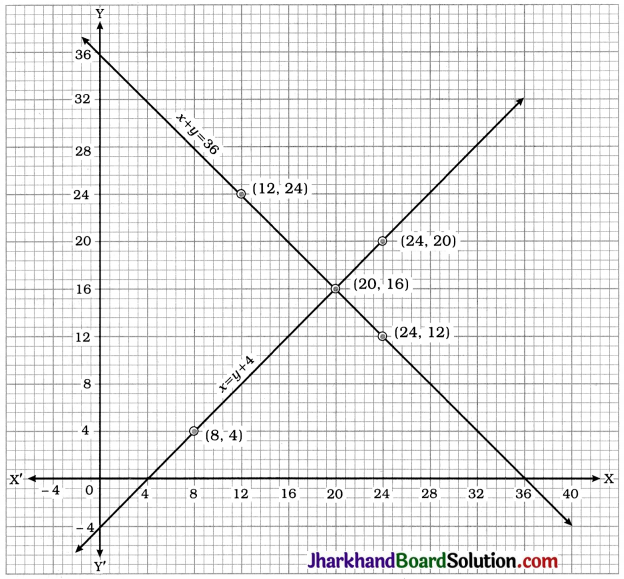
Here, the lines intersect at point (20, 16). Hence, x = 20 and y = 16 is the unique solution of the pair of linear equations.
Thus, for the rectangular garden, length = 20 m and breadth = 16 m.

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
1. intersecting lines
2. parallel lines
3. coincident lines
Solution:
1. For intersecting lines, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\). The given equation is 2x + 3y – 8 = 0. We can give another equation as 3x + 4y – 24 = 0. Here, \(\frac{a_1}{a_2}=\frac{2}{3}\) and \(\frac{b_1}{b_2}=\frac{3}{4}\) satisfying \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

2. For parallel lines, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\). The given equation is 2x + 3y – 8 = 0. We can give another equation as 6x + 9y – 10 = 0.
Here, \(\frac{a_1}{a_2}=\frac{1}{3}, \quad \frac{b_1}{b_2}=\frac{1}{3}\) and \(\frac{c_1}{c_2}=\frac{4}{5}\) satisfying \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\).

3. For coincident lines, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\). The given equation is 2x + 3y – 8 = 0.
We can give another equation as 10x + 15y – 40 = 0. Here, \(\frac{a_1}{a_2}=\frac{1}{5}\), \(\frac{b_1}{b_2}=\frac{1}{5}\) and \(\frac{c_1}{c_2}=\frac{1}{5}\) satisfying \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\).

Question 7.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:
x – y + 1 = 0 gives y = x + 1

x	-1	2
y	0	3

3x + 2y – 12 = 0 gives y = \(\frac{12-3 x}{2}\)

x	0	4
y	6	0

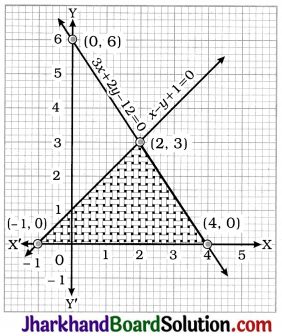
The vertices of the triangle formed by the given lines and the x-axis are (-1, 0), (4, 0) and (2, 3).