JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.3

Jharkhand Board JAC Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.3 Textbook Exercise Questions and Answers.

JAC Board Class 10 Maths Solutions Chapter 2 Polynomials Exercise 2.3

Question 1.
Divide the polynomial p (x) by the polynomial g(x) and find the quotient and remainder in each of the following:
1. p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
2. p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
3. p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
Solution:
1.

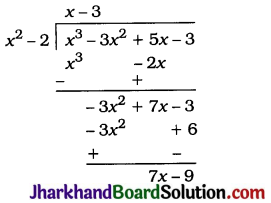
Quotient x – 3, Remainder = 7x – 9

2. p(x) = x⁴ – 3x² + 4x + 5
= x⁴ + 0x³ – 3x² + 4x + 5
and g(x) = x² + 1 – x = x² – x + 1

Quotient = x² + x – 3, Remainder = 8

3. p(x) = x⁴ – 5x + 6
= x⁴ + 0x³ + 0x² – 5x + 6
and g(x) = 2 – x² = -x² + 2

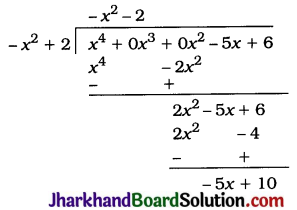
Quotient = -x² – 2, Remainder = – 5x + 10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
1. t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
2. x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
3. x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:
1.

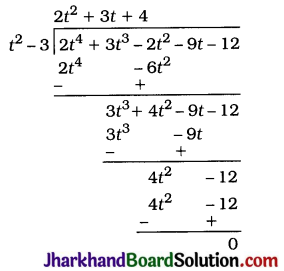
As the remainder is 0, t² – 3 is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

2.

As the remainder is 0, x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

3.

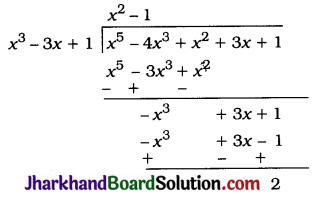
As the remainder is not 0, x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x + 1.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\)
Solution:
Since \(\sqrt{\frac{5}{3}}\) and \(-\sqrt{\frac{5}{3}}\) are given two zeroes of the polynomial, \(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)=x^2-\frac{5}{3}\) is a factor of the given polynomial. Then, to obtain the other zeroes of the polynomial, we divide it by x² – \(\frac{5}{3}\)

Now,
3x² + 6x + 3 = 3(x² + 2x + 1)
= 3(x + 1)²
= 3(x + 1)(x + 1)
Hence, the two zeroes of 3x² + 6x + 3 are 1 and – 1.
Hence, the two zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5 other than the given zeroes are 1 and -1.

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Solution:
Here, dividend p(x) = x³ – 3x² + x + 2, quotient q(x) = (x – 2) and remainder r(x) = (-2x + 4).
Now, p(x) = g(x) × q(x) + r(x)
∴ x³ – 3x² + x + 2 = g(x) × (x – 2) + (-2x + 4)
∴ (x³ – 3x² + x + 2) – (-2x + 4) = g(x) × (x – 2)
∴ x³ – 3x² + 3x – 2 = g(x) × (x – 2)
∴ g(x) = \(\frac{x^3-3 x^2+3 x-2}{x-2}\)

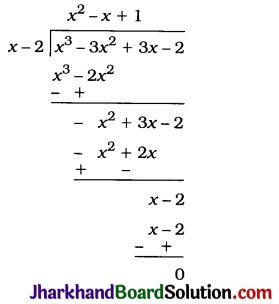
Hence, g(x) = x² – x + 1.

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
1. deg p(x) = deg q(x)
2. deg q(x) = deg r(x)
3. deg r(x) = 0.
Solution:
1. deg p (x) = deg q (x) implies that deg g (x) = 0. i.e., g(x) is a non-zero constant. One such example can be given as p (x) = 3x² + 15x + 13, g(x) = 3, q(x) = x² + 5x + 4 and r(x) = 1, which satisfies the division algorithm as:
3x² + 15x + 13 = 3(x² + 5x + 4) + 1.

2. deg q(x) = deg r (x) implies that deg g (x) > deg q(x), because
deg g (x) > degr (x). One such example can be given as p (x) = x³ + 5x² + 2x + 7, g(x) = x² + 1, q(x) = x + 5 and r(x) = x + 2, which satisfies the division algorithm as:
x³ + 5x² + 2x + 7 = (x² + 1)(x + 5) + (x + 2).

3. deg r(x) = 0 implies that the remainder is a constant. One such example can be given as p (x) = x³ + 4x² + 5x + 9, g(x) = x + 3, q(x) = x² + x + 2 and r(x) = 3, which satisfies the division algorithm as:
x³ + 4x² + 5x + 9 = (x + 3)(x² + x + 2) + 3.
Note: There can be several examples in each of the above cases.