Jharkhand Board JAC Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Ex 8.3 Textbook Exercise Questions and Answers.
JAC Board Class 10 Maths Solutions Chapter 8 Introduction to Trigonometry Exercise 8.3
Question 1.
Evaluate:
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°.
Solution :
\(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) sin θ = cos (90° – θ)
sin 18° = cos (90° – 18°) = cos 72°
∴ \(\frac{sin 18}{cos 72}\) = \(\frac{cos 72°}{cos 72°}\) = 1
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\) tan θ = cot (90 – θ)
tan 26 = cot (90 – 26) = cot 64°.
∴ \(\frac{tan 26°}{cot 64°}\) = \(\frac{cot 64}{cot 64}\) = 1
(iii) cos 48° – sin 42° = cos (90° – 42°) – sin 42°
= sin 42° – sin 42° = 0.
(iv) cosec 31° – sec 59° . cosec θ = sec (90 – θ)
cosec 31 = sec (90 – 31) = sec 59°.
cosec 31° – sec 59° = sec 59° – sec 59° = 0.
![]()
Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1.
(ii) cos 38° cos 52° – sin 38° sin 52° = 0.
Solution :
(i) tan 48° tan 23° tan 42° tan 67° = 1.
LHS = tan 48° tan 23° tan 42° tan 67°
= tan 48° . tan 23° tan (90° – 48°) . tan (90° – 23°)
= tan 48° . tan 23° . cot 48° . cot 23° [∵ tan (90° – θ) = cot θ]
= tan 48° . tan 23° . \(\frac{1}{tan 48°}\) . \(\frac{1}{tan 23°}\) [∵ cot θ = \(\frac{1}{tan θ}\)]
= 1 = RHS.
(ii) cos 38° cos 52° – sin 38° sin 52° = 0.
LHS = cos 38° . cos 52° – sin 38° sin 52°
= cos (90° – 52°) cos (90° – 38°) – sin 38°. sin 52°
= sin 52° . sin 38° – sin 38° . sin 52° [∵ cos (90° – θ) = sin θ]
= 0 = RHS.
Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution :
tan θ = cot (90° – θ)
tan 2A = cot (90° – 2A)
tan 2A = cot (A – 18°) ∵ cot (90° – 2A) = cot (A – 18°)
90° – 2A = A – 18
– 2A – A = – 18 – 90
– 3A = – 108
A = \(\frac{-108}{-3}\) = 36°.
![]()
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution :
tan A = cot B (90° – A)
tan A = cot B
∴ cot (90° – A) = cot B
∴ 90° – A = B
90° = B + A
A + B = 90°.
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution :
sec 4A = cosec (A – 20°)
cosec (90° – 4A) = cosec (A – 20°)
90° – 4A = A – 20°
– 4A – A = – 110°
– 5A = – 110°
A = 22°.
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that
Solution :
sin (\(\frac{B+C}{2}\)) = cos \(\frac{A}{2}\)
sin θ = cos (90° – θ)
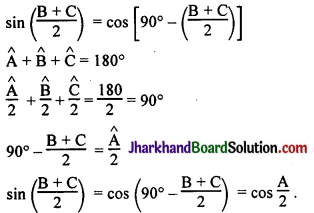
![]()
Question 7.
Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution :
sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°. (Since cos (90° – θ) = sin θ and sin (90° – θ) = cos θ)