Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 Circles Ex 10.5 Textbook Exercise Questions and Answers.
JAC Board Class 9th Maths Solutions Chapter 10 Circles Ex 10.5
Page-184
Question 1.
In the figure, A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
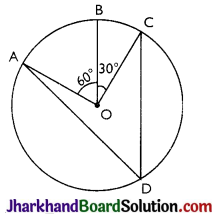
Answer:
Here, ∠AOC = ∠AOB + ∠BOC
∠AOC = 60° + 30°
⇒ ∠AOC = 90°
We know that angle subtended by an arc at centre is double the angle subtended by it at any point on the remaining part of the circle.
∠ADC = \(\frac{1}{2}\) ∠AOC = \(\frac{1}{2}\) × 90° = 45°
Page-185
Question 2.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the nugor arc.
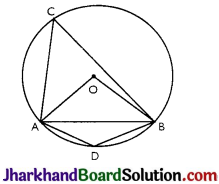
Answer:
Given: Chord AB is equal to the radius of the circle.
In ∆OAB, OA = OB = AB = radius of the circle.
Thus, AOAB is an equilateral triangle.
∠AOB = 60°
also, ∠ACB = \(\frac{1}{2}\) ∠AOB = \(\frac{1}{2}\) × 60° = 30°
ACBD is a cyclic quadrilateral,
∠ACB + ∠ADB = 180° (Opposite angles of cyclic quadrilateral)
⇒ ∠ADB = 180° – 30° = 150°
Thus, angle subtend by the chord at a point on the minor arc and also at a point on the major arc are 150° and 30° respectively.
![]()
Question 3.
In Fig, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
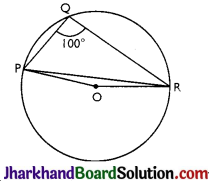
Answer:
Reflex ∠POR = 2 × ∠PQR = 2 × 100° = 200°
∴ ∠POR = 360° – 200° = 160°
In ∆OPR,
OP = OR (radii of the circle)
∠OPR = ∠ORP
(Angles opposite to equal sides)
Now,
∠OPR + ∠ORP +∠POR = 180°
(Sum of the angles in a triangle)
⇒ ∠OPR + ∠OPR + 160° = 180°
⇒ 2∠OPR= 180°- 160°
⇒ ∠OPR =10°
Question 4.
In Fig, ∠ABC = 69°, ∠ ACB = 31°, find ∠BDC.
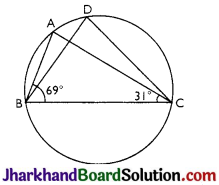
Answer:
∠BAC = ∠BDC (Angles in the same segment of the circle)
In ∆ABC,
∠BAC + ∠ABC+ ∠ACB =180° (Sum of the angles of a triangle)
⇒ ∠BAC + 69°+ 31° = 180°
⇒ ∠BAC = 180°- 100°
⇒ ∠BAC = 80°
Thus, ∠BDC = 80°
Question 5.
In Fig, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠ BAC.
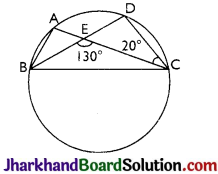
Answer:
∠BAC = ∠CDE
(Angles in the segment of the circle)
In ∆CDE,
∠CEB = ∠CDE + ∠DCE (Exterior angles of the triangle)
=> 130° = ∠CDE + 20°
⇒ ∠CDE =110°
Thus, ∠BAC = 110°
Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
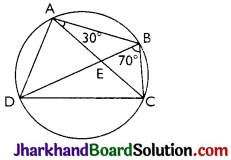
Answer:
For chord CD,
∠CBD = ∠CAD (Angles in same segment)
∴ ∠CAD = 70°
∠BAD = ∠BAC + ∠CAD
= 30° + 70° = 100°
∠BCD + ∠BAD = 180° (Opposite angles of a cyclic quadrilateral)
⇒ ∠BCD + 100° = 180°
⇒ ∠BCD = 80°
In ∆ABC, AB = BC (given)
∠BCA = ∠CAB (Angles opposite to equal sides of a triangle)
∴ ∠BCA = 30°
Also, ∠BCD = 80°
∴ ∠BCA + ∠ACD = 80°
⇒ 30° + ∠ACD = 80°
∠ACD = 50°
i.e. ∠ECD = 50°
![]()
Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
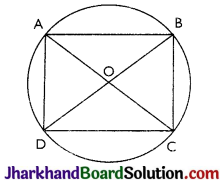
Answer:
Given: ABCD is a cyclic quadrilateral, whose diagonals AC and BD are diameters of the circle passing through A, B, C and D.
To prove: ABCD is a rectangle
Proof: In AAOD and ACOB AO = CO (Radii of a circle)
OD = OB (Radii of a circle)
∠AOD = ∠COB (Vertically opposite angles)
∴ ∆AOD ≅ ∆COB (By SAS axiom)
∴ ∠AOD S ∠OCB (By CPCT )
∴ AD || BC Similarly AB || CD Hence quadrilateral ABCD is a parallelogram.
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
(Angles in the semi-circle)
Thus, ABCD is a parallelogram with each internal angle as 90°. So, ABCD is a rectangle.
Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
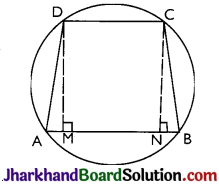
Answer:
Given: ABCD is a trapezium where non-parallel sides AD and BC are equal.
Construction: DM and CN are perpendiculars drawn on AB from D and C respectively.
To prove: ABCD is cyclic trapezium.
Proof: In ∆DAM and ∆CBN,
AD = BC (Given)
∠AMD = ∠BNC = 90° (By construction) DM = CN (Distance between the parallel lines)
∆DAM ≅ ∆CBN by RHS congruence criterion.
Now, ∠A = ∠B by CPCT
Also, ∠B + ∠C = 180° (sum of the co-interior angles)
⇒ ∠A + ∠C = 180°
In trapezium ABCD,
∠A + ∠B + ∠C + ∠D = 360°
=> 180° + ∠B + ∠D = 360°
⇒ ∠B + ∠D = 360° – 180°
= 180°
Thus, ABCD is a cyclic trapezium as sum of the pair of opposite angles is 180°.
Page-186
Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig). Prove that ∠ACP = ∠QCD.
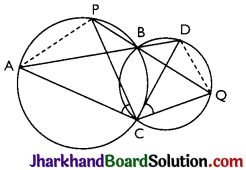
Answer:
Chords AP and DQ are joined.
For chord AP,
∠PBA = ∠ACP
(Angles in the same segment) …(i)
For chord DQ,
∠DBQ = ∠QCD
(Angles in same segment) …(ii)
ABD and PBQ are line segments intersecting at B.
∠PBA = ∠DBQ
(Vertically opposite angles) …(iii)
By the equations (i), (ii) and (iii),
∠ACP = ∠QCD
![]()
Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
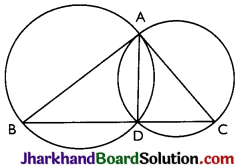
Answer:
Given: Two circles are drawn on the sides AB and AC of the triangle ΔABC as diameters. The circles intersected at D.
Construction: AD is joined.
To prove: D lies on BC. We have to prove that BDC is a straight line.
Proof: ∠ADB = ∠ADC = 90° (Angle in the semi circle)
Now, ∠ADB + ∠ADC = 90° + 90° = 180°
⇒ BDC is straight line.
Thus, D lies on the side BC.
Question 11.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
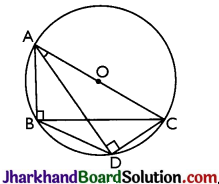
Answer:
Given: AC is the common hypotenuse.
∠ABC = ∠ADC = 90°.
To prove: ∠CAD = ∠CBD
Proof: Since, ∠ABC and ∠ADC are 90°.
These angles are in the semi circle. Thus, both the triangles are lying in the semi circle and AC is the diameter of the circle.
⇒ Points A, B, C and D are concyclic.
Thus, CD is the chord.
⇒ ∠CAD = ∠CBD (Angles in the same segment of the circle)
Question 12.
Prove that a cyclic parallelogram is a rectangle.
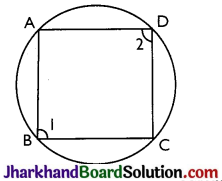
Answer:
Given: ABCD is a cyclic parallelogram.
To prove: ABCD is rectangle.
Proof: ∠1 + ∠2 = 180° (Opposite angles of a cyclic parallelogram)
also, opposite angles of a parallelogram are equal.
Thus,
∠1 = ∠2
⇒ ∠1 + ∠1 = 180°
⇒ ∠1 = 90°
One of the interior angles of the parallelogram is right angle. Thus, ABCD is a rectangle.