Jharkhand Board JAC Class 9 Maths Solutions Chapter 1 संख्या पद्धति Ex 1.4 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 1 संख्या पद्धति Exercise 1.4
प्रश्न 1.
उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए ।
हल:
हम यह जानते हैं कि 3.765, 3 और 4 के बीच में ही स्थित है। अत: 3 और 4 के बीच की दूरी को 10 बराबर भागों में विभाजित करके [3.7, 3.8] को लेंस से देखने पर स्पष्ट हो जाता है कि संख्या 3.765, 3.7 और 3.8 के बीच में स्थित है [ आकृति (A)]। अब हम नये वर्ग [3.1, 3.2], [3.2, 3.3], …, [3.9, 4] की दूरी को 10 बराबर भागों में बाँटेंगे। इससे स्पष्ट है कि 3.765 वर्ग [3.76, 3.77] के बीच में स्थित है। [आकृति (B)]।
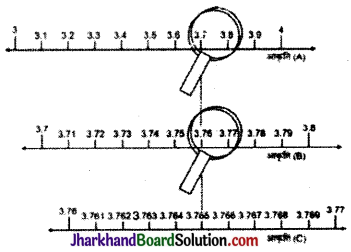
अतः निरन्तर उपयुक्त आवर्धन से सांत दशमलव संख्या रेखा पर निरूपित की जा सकती है और अब असांत वास्तविक संख्या, संख्या रेखा पर निरूपण की स्थिति में है।
![]()
प्रश्न 2.
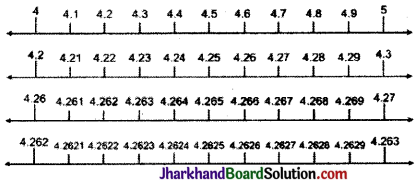
4 दशमलव स्थानों तक संख्या रेखा पर 4.26 को देखिए।
हल:
स्पष्ट है कि संख्या \(4 . \overline{26}\) संख्या रेखा पर 4 और 5 के मध्य स्थित है। इस एकक इकाई को 10 बराबर भागों में विभाजित करने पर 4.1 4.2, 4.3… प्राप्त होता है पुनः \(4 . \overline{26}\), विभाजन से प्राप्त 4.2 तथा 4.3 के मध्य स्थित है। पुनः 4.2 तथा 4.3 के मध्य की एकक इकाई दूरी को 4.21, 4.22, 4.23,…..4.29, भागों में विभाजित करके पुनः आवर्धन तथा वर्ग की दूरी को कम करने पर स्पष्ट होता है कि \(4 . \overline{26}\) संख्या 4.262 की अपेक्षा 4.264 के सन्निकट है।
\(4 . \overline{26}\) वर्ग [4.26, 4.27] जिसकी लम्बाई 0.01 है, में स्थित है। 4.26 को 0.001 की दूरी में दर्शाने के लिए हम दोबारा प्रत्येक वर्ग को 10 बराबर भागों में बाँटेंगे और 0.001 लम्बाई वाले वर्ग [4.262, 4.263] में दर्शायेंगे और हम देखेंगे कि \(4 . \overline{26}\), 4.262 की तुलना में 4.264 के नजदीक है।
इस प्रकार आवर्धन और वर्ग की लम्बाई घटाकर अनन्त तक यह क्रिया दोहराई जा सकती है। जिसमें \(4 . \overline{26}\) स्थित है।