JAC Class 9 Maths Solutions Chapter 2 बहुपद Ex 2.5

Jharkhand Board JAC Class 9 Maths Solutions Chapter 2 बहुपद Ex 2.5 Textbook Exercise Questions and Answers.

JAC Board Class 9 Maths Solutions Chapter 2 बहुपद Exercise 2.5

प्रश्न 1.
उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित के गुणनफल ज्ञात कीजिए :
(i) (x + 4 ) (x + 10)
(ii) (x + 8 ) (x – 10)
(iii) (3x + 4 ) (3x – 5)
(iv) \(\left(y^2+\frac{3}{2}\right)\left(y^2-\frac{3}{2}\right)\)
(v) (3 – 2x) (3 + 2x).
हल:
(i) (x + 4 ) (x + 10)
सर्वसमिका
(x + a) (x + b) = x² + (a + b)x + ab
= x² + (4 + 10 )x + 10 × 4
= x² + 14x + 40.

(ii) (x + 8) (x – 10)
सर्वसमिका
[(x + a) (x + b) = x² + (a + b)x + ab]
= x² + (8 – 10)x + 8 × (-10)
= x – 2x – 80.

(iii) (3x + 4) (3x – 5) = 3x(3x – 5) + 4(3x – 5 )
= 9x² – 15x + 12x – 20
= 9x² – 3x – 20.

(iv) \(\left(y^2+\frac{3}{2}\right)\left(y^2-\frac{3}{2}\right)\)
सर्वसमिका
(a + b) (a – b) = (a)² – (b)² से
= (y²)² – (\(\frac{3}{2}\))² = y⁴ – \(\frac{9}{4}\)

(v) सर्वसमिका (x + y) (x – y) = x² – y² से
(3 – 2x) (3 + 2x) = (3)² – (2x)²
= 9 – 4x²

प्रश्न 2.
सीधे गुणा किए बिना निम्नलिखित गुणनफलों के मान ज्ञात कीजिए :
(i) 103 × 107
(ii) 95 × 96
(iii) 104 × 96.
हल:
(i) सर्वसमिका
(x + a) (x + b) = x² + (a + b) + ab
103 × 107 = (100 + 3) (100 + 7)
= (100)² + (3 + 7) (100) + 3 × 7
= 10000 + 1000 + 21
= 11021.

(ii) सर्वसमिका
(x + a)(x + b) = x² + (a + b) + ab
95 × 96 = (100 – 5) (100 – 4)
= (100)² + (- 5 – 4) (100) + (-5) × (-4)
10000 – 900 + 20 = 9120.

(iii) सर्वसमिका (a + b) (a – b) = a² – b²
104 × 96 = (100 + 4) (100 – 4)
= (100)² – (4)²
= 10000 – 16 = 9984.

प्रश्न 3.
उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित के गुणनखण्ड कीजिए:
(i) 9x² + 6xy + y²
(ii) 4y² – 4y + 1
(iii) x² – \(\frac{y^2}{100}\)
हल:
(i) 9x² + 6xy + y²
सर्वसमिका
a² + 2ab + b² = (a + b)²
= (3x)² + 2 × 3x × y + (y)²
= (3x + y)².

(ii) 4y² – 4y + 1
सर्वसमिका a² – 2ab + b² = (a – b)²
= (2y)² – 2 × 2y × 1 + (1)².
= (2y – 1)².

(iii) x² – \(\frac{y^2}{100}\) = \((x)^2-\left(\frac{y}{10}\right)^2\)
[सर्वसमिका a² – b² = (a + b)(a – b) से]
= \(\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)

प्रश्न 4.
उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित में से प्रत्येक का प्रसार कीजिए:
(i) (x + 2y + 4z)²
(ii) (2x – y + z)²
(iii) (-2x + 3y + 2z)²
(iv) (3a – 7b – c)²
(v) (-2x + 5y – 3z)²
(vi) \(\left[\frac{1}{4} a-\frac{1}{2} b+1\right]^2\)
हल:
(i) (x + 2y + 4z)²
सर्वसमिका (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx से
= (x)² + (2y)² + (4z)² + 2(x)(2y) + 2(2y) (4z) + 2(4z) (x)
= x² + 4y² + 16z² + 4xy + 16yz + 8zx.

(ii) (2x – y + z)²
सर्वसमिका (x + y + z)² = (x² + y² + z²) + 2xy + 2yz + 2zx
= (2x)² + (y)² + (z)² + 2(2x) (-y) + 2(-y) (z) + 2(z) (2x)
= 4x² + y² + z² – 4xy – 2yz + 4xz.

(iii) (-2x + 3y + 2z)²
सर्वसमिका (x + y + z)² = (x² + y² + z²) + 2xy + 2yz + 2zx
= (-2x)² + (3y)² + (2z)² + 2(-2x) (3y) + 2(3y) (2z) + 2(2z) (-2x)
= 4x² + 9y² + 4z² – 12xy + 12yz – 8zx.

(iv) (3a – 7b – c)²
सर्वसमिका (x + y + z)² = (x² + y² + z²) + 2xy + 2yz + 2zx
= (3a)² + (-7b)² + (-c)² + 2(3a) (-7b) + 2(-7b) (-c) + 2(-c) (3a)
= 9a² + 49b² + c² – 42ab + 14bc – 6ca.

(v) (-2x + 5y – 3z)²
सर्वसमिका (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
= (-2x)² + (5y)² + (-3z)² + 2(-2x) (5y) + 2(5y) (-3z) + 2(-3z) (-2x)
= 4x² + 25y² + 9z² – 20xy – 30yz + 12zx.

(vi) \(\left[\frac{1}{4} a-\frac{1}{2} b+1\right]^2\)
सर्वसमिका (x + y + z)² = (x² + y² + z²) + 2xy + 2yz + 2zx

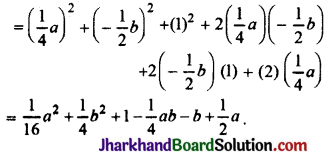
प्रश्न 5.
गुणनखण्ड कीजिए:
(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz
(ii) 2x² + y² + 8z² – 2\(\sqrt{2}\)xy + 4\(\sqrt{2}\)yz – 8xz
हल:
(i) 4x² + 9y² + 16z² + 12xy – 24yz – 16xz
= (2x)² + (3y)² + (-4z)² + 2(2x) (3y) + 2(3y)(-4z) + 2(2x)(-4z)
सर्वसमिका [∵ x² + y² + z² + 2xy + 2yz + 2xz = (x + y + z)²] से
= [2x + 3y + (-4z)]²
= (2x + 3y – 4z)².

(ii) 2x² + y² + 8z² – 2\(\sqrt{2}\)xy + 4\(\sqrt{2}\)yz – 8xz
सर्वसमिका (x + y + z² = x² + y² + z² + 2xy + 2yz + 2zx
= (\(\sqrt{2}\)x)² + (-y)² + (-2\(\sqrt{2}\)z)² + 2(\(\sqrt{2}\)x) (-y) + 2(-y)(-2\(\sqrt{2}\)z) + 2(\(\sqrt{2}\)x)(-2\(\sqrt{2}\)z)
= [\(\sqrt{2}\)x + (y) + (2\(\sqrt{2}\)z)]²
= (\(\sqrt{2}\)x – y – 2\(\sqrt{2}\)z)²

प्रश्न 6.
निम्नलिखित घनों को प्रसारित रूप में लिखो :
(i) (2x + 1)³
(ii) (2a – 3b)³
(iii) \(\left[\frac{3}{2} x+1\right]^3\)
(iv) \(\left[x-\frac{2}{3} y\right]^3\)
हल:
(i) सर्वसमिका
(a + b)³ = a³ + b³ + 3a²b + 3ab² से
(2x + 1)³ = (2x)³ + (1)³ + 3(2x)² (1) + 3(2x) (1)²
= 8x³ + 1 + 12x² + 6x
= 8x³ + 12x² + 6x + 1.

(ii) सर्वसमिका
(x – y)³ = x³ – y³ – 3x²y + 3xy² से
(2a – 3b)³ = (2a)³ – (3b)³ – 3(2a)² (3b) + 3(2a) (3b)²
= 8a³ – 27b³ – 36a²b + 54ab²
= 8a³ – 36a²b + 54ab² – 27b³.

(iii) सर्वसमिका
(x + y)³ = x³ + y³ + 3x²y + 3xy²

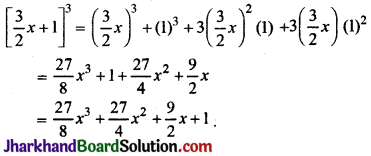
(iv) सर्वसमिका
(x – y)³ = x³ – y³ – 3x²y + 3xy²

प्रश्न 7.
उपयुक्त सर्वसमिकाएँ प्रयोग करके निम्नलिखित के मान ज्ञात कीजिए :
(i) (99)³
(ii) (102)³
(iii) (998)³.
हल:
(i) सर्वसमिका
(x – y)³ = x³ – y³ – 3xy(x – y) से
∴ (99)³ = (100 – 1)³
= (100)³ – (1)³ – 3 × 100 × 1(100 – 1)
= 1000000 – 1 – 300(99)
= 1000000 – 1 – 29700
= 970299.

(ii) सर्वसमिका
(x + y)³ = x³ + y³ + 3xy(x + y) से
(102)³ = (100 + 2)³
= (100)³ + (2)³ + 3(100) (2) (100 + 2)
= 1000000 + 8 + 600 × 102
= 1000000 + 8 + 61200
= 1061208.

(iii) सर्वसमिका
(x – y)³ = x³ – y³ – 3xy(x – y) से
(998)³ = (1000 – 2)³
(1000)³ – (2)³ – 3 × 1000 × 2(1000 – 2)
= 1000000000 – 8 – 6000 × 998
= 1000000000 – 8 – 5988000
= 994011992.

प्रश्न 8.
निम्नलिखित में से प्रत्येक का गुणनखण्डन कीजिए :
(i) 8a³ + b³ + 12a²b + 6ab²
(ii) 8a³ – b³ – 12a²b + 6ab²
(iii) 27 – 125a³ – 135a + 225a²
(iv) 64a³ – 27b³ – 144a²b + 108ab²
(v) 27p³ – \(\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p\)
हल:
(i) 8a³ + b³ + 12a²b + 6ab²
= 8a³ + b³ + 6ab(2a + b)
= (2a)³ + b³ + 3(2a) (b) (2a + b)
= (2a + b)³
= (2a + b) (2a + b) (2a + b).

(ii) 8a³ – b³ – 12a²b + 6ab²
= 8a³ – b³ – 6ab(2a – b)
= (2a)³ – b³ – 3(2a)(b)(2a – b)
= (2a – b)³
= (2a – b)(2a – b)(2a – b).

(iii) 27 – 125a³ – 135a + 225a²
= 27 – 125a³ – 45a(3 – 5a)
= (3)³– (5a)³ – 3 × 3 × 5a(3 – 5a)
= (3 – 5a)³
= (3 – 5a) (3 – 5a) (3 – 5a).

(iv) 64a³ – 27b³ – 144a²b + 108ab²
= 64a³ – 27b³ – 36ab(4a – 3b)
= (4a)³ – (3b)³ – 3 × 4a × 3b(4a – 3b)
= (4a – 3b)³
= (4a – 3b) (4a – 3b) (4a – 3b).

(v) 27p³ – \(\frac{1}{216}-\frac{9}{2} p^2+\frac{1}{4} p\)

प्रश्न 9.
सत्यापित कीजिए :
(i) x³ + y³ = (x + y) (x² – xy + y²)
(ii) x³ – y³ = (x – y) (x² + xy + y²).
हल:
(i) x³ + y³ = (x + y) (x² – xy + y²)
दायाँ पक्ष = (x + y) (x² – xy + y²)
= x(x² – xy + y²) + (x² – xy + y²)
= x³ – x²y + y²x + yx² – xy²+ y³
= x³ + y³ = बायाँ पक्ष। इति सिद्धम्

(ii) x³ – y³ = (x – y) (x² + xy + y²)
दायाँ पक्ष = (x – y) (x² + xy + y²)
= x(x² + xy + y²) – y(x² + xy + y²)
= x³ + x²y + xy² – yx² – xy² – y³
= x³ – y³ = बायाँ पक्ष। इति सिद्धम्

प्रश्न 10.
निम्नलिखित में से प्रत्येक का गुणनखण्ड कीजिए:
(i) 27y³ + 125z³,
(ii) 64m – 343n³
हल:
(1) 27y³ + 125z³ = (3y)³ + (5z)³
सर्वसमिका
x² + y³ = (x + y) (x² – xy + y²) से
= (3y + 5z) [(3y)² – (3y)(5z) + (5z)²]
= (3y + 5z)(9y² – 15yz + 25z²).

(ii) सर्वसमिका
x³ – y³3 = (x – y) (x² + xy + y²)
64m³ – 343n³ = (4m)³ – (7n)³
= (4m – 7n) [(4m)² + (4m)(7n) + (7n)²]
= (4m – 7n)(16m² + 28mn + 49n²).

प्रश्न 11.
गुणनखण्ड कीजिए :
27x³ + y³ – 9xyz.
हल:
27x³ + y³ + z³ – 9xyz
सर्वसमिका
x³ + y³ + z³(-3xyz) = (x + y + z) (x² + y² + z² – xy – yz – zx)
= (3x)³ + (y)³ + (z)³ – 3(3x)(y)(z)
= (3x + y + z) [(3x)² + (y)² + (z)² – (3x)y – yz – z(3x)]
= (3x + y + z)(9x² + y² + z² – 3xy – yz – 3zx).

प्रश्न 12.
सत्यापित कीजिए x³ + y³ + z³ – 3xyz = \(\frac{1}{2}\)(x + y + z) [(x – y)² + ( y – z)² + (z – x)²]
हल:
दायाँ पक्ष = \(\frac{1}{2}\)(x + y + z) [(x – y)² + (y – z)² + (z – x)²]
= \(\frac{1}{2}\)(x + y + z)(x² – 2xy + y² + y² – 2yz + z² + z² – 2zx + x²)
= \(\frac{1}{2}\)(x + y + z)(2x² + 2y² + 2z² – 2xy – 2yz – 2zx)
= (x + y + z)(x² + y² + z² – xy – yz – zx)
[∵ a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)]
सर्वसमिका से
= x³ + y³ + z³ – 3xyz
= बायाँ पक्ष इति सिद्धम् ।

प्रश्न 13.
यदि x + y + z = 0 हो, तो दिखाइए कि x³ + y³ + z³ = 3xyz है।
हल:
दिया है, x + y + z = 0 ⇒ x + y = -z
दोनों पक्षों का घन लेने पर,
(x + y)³ = (-z)³
⇒ x³ + y³ + 3xy(x + y) = -z³ (∵ x + y = -z)
⇒ x³ + y³ + 3xy(-z) = -z³
⇒ x³ + y³ + z³ = 3xyz, इति सिद्धम्।

प्रश्न 14.
वास्तव में घनों का परिकलन किए बिना निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए:
(i) (-12)³ + (7)³ + (5)³
(ii) (28)³ + (-15)³ + (-13)³.
हल:
(i) (-12)³ + (7)³ + (5)³
माना x = -12, y = 7, z = 5
यदि x + y + z = 0, तो x³+ y³ + z³ = 3xyz
⇒ -12 + 7 + 5 = 0
∵ सर्वसमिका x³ + y³ + z³ = 3xyz से
∴ (-12)³ + (7)³ + (5)³ = 3 × 3(-12) × 7 × 5
= -1260.

(ii) 28³ + (-15)³ + (-13)³
28 + (-15) + (-13) = 28 – 28 = 0
अतः 28³ + (-15)³ + (-13)³
= 3 × 28 × (-15) × (-13 )
= 16380.

प्रश्न 15.
नीचे दिए गए आयतों, जिनमें उनके क्षेत्रफल दिए गए हैं, में से प्रत्येक की लम्बाई और चौड़ाई के लिए सम्भव व्यंजक दीजिए:

हल:
आयत की लम्बाई और चौड़ाई क्षेत्रफल के गुणनखण्ड होंगे।
(i) आयत का क्षेत्रफल = लम्बाई × चौड़ाई
क्षेत्रफल = 25a² – 35a + 12
= 25a² – 15a – 20a + 12
= 5a (5a – 3) – 4(5a – 3)
= (5a – 3) (5a – 4)
∴ यदि लम्बाई (5a – 3) तो चौड़ाई = (5a – 4) तो चौड़ाई
और यदि लम्बाई = (5a – 4) तो चौड़ाई = (5a – 3) इकाई

(ii) क्षेत्रफल 35y² + 13y – 12
= 35y² + 28y – 15y – 12
= 7y (5y + 4) – 3(5y + 4)
= (5y + 4)(7y – 3)
∴ यदि लम्बाई = (5y + 4) तो चौड़ाई = (7y – 3) तो चौड़ाई
इकाई और यदि लम्बाई = (7y – 3) तो चौड़ाई = (5y + 4) इकाई.

प्रश्न 16.
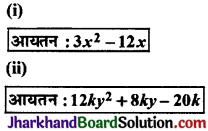
घनाभ (cuboids), जिनके आयतन नीचे दिए गए हैं की विमाओं के लिए संभव व्यंजक क्या हैं ?

हल:
संभवत: घनाभों की भुजाएँ आयतन के गुणनखण्ड होंगे।
घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
(i) आयतन = 3x² – 12x = 3x(x – 4)
= 3 × x × (x – 4)
अतः संभवत: घनाभ की भुजाएँ क्रमश: 3, x और (x – 4) इकाई हैं।

(ii) आयतन = 12ky² + 8ky – 20k
= 4k(3y² + 2y – 5)
= 4k[3y² + 5y – 3y – 5]
= 4k[(3y + 5) – 1(3y + 5)]
= 4k(3y + 5) (y – 1)
= 4k × (3y + 5) × (y – 1)
अतः सम्भवत: घनाभ की भुजाएँ क्रमश: 4k, (3y + 5) और (y – 1) हैं।