Jharkhand Board JAC Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Exercise 9.2
प्रश्न 1.
आकृति में, ABCD एक समान्तर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।
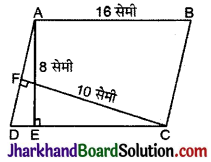
हल:
समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
∴ समान्तर चतुर्भुज ABCD का क्षेत्रफल
= DC × AE (∵ AB = CD)
= AB × AE
= (16 × 8) सेमी2 = 128 सेमी2 ……….(i)
पुनः समान्तर चतुर्भुज ABCD में AD = BC, AD || BC के बीच की दूरी CF हो, तो
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AD × CF
= (AD × 10) सेमी2 …..(ii)
समीकरण (i) एवं (ii) से,
AD × 10 = 128
∴ AD = \(\frac{128}{10}\) = 12.8 सेमी।
![]()
प्रश्न 2.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य बिन्दु हैं, तो दर्शाइए कि :
ar (EFGH) = \(\frac{1}{2}\)ar (ABCD).
हल:
दिया है : ABCD एक समान्तर चतुर्भुज है जिसमें बिन्दु E, F, G और H क्रमशः समान्तर चतुर्भुज की भुजाओं AB, BC, CD व DA के मध्य-बिन्दु हैं।
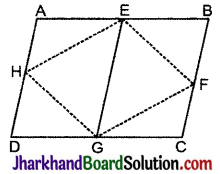
सिद्ध करना है: ar (||gm EFGH) = \(\frac{1}{2}\)ar (||gm ABCD)
रचना: E और G को मिलाया।
उपपत्ति: ∵ ☐ABCD एक समान्तर चतुर्भुज है।
∴ AB = CD और AB || CD
∵ E, AB का मध्य-बिन्दु है और G, CD का मध्य-बिन्दु है।
AE = EB = \(\frac{1}{2}\)AB
और DG = GC = \(\frac{1}{2}\)CD
तब AE = DG और AE || DG
∴ ☐AEGD एक समान्तर चतुर्भुज है।
∵ ☐AEGD और ΔEGH उभयनिष्ठ आधार EG पर स्थित हैं। इनके शीर्ष A, D व H एक ही रेखा पर हैं जो EG के समान्तर है।
∴ ΔEGH का क्षेत्रफल = \(\frac{1}{2}\)समान्तर चतुर्भुज AEGD का क्षेत्रफल …. (1)
इसी प्रकार,
ΔEGF का क्षेत्रफल
= \(\frac{1}{2}\)समान्तर चतुर्भुज EBCG का क्षेत्रफल ….. (2)
समीकरण (1) व (2) को जोड़ने पर,
ΔEGH का क्षेत्रफल ΔEGF का क्षेत्रफल
= \(\frac{1}{2}\)समान्तर चतुर्भुज AEGD का क्षेत्रफल + \(\frac{1}{2}\)समान्तर चतुर्भुज EBCG का क्षेत्रफल
∴ ☐EFGH का क्षेत्रफल = \(\frac{1}{2}\),
[||gm AEGD का क्षेत्रफल + ||gm BECG का क्षेत्रफल]
= \(\frac{1}{2}\)समान्तर चतुर्भुज ABCD का क्षेत्रफल
अतः ar (||gm EFGH) = \(\frac{1}{2}\)ar (||gm ABCD).
इति सिद्धम्।
प्रश्न 3.
P और Q क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं दर्शाइए कि :
ar (ΔAPB) = ar (BQC).
हल:
ΔAPB और समान्तर चतुर्भुज ABCD समान आधार AB पर और समान्तर रेखाओं AB और DC के मध्य स्थित हैं।
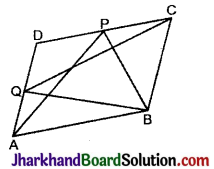
∴ ar (ΔAPB) = \(\frac{1}{2}\) ar (||gm ABCD) …..(i)
इसी प्रकार, ΔBQC और समान्तर चतुर्भुज ABCD समान आधार BC और समान समान्तर रेखाओं BC और AD के मध्य स्थित हैं।
∴ ar (ΔBQC) = \(\frac{1}{2}\)ar (||gm ABCD) …….(ii)
∴ समीकरण (i) एवं (ii) से,
ar (ΔAPB) = ar (ΔBQC) इति सिद्धम्।
![]()
प्रश्न 4.
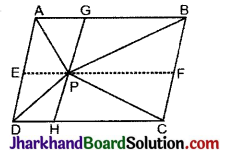
आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिन्दु है। दर्शाइये कि:
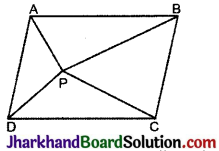
(i) ar (ΔAPB) + ar (ΔPCD) = \(\frac{1}{2}\)ar (||gm ABCD)
(ii) ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD)
हल:
AB व DC के समान्तर रेखाखण्ड EPF खींचा और AD व BC के समान्तर रेखाखण्ड GPH खींचा।
अब AGHD एक समान्तर चतुर्भुज है।
[∵ GH || DA और AG || DH]
इस प्रकार, HCBG, EFCD तथा ABFE समान्तर चतुर्भुज हैं।
(i) ΔAPB और समान्तर चतुर्भुज ABFE समान आधार AB पर और समान समान्तर रेखाओं AB और DC के मध्य स्थित हैं।
∴ ar (ΔAPB) = \(\frac{1}{2}\)ar(||gm ABFE) ….(i)
इसी प्रकार,
ar (ΔPCD) = \(\frac{1}{2}\)ar(||gm ECD) …..(ii)
∴ समीकरण (i) और (ii) को जोड़ने पर,
ar (ΔAPB) + ar (ΔPCD) = \(\frac{1}{2}\) [ar (||gm ABFE) + ar (||gm EFCD)]
= \(\frac{1}{2}\)ar (||gm ABCD) …..(iii)
इति सिद्धम्।
(ii) ΔAPD और समान्तर चतुर्भुज AGHD समान आधार AD पर और समान समान्तर रेखाओं AD और HG के मध्य स्थित हैं।
∴ ar (ΔAPD) = \(\frac{1}{2}\)ar (||gm AGHD) …..(iv)
इसी प्रकार,
ar (ΔPBC) = \(\frac{1}{2}\)ar (||gm GBCH) ……(v)
∵ समीकरण (iv) और (v) को जोड़ने पर
ar (ΔAPD) + ar (ΔPBC) = \(\frac{1}{2}\)[ar (||gm GHD)+ar (GBCH)]
= \(\frac{1}{2}\)ar (||gm ABCD) ……(vi)
समीकरण (iii) एवं (vi) से,
ar (ΔAPD) + ar (ΔPBC) = ar (ΔAPB) + ar (ΔPCD). इति सिद्धम्।
प्रश्न 5.
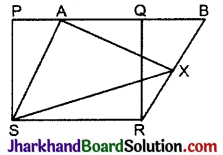
आकृति में, PQRS और ABRS समान्तर चतुर्भुज तथा X भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि:
(i) ar (||gm PQRS) = ar (||gm ABRS)
(ii) ar (ΔAXS) = \(\frac{1}{2}\)ar (||gm PQRS).
हल:
(i) समान्तर चतुर्भुज PQRS और समान्तर चतुर्भुज ABRS समान आधार RS पर और समान समान्तर रेखाओं SR तथा PB के बीच स्थित हैं।
∴ ar (||gm PQRS) = ar (||gm ABRS) …..(i)
इति सिद्धम्।
(ii) ΔAXS और समान्तर चतुर्भुज ABRS समान आधार 45 पर और समान समान्तर रेखाओं AS और RB के बीच स्थित हैं।
∴ ar (ΔAXS) = \(\frac{1}{2}\)ar (||gm ABRS)
⇒ ar (ΔAXS) = \(\frac{1}{2}\)ar (||gm PQRS)
[भाग (i) से] इति सिद्धम्।
![]()
प्रश्न 6.
एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का एक खेत है। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है ? इन भागों के आकार क्या हैं ? वह किसान खेत में गेहूं और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है वह ऐसा कैसे कर सकता है ?
हल:
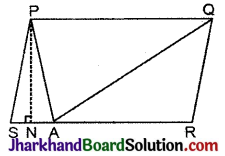
माना किसान के पास चित्रानुसार PQRS समान्तर चतुर्भुज के आकार का एक खेत है। किसान ने भुजा RS पर एक बिन्दु चुनकर उस P तथा Q से मिला दिया।
खेत तीन त्रिभुजाकार भागों में विभाजित हो गया है। ये भाग ΔPSA, ΔPAQ तथा ΔQAR हैं।
∵ किसान को गेहूँ और दालें बराबर क्षेत्रफलों में बोनी हैं, इसलिए P से सम्मुख भुजा SR पर PN लम्ब डाला गया है।
ΔPAQ का क्षेत्रफल = \(\frac{1}{2}\)PQ × PN
∵ PQRS एक समान्तर चतुर्भुज है। ∴ PQ = RS
तब ΔPAQ का क्षेत्रफल = \(\frac{1}{2}\)RS × PN, (∵ PQ = RS)
∴ ΔPAQ का क्षेत्रफल = \(\frac{1}{2}\)(SA + AR) × PN
= \(\frac{1}{2}\)SA × PN + \(\frac{1}{2}\)AR \(\frac{1}{2}\) × PN
= ΔPSA का क्षेत्रफल + ΔQAR का क्षेत्रफल
अतः किसान को ΔPAQ क्षेत्रफल में गेहूँ और ΔPSA
तथा ΔQAR के क्षेत्रफल में दालें बोनी चाहिए।