Jharkhand Board JAC Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.5 Textbook Exercise Questions and Answers.
JAC Board Class 9 Maths Solutions Chapter 10 वृत्त Exercise 10.5
प्रश्न 1.
आकृति में, केन्द्र O वाले वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° हैं। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है, तो ∠ADC ज्ञात कीजिए।
हल:
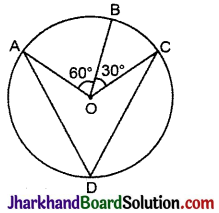
∵ एक वृत्त के केन्द्र पर चाप ABC, ∠AOC = ∠AOB + ∠BOC = 60° + 30° = 90° तथा ∠ADC वृत्त के बचे हुए भाग के एक बिन्दु पर बनता है।
∠ADC = \(\frac{1}{2}\)(∠AOC)
= \(\frac{1}{2}\) × 90° = 45°.
प्रश्न 2.
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अंतरित कोण ज्ञात कीजिए।
हल:
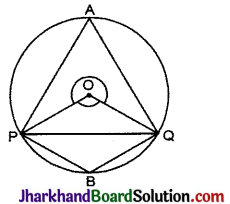
माना PQ एक जीवा है। OP तथा OQ को मिलाया।
दिया है: PQ = OP = OQ [∵ जीवा = त्रिज्या]
ΔOPQ एक समबाहु त्रिभुज है।
∴ ∠POQ = 60°
∵ चाप PAQ वृत्त के केन्द्र पर अंतरित (वृहत्)
∠POQ = 360° – 60°
= 300°
∴ ∠PBQ वृत्त के लघु चाप पर बना कोण
∠PBQ = \(\frac{1}{2}\) × दीर्घ ∠POQ
= \(\frac{1}{2}\) × 300° = 150°
इसी प्रकार, दीर्घ चाप पर बना कोण
∠PAQ = \(\frac{1}{2}\) लघु (∠POQ) = \(\frac{1}{2}\) × 60° = 30°.
∴ जीवा द्वारा लघु चाप पर बनाया गया कोण 15000 तथा दीर्घ चाप पर बनाया गया कोण 30° है।
![]()
प्रश्न 3.
आकृति में, ∠PQR 100° है, जहाँ P, Q तथा R; केन्द्र O वाले एक वृत्त पर स्थित बिन्दु हैं। ∠OPR ज्ञात कीजिए।
हल:
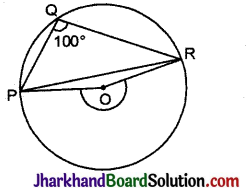
चाप \(\overparen{P R}\) द्वारा केन्द्र पर अन्तरित कोण POR तथा शेषभाग पर अंतरित ∠PQR
∴ वृहत् ∠POR = 2∠POR
⇒ वृहत् ∠POR = 2 × 100° = 200°
लघु ∠POR = 360° – 200° = 160°
ΔOPR में, OP = OR [ एक ही वृत्त की त्रिज्याएँ]
⇒ ∠OPR = ∠ORP = x° (माना)
(समान भुजाओं के सम्मुख कोण)
ΔOPR में,
∠POR + ∠OPR + ∠ORP = 180°
⇒ 160° + x° + x° = 180°
⇒ 2x° = 180° – 160°= 20°
∴ x° = \(\frac{1}{2}\) = 100°
अतः ∠OPR = 100°.
प्रश्न 4.
आकृति में, ∠ABC = 69° और ∠ACB = 31° हों, तो ∠BDC ज्ञात कीजिए।
हल:
ΔABC में
∠BAC + ∠ABC + ∠BCA = 180°
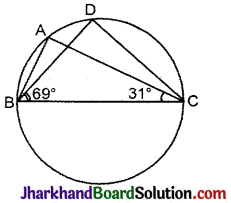
∠BAC + 69° + 31° = 180°
∠BAC + 100° = 180°
∴ ∠BAC = 180° – 100° = 80°
∵ एक ही वृत्तखण्ड में कोण बराबर होते हैं।
∴ ∠BDC = ∠BAC = 80°.
![]()
प्रश्न 5.
आकृति में एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° हैं। ∠BAC ज्ञात कीजिए।
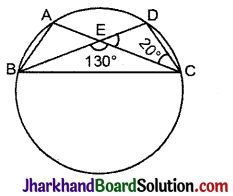
हल:
∠CED + ∠CEB = 180° [ रैखिक युग्म]
⇒ ∠CED + 130° = 180°
∴ ∠CED = 180° – 130° = 50°
ΔECD में
∠EDC + ∠CED + ∠ECD = 180°
⇒ ∠EDC + 50° + 20° = 180°
⇒ ∠EDC = 180° – 50°- 20°
∴ ∠EDC = 110
∵ एक ही वृत्तखण्ड के कोण समान होते हैं।
∴ ∠BAC = ∠BDC = 110.
प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है, जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हों, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
हल:
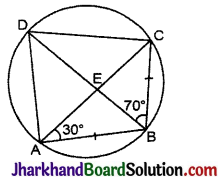
∠BDC = ∠BAC
[एक ही वृत्तखण्ड के कोण]
⇒ ∠BDC = 30°
[∵ ∠BAC = 30° (दिया है)]
ΔBCD में,
∠BDC + ∠DBC + ∠BCD = 180°,
⇒ 30° + 70° + ∠BCD = 180°
∠BCD = 180° – 30° – 70° = 80°
यदि AB = BC, तब ∠BCA = ∠BAC = 30°
[त्रिभुज में बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।]
अब ∠ECD = ∠BCD – ∠BCA
= 80° – 30° = 50°
[∵ ∠BCD = 80° (ऊपर ज्ञात किया) तथा ∠BCA = 30°]
∴ ∠BCD = 80° और ∠ECD = 50°.
प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीष से होकर जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
हल:
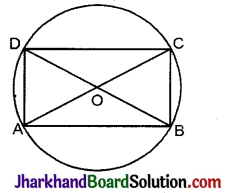
वृत्त C (O, r) में चक्रीय चतुर्भुज ABCD के व्यास AC = BD.
सिद्ध करना है: चतुर्भुज ABCD एक आयत है।
उपपत्ति: चूँकि एक वृत्त की सभी त्रिज्याएँ बराबर होती है।
∴ OA = OB = OC= OD
⇒ OA = OC = \(\frac{1}{2}\)AC ……(1)
व OB = OD = \(\frac{1}{2}\)BD ……(2)
समी. (1) व (2) से,
⇒ AC = BD
∵ चतुर्भुज ABCD के विकर्ण बराबर हैं तथा एक-दूसरे को समद्विभाजित करते हैं।
अतः चतुर्भुज ABCD एक आयत है।
![]()
प्रश्न 8.
यदि एक समलम्ब की असमान्तर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
हल:
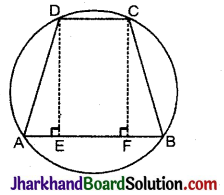
दिया है: एक समलम्ब ABCD की असमान्तर भुजाएँ AD = BC.
सिद्ध करना है: ABCD एक चक्रीय चतुर्भुज है।
रचना: DE ⊥ AB तथा CF ⊥ AB खींचे।
उपपत्ति:
ΔDEA तथा ΔCFB में,
∵ AD = BC [दिया है]
∠DEA = ∠CFB [प्रत्येक 90°]
तथा DE = CF [दो समान्तर रेखाओं के बीच की दूरी]
∴ ΔDEA ≅ ΔCFB (RHS प्रगुण)
⇒ ∠A = ∠B तथा ∠ADE = ∠BCF
अब ∠ADE = ∠BCF
⇒ 90° + ∠ADE = 90° + ∠BCF
(दोनों पक्षों में 90° जोड़ने पर)
∠EDC + ∠ADE = ∠FCD + ∠BCF
[∵ ∠EDC = 90° तथा ∠FCD = 90°]
⇒ ∠ADC = ∠BCD या ∠D = ∠C
अतः ∠A = ∠B तथा ∠C = ∠D
∴ ∠A + ∠B + ∠C + ∠D = 60°
(एक चतुर्भुज के अन्तः कोणों का योग 360° होता है)
⇒ 2∠B + 2∠D = 360°
⇒ ∠B + ∠D = 180°
∴ ABCD एक चक्रीय चतुर्भुज है। इति सिद्धम्।
प्रश्न 9.
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेदित करते हैं। B से जाने वाले दो रेखाखण्ड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेदित करते हुए खींचे गए हैं (देखिए आकृति)।
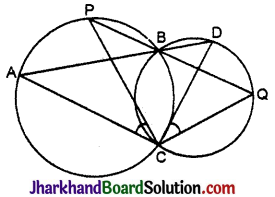
सिद्ध कीजिए कि ∠ACP = ∠QCD है।
हल:
∵ एक ही वृत्तखण्ड के कोण बराबर होते हैं।
∠ACP = ∠ABP ……(i)
और ∠QCD = ∠QBD ……(ii)
तथा ∠ABP = ∠QBD ……(iii)
[शीर्षाभिमुख कोण[
समीकरण (i), (ii) एवं (iii) से,
∴ ∠ACP = ∠QCD. इति सिद्धम्।
![]()
प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित होता है।
हल:
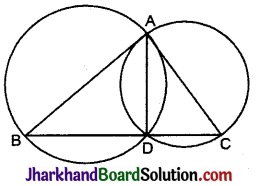
दिया है:
ΔABC की भुजाओं AB तथा AC को व्यास लेते हुए दो वृत्त बनाए गए हैं। वृत्त एक-दूसरे को A तथा D बिन्दु पर प्रतिच्छेदित करते हैं।
सिद्ध करना है: D, BC पर स्थित है।
रचना: A तथा D को मिलाया।
उपपत्ति: ∵ AB तथा AC वृत्तों के व्यास हैं। [दिया है]
∴ ∠ADB = 90° [अर्द्धवृत्त में बने कोण] …..(i)
⇒ ∠ADC = 90° [अर्द्धवृत्त में बने कोण] …..(ii)
समीकरण (i) और (ii) को जोड़ने पर,
∠ADB + ∠ADC = 90° + 90° = 180°
⇒ BDC एक सीधी रेखा है।
∴ D, BC पर स्थित है। इति सिद्धम्।
प्रश्न 11.
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠CAD = ∠CBD हैं।
हल:
उभयनिष्ठ कर्ण AC को व्यास मानकर खींचा गया वृत्तबिन्दु B तथा D से गुजरता है।
[∵ ∠ABC = ∠ADC = 90° है|
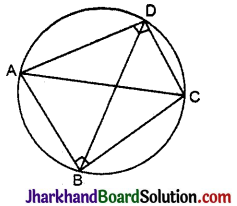
स्पष्टतः ∠CAD = ∠CBD
∵ एक ही वृत्तखण्ड में स्थित कोण समान होते हैं। इति सिद्धम्।
![]()
प्रश्न 12.
सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज आयत होता है।
हल:
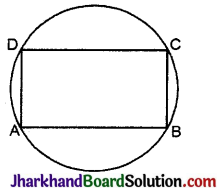
दिया है: चक्रीय समान्तर चतुर्भुज ABCD
सिद्ध करना है: ABCD एक आयत है।
उपपत्ति: ∵ ABCD एक चक्रीय समान्तर चतुर्भुज है।
∴ ∠A + ∠C = 180° ……(i)
लेकिन ∠A = ∠C ……(ii)
समीकरण (i) तथा (ii) से,
∠A = ∠C = 90°, [समान्तर चतुर्भुज के सम्मुख कोण]
इसी प्रकार, ∠B = ∠D = 90° है।
∴ ABCD का प्रत्येक कोण 90° है।
अत: ABCD एक आयत है। इति सिद्धम्।