JAC Class 10 Maths Important Questions Chapter 10 वृत्त

Jharkhand Board JAC Class 10 Maths Important Questions Chapter 10 वृत्त Important Questions and Answers.

JAC Board Class 10th Maths Important Questions Chapter 10 वृत्त

लघुत्तरात्मक / निबन्धात्मक प्रश्न :

प्रश्न 1.
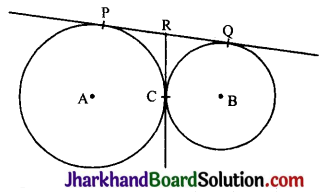
दी गई आकृति में, दो वृत्त परस्पर बिन्दु C पर स्पर्श करते हैं। सिद्ध कीजिए कि C पर खींची गई उभयनिष्ठ स्पर्श रेखा, P तथा Q पह खींची गई उभयनिष्ठ स्पर्श रेखा का समद्विभाजन करती हैं।

हल:
दिया है : दो वृत्त जिनके केन्द्र A तथा B हैं परस्पर बिन्दु C पर स्पर्श करते हैं।
सिद्ध करना है: C पर खींची गई स्पर्श रेखा, P तथा Q पर खींची गई स्पर्श रेखा का समद्विभाजन करती है।
उपपत्ति: हम जानते हैं कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
PR = RC …..(1)
(बिन्दु R से केन्द्र A वाले वृत्त पर खींची गई स्पर्श रेखाएँ)
तथा RQ = RC …..(2)
(बिन्दु R से केन्द्र B वाले वृत्त पर खींची गई स्पर्श रेखाएँ)
समी (1) व (2) से
PR = RQ
अत: C पर खींची गई स्पर्श रेखा, P तथा Q पर खींची गई स्पर्श रेखा का समद्विभाजन करती है।

प्रश्न 2.
5 सेमी त्रिज्या वाले एक वृत्त के बिन्दु P पर स्पर्श रेखा PQ केन्द्र 0 से जाने वाली एक रेखा के बिन्दु Q पर इस प्रकार मिलती है कि OQ = 13 सेमी. तो PQ की लम्बाई ज्ञात कीजिए।
हल:
∵ PQ वृत्त पर एक स्पर्श रेखा है। OP वृत्त की त्रिज्या है।

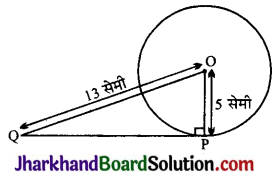
∴ PQ ⊥ OP अर्थात् ∠OPQ = 90°
समकोण त्रिभुज OPQ में, पाइथागोरस प्रमेय से
OQ² = OP² + PQ²
⇒ 13² = 5² + PQ²
⇒ PQ² = 13² – 5²
⇒ PQ² = (13 + 5) (13 – 5)
⇒ PQ² = 18 × 8
⇒ PQ = \(\sqrt{144}\)
⇒ PQ = 12 सेमी.
अतः PQ की लम्बाई = 12 सेमी.।

प्रश्न 3.
सिद्ध कीजिए कि दो संकेन्द्रीय वृत्तों में बड़े वृत्त की जीवा, जो कि छोटे को स्पर्श करती है, स्पर्श बिन्दु पर समद्विभाजित होती है।
हल:
दिया है : माना दो संकेन्द्रीय वृत्त जिनके केन्द्र O और त्रिज्या r और r’ हैं, r > r’
माना AB बड़े वृत्त की जीवा है, जो छोटे वृत्त को C पर स्पर्श करती है।

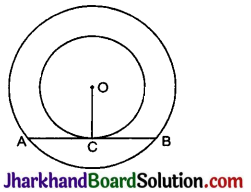
सिद्ध करना है : AC = CB.
रचना: ∵ OC को मिलाया।
उपपत्ति: OC छोटे वृत्त की त्रिज्या है।
और जीवा AB को बिन्दु C पर स्पर्श करती है।
∴ AB, बिन्दु C पर छोटे वृत्त की स्पर्श रेखा है।
∠OCB = 90° (प्रमेय 10.1 से )
अत: AB बड़े वृत्त की जीवा है और OC ⊥ AB,
AC = CB
[∵ वृत्त के केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है]

प्रश्न 4.
O केन्द्र वाले वृत्त के बाह्य बिन्दु P से वृत्त पर दो स्पर्श रेखाएँ PQ और PR खींची गई हैं। सिद्ध कीजिए कि QORP एक चक्रीय चतुर्भुज है।
हल:
हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।

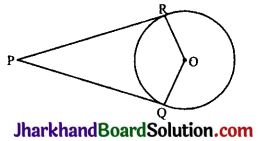
∴ ∠PRO = 90° तथा ∠PQO = 90°
∠PRO + ∠PQO = 90° + 90°
= 180° …..(1)
चतुर्भुज QORP में
∠PRO + ∠ROQ + ∠PQO + ∠QPR = 360°
⇒ ∠PRO + ∠PQO + ∠ROQ + ∠QPR = 360°
⇒ 180° + ∠ROQ + ∠QPR = 360° [समी. (1) से]
⇒ ∠ROQ + ∠QPR = 360° – 180°
⇒ ∠ROQ + ∠OPR = 180°
अतः सम्मुख कोणों का योग 180° है। अतः QORP एक चक्रीय चतुर्भुज है।

प्रश्न 5.
आकृति में, O केन्द्र वाले वृत्त की PQ एक जीवा है तथा PT एक स्पर्श रेखा है। यदि ∠QPT = 60° है, तो ∠PRQ ज्ञात कीजिए।

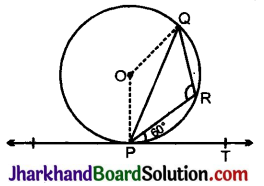
हल:
चित्र से,
OP ⊥ PT अर्थात् OPT = 90°
∠OPQ = ∠OPT – ∠OPT
∠OPQ = 90 – 60
= 30°
ΔOPQ मैं, (वृत्त की त्रिज्या बराबर होती है।)
∠OQP = ∠OPQ = 30°
(बराबर भुजाओं के सम्मुख कोण बराबर होते हैं)
अब,
∠QP + ∠OPQ + ∠POQ = 180°
कोण का योग = 30° + 30° + ∠POQ = 180°
∠POQ = 180° – 60° = 120°
∠POQ = 360° – 120° = 240°
हम जानते हैं, वृत्त के केन्द्र पर बना कोण वृत्त की परिधि पर बने कोण का दुगना होता है।
∠POQ = 2∠PRQ
⇒ 240° = 2∠PRQ
⇒ ∠PRQ = \(\frac{240^{\circ}}{2}\) = 120°
अतः कोण PRQ की माप 120° है।

प्रश्न 6.
सिद्ध करो कि वृत्त की किसी जीवा के सिरों पर खींची गई स्पर्श रेखाएँ, जीवा से समान कोण बनाती हैं।
हल:
माना वृत्त C(O, r) की जीवा AB के सिरे A और B पर स्पर्श रेखाएँ PA और PB खींची गई हैं जो कि बिन्दु P पर काटती हैं।
माना OP, जीवा AB को C बिन्दु पर काटती है।

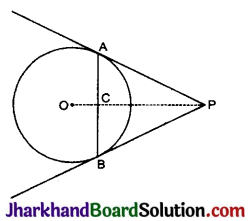
सिद्ध करना है : ∠PAC = ∠PBC
उपपत्ति : ΔPCA और ΔPCB में,
PA = PB (बाह्य बिन्दु P से वृत्त पर स्पर्श रेखाएँ हैं)
PC = PC (उभयनिष्ठ भुजा)
∠APC = ∠BPC [∵ स्पर्श रेखाएँ PA व PB, OP के साथ समान कोण बनाती हैं]
S-A-S सर्वांगसमता से,
ΔPCA ≅ ΔPCB
⇒ ∠PAC = ∠PBC.

प्रश्न 7.
आकृति में, 3 सेमी. त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD तथा DC की लम्बाइयाँ क्रमशः 6 सेमी तथा 9 सेमी है। यदि ΔABC का क्षेत्रफल 54 वर्ग सेमी है, तो भुजाओं AB तथा AC की लम्बाइयाँ ज्ञात कीजिए।

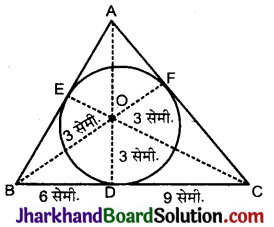
हल:
3 सेमी त्रिज्या वाले वृत्त के परिगत एक ΔABC खींचा गया है। त्रिभुज की भुजाएँ BC, AB, AC वृत्त को क्रमश: D, E, F बिन्दुओं पर स्पर्श करती है।
∵ किसी बाह्य बिन्दु से, वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई समान होती हैं।
AE = AF = x (माना)
BD = BE = 6 सेमी
CD = CF = 9 सेमी
OF, OE, OA, OB तथा OC को मिलाया।
हम जानते हैं कि वृत्त की स्पर्श रेखा बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।
∴ OD ⊥ BC, OE ⊥ AB, OF ⊥ AC
ΔABC में, b = AB = (x + 6)
a = BC = (6 + 9) = 15 सेमी
c = AC = (x + 9) सेमी

ΔOCB का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × 15 × 3 = \(\frac{45}{2}\) सेमी²
ΔCOA का क्षेत्रफल = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (x + 9) × 3
= \(\frac{3 x+27}{2}\) सेमी²
ΔAOB का क्षे. = \(\frac{1}{2}\) × आधार × शीर्षलम्ब
= \(\frac{1}{2}\) × (6 + x)³ = \(\frac{18+3 x}{2}\) सेमी²
ΔABC का क्षे. = ΔOCB का क्षे. + ΔCOA का क्षे + ΔAOB का क्षे.
\(\sqrt{54 x^2+810 x}=\frac{45}{2}+\frac{3 x+27}{2}+\frac{18+3 x}{2}\)
= \(2 \sqrt{54 x^2+810 x}\) = 45 + 3x + 27 + 18 + 3x
वर्ग करने पर,
4(54x² + 810x) = (6x + 90)²
54 × 4(x² + 15x) = 36(x + 15)²
6x(x + 15) = (x + 15)²
6x = x + 15
5x = 15
x = 3
AE = AF = 3 सेमी
∴ AB = AE + EB = 3 + 6 = 9 सेमी
AC = AF + FC = 3 + 9 = 12 सेमी

प्रश्न 8.
दी गई आकृति में, त्रिभुज ABC की भुजाएँ AB, BC तथा CA, केन्द्र O तथा त्रिज्या r वाले वृत्त को क्रमश: P, Q तथा R पर स्पर्श करती हैं।

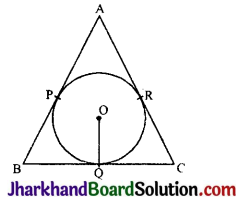
सिद्ध कीजिए :
(i) AB + CQ = AC + BQ
(ii) क्षेत्रफल (ΔABC) = \(\frac{1}{2}\)(ΔABC का परिमाप) × r
हल:
(i) चूँकि हम जानते हैं कि बाह्य वृत्त से खींची गई स्पर्श रेखाएँ बराबर होती हैं।
अतः AP = AR …..(1)
(बिन्दु A से वृत्त पर खींची गई स्पर्श रेखाएँ)
BP = BQ …..(2)
(बिन्दु B से वृत्त पर खींची गई स्पर्श रेखाएँ)
तथा CQ = CR …..(3)
(बिन्दु C से वृत्त पर खींची गई स्पर्श रेखाएँ)
समी. (1), (2) तथा (3) को जोड़ने पर
AP + BP + CQ = AR + BQ + CR
⇒ (AP + BP) + CQ = (AR + CR) + BQ
⇒ AB + CQ = AC + BQ.

(ii) OR, OP, OA, OB तथा OC को मिलाया।
चूँकि हम जानते हैं कि स्पर्श रेखा स्पर्श बिन्दु से होकर खींची गई त्रिज्या पर लम्ब होती है।

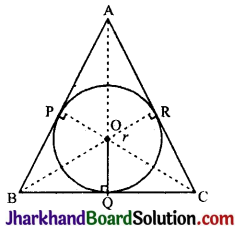
अत: OP ⊥ AB, OQ ⊥ BC तथा OR ⊥ AC
अब (ΔABC) का क्षेत्रफल = त्रिभुज BOC का क्षेत्रफल + त्रिभुज AOC का क्षेत्रफल + त्रिभुज AOB का क्षेत्रफल
= \(\frac{1}{2}\)BC × OQ + \(\frac{1}{2}\) AC × OR + \(\frac{1}{2}\)AB × OP
(∵ त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\)आधार × ऊँचाई)
= \(\frac{1}{2}\)(BC × r + AC × r + AB × r)
(∵ OQ, OR तथा OP वृत्त की त्रिज्याएँ हैं)
= \(\frac{1}{2}\)(BC + AC + AB) × r
= \(\frac{1}{2}\)(ΔABC का परिमाप) × r
अत: ΔABC का क्षेत्रफल = \(\frac{1}{2}\)(ΔABC का परिमाप) × r

प्रश्न 9.
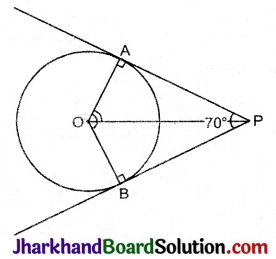
यदि एक बिन्दु T से O केन्द्र वाले किसी वृत्त पर TA व TB स्पर्श रेखाएँ परस्पर 70° के कोण पर झुकी हों तो ∠AOB को ज्ञात कीजिए।
हल:
बिन्दु T से TA व TB वृत्त की दो स्पर्श रेखाएँ है। OA तथा OB वृत्त की त्रिज्याएँ है।

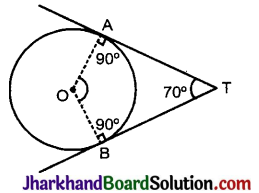
अत: AT ⊥ OA तथा BT ⊥ OB (प्रमेय 10.1 से)
∴ ∠OAT = 90°
तथा ∠OBT = 90°
∠AOB + ∠ATB = 180°
∠AOB + 70° = 180°
∠AOB = 180° – 70° = 110°

प्रश्न 10.
निम्न आकृति में XP तथा XQ, केन्द्र O वृत्त पर बिन्दु X से खींची गई स्पर्श रेखाएँ हैं तथा AB वृत्त के बिंदु R पर स्पर्श रेखा है।
सिद्ध कीजिए : XA + AR = XB + BR

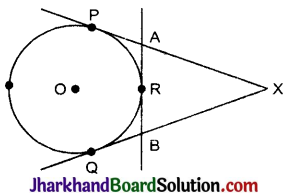
हल:
∵ वृत्त के किसी बाह्य बिन्दु से खींची गई स्पर्श रेखाएँ बराबर होती है।
∴ XP = XQ
⇒ XA + AP = XB + BQ …..(i)
बिन्दु B से खींची गई स्पर्श रेखाएँ BQ तथा BR है।
∴ BQ = BR …..(ii)
इसी प्रकार AP = AR ……(iii)
समीकरण (i), (ii) व (iii) से
XA + AR = XB + BR

प्रश्न 11.
एक त्रिभुज ABC के अन्तर्गत एक वृत्त इस प्रकार खींचा गया है कि यह भुजाओं AB, BC तथा AC को क्रमश: P, Q तथा R पर स्पर्श करता है, यदि AB = 10 सेमी, AR = 7 सेमी तथा CR = 5 सेमी है, तो BC की लम्बाई ज्ञात कीजिए।
हल:
दिया है, AB = 10 सेमी
AR = 7 सेमी
तथा CR = 5 सेमी

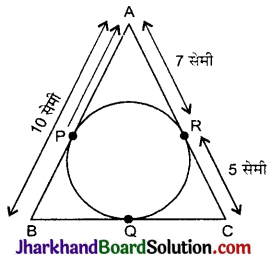
∵ बिन्दु A से दो स्पर्श रेखाएँ खींची गई हैं।
∴ AP = AR = 7 सेमी
∵ AB = AP + PB
⇒ 10 = 7 + PB
⇒ PB = (10 – 7) सेमी = 3 सेमी
बिन्दु B से खींची गई स्पर्श रेखाएँ BP व BQ बराबर हैं।
∴ BQ = BP = 3 सेमी
तथा बिन्दु C से खींची गई स्पर्श रेखाएँ CQ व CR बराबर हैं।
CQ = CR = 5 सेमी
अतः BC = BQ + QC
= 3 सेमी + 5 सेमी
= 8 सेमी

प्रश्न 12.
निम्न आकृति में O केंन्द्र वाले वृत्त का व्यास AB है तथा AC इसकी एक जीवा है। ∠BAC = 30° है। यदि बिंदु C पर खींची गई स्पर्श रेखा, बढ़ाए गए व्यास AB को बिन्दु D पर प्रतिच्छेद करती है, तो दर्शाइए कि BC = BD।

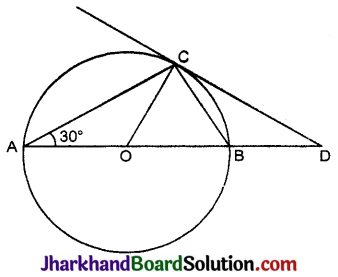
हल:
अर्धवृत्त में स्थित कोण समकोण होता है,
∠ACB = 90°
ΔABC में,
∠ABC + ∠ACB + ∠OAB = 180°
⇒ ∠ABC + 90° + 30° = 180°
⇒ ∠ABC = 180° – 120° = 60°
∠ABC + CBD = 180° (रैखिक युग्म)
⇒ 60° + ∠CBD = 180°
⇒ ∠CBD = 180° – 60°- 120°
ΔAOC में
OA = OC
⇒ ∠ACO = ∠OAC = 30°
अब ∠ACB = ∠ACO + ∠OCB
⇒ 90° = 30° + ∠OCB
⇒ ∠OCB = 90° – 30° = 60°
∵ स्पर्श रेखा, त्रिज्या पर लम्ब होती है।
∴ ∠ACD = 90°
⇒ ∠OCB + ∠BCD = 90°
⇒ 60° + ∠BCD = 90°
⇒ ∠BCD = 90° – 60° = 30°
ΔCBD में,
∠BCD + ∠CBD + ∠BDC = 180°
⇒ 30° + 120° + BDC = 180°
⇒ ∠BDC = 180° – 150° = 30°
∵ ∠BCD = ∠BDC = 30°
⇒ BD = BC

वस्तुनिष्ठ प्रश्न :

रिक्त स्थानों की पूर्ति कीजिए :

प्रश्न (क).

1. दो वृत्त एक-दूसरे को ………………. बिन्दु पर प्रतिच्छेद करते हैं।
2. वृत्त के बाहर स्थित बिन्दु से वृत्त पर ………………. स्पर्श रेखाएँ खींची जा सकती है।
3. वह रेखा जो वृत्त को दो बिन्दुओं पर काटती है ………………. कहलाती है।
4. त्रिभुज का अन्तः वृत्त ………………. का प्रतिच्छेदक बिन्दु होता है।
5. वृत्त के बाहरी बिन्दु P से वृत्त पर स्पर्श रेखा, केन्द्र O से हमेशा OP से ………………… होती है।

उत्तर:

1. दो,
2. 2,
3. छेदक रेखा,
4. त्रिभुज के कोणों का समद्विभाजक,
5. कम ।

निम्न में सत्य / असत्य ज्ञात कीजिए :

प्रश्न (ख).

1. वृत्त की दो स्पर्श रेखाओं की लम्बाई समान होती है।
2. किसी वृत्त पर खींची गई छेदक रेखा वृत्त को दो बिन्दुओं पर प्रतिच्छेद करती है।
3. समद्विबाहु त्रिभुज ABC के परिगत वृत्त पर बिन्दु से स्पर्श रेखाएँ इस प्रकार हैं कि AB = AC जो BC के समान्तर है।
4. वृत्त के बाहर स्थित किसी बिन्दु से वृत्त पर अनेक स्पर्श रेखाएँ खींची जा सकती हैं।
5. स्पर्श रेखा और वृत्त के उभयनिष्ठ बिन्दु को स्पर्श बिन्दु कहते हैं।

उत्तर:

1. सत्य,
2. सत्य,
3. सत्य,
4. असत्य,
5. सत्य ।

(ग) बहुविकल्पीय प्रश्न :

प्रश्न 1.
निम्न आकृति में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 115° है, तो ∠PTQ बराबर है:

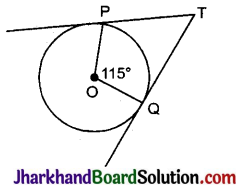
(A) 115°
(B) 57.5°
(C) 55°
(D) 65°
हल:
∵ ∠PTO और ∠POQ सम्पूरक कोण हैं।
∠PTQ + ∠POQ = 180°
⇒ ∠PTQ + 115° = 180°
⇒ ∠PTQ = 180° – 115° = 650
अत: सही विकल्प (D) है।

प्रश्न 2.
निम्न आकृति में, O केन्द्र वाले वृत्त पर बिन्दु B पर स्पर्श रेखा PQ खींची गई है। यदि ∠AOB = 100° है, तो ∠ABP बराबर है :

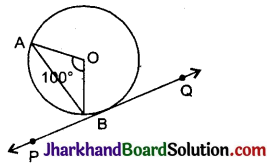
(A) 50°
(B) 40°
(C) 60°
(D) 80°
हल:
दिया है,
∠AOB = 100°
∵ OA = OB
⇒ ∠OBA = ∠OAB = \(\frac{180^{\circ}-100^{\circ}}{2}\)
⇒ ∠OBA = ∠OAB = 40°
∵ स्पर्श रेखा त्रिज्या पर लम्ब होती है।
∴ ∠OBP = 90°
∴ ∠ABP + ∠ABO = 90°
⇒ ∠ABP + 40° = 90°
⇒ ∠ABP = 90° – 40° = 50°
अत: सही विकल्प (A) है।

प्रश्न 3.
निम्न आकृति में, O केन्द्र वाले वृत्त पर बाहय बिंदु P से दो स्पर्श रेखाएँ PQ तथा PR खींची गई हैं। वृत्त की त्रिज्या 4 सेमी है। यदि ∠QPR = 90° है, तो PQ की लम्बाई होगी:

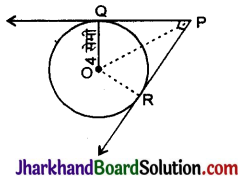
(A) 3 सेमी
(B) 4 सेमी
(C) 2 सेमी
(D) 2\(\sqrt{2}\) सेमी
हल:
∵ त्रिज्या, स्पर्श रेखा पर लम्ब होती है,
∠OQP = ∠ORP = 90°
दिया है, ∠QPR = 90°
चतुर्भुज PQOR में,
∠PQO+ ∠QOR + ∠ORP + ∠RPQ = 360°
⇒ 90° + ∠QOR + 90° + 90° = 360°
⇒ ∠QOR = 360°- 270° = 90°
∴ PR = PQ
⇒ ∠POQ = ∠POR = \(\frac{90^{\circ}}{2}\) = 45°
समकोण ΔOQP में,
tan 45° = \(\frac{P Q}{O Q}\)
⇒ 1 = \(\frac{P Q}{4}\)
⇒ PQ = 4 सेमी
अत: सही विकल्प (B) है।

प्रश्न 4.
निम्न चित्र में 7 सेमी त्रिज्या के एक वृत्त के बाहय बिंदु P से स्पर्श रेखा PT खींची गई है कि PT = 24 सेमी है। यदि O वृत्त का केन्द्र है, तो PR की लंबाई है:

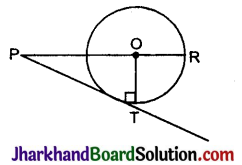
(A) 30 सेमी
(B) 28 सेमी
(C) 32 सेमी
(D) 25 सेमी
हल:
समकोण ΔPTO में,
OP² = OT² + PT²
⇒ OP² = (7)² + (24)²
⇒ Op² = 49 + 576 = 625
⇒ OP = 25 सेमी
∴ PR = PO + OR
= (25 + 7) सेमी
= 32 सेमी
अतः सही विकल्प (C) है।

प्रश्न 5.
निम्न आकृति में, O वृत्त का केन्द्र है। PQ एक जीवा है तथा PT, P पर एक स्पर्श रेखा है, जो PQ के साथ 50° का कोण बनाती है। ∠POQ का मान है:

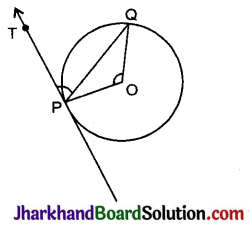
(A) 130°
(B) 90°
(C) 100°
(D) 75°
हल:
∵ त्रिज्या स्पर्श रेखा पर लम्ब होती है।
∴ ∠OPT = 90°
∴ ∠OPQ + ∠QPT = 90°
⇒ ∠OPQ = 90° – 50° = 40°
∵ OP = OQ
⇒ ∠OQP = ∠OPQ = 40°
ΔPOQ में,
∠OQP + ∠OPQ + ∠POQ = 180°
⇒ 40° + 40° + ∠POQ = 180°
⇒ ∠POQ = 180° – 80° = 100°
अत: सही विकल्प (C) है।

प्रश्न 6.
एक वृत्त के केन्द्र से 13 सेमी दूरी पर स्थित एक बिन्दु Q से वृत्त पर खींची गई स्पर्श रेखा PQ की लम्बाई 12 सेमी है। वृत्त की त्रिज्या (सेमी. में) है:
(A) 25
(B) \(\sqrt{313}\)
(C) 5
(D) 1
हल:
बाह्य बिन्दु Q से PQ वृत्त पर खींची गई स्पर्श रेखा है तथा OP वृत्त की त्रिज्या है।

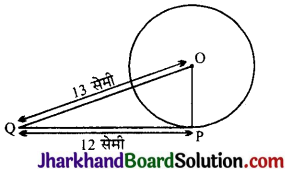
अतः ∠OPQ = 90° (प्रमेय 10.1 से)
समकोण त्रिभुज OPQ में,
OQ² = PQ² + OP² (पाइथागोरस प्रमेय से)
⇒ 13² = 12² + OP²
⇒ OP² = 13² – 12²
⇒ OP² = (13 + 12) (13 – 12)
⇒ OP² = 25
⇒ OP = \(\sqrt{25}\) = 5 सेमी.
अत: विकल्प (C) सही है।

प्रश्न 7.
दी गई आकृति में AP, AQ तथा BC वृत्त की स्पर्श रेखाएँ हैं। यदि AB = 5 सेमी., AC = 6 सेमी. तथा BC = 4 सेमी है, तो AP की लम्बाई (सेमी. में) है:

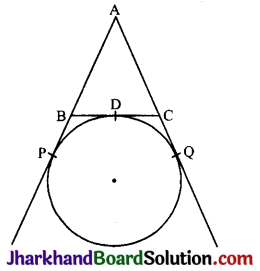
(A) 7.5
(B) 15
(C) 10
(D) 9
हल चूँकि हम जानते हैं कि बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
अत: BP = BD …..(1)
(बिन्दु B से वृत्त पर स्पर्श रेखाएँ)
CQ = CD …..(2)
(बिन्दु C से वृत्त पर स्पर्श रेखाएँ)
AP = AQ …..(3)
(बिन्दु A से वृत्त पर स्पर्श रेखाएँ) अब
AP = AB + BP ⇒ AP = 5 + BD ….. (4)
AQ = AC + CQ ⇒ AQ = 6 + CD ….. (5)
समी (4) तथा (5) को जोड़ने पर,
AP + AQ = 5 + BD + 6 + CD
⇒ AP + AP = 11 + BD + CD
[समी. (3) का प्रयोग करने पर]
⇒ 2AP = 11 + BC
⇒ 2AP = 11 + 4
⇒ 2AP = 15 ⇒ AP = 7.5 सेमी.
अत: विकल्प (A) सही है।

प्रश्न 8.
यदि एक बाह्य बिन्दु P से एक O केन्द्र वाले वृत्त पर दो स्पर्श रेखाएँ PA और PB इस प्रकार खीची गई कि दोनों 80° के कोण पर झुकी है, तो ∠POA बराबर हैं:
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल:
बिन्दु P से PA तथा PB वृत्त पर स्पर्श रेखाएँ हैं तथा OA व OB वृत्त की त्रिज्याएँ हैं।
अत: AP ⊥ OA तथा PB ⊥ OB (प्रमेय 10.1 से)

∠OAP = 90°
तथा ∠OBP = 90°
अब ∠AOB + ∠APB = 180°
⇒ ∠AOB + 70° = 180°
⇒ ∠AOB = 180° – 80°
∴ ∠AOB = 100°
∵ OP रेखा, ∠AOB का समद्विभाजक है।
∠POA = \(\frac{\angle A O B}{2}=\frac{100^{\circ}}{2}\) = 50°
∴ ∠POA = 50°
अत: सही विकल्प (A) है।

प्रश्न 9.
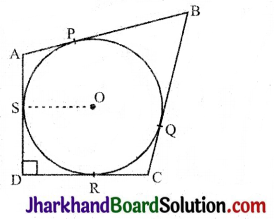
दी गई आकृति में, एक चतुर्भुज ABCD के अन्तर्गत खींचा गया वृत्त, इसकी भुजाओं AB, BC, CD तथा AD को क्रमश: P, Q, R तथा S पर स्पर्श करता है। यदि वृत्त की त्रिज्या 10 सेमी., BC = 38 सेमी. PB = 27 सेमी. तथा AD ⊥ CD है, तो CD की लम्बाई है:

(A) 11 सेमी
(B) 20 सेमी
(C) 21 सेमी
(D) 15 सेमी
हल:
बिन्दु D से DR तथा DS वृत्त पर स्पर्श रेखाएँ हैं तथा OS व OR वृत्त की त्रिज्याएँ है।

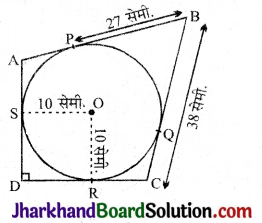
AD⊥ OS तथा DR ⊥ OR (प्रमेय 10.1 से)
AD ⊥ CD (दिया है)
चतुर्भुज DROS में,
∠D + ∠R + ∠O + ∠S = 360°
⇒ 90° + 90° + ∠O + 90° = 360°
⇒ ∠O = 360° – 270° = 90°
इस प्रकार चतुर्भुज DROS में,
∠D = ∠R = ∠O = ∠S = 90°
तथा OS = OR [एक ही वृत्त की त्रिज्याएँ]
अत: DROS एक वर्ग होगा।
अतः SD = DR = 10 सेमी
(बिन्दु D से वृत्त पर स्पर्श रेखाएँ)
∵ बिन्दु B से BP व BQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ BP = BQ = 27 सेमी (प्रमेय 10.2 से)
CQ = BC – BQ
CQ = 38 – 27 = 11 सेमी
∵ बिन्दु C से CR व CQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ CR = CQ (प्रमेय 10.2 से)
⇒ CR = 11 सेमी
CD = CR + DR
⇒ CD = 11 + 19
⇒ CD = 21 सेमी
अत: विकल्प (C) सही है।

प्रश्न 10.
किसी 5 सेमी. त्रिज्या वाले वृत्त के एक व्यास AB के पर स्पर्श रेखा XAY खींची गई है। XY के समान्तर 4 से 8 सेमी की दूरी पर, जीवा CD की लम्बाई है:
(A) 4 सेमी
(B) 5 सेमी
(C) 6 सेमी
(D) 8 सेमी
हल:
चूँकि X-AY वृत्त पर स्पर्श रेखा है तथा OA व OC वृत्त की त्रिज्याएँ हैं।

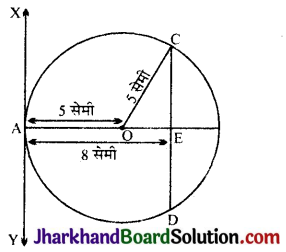
अत: XY ⊥ OA अर्थात् ∠XAO = 90° (प्रमेश 10.1 से)
∵ XY || CD (दिया गया है)
∴ ∠XAO + ∠OEC = 180°
⇒ 90° + ∠OEC = 180°
⇒ ∠OEC = 180° – 90° = 90°
AE = 8 सेमी
तथा AO = 5 सेमी (वृत्त की त्रिज्या)
∴ OE = AE – AO
= 8 – 5 = 3 सेमी
समकोण त्रिभुज OEC में,
OC² = OE² + CE² (पाइथागोरस प्रमेय)
⇒ 5² = 3² + CE²
⇒ CE² = 5² – 3²
= 25 – 9 = 16
⇒ CE = \(\sqrt{16}\) = 4 सेमी
OE ⊥ CD
CE = ED
CD = 2 × CE = 2 × 4 = 8 सेमी
अतः विकल्प (D) सही है।

प्रश्न 11.
यदि 60° पर झुकी दो स्पर्श रेखाएँ 3 सेमी त्रिज्या वाले एक वृत्त पर खींची जाती हैं, तो प्रत्येक स्पर्श रेखा की लम्बाई है:
(A) 3 सेमी
(B) \(\frac{3}{2} \sqrt{3}\) सेमी
(C) 3\(\sqrt{3}\) सेमी
(D) 6 सेमी
हल:
माना बिन्दु P से PQ तथा PR वृत्त पर स्पर्श रेखाएँ हैं। OQ तथा OR वृत्त की त्रिज्याएँ हैं।

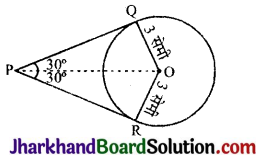
अतः PQ ⊥ OQ तथा PR ⊥ OR
अतः समकोण ΔPOQ तथा ΔPOR में
∠OQP = ∠ORP (प्रत्येक 90° है)
कर्ण PO = कर्ण PO (उभयनिष्ठ भुजा)
तथा OQ = OR (वृत्त की समान त्रिज्याएँ)
∴ ΔPOQ ≅ ΔPOR (समकोण कर्ण भुजा सर्वांगसमता गुणधर्म से)
⇒ ∠QPO = ∠RPO (CPCT)
⇒ ∠QPO = ∠RPO
= \(\frac{60^{\circ}}{2}\) = 30°
अब समकोण ΔOQP में
tan 30° = \(\frac{O Q}{P Q}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{3}{P Q}\)
⇒ PQ = 3\(\sqrt{3}\)
चूँकि बिन्दु P से PQ तथा PR वृत्त पर खींची गई स्पर्श रेखाएँ हैं और हम जानते हैं कि वृत्त पर बाह्य बिन्दु से खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती है।
अत: PR = PQ
= 3\(\sqrt{3}\) सेमी.
अतः विकल्प (C) सही है।